一些可爱的最值（DP 优化小总结）

简单区间最值

\[f_i=\min\limits_{j\in[L_i,R_i]}\{f_j+w_j\}+c_i \]

若 $L_i\leq L_{i+1},R_i\leq R_{i+1}$，即滑动窗口：
单调队列 $\mathcal{O}(n)$ 解决。
否则：
单点修改、区间最值查询，上数据结构，用树状数组或线段树或平衡树 $\mathcal{O}(n\log n)$ 解决。
或者 CDQ 分治，对左侧建出 ST 表查询，做到整体 $\mathcal{O}(n\log^2n)$，或者用 $\mathcal{O}(n)\sim\mathcal{O}(1)$ 的区间最值查询，做到 $\mathcal{O}(n\log n)$。

斜率优化

一句话概括，线性规划，进而发现可能产生贡献的点都在凸包上，于是只用维护上 / 下凸包，每次查询的时候切凸包。

小问题

对于所有 $i$，求：

\[\min_{j\lt i}\frac{Y_i-Y_j}{X_i-X_j} \]

就是过 $(X_j,Y_j),(X_i,Y_i)$ 斜率最小值。对于所有 $j\lt i$，建出上凸包，每次 $\mathcal{O}(\log n)$ 二分凸包找切线。

若 $X$ 单增，直接单调栈维护凸包。整体 $\mathcal{O}(n\log n)$。

否则，可以分块，设块长为 $B$，单点修改需要 $\mathcal{O}(B)$ 重建凸包，查询的时候对于每个凸包二分，$\mathcal{O}(\frac{n}{B}\log B)$，取 $B=\sqrt{n\log n}$，则总体做到 $\mathcal{O}(n\sqrt{n\log n})$。

或者，可以平衡树维护凸包，做到 $\mathcal{O}(n\log n)$。

或者，可以 CDQ 分治，对 $X$ 归并排序，就能线性建立凸包，但是瓶颈在于二分凸包，整体还是 $\mathcal{O}(n\log^2n)$。

HDU - 2993 可以练练手，由于 $X,Y$ 都是单调的，所以线性维护凸包，双指针找切点，做到 $\mathcal{O}(n)$。

更常见的形式

\[f_i=\min_{j\lt i}\{e_i\cdot f_j+a_j+b_j\cdot c_i\}+d_i \]

即 $f_i=A[i]A[j]+[j]$ 或 $f_i=A[i]A[j]+B[i]B[j]$。

化成：

\[Y_j=k_i\cdot X_j+b_i \]

的形式，其中 $f_i$ 包含在 $b_i$ 中，于是只需要维护 $(X_j,Y_j)$ 的凸包，根据 $\min/\max$ 分别维护下 / 上凸包。

不妨设求 $\min$，维护下凸包。

若 $X$ 单增
可以单调栈线性维护凸包。
1. 若 $k_i$ 单增
  双指针找切点，总时间 $\mathcal{O}(n)$。
2. $k_i$ 无单调性
  二分凸包，总时间 $\mathcal{O}(n\log n)$。
$X$ 无单调性
类似小问题中的分析，可以分块、平衡树、CDQ。当然 CDQ 最好写了，时间挺优秀的，若 $k_i$ 单增可以做到 $\mathcal{O}(n\log n)$，否则需要二分凸包 $\mathcal{O}(n\log^2n)$。

写法容易被 Hack

为了避免浮点数误差，$\frac{y_c-y_a}{x_c-x_a}\leq\frac{y_b-y_a}{x_b-x_a}$ 移项后变为 $(y_c-y_a)(x_b-x_a)\leq(y_b-y_a)(x_c-x_a)$，记住有可能会爆 long long，要使用 __int128 比较。同时，这里不变号的前提是保证了 $x$ 是有序的，$x_a\leq x_b\leq x_c$ 或 $x_a\geq x_b\geq x_c$。

但是这样写还是错的。

bool cmptail(int a, int b, int c) {
    return (i128(Y(c) - Y(a))) * (X(b) - X(a)) <= (i128(Y(b) - Y(a))) * (X(c) - X(a));
}

在这题 [CEOI 2017] Building Bridges 中，就被卡掉了。拍出了一组很小的数据：

5
3 3 3 3 2
-7 1 -1 6 9

其中，$y_i=f_i+h_i^2-w_i$，$x_i=2h_i$，前三个点的坐标是：

1: (6, 16)
2: (6, 15)
3: (6, 16)

显然，凸包应该为 $\{1,2,3\}$，但是上述代码会把 2 pop 掉。所以需要加上 x 相等时的特判：

bool cmptail(int a, int b, int c) {
    if (X(b) == X(c))
        return Y(c) <= Y(b);
    return (i128(Y(c) - Y(a))) * (X(b) - X(a)) <= (i128(Y(b) - Y(a))) * (X(c) - X(a));
}

有同学会问，不加特判，而是把 $\leq$ 改成 $\lt$ 可以吗？这样也是错的，考虑另一组很小的数据：

5
2 2 2 2 2
8 -8 7 -5 -10

前三个点的坐标为：

1: (4, -4)
2: (4, 4)
3: (4, -11)

显然，凸包应为 $\{1,3\}$，而将 $\leq$ 改成 $\lt$ 就得到了 $\{1,2,3\}$ 的错误结果。所以，只有加上特判的那一种写法是对的。

LCT（LiChaoTree）

\[Y_i=k_jX_i+b_j \]

$f_i$ 包含在 $Y_i$ 中。只需要维护所有 $j$ 对应的直线，用李超树单点查询即可。

决策单调性

决策单调性和是否能够斜率优化没有直接关系，可以视作并列关系。当 $X$ 单增、$k_i$ 单增的时候，确实是决策单调的。

小问题

对于所有 $i$，求：

\[\min_{j\lt i}w(j,i) \]

推荐打表找规律，最优转移点 $j$ 是否随着 $i$ 增加而单增，若是，则满足决策单调性。

四边形不等式提供了决策单调性的一个充分不必要条件，即若对于 $a\leq b\leq c\leq d$，均有 $w(a,c)+w(b,d)\leq w(a,d)+w(b,c)$。

分治
记录求解区间 $[l,r]$ 和决策区间 $[l_k,r_k]$。由于递归树每一层都有 $\bigcup[l_k,r_k]=[1,n]$，所以时间复杂度为 $\mathcal{O}(n\log n)$。

int w(int j, int i);

void DP(int l, int r, int k_l, int k_r) {
  int mid = (l + r) / 2, k = k_l;
  // 求状态 f[mid] 的最优决策点
  for (int j = k_l; j <= min(k_r, mid - 1); ++j)
    if (w(j, mid) < w(k, mid)) k = j;
  f[mid] = w(k, mid);
  // 根据决策单调性得出左右两部分的决策区间，递归处理
  if (l < mid) DP(l, mid - 1, k_l, k);
  if (r > mid) DP(mid + 1, r, k, k_r);
}

队列
维护可能成为最优转移点的队列。

需要实现一个函数 $\operatorname{get}(j,i)$（$j\lt i$），表示当 $t\ge\operatorname{get}(j,i)$ 时，$i\rightarrow t$ 优于 $j\rightarrow t$，即 $w(i,t)\lt w(j,t)$，当不存在的时候返回 $n+1$。而这个是可以通过二分实现的。注意这里严格小于和小于等于有区别，在后文说明。

每次先把队头弹掉，可以通过比较 $w(q_{\mathtt{head}},i)$ 和 $w(q_{\mathtt{head}+1},i)$，也可以比较 $\operatorname{get}(q_{\mathtt{head}},q_{\mathtt{head}+1})$ 和 $i$ 的关系。

这样操作后，$q_\mathtt{head}$ 就是 $i$ 的最优转移点。

然后往队列里尝试插入 $i$。若 $\operatorname{get}(q_{\mathtt{tail}-1},q_{\mathtt{tail}})\geq\operatorname{get}(q_{\mathtt{tail}},i)$：

$\operatorname{get}(q_{\mathtt{tail}-1},q_{\mathtt{tail}})\geq\operatorname{get}(q_{\mathtt{tail}},i)$

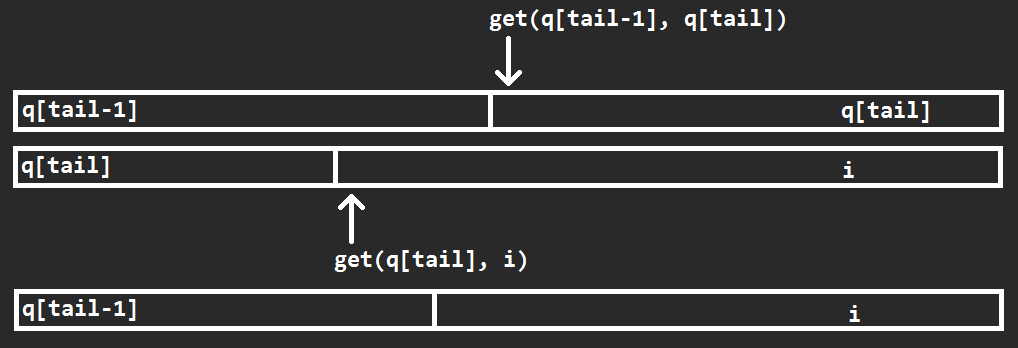
那么 $q_{\mathtt{tail}}$ 没用了，可以弹出，否则 $\operatorname{get}(q_{\mathtt{tail}-1},q_{\mathtt{tail}})\lt\operatorname{get}(q_{\mathtt{tail}},i)$：

$\operatorname{get}(q_{\mathtt{tail}-1},q_{\mathtt{tail}})\lt\operatorname{get}(q_{\mathtt{tail}},i)$

说明 $q_{\mathtt{tail}}$ 在 $\Big[\operatorname{get}(q_{\mathtt{tail}-1},q_{\mathtt{tail}}),\operatorname{get}(q_{\mathtt{tail}},i)\Big)$ 还有用。

由于 $\operatorname{get}()$ 的实现基于二分，所以时间复杂度为 $\mathcal{O}(n\log n)$。

$\operatorname{get}()$ 内部严格小于和小于等于的区别

当你在判断队首时，注意需要取等，否则如果队列前两个相等，而第三个是最后转移点，不把第一个队首弹掉就不知道后面有更优的。所以为了保证队列中不出现这种相等的情况，$\operatorname{get}()$ 内部只能用严格小于判断。当然，在弹队首的时候用 $\operatorname{get}()$（取等）也行。

为什么不能直接双指针？

注意，决策单调性并不意味着 $w(j,i)$ 在 $i$ 固定时随 $j$ 增加而单调，有可能出现 $5,100,3$ 这种情况，要用双指针除非你能快速查询 $w(j,i)$ 的后缀最值，那我都能快速查询后缀最值了，为什么不直接去解决原问题呢？

更常见的形式

\[f_i=\min_{j\lt i}\Big\{f_j+w(j,i)\Big\} \]

同样，$w(j,i)$ 满足四边形不等式是决策单调性的一个充分不必要条件。

可以直接通过队列方式维护了。时间复杂度 $\mathcal{O}(n\log n)$。

但是直接分治是不好做的，因为有依赖条件，那么用 CDQ 套一下就可以了，时间复杂度 $\mathcal{O}(n\log^2n)$。

更常见的形式

\[f_{l,r}=\min_{k\in[l,r)}\Big\{f_{l,k}+f_{k+1,r}\Big\}+w(l,r) \]

初值 $f(i,i)=w(i,i)$。

若对于 $[l_1,r_1]\subseteq[l_2,r_2]$，有 $w(l_1,r_1)\leq w(l_2,r_2)$，则其满足区间包含不等式。若其还满足四边形不等式，那么 $f(l,r)$ 也满足四边形不等式。那么最优决策点满足 $\operatorname{opt}(l,r-1)\leq\operatorname{opt}(l,r)\leq\operatorname{opt}(l+1,r)$。

于是可以将 $k$ 的枚举范围变为 $\Big[\operatorname{opt}(l,r-1),\operatorname{opt}(l+1,r)\Big]$，时间复杂度 $\mathcal{O}(n^2)$。

posted @ 2025-07-11 14:14 XuYueming 阅读(85) 评论(0) 收藏举报

刷新页面返回顶部

XuYueming

一些可爱的最值（DP 优化小总结）

简单区间最值

斜率优化

小问题

更常见的形式

写法容易被 Hack

LCT（LiChaoTree）

决策单调性

小问题

更常见的形式

更常见的形式

公告