DirectX11 With Windows SDK--25 法线贴图
前言
注意:这一章对应项目代码2.x.x版本,持有低版本项目代码的同学请到Github更新一份
在很早之前的纹理映射中,纹理存放的元素是像素的颜色,通过纹理坐标映射到目标像素以获取其颜色。但是我们的法向量依然只是定义在顶点上,对于三角形面内一点的法向量,也只是通过比较简单的插值法计算出相应的法向量值。这对平整的表面比较有用,但无法表现出内部粗糙的表面。在这一章,你将了解如何获取更高精度的法向量以描述一个粗糙平面。
DirectX11 With Windows SDK完整目录
欢迎加入QQ群: 727623616 可以一起探讨DX11,以及有什么问题也可以在这里汇报。
法线贴图
法线贴图是指纹理中实际存放的元素通常是经过压缩后的法向量,用于表现一个表面凹凸不平的特性,它是凹凸贴图的一种实现方式。
开启法线贴图后的效果

关闭法线贴图后的效果

法线贴图中存放的法向量\((x, y, z)\)分别对应原来的\((r, g, b)\)。每个像素都存放了对应的一个法向量,经过压缩后使用24 bit即可表示。实际情况则是一张法线贴图里面的每个像素使用了32 bit来表示,剩余的8 bit(位于Alpha值)要么可以不使用,要么用来表示高度值或者镜面系数。而未经压缩的法线贴图通常为每个像素存放4个浮点数,即用128 bit来表示。
下面展示了一张法线贴图,每个像素点位置存放了任意方向的法向量。可以看到这里为法线贴图建立了一个TBN坐标系(左手坐标系),其中T轴(Tangent Axis)对应原来的x轴,B轴(Binormal Axis)对应原来的y轴,N轴(Normal Axis)对应原来的z轴。建立坐标系的目的在后面再详细描述。观察这些法向量,它们都有一个共同的特点,就是都朝着N轴的正方向散射,这样使得大多数法向量的z分量是最大的。
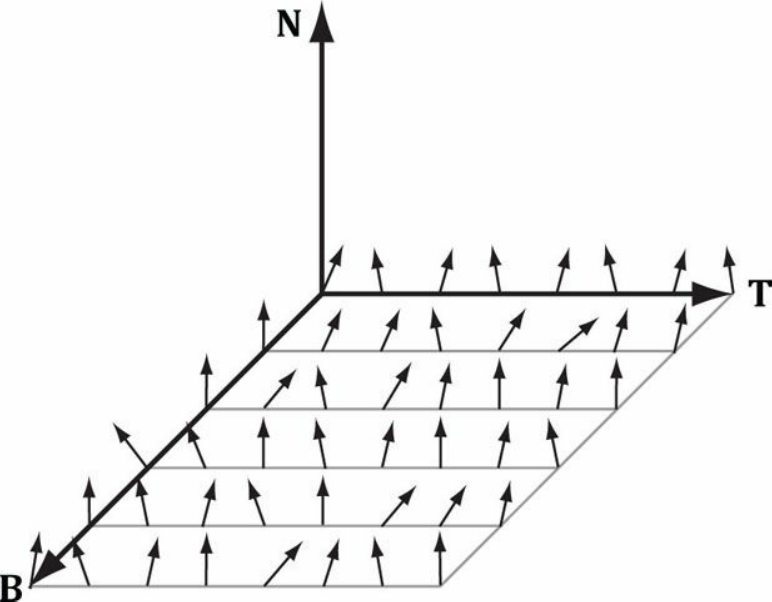
由于压缩后的法线贴图通常是以R8G8B8A8的格式存储,我们也可以直接把它当做图片来打开观察。

前面说到大部分法向量的z分量会比x, y分量大,导致整个图看起来会偏蓝。
法线贴图的压缩与解压
经过初步压缩后的法线贴图的占用空间为原来的1/4(不考虑文件头),就算每个分量只有256种表示,也足够表示出16777216种不同的法向量了。假如现在我们已经有未经过压缩的法线贴图,那要怎么进行初步压缩呢?
对于一个单位法向量来说,其任意一个分量的取值也无非就是落在[-1, 1]的区间上。现在我们要将其映射到[0, 255]的区间上,可以用下面的公式来进行压缩:
而如果现在拿到的是24位法向量,要进行还原,则可以用下面的公式:
当然,经过还原后的法向量是有部分的精度损失了,至少能够映射回[-1, 1]的区间上。
通常情况下我们能拿到的都是经过压缩后的法线贴图,但是还原工作还是需要由自己来完成。其中T表示切线空间(Tangent Space)
float3 normalT = g_NormalMap.Sample(sam, pin.tex);
经过上面的采样后,normalT的每个分量会自动从[0, 255]映射到[0, 1],但还不是最终[-1, 1]的区间。因此我们还需要完成下面这一步:
normalT = 2.0f * normalT - 1.0f;
这里的1.0f会扩展成float3(1.0f, 1.0f, 1.0f)以完成减法运算。
注意:如果你想要使用压缩纹理格式(对原来的R8G8B8A8进一步压缩)来存储法线贴图,可以使用BC7(
DXGI_FORMAT_BC7_UNORM)来获得最佳性能。在DirectXTex中有大量从BC1到BC7的纹理压缩/解压函数。
纹理/切线空间
这里开始就会产生一个疑问了,为什么需要切线空间?
在只有2D的纹理坐标系仅包含了U轴和V轴,但现在我们的纹理中存放的是法向量,这些法向量要怎么变换到局部物体上某一个三角形对应位置呢?这就需要我们对当前法向量做一次矩阵变换(平移和旋转),使它能够来到局部坐标系下物体的某处表面。由于矩阵变换涉及到的是坐标系变换,我们需要先在原来的2D纹理坐标系加一条坐标轴(N轴),与T轴(原来的U轴)和B轴(原来的V轴)相互垂直,以此形成切线空间。
一开始法向量处在单位切线空间,而需要变换到目标3D三角形的位置也有一个对应的切线空间。对于一个立方体来说,一个面的两个三角形可以共用一个切线空间。
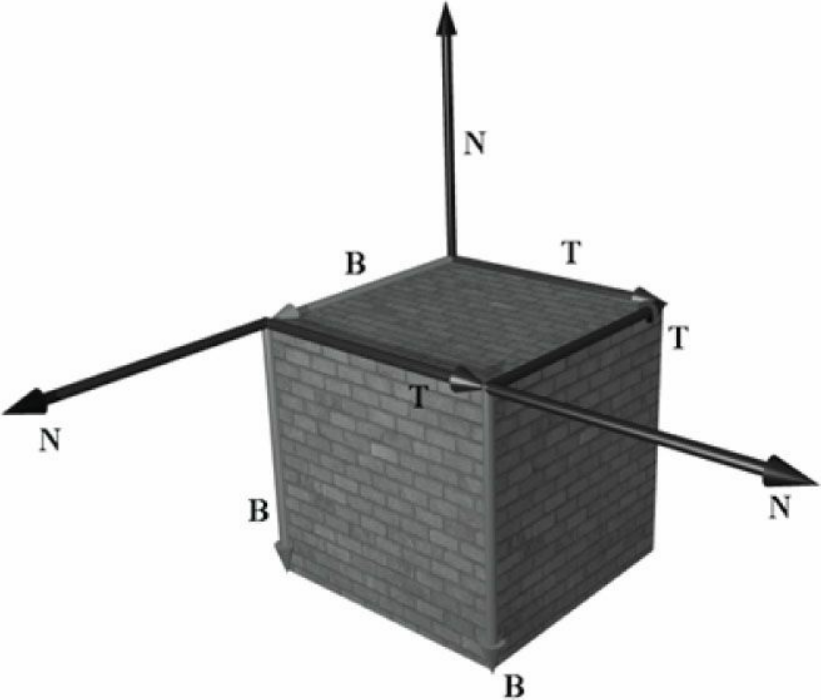
利用顶点位置和纹理坐标求TBN坐标系
现在假设我们的顶点只包含了位置和纹理坐标这两个信息,有这样一个三角形,它们的顶点为V0(x0, y0, z0), V1(x1, y1, z1), V2(x2, y2, z2),纹理坐标为(u0, v0), (u1, v1), (u2, v2)。
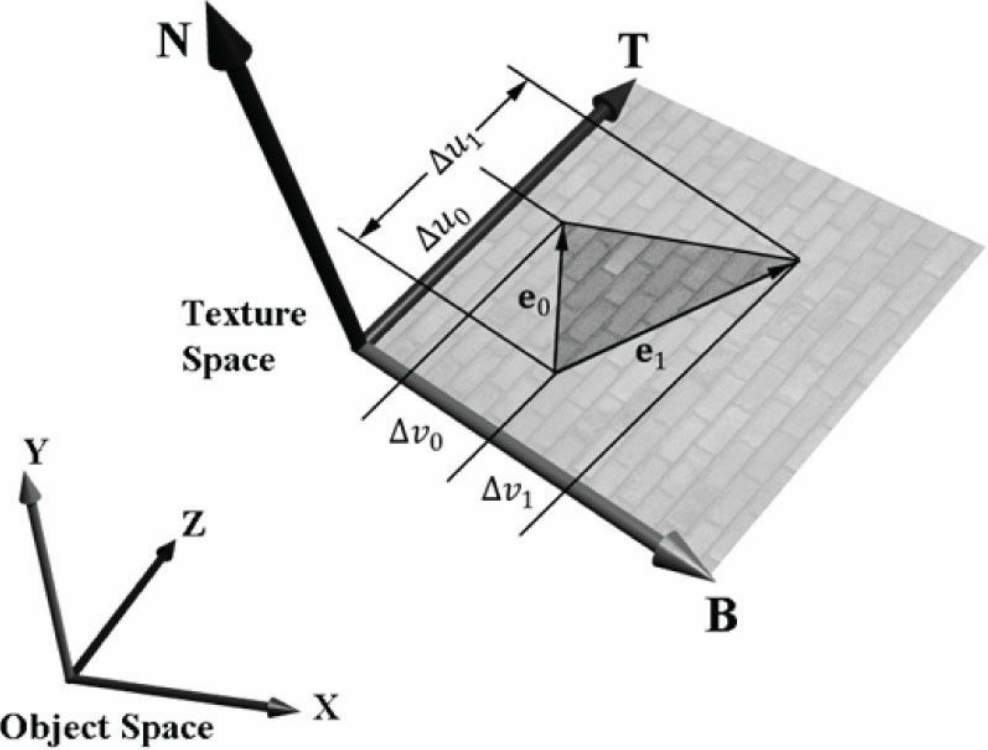
图片展示了一个三角形与所处的切线空间,我们可以这样定义向量E0和E1:
现在T轴和B轴都是待求的单位向量,可以列出下述关系:
把它用矩阵来描述:
继续细化:
为了计算TB矩阵,需要在等式两边左乘uv矩阵的逆:
对于一个二阶矩阵顶点求逆,我们不考虑过程。已知有矩阵\(\mathbf{A} = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\),那么它的逆矩阵为:
因此上面的方程最终变成:
这里可以找一个例子尝试一下:
V0坐标为(0, 0, -0.25), 纹理坐标为(0, 0.5)
V1坐标为(0.15, 0, 0), 纹理坐标为(0.3, 0)
V2坐标为(0.4, 0, 0), 纹理坐标为(0.8, 0)
求解过程如下:
由于位置坐标和纹理坐标的不一致性,导致求出来的T向量和B向量很有可能不是单位向量。仅当位置坐标的变化率与纹理坐标的变化率相同时才会得到单位向量。这里我们将其进行标准化即可。
但如果对纹理坐标进行了变换,有可能导致T轴和B轴不相互垂直。比如尝试用球体网格模型某个三角形面内的一点映射到球面上一点。
顶点切线空间
上面的运算得到的切线空间是基于单个三角形的,可以看到其运算过程还是比较复杂,而且交给着色器来进行运算的话还会产生大量的指令。
我们可以为顶点添加法向量N和切线向量T用于构建基于顶点的切线空间。很早之前提到法向量是与该顶点共用的所有三角形的法向量取平均值所得到的。切线向量也一样,它是与该顶点共用的所有三角形的切线向量取平均值所得到的。
现在Vertex.h定义了我们的新顶点类型:
struct VertexPosNormalTangentTex
{
DirectX::XMFLOAT3 pos;
DirectX::XMFLOAT3 normal;
DirectX::XMFLOAT4 tangent;
DirectX::XMFLOAT2 tex;
static D3D11_INPUT_ELEMENT_DESC_ARRAY<4> GetInputLayout()
{
static const D3D11_INPUT_ELEMENT_DESC inputLayout[4] = {
{ "POSITION", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 0, D3D11_INPUT_PER_VERTEX_DATA, 0 },
{ "NORMAL", 0, DXGI_FORMAT_R32G32B32_FLOAT, 1, 0, D3D11_INPUT_PER_VERTEX_DATA, 0 },
{ "TANGENT", 0, DXGI_FORMAT_R32G32B32A32_FLOAT, 2, 0, D3D11_INPUT_PER_VERTEX_DATA, 0 },
{ "TEXCOORD", 0, DXGI_FORMAT_R32G32_FLOAT, 3, 0, D3D11_INPUT_PER_VERTEX_DATA, 0 }
};
return inputLayout;
}
};
这里的tangent是一个4D向量,考虑到要和微软DXTK定义的顶点类型保持一致,多出来的w分量可以留作他用,这里暂不讨论。
施密特向量正交化
通常顶点提供的N和T通常是相互垂直的,并且都是单位向量,我们可以通过计算\(\mathbf{B} = \mathbf{N} \times \mathbf{T}\)来得到副法线向量B,使得顶点可以不需要存放副法线向量B。但是经过插值计算后的N和T可能会导致不是相互垂直,我们最好还是要通过施密特正交化来获得实际的切线空间。
现在已知互不垂直的N向量和T向量,我们希望求出与N向量垂直的T'向量,需要将T向量投影到N向量上。
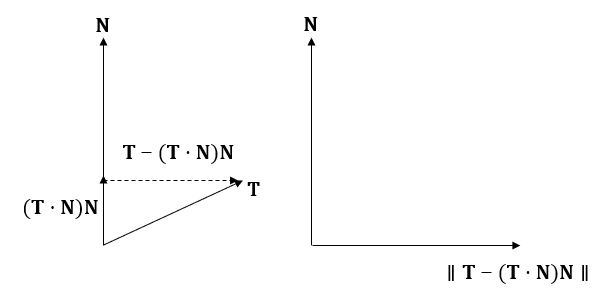
从上面的图我们可以知道最终求得的T' 为
B' 最终也可以确定下来
这样T', B', N相互垂直,可以构成TBN坐标系。在后面的着色器实现中我们也会用到这部分内容。
切线空间的变换
一开始的切线空间可以用一个单位矩阵来表示,切线向量正是处在这个空间中。紧接着就是需要对其进行一次到局部对象(具体到某个三角形)切线空间的变换:
然后切线向量随同世界矩阵一同进行变换来到世界坐标系,因此我们可以把它写成:
注意:
- 对切线向量进行矩阵变换,我们只需要使用3x3的矩阵即可。
- 法线向量变换到世界矩阵需要用世界矩阵求逆的转置进行校正,而对切线向量只需要用世界矩阵变换即可。下图演示了将宽度拉伸为原来2倍后,法线和切线向量的变化:
HLSL代码
为了使用法线贴图,我们需要完成下列步骤:
- 获取该纹理所需要用到的法线贴图,在C++端为其创建一个
ID3D11Texture2D。这里不考虑如何制作一张法线贴图。 - 对于一个网格模型来说,顶点数据需要包含位置、法向量、切线向量、纹理坐标四个元素。同样这里不讨论模型的制作,在本教程使用的是
Geometry所生成的网格模型 - 在顶点着色器中,将顶点法向量和切线向量从局部坐标系变换到世界坐标系
- 在像素着色器中,使用经过插值的法向量和切线向量来为每个三角形表面的像素点构建TBN坐标系,然后将切线空间的法向量变换到世界坐标系中,这样最终求得的法向量用于光照计算。
现在我们的Basic.hlsli沿用的是第23章动态天空盒的部分,变化如下:
Texture2D g_DiffuseMap : register(t0);
Texture2D g_NormalMap : register(t1);
TextureCube g_TexCube : register(t2);
SamplerState g_Sam : register(s0);
// 使用的是第23章的常量缓冲区,省略...
// 省略和之前一样的结构体...
struct VertexPosNormalTangentTex
{
float3 posL : POSITION;
float3 normalL : NORMAL;
float4 tangentL : TANGENT;
float2 tex : TEXCOORD;
};
struct VertexPosHWNormalTangentTex
{
float4 posH : SV_POSITION;
float3 posW : POSITION; // 在世界中的位置
float3 normalW : NORMAL; // 法向量在世界中的方向
float4 tangentW : TANGENT; // 切线在世界中的方向
float2 tex : TEXCOORD;
};
float3 NormalSampleToWorldSpace(float3 normalMapSample,
float3 unitNormalW,
float4 tangentW)
{
// 将读取到法向量中的每个分量从[0, 1]还原到[-1, 1]
float3 normalT = 2.0f * normalMapSample - 1.0f;
// 构建位于世界坐标系的切线空间
float3 N = unitNormalW;
float3 T = normalize(tangentW.xyz - dot(tangentW.xyz, N) * N); // 施密特正交化
float3 B = cross(N, T);
float3x3 TBN = float3x3(T, B, N);
// 将凹凸法向量从切线空间变换到世界坐标系
float3 bumpedNormalW = mul(normalT, TBN);
return bumpedNormalW;
}
上面的NormalSampleToWorldSpace函数用于将法向量从切线空间变换到世界空间,位于Basic.hlsli。它接受了3个参数:从法线贴图采样得到的向量,变换到世界坐标系的法向量和切线向量。
然后是顶点着色器:
// NormalMap_VS.hlsl
#include "Basic.hlsli"
// 顶点着色器
VertexPosHWNormalTangentTex VS(VertexPosNormalTangentTex vIn)
{
VertexPosHWNormalTangentTex vOut;
matrix viewProj = mul(g_View, g_Proj);
vector posW = mul(float4(vIn.posL, 1.0f), g_World);
vOut.posW = posW.xyz;
vOut.posH = mul(posW, viewProj);
vOut.normalW = mul(vIn.normalL, (float3x3) g_WorldInvTranspose);
vOut.tangentW = float4(mul(vIn.tangentL.xyz, (float3x3) g_World), vIn.tangentL.w);
vOut.tex = vIn.tex;
return vOut;
}
相比之前的像素着色器,现在它多了对法线映射的处理:
// 法线映射
float3 normalMapSample = g_NormalMap.Sample(g_Sam, pIn.tex).rgb;
float3 bumpedNormalW = NormalSampleToWorldSpace(normalMapSample, pIn.normalW, pIn.tangentW);
求得的法向量bumpedNormalW将用于光照计算。
现在完整的像素着色器代码如下:
// NormalMap_PS.hlsl
#include "Basic.hlsli"
// 像素着色器(3D)
float4 PS(VertexPosHWNormalTangentTex pIn) : SV_Target
{
float4 texColor = g_DiffuseMap.Sample(g_Sam, pIn.tex);
// 提前进行裁剪,对不符合要求的像素可以避免后续运算
clip(texColor.a - 0.1f);
// 标准化法向量和切线
pIn.normalW = normalize(pIn.normalW);
pIn.tangentW.xyz = normalize(pIn.tangentW.xyz);
// 求出顶点指向眼睛的向量,以及顶点与眼睛的距离
float3 toEyeW = normalize(g_EyePosW - pIn.posW);
float distToEye = distance(g_EyePosW, pIn.posW);
// 法线映射
float3 normalMapSample = g_NormalMap.Sample(g_Sam, pIn.tex).rgb;
float3 bumpedNormalW = NormalSampleToWorldSpace(normalMapSample, pIn.normalW, pIn.tangentW);
// 初始化为0
float4 ambient = float4(0.0f, 0.0f, 0.0f, 0.0f);
float4 diffuse = float4(0.0f, 0.0f, 0.0f, 0.0f);
float4 spec = float4(0.0f, 0.0f, 0.0f, 0.0f);
float4 A = float4(0.0f, 0.0f, 0.0f, 0.0f);
float4 D = float4(0.0f, 0.0f, 0.0f, 0.0f);
float4 S = float4(0.0f, 0.0f, 0.0f, 0.0f);
int i;
[unroll]
for (i = 0; i < 5; ++i)
{
ComputeDirectionalLight(g_Material, g_DirLight[i], bumpedNormalW, toEyeW, A, D, S);
ambient += A;
diffuse += D;
spec += S;
}
[unroll]
for (i = 0; i < 5; ++i)
{
ComputePointLight(g_Material, g_PointLight[i], pIn.posW, bumpedNormalW, toEyeW, A, D, S);
ambient += A;
diffuse += D;
spec += S;
}
[unroll]
for (i = 0; i < 5; ++i)
{
ComputeSpotLight(g_Material, g_SpotLight[i], pIn.posW, bumpedNormalW, toEyeW, A, D, S);
ambient += A;
diffuse += D;
spec += S;
}
float4 litColor = texColor * (ambient + diffuse) + spec;
// 反射
if (g_ReflectionEnabled)
{
float3 incident = -toEyeW;
float3 reflectionVector = reflect(incident, pIn.normalW);
float4 reflectionColor = g_TexCube.Sample(g_Sam, reflectionVector);
litColor += g_Material.Reflect * reflectionColor;
}
// 折射
if (g_RefractionEnabled)
{
float3 incident = -toEyeW;
float3 refractionVector = refract(incident, pIn.normalW, g_Eta);
float4 refractionColor = g_TexCube.Sample(g_Sam, refractionVector);
litColor += g_Material.Reflect * refractionColor;
}
litColor.a = texColor.a * g_Material.Diffuse.a;
return litColor;
}
所有的着色器将共用Basic.hlsli。而对BasicEffect的变化(和C++的交互)这里我们不讨论。
下面的动画演示了法线贴图的对比效果(GIF画质有点渣):

至此进阶篇就告一段落了。
DirectX11 With Windows SDK完整目录
欢迎加入QQ群: 727623616 可以一起探讨DX11,以及有什么问题也可以在这里汇报。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号