CSP-S 模拟 29
CSP-S 模拟 29
A. 一个赢家 (card)
有 \(2n\) 张卡,第 \(i\) 张卡上写着数字 \(i\)。有 \(n\) 个人,这 \(n\) 个人轮流从这些卡中均匀随机拿走两张,不放回。现在每个人手上各有两张卡,手上两张卡上写的数字的和最大的人获胜。显然,胜者可能不止一个,求胜者恰好只有一个的概率。
打表题。
首先我们可以不用考虑顺序,只需考虑方案数即可。
显然的想法是枚举 \(i,j \in [1,2n] (i\ne j)\),钦定 \(a[i]+a[j]\) 为唯一的那个最大值,计算这种情况的方案数,最后所有情况的方案数的 \(\sum\) 即为总方案数。容易发现这样所有合法情况均被包含在内。
看一个例子:
设 \(n!! = 1 \times 3 \times \dots \times n\)(保证 n 为奇数)
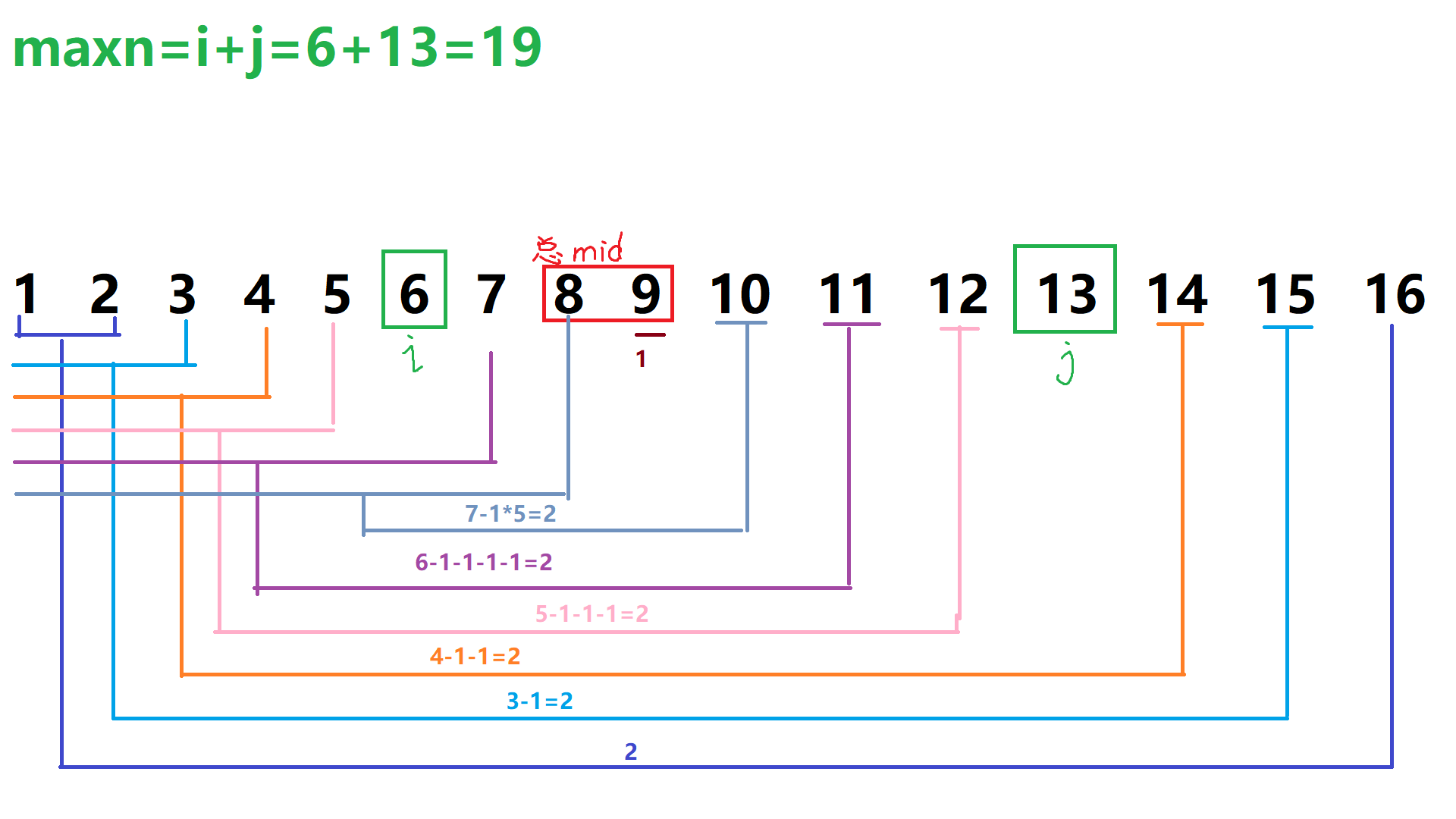
答案为 \(2^6 \times (1!!)\)
再看一个
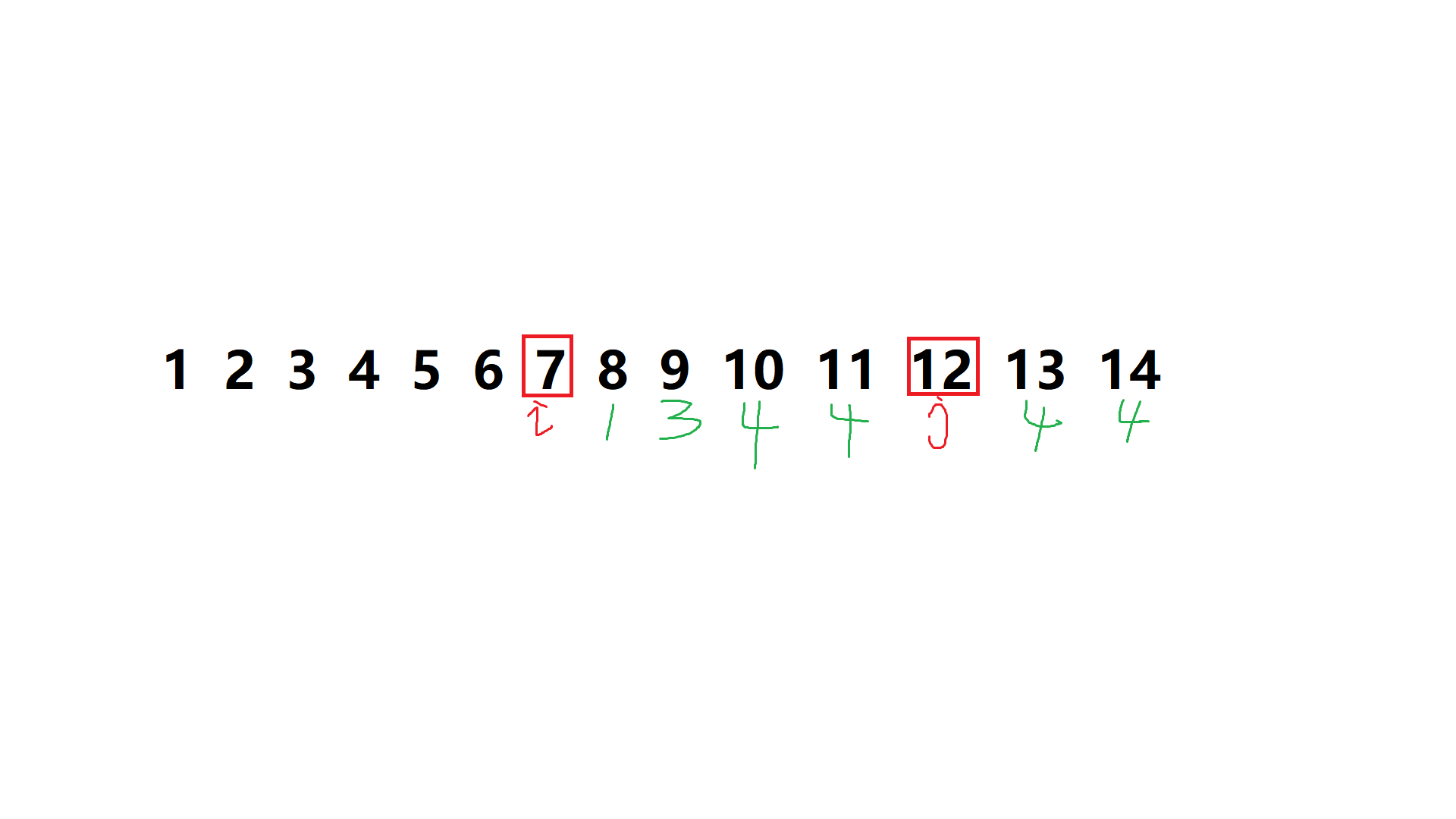
答案为 \(4^4 \times (3!!)\)
再看一个
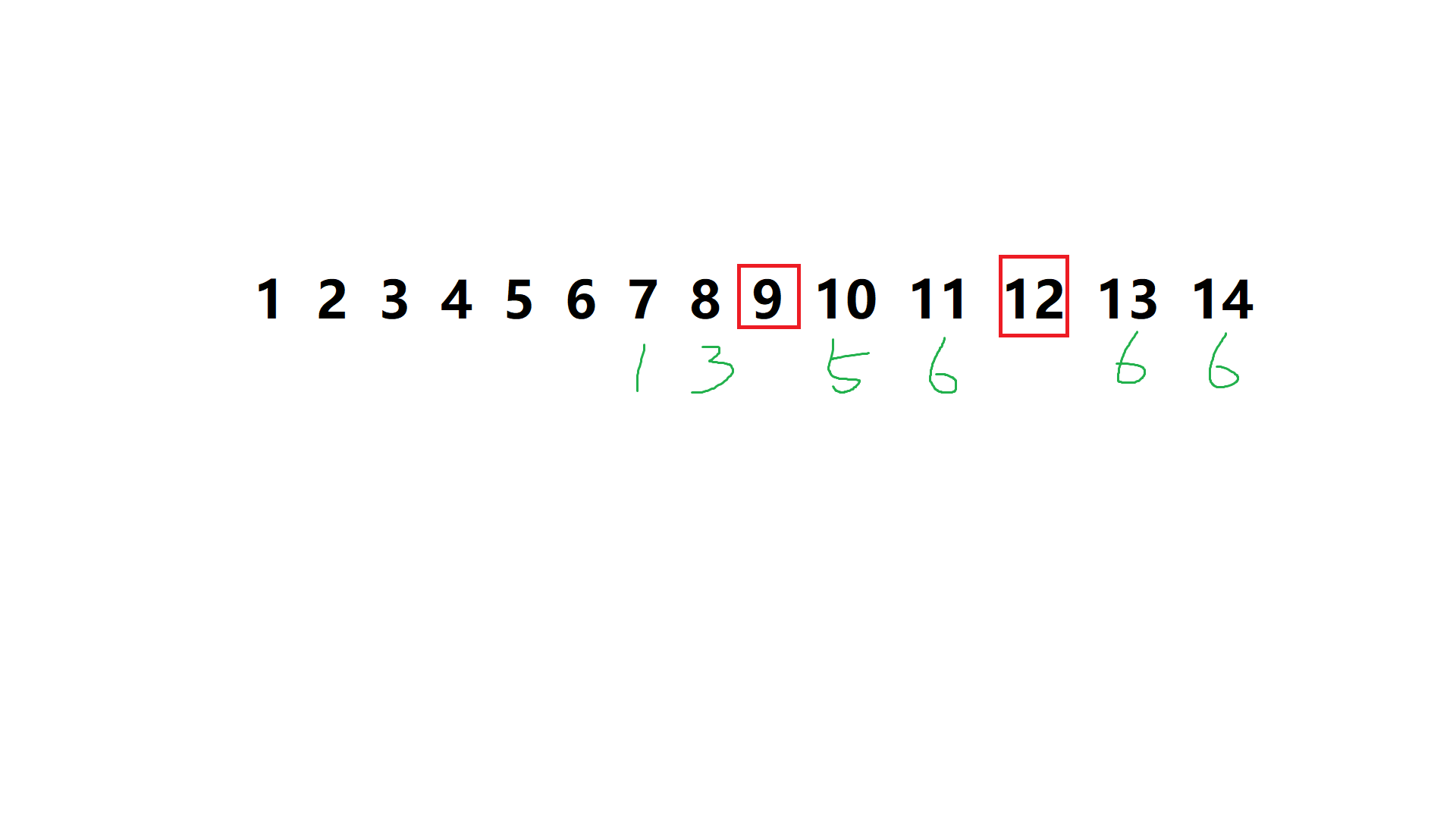
答案为 \(6^3 \times (5!!)\)
发现答案为 \(x^p \times (y!!)\) 的形式。
又通过手模发现 \(y=(2n-2)-2x-1\)
设 \(dp[i][j]\) 为钦定 \(a[i]+a[j]\) 为最大值时的方案数。
于是就有 dp 雏形了。
再打个暴力与 dp 中的每一个值相比较,修正 \(2.5h\) 即可得到以下 \(n^2\) 代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int Size=(1<<20)+1;
char buf[Size],*p1=buf,*p2=buf;
char buffer[Size];
int op1=-1;
const int op2=Size-1;
#define getchar() \
(tt == ss && (tt=(ss=In)+fread(In, 1, 1 << 20, stdin), ss == tt) \
? EOF \
: *ss++)
char In[1<<20],*ss=In,*tt=In;
inline int read()
{
int x=0,c=getchar(),f=0;
for(;c>'9'||c<'0';f=c=='-',c=getchar());
for(;c>='0'&&c<='9';c=getchar())
x=(x<<1)+(x<<3)+(c^48);
return f?-x:x;
}
inline void write(int x)
{
if(x<0) x=-x,putchar('-');
if(x>9) write(x/10);
putchar(x%10+'0');
}
const int mod=1e9+7;
int n;
int ksm(int x,int p)
{
if(x<=0||p<0) return 1;
int ans=1;
while(p)
{
if(p&1) ans*=x,ans%=mod;
x*=x;
x%=mod;
p>>=1;
}
return ans;
}
const int N=5e6+5;
int f[N],frac[N<<1],frac2[N<<1];
int sum[N],sum2[N];
int g[N];
int tot;
void init()
{
int maxn=5e6;
f[0]=1;
int tot=1;
frac[0]=g[0]=frac[1]=1;
frac2[0]=frac2[1]=1;
g[1]=2;
for(int i=2;i<=n;i++)
{
frac[i]=frac[i-1]*i%mod;
frac2[i]=frac2[i-2]*i%mod;
g[i]=g[i-1]*2%mod;
}
for(int i=1;i<=(n>>1);i++) g[i]=ksm(g[i],mod-2);
for(int i=1;i<=(n>>1);i++) f[i]=frac[i<<1]*g[i]%mod;
}
signed main()
{
//card.in
n=read()<<1;
init();
if(n==2) { cout<<"1"; return 0; }
int ans=0;
for(int r=n;r>(n>>1);r--,cout<<"\n")
for(int l=r-1;l>n-r+1;l--)
{
int nw=ans;
int mid=(l+r+2)>>1;
if(mid<=(n>>1)) break;
ans+=ksm(l-(n-r)-1,n-mid)*frac2[max(0ll,(n-2-(max(0ll,n-mid)<<1))-1)]%mod;
ans%=mod;
cout<<"l="<<l<<" r="<<r<<" ksm="<<ksm(l-(n-r)-1,n-mid)<<" frac2="<<frac2[max(0ll,(n-2-(max(0ll,n-mid)<<1))-1)]<<" ans="<<ans<<" dtans="<<ans-nw<<"\n";
}
cout<<ans*ksm(frac2[n-1],mod-2)%mod<<"\n";
return 0;
}
如果你有惊人的注意力,你可以发现:友情链接
而这里是打表。
以 \(n=5\) 为例。打出 \(i,j,dp[i][j]\)。
其中 \(dtans=dp[i][j]=ksm\times frac2\pmod {mod}\ , ans=\sum dtans\pmod {mod}\)。
使用 ctrl+F。第一区块选中 \(ksm\) 和 \(frac2\),查看出现次数。
例:ksm=1 frac2=34459425
l=19 r=20 ksm=1 frac2=34459425 ans=34459425 dtans=34459425
l=18 r=20 ksm=1 frac2=34459425 ans=68918850 dtans=34459425
l=17 r=20 ksm=16 frac2=2027025 ans=101351250 dtans=32432400
l=16 r=20 ksm=15 frac2=2027025 ans=131756625 dtans=30405375
l=15 r=20 ksm=196 frac2=135135 ans=158243085 dtans=26486460
l=14 r=20 ksm=169 frac2=135135 ans=181080900 dtans=22837815
l=13 r=20 ksm=1728 frac2=10395 ans=199043460 dtans=17962560
l=12 r=20 ksm=1331 frac2=10395 ans=212879205 dtans=13835745
l=11 r=20 ksm=10000 frac2=945 ans=222329205 dtans=9450000
l=10 r=20 ksm=6561 frac2=945 ans=228529350 dtans=6200145
l=9 r=20 ksm=32768 frac2=105 ans=231969990 dtans=3440640
l=8 r=20 ksm=16807 frac2=105 ans=233734725 dtans=1764735
l=7 r=20 ksm=46656 frac2=15 ans=234434565 dtans=699840
l=6 r=20 ksm=15625 frac2=15 ans=234668940 dtans=234375
l=5 r=20 ksm=16384 frac2=3 ans=234718092 dtans=49152
l=4 r=20 ksm=2187 frac2=3 ans=234724653 dtans=6561
l=3 r=20 ksm=256 frac2=1 ans=234724909 dtans=256
l=2 r=20 ksm=1 frac2=1 ans=234724910 dtans=1
l=18 r=19 ksm=16 frac2=2027025 ans=267157310 dtans=32432400
l=17 r=19 ksm=15 frac2=2027025 ans=297562685 dtans=30405375
l=16 r=19 ksm=196 frac2=135135 ans=324049145 dtans=26486460
l=15 r=19 ksm=169 frac2=135135 ans=346886960 dtans=22837815
l=14 r=19 ksm=1728 frac2=10395 ans=364849520 dtans=17962560
l=13 r=19 ksm=1331 frac2=10395 ans=378685265 dtans=13835745
l=12 r=19 ksm=10000 frac2=945 ans=388135265 dtans=9450000
l=11 r=19 ksm=6561 frac2=945 ans=394335410 dtans=6200145
l=10 r=19 ksm=32768 frac2=105 ans=397776050 dtans=3440640
l=9 r=19 ksm=16807 frac2=105 ans=399540785 dtans=1764735
l=8 r=19 ksm=46656 frac2=15 ans=400240625 dtans=699840
l=7 r=19 ksm=15625 frac2=15 ans=400475000 dtans=234375
l=6 r=19 ksm=16384 frac2=3 ans=400524152 dtans=49152
l=5 r=19 ksm=2187 frac2=3 ans=400530713 dtans=6561
l=4 r=19 ksm=256 frac2=1 ans=400530969 dtans=256
l=3 r=19 ksm=1 frac2=1 ans=400530970 dtans=1
l=17 r=18 ksm=196 frac2=135135 ans=427017430 dtans=26486460
l=16 r=18 ksm=169 frac2=135135 ans=449855245 dtans=22837815
l=15 r=18 ksm=1728 frac2=10395 ans=467817805 dtans=17962560
l=14 r=18 ksm=1331 frac2=10395 ans=481653550 dtans=13835745
l=13 r=18 ksm=10000 frac2=945 ans=491103550 dtans=9450000
l=12 r=18 ksm=6561 frac2=945 ans=497303695 dtans=6200145
l=11 r=18 ksm=32768 frac2=105 ans=500744335 dtans=3440640
l=10 r=18 ksm=16807 frac2=105 ans=502509070 dtans=1764735
l=9 r=18 ksm=46656 frac2=15 ans=503208910 dtans=699840
l=8 r=18 ksm=15625 frac2=15 ans=503443285 dtans=234375
l=7 r=18 ksm=16384 frac2=3 ans=503492437 dtans=49152
l=6 r=18 ksm=2187 frac2=3 ans=503498998 dtans=6561
l=5 r=18 ksm=256 frac2=1 ans=503499254 dtans=256
l=4 r=18 ksm=1 frac2=1 ans=503499255 dtans=1
l=16 r=17 ksm=1728 frac2=10395 ans=521461815 dtans=17962560
l=15 r=17 ksm=1331 frac2=10395 ans=535297560 dtans=13835745
l=14 r=17 ksm=10000 frac2=945 ans=544747560 dtans=9450000
l=13 r=17 ksm=6561 frac2=945 ans=550947705 dtans=6200145
l=12 r=17 ksm=32768 frac2=105 ans=554388345 dtans=3440640
l=11 r=17 ksm=16807 frac2=105 ans=556153080 dtans=1764735
l=10 r=17 ksm=46656 frac2=15 ans=556852920 dtans=699840
l=9 r=17 ksm=15625 frac2=15 ans=557087295 dtans=234375
l=8 r=17 ksm=16384 frac2=3 ans=557136447 dtans=49152
l=7 r=17 ksm=2187 frac2=3 ans=557143008 dtans=6561
l=6 r=17 ksm=256 frac2=1 ans=557143264 dtans=256
l=5 r=17 ksm=1 frac2=1 ans=557143265 dtans=1
l=15 r=16 ksm=10000 frac2=945 ans=566593265 dtans=9450000
l=14 r=16 ksm=6561 frac2=945 ans=572793410 dtans=6200145
l=13 r=16 ksm=32768 frac2=105 ans=576234050 dtans=3440640
l=12 r=16 ksm=16807 frac2=105 ans=577998785 dtans=1764735
l=11 r=16 ksm=46656 frac2=15 ans=578698625 dtans=699840
l=10 r=16 ksm=15625 frac2=15 ans=578933000 dtans=234375
l=9 r=16 ksm=16384 frac2=3 ans=578982152 dtans=49152
l=8 r=16 ksm=2187 frac2=3 ans=578988713 dtans=6561
l=7 r=16 ksm=256 frac2=1 ans=578988969 dtans=256
l=6 r=16 ksm=1 frac2=1 ans=578988970 dtans=1
l=14 r=15 ksm=32768 frac2=105 ans=582429610 dtans=3440640
l=13 r=15 ksm=16807 frac2=105 ans=584194345 dtans=1764735
l=12 r=15 ksm=46656 frac2=15 ans=584894185 dtans=699840
l=11 r=15 ksm=15625 frac2=15 ans=585128560 dtans=234375
l=10 r=15 ksm=16384 frac2=3 ans=585177712 dtans=49152
l=9 r=15 ksm=2187 frac2=3 ans=585184273 dtans=6561
l=8 r=15 ksm=256 frac2=1 ans=585184529 dtans=256
l=7 r=15 ksm=1 frac2=1 ans=585184530 dtans=1
l=13 r=14 ksm=46656 frac2=15 ans=585884370 dtans=699840
l=12 r=14 ksm=15625 frac2=15 ans=586118745 dtans=234375
l=11 r=14 ksm=16384 frac2=3 ans=586167897 dtans=49152
l=10 r=14 ksm=2187 frac2=3 ans=586174458 dtans=6561
l=9 r=14 ksm=256 frac2=1 ans=586174714 dtans=256
l=8 r=14 ksm=1 frac2=1 ans=586174715 dtans=1
l=12 r=13 ksm=16384 frac2=3 ans=586223867 dtans=49152
l=11 r=13 ksm=2187 frac2=3 ans=586230428 dtans=6561
l=10 r=13 ksm=256 frac2=1 ans=586230684 dtans=256
l=9 r=13 ksm=1 frac2=1 ans=586230685 dtans=1
l=11 r=12 ksm=256 frac2=1 ans=586230941 dtans=256
l=10 r=12 ksm=1 frac2=1 ans=586230942 dtans=1
458729432
找到规律了吧!
出现次数从上至下:1 1 2 2 3 3 4 4 ....
所以我们只用枚举第一区块,对答案的贡献次数很容易求出。
这题就做完了。
你赛后发现这是有道理的,相当于固定最大值,找到有几个合法的位置,发现当前答案和位置无关。
概率要乘总方案数的逆元。即 \(\frac{1}{(2n-1)!!}\pmod {mod}\)
Code:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int Size=(1<<20)+1;
char buf[Size],*p1=buf,*p2=buf;
char buffer[Size];
int op1=-1;
const int op2=Size-1;
#define getchar() \
(tt == ss && (tt=(ss=In)+fread(In, 1, 1 << 20, stdin), ss == tt) \
? EOF \
: *ss++)
char In[1<<20],*ss=In,*tt=In;
inline int read()
{
int x=0,c=getchar(),f=0;
for(;c>'9'||c<'0';f=c=='-',c=getchar());
for(;c>='0'&&c<='9';c=getchar())
x=(x<<1)+(x<<3)+(c^48);
return f?-x:x;
}
inline void write(int x)
{
if(x<0) x=-x,putchar('-');
if(x>9) write(x/10);
putchar(x%10+'0');
}
const int mod=1e9+7;
int n;
int ksm(int x,int p)
{
if(x<=0||p<0) return 1;
int ans=1;
while(p)
{
if(p&1) ans*=x,ans%=mod;
x*=x;
x%=mod;
p>>=1;
}
return ans;
}
const int N=5e6+5;
int frac2[N];
int tot;
void init()
{
int maxn=n>>1;
int tot=1;
frac2[0]=1;//frac2[1]=1;
for(int i=1;i<=maxn;i++) frac2[i]=frac2[i-1]*((i<<1)|1)%mod;
}
signed main()
{
freopen("card.in","r",stdin);
freopen("card.out","w",stdout);
n=read()<<1;
init(); if(n==2) { cout<<"1"; return 0; }
int ans=0,nwcnt=1,r=n;
for(int l=r-1;l>1;l--)
{
nwcnt++;
int nw=ans;
int mid=(l+r+2)>>1;
ans+=ksm(l-(n-r)-1,n-mid)*frac2[max(0ll,(n-2-(max(0ll,n-mid)<<1))-1)>>1]%mod*(nwcnt>>1)%mod;
ans%=mod;
}
cout<<ans*ksm(frac2[(n-1)>>1],mod-2)%mod<<"\n";
return 0;
}
(大道至简)
B. 排列计数 (count)

显然不会。有简单做法。
先把每个数所有的平方因子踢出,再把无平方因子的这些数放到数组 \(a\) 中。
发现当且仅当答案排列 \(\exists p[i] = p[i-1]\) 时,该排列不合法。就是答案排列不能有两个相邻的数相等。
设两个相邻的数相等为一个不合法数对。
我们先将 \(a\) 从小到大排序,统计每个数的出现次数,然后去重。
直接设 \(dp[i][j]\) 表示当前选完前 \(i -1\) 个数字(所有 \(< a[i]\) 的数字均被选),有 \(j\) 组不合法数对的方案数。
目标 \(dp[siz+1][0]\)。\(siz\) 为去重之后 \(a\) 数组大小。
设去重之前 \(a[i]\) 共有 \(cnt[a[i]]\) 个。
那么转移时我们枚举:
\(j\):选第 \(i\) 个数字之前不合法的数对有 \(j\) 个。
\(k\):选完第 \(i\) 个数字之后不合法的数对有 \(k\) 个。
\(c\):破坏原来的 \(c\) 组不合法数对。即为在这 \(c\) 组数对中间均先插入一个 \(a[i]\)。
\(New=k-(j-c)\) 可以直接计算出:需要新加 \(New\) 组不合法数对。
我们拆分我们的转移步骤为:先破坏原先 \(c\) 组不合法数对,再新添加 \(New\) 个不合法数对。
显然如果 \(New < 0\) 直接跳过。(你不可能新加 \(<0\) 个不合法数对。
我们现在考虑求方案数。
设 \(sum=\sum_{j=1}^{i-1} cnt[a[i]]\)。
从转移步骤一步一步求:
首先原来有 \(dp[i][j]\) 种方案。
使用两次插板法:
\(C_{cnt-1}^{cnt-1-New}\) 插出 \(cnt-New\) 个段,这样就会新添 \(New\) 组不合法数对。
\(cnt-New\) 个段的贡献分为两部分:
先在原先 \(j\) 组中随机破坏 \(c\) 组,\(C_j^c\)
剩下 \(cnt-New-c\) 个段插入除原先 \(j\) 组中间其余的地方,一共有 \(sum+1-j\) 个,\(C^{sum+1-j}_{cnt-New-c}\)。
这 \(cnt\) 个 \(a[i]\) 可以任意排列,\(A^{cnt}_{cnt}=cnt!\)。
其中若 \(C()\) 或 \(A()\) 不合法,令答案为 \(0\)。
相乘即可。设答案为 \(nw\)。
那么转移:\(dp[i+1][k]+ nw \to dp[i+1][k]\) 即可。
时间复杂度 \(O(x) << O(n^3)\),实测最大点 \(O(3.3n^2)\)。
Code:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int Size=(1<<20)+1;
char buf[Size],*p1=buf,*p2=buf;
char buffer[Size];
int op1=-1;
const int op2=Size-1;
#define getchar() \
(tt == ss && (tt=(ss=In)+fread(In, 1, 1 << 20, stdin), ss == tt) \
? EOF \
: *ss++)
char In[1<<20],*ss=In,*tt=In;
inline int read()
{
int x=0,c=getchar(),f=0;
for(;c>'9'||c<'0';f=c=='-',c=getchar());
for(;c>='0'&&c<='9';c=getchar())
x=(x<<1)+(x<<3)+(c^48);
return f?-x:x;
}
inline void write(int x)
{
if(x<0) x=-x,putchar('-');
if(x>9) write(x/10);
putchar(x%10+'0');
}
int n;
const int N=1005;
int a[N];
int b[100000],cnt;
int dp[N][N];
const int mod=1e9+7;
int find(int x)
{
for(int i=1;i<=cnt&&b[i]<=x;i++)
while(x%b[i]==0) x/=b[i];
return x;
}
int frac[1005],g[1005];
int ksm(int x,int p)
{
int ans=1;
while(p)
{
if(p&1) ans*=x,ans%=mod;
x*=x;
x%=mod;
p>>=1;
}
return ans;
}
inline int A(int n,int m)
{
if(n<0||m<0||n-m<0) return 0;
return frac[n]*g[n-m]%mod;
}
inline int C(int n,int m)
{
if(n<0||m<0||n-m<0) return 0;
return frac[n]*g[m]%mod*g[n-m]%mod;
}
void init()
{
frac[0]=g[0]=1;
for(int i=1;i<=1000;i++)
{
frac[i]=frac[i-1]*i%mod;
g[i]=ksm(frac[i],mod-2);
// cout<<frac[i]<<" "<<g[i]<<"\n";
}
}
int max(int x,int y) { return x>y?x:y; }
int min(int x,int y) { return x<y?x:y; }
void solve()
{
vector<int> v;
map<int,int> mp;
memset(dp,0,sizeof(dp));
// mp.clear();
// v.clear();
n=read();
for(int i=1;i<=n;i++)
{
int x=read();
a[i]=find(x);
mp[a[i]]++;
if(mp[a[i]]==1) v.push_back(a[i]);
}
// for(int i:v) cout<<i<<" ";
// for(int i=1;i<=n;i++) cout<<a[i]<<" ";
// cout<<"\n";
// int ans=0;
sort(v.begin(),v.end());
sort(a+1,a+1+n);
int sum=0;
dp[0][0]=1;
for(int i=0;i<v.size();i++)
{
int num=v[i],cnt=mp[v[i]];
for(int j=0;j<max(1ll,sum);j++) // 初态不合法
if(dp[i][j])
{
for(int k=0;k<j+cnt;k++) // 末态不合法
for(int c=min(j,cnt);c>=0;c--) // 取消原先不合法
{
int last=j-c;//剩的不合法
int New=k-last;
if(last>k) {/*cout<<"Failed on #1\n";*/break;}
// cout<<dp[i][j]<<" "<<A(cnt,cnt)<<" "<<C(cnt-1,cnt-1-New)<<" "<<C(j,c)<<" "<<C(sum+1-j,cnt-New-c)<<"\n";
dp[i+1][k]+=dp[i][j]*A(cnt,cnt)%mod*C(cnt-1,cnt-1-New)%mod*C(j,c)%mod*C(sum+1-j,cnt-New-c)%mod;
dp[i+1][k]%=mod;
// cout<<dp[i+1][k]<<"\n";
}
}
sum+=cnt;
}
cout<<dp[v.size()][0]<<"\n";
}
signed main()
{
// count
// freopen("a.in","r",stdin);
// freopen("a.out","w",stdout);
freopen("count.in","r",stdin);
freopen("count.out","w",stdout);
init();
// cout<<frac[2]<<" "<<g[2]<<" "<<g[0]<<" "<<frac[2]*g[2]%mod*g[0]%mod<<"\n";
for(int i=2;i*i<=1000000000;i++) b[++cnt]=i*i;//,mp[i*i]=1;
// cout<<cnt<<"\n";
int T=read();
while(T--) solve();
return 0;
}
C. 树上染黑 (black)
树上求期望。咕。
Code:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1 << 20;
const int mod = 998244353;
int n, a[N];
int siz[N];
int frac[N], g[N];
vector<int> E[N];
int qpow(int x, int y)
{
int ans = 1, mi = x;
while (y)
{
if (y & 1)
ans = ans * mi % mod;
mi = mi * mi % mod;
y >>= 1;
}
return ans;
}
void dfs1(int x, int f)
{
siz[x] = 1;
for (int y : E[x])
{
if (f == y)
continue;
dfs1(y, x);
siz[x] += siz[y];
}
}
void dfs2(int x, int f)
{
for (int y : E[x])
{
if (f == y)
continue;
a[y] = (a[x] + g[n - siz[y] + 1] - g[siz[y] + 1] + mod) % mod;
dfs2(y, x);
}
}
signed main()
{
freopen("black.in", "r", stdin);
freopen("black.out", "w", stdout);
cin >> n;
for (int i = 1; i < n; i++)
{
int u, v;
cin >> u >> v;
E[u].push_back(v);
E[v].push_back(u);
}
dfs1(1, 0);
frac[0] = 1;
g[0] = 1;
g[1] = 1;
for (int i = 2; i <= N; i++)
g[i] = (mod - (mod / i) * g[mod % i] % mod) % mod;
for (int i = 1; i <= N; i++)
frac[i] = frac[i - 1] * i % mod;
for (int i = 1; i <= n; i++)
a[1] = (a[1] + g[siz[i] + 1]) % mod;
dfs2(1, 0);
for (int i = 1; i <= n; i++)
{
int sum = (n - 1 + g[n + 1] - a[i] + mod) % mod;
int ans = ((n - 1) * frac[n - 1] + frac[n] * sum % mod + mod) % mod;
cout << ans << '\n';
}
return 0;
}
D. 摆放花盆 (gardener)
Code:
以下是博客签名,正文无关
本文来自博客园,作者:Wy_x,转载请在文首注明原文链接:https://www.cnblogs.com/Wy-x/p/19144398
版权声明:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议(CC-BY-NC-SA 4.0 协议)进行许可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号