dijkstra 单源最短路算法 学习笔记

思想

利用贪心，BFS。

首先确定一个起始点 \(s\)。
需要两个数组 \(dist\) 和 \(vis\)。\(dist_i\) 表示编号为 \(i\) 的点到起始点 \(s\) 的最短距离，\(vis_i\) 表示编号为 \(i\) 的点是否已经确定为到起始点路径最短的点。

做法：从 起始点 \(s\) 开始，遍历与 \(s\) 相关联的所有出边（相当于BFS），对于每一组没有被 \(vis\) 数组标记的点进行松弛操作，即对这些点的 \(dist\) 数组进行更新（显然，遍历前需要将 \(vis_s\) 打上标记）。

更新完毕之后，查找所有 \(vis\) 没被标记的点，找出这些点中 \(dist\) 值最小的，作为新的起始点，并将这个 \(dist\) 最小的点的 \(vis\) 打上标记，然后按照上面同样的操作，遍历当前这个起始点的所有出边，进行松弛操作。

重复这个过程，直到所有的点都被打上了 \(vis\) 标记，那么整个求解最短路问题也就完成了。

特性

不适用于有负边权的图中。

根据上面的 dijkstra 单源最短路求解过程，我们发现整个过程都是基于贪心的思想，找到当前 \(dist\) 最小的点，打上 \(vis\) 标记就表示这个点已经被确认了，即无论接下来怎么样操作，这个点的 \(dist\) 都是最短的，因为如果有其他的路径，那么从起始点出发的第一条边就已经比当前的 \(dist\) 大了，何况接下来的边权还会让该路径长度变长，所以其他路径一定是不合法的。

但，接下来的边权一定还会让该路径的长度变长吗？如果接下来的边权是负数的话，就可能存在更短的路径了。这也就验证了为什么 dijkstra 算法不适用于有负边权的图中。

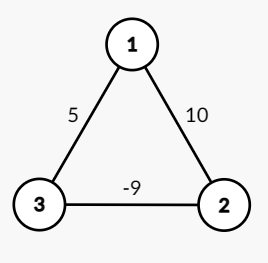
例如：在下面这个图中，我们若想求从 \(1\) 到 \(3\) 的最短路径，dijkstra 算法求解出来的最短路径是 \(5\)（直接从 \(1\) 号顶点到 \(3\) 号顶点）。但事实上的最短路径应该是 \(1\) （从 \(1\) 号顶点到 \(2\) 号顶点再到 \(3\) 号顶点）。我们来分析下 dijkstra 在这张图中犯的错误。
首先起始点为 \(1\)，遍历所有的出边，也就是 \(1->3\)这条边权为 \(5\) 的边和 \(1->2\)这条边权为 \(10\) 的边。这时 \(dist_3=5\) \(dist_2=10\)，然后取 \(dist\) 最小的且 \(vis\) 没被打上标记的点，也就是 \(3\) 号顶点，这时将 \(3\) 号顶点的 \(vis\) 打上标记，就意味着这已经是最短的路径了，之后也不会再更改了。但实际上所谓的比较长的路径 \(1->2\) 这条边，后面有一条 \(2->3\) 的负边权的边可以帮助他减少路径长度。
但如果没有负边权，毫无疑问 dijkstra 的做法是完全正确的，因为无论如何其他的路径都无法再减少长度了。

代码

我们令一个图中的点的个数为 \(n\)，边的个数为 \(m\)。
按照当前的思路来看，我们对每个点进行遍历，复杂度为 \(O(n)\)。
每次寻找所有 \(vis\) 未标记的所有点中的最小值，复杂度为 \(O(n)\)。
对每条边都要进行一次松弛操作，复杂度为 \(O(m)\)。
故总的时间复杂度为 \(O(n^2+m)\)。

考虑堆优化，使用优先队列，考虑到我们可以将优先队列更改为小根堆，每次取出队头的元素就是最小值，那么我们查找最小值的操作复杂度可以优化为 \(O(logn)\)。
再用邻接表代替邻接矩阵，最终复杂度可以达到 \(O((M+N)log N)\)。

代码实现：

struct point{
	int id,dis;
	friend bool operator < (point a,point b){
		return a.dis > b.dis;
	}
};
priority_queue<point> q;
int dist[N];
bool vis[N];
void dijkstra(){
	memset(dist,0x3f,sizeof(dist));
	dist[s] = 0;
	q.push((point){s,0});
	while (!q.empty()){
		int tmp = q.top().id;
		q.pop();
		if (!vis[tmp]){
			vis[tmp] = 1;
			for (int i = head[tmp];i;i = e[i].nxt){
				int v = e[i].to;
				int w = e[i].w;
				if (dist[v] > dist[tmp] + w){
					dist[v] = dist[tmp] + w;
					q.push((point){v,dist[tmp] + w});
				}
			}
		}
	}
}