插值与样条
先讲些题外话,前几天国庆回老家,在家中翻出了十年前大学时的一些教材课本,翻了几本看了看竟然如此的陌生。想当年考试前那么地刻苦学习,拼了命地上自习,到如今变成了一场空,真令人唏嘘。其中有一本教材是《数值分析》,这门课也是挺难的,至少现在让我看是完全看不懂了。而《数值分析》一开始就是讲插值的,可以说插值是这门课的基础。
在离散数据的基础上补插连续函数,使得这条连续曲线通过全部给定的离散数据点。插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。插值可以用于填充图像变换时像素之间的空隙。插值,拟合,逼近是数值分析的三大基础工具,通俗意义上它们的区别在于:插值是已知点列并且完全经过点列;拟合是已知点列,从整体上靠近它们,逼近是已知曲线,或者点列,通过逼近使得构造的函数无限靠近它们。科学和工程问题可以通过诸如采样、实验等方法获得若干离散的数据,根据这些数据,我们往往希望得到一个连续的函数(也就是曲线)或者更加密集的离散方程与已知数据相吻合。
插值问题的提法是:假定区间[a,b]上的实值函数f(x)在该区间上 n+1个互不相同点x0,x1……xn 处的值是f (x0),……f(xn),要求估算f(x)在[a,b]中某点x*的值。基本思路是,找到一个函数P(x),在x0,x1……xn 的节点上与f(x)函数值相同(有时,甚至一阶导数值也相同),用P(x*)的值作为函数f(x*)的近似。简单地讲就是已知数据上的若干值,为其补上未知的值。
样条方程是一类分段光滑、并且在各段交接处也有一定光滑性的函数。样条一词来源于工程绘图人员为了将一些指定点连接成一条光顺曲线所使用的工具,即富有弹性的细木条或薄钢条。由这样的样条形成的曲线在连接点处具有连续的坡度与曲率。分段低次多项式、在分段处具有一定光滑性的函数插值就是模拟以上原理发展起来的,它克服了高次多项式插值可能出现的振荡现象,具有较好的数值稳定性和收敛性,由这种插值过程产生的函数就是多项式样条函数。
在计算机被使用之前,数字演算用手工完成。虽然分段定义的象signum函数或阶梯函数这样的函数也被用到,一般人更喜欢多项式因为它们比较容易算。随着计算机的发展,样条变得越来越重要。它们一开始是作为多项式在插值中的替代品,后来又作为在计算机图形学中构造光滑和可变形状的工具。样条函数的研究始于20世纪中叶,到了60年代它与计算机辅助设计相结合,在外形设计方面得到成功的应用。样条理论已成为函数逼近的有力工具。它的应用范围也在不断扩大,不仅在数据处理、数值微分、数值积分、微分方程和积分方程数值解等数学领域有广泛的应用,而且与最优控制、变分问题、统计学、计算几何与泛函分析等学科均有密切的联系。
讲了这么多,其实我这篇博客的目的是秀一下我所实现的样条曲线,请看下面的软件截图:
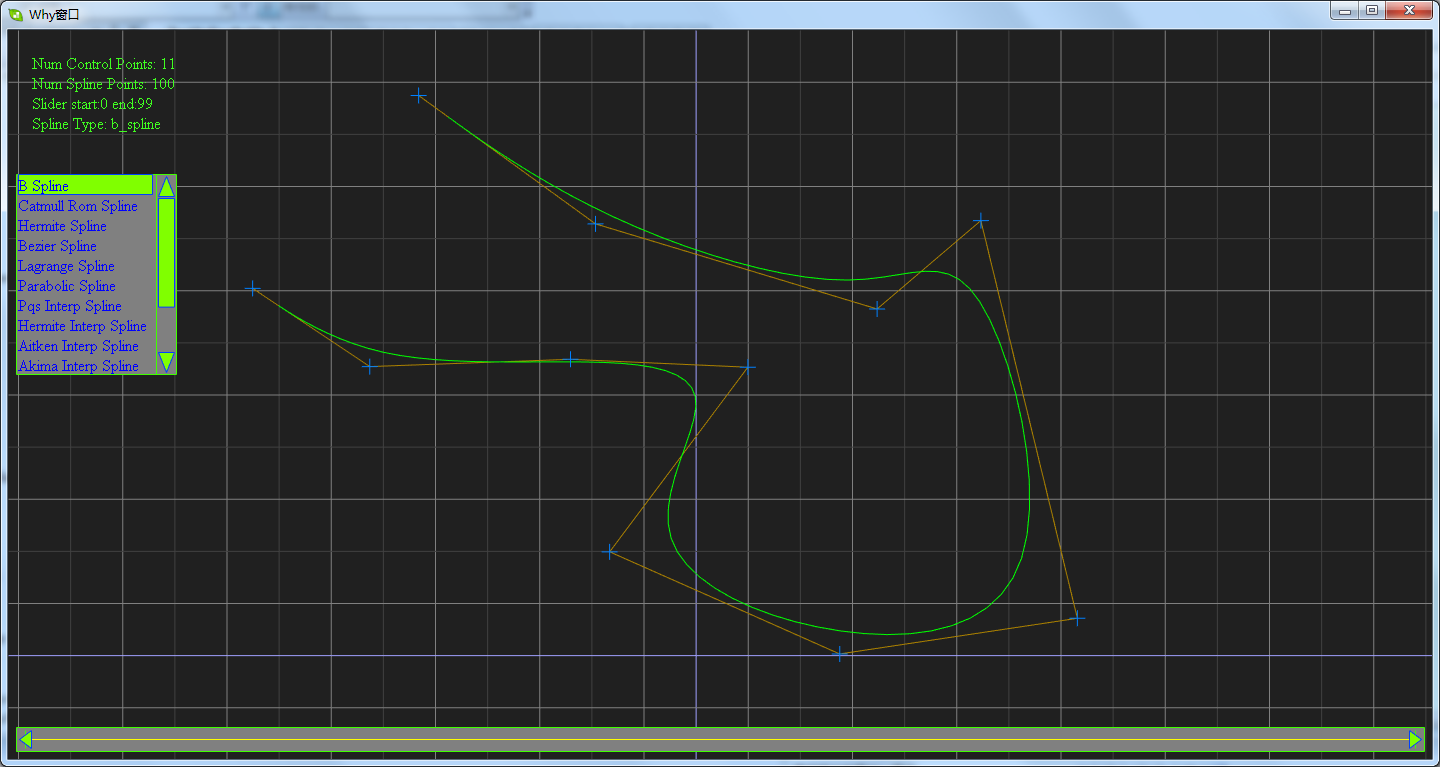
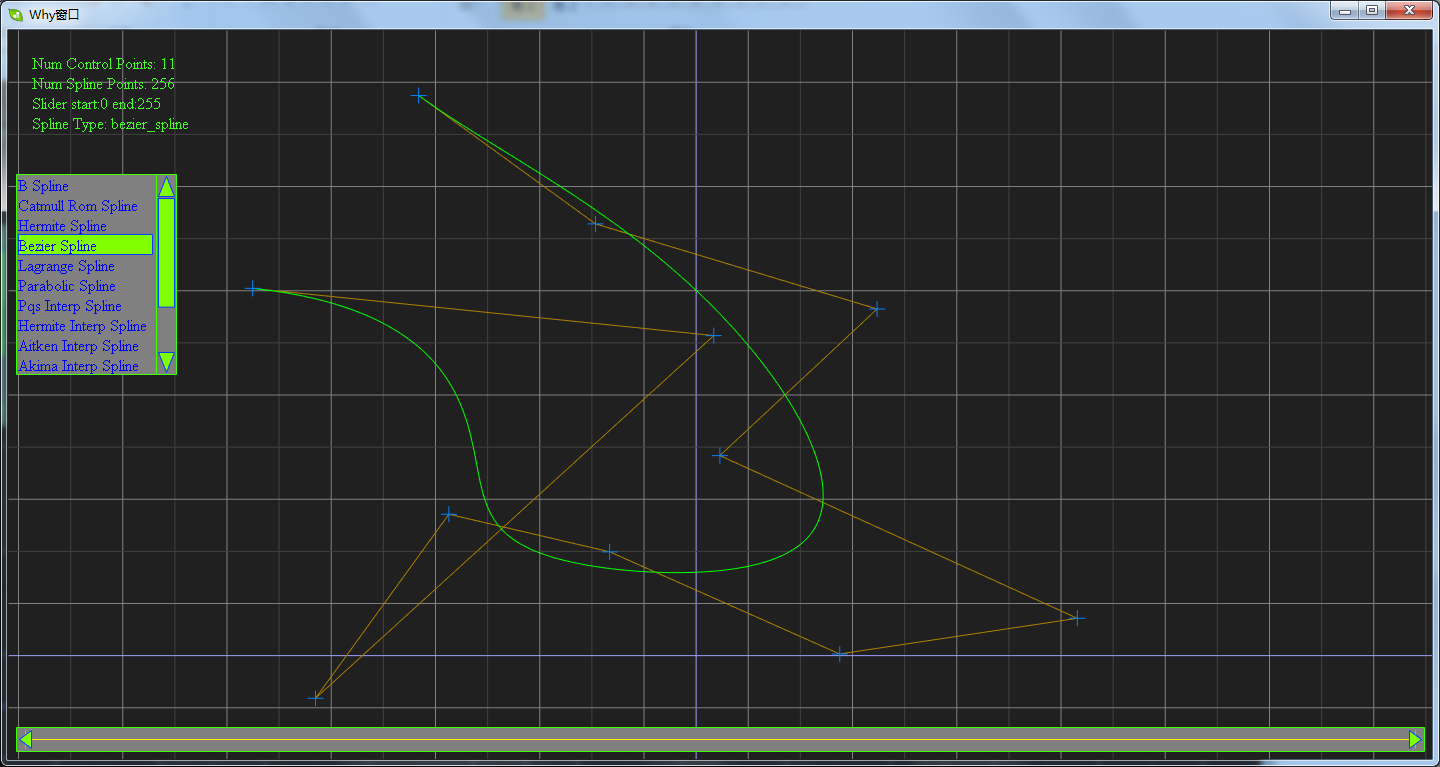
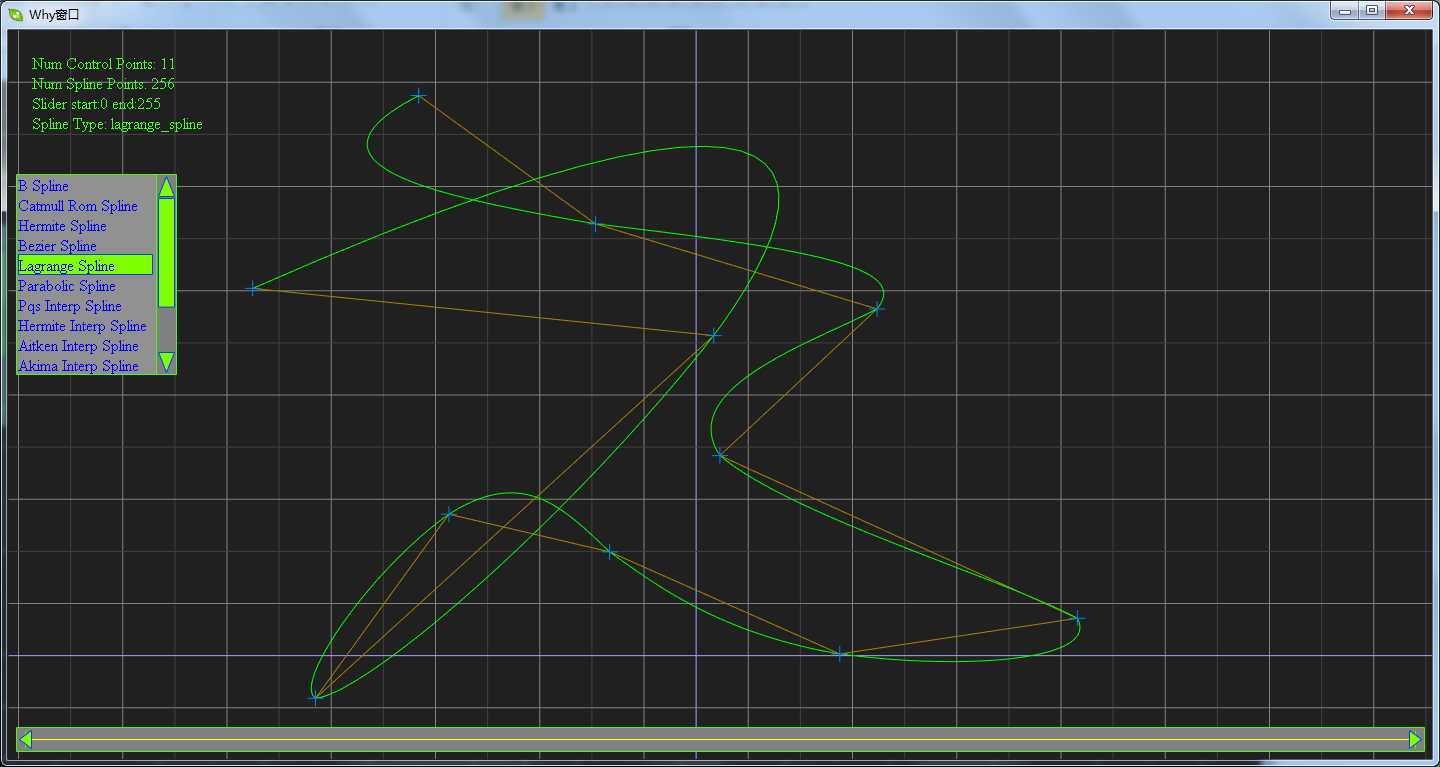
这是一个实现十余种样条曲线的程序DEMO。下载地址为:https://files.cnblogs.com/WhyEngine/TestSpline.zip
软件使用方式如下:
- 鼠标滚轮用于控制整个场景的缩放。
- 鼠标右键用于拖动场景。
- 按下CTRL并点击鼠标左键时,会添加一个采样点。
- 鼠标左键可以选中某一采样点。选中采样点后直接拖动鼠标可以修改其坐标位。如果选中采样点后按下CTRL再拖动鼠标可以插入一个新采样点。
- 选中采样点后按键盘DELETE可以删除采样点。
- CTRL + DELETE可以删除全部采样点。
- 通过界面左边的列表框,用于可以选择样条曲线的计算方式。
代码使用C++,开发环境为VS2008。所有的样条插值都是一个基类的子类:
/**************************************************************** File name : YicSpline.h Author : 叶峰 Version : 2.0 Create Date : 2014/08/18 Description : 样条 *****************************************************************/ #ifndef __YicSpline_H__ #define __YicSpline_H__ // INCLUDES ----------------------------------------------------------------------------- #include "..\WhyDefines.h" #include "..\WhyAssert.h" // -------------------------------------------------------------------------------------- class YicSpline { public: // 计算样条数值 virtual bool BuildSpline(const void* ctrlValuesPtr, Yuint ctrlStride, Yuint ctrlCount, void* splineValuesPtr, Yuint splineStride) const = NULL; // 计算切线数值 virtual bool BuildTangent(const void* ctrlValuesPtr, Yuint ctrlStride, Yuint ctrlCount, void* tangentValuesPtr, Yuint tangentStride) const { return false; } }; // -------------------------------------------------------------------------------------- inline float YfGetFloatValue(const void* valuesPtr, int stride, int index) { return *(float*)((char*)valuesPtr + stride*index); } // -------------------------------------------------------------------------------------- #endif
在下面的博客中,我会一一介绍这些样条的插值算法:
(2)样条之B

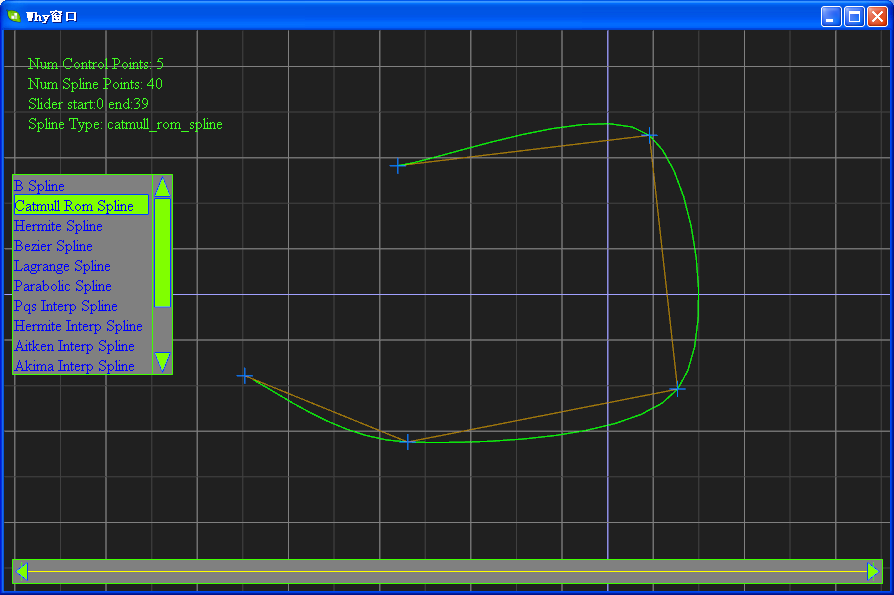



(7)样条之连分式插值函数
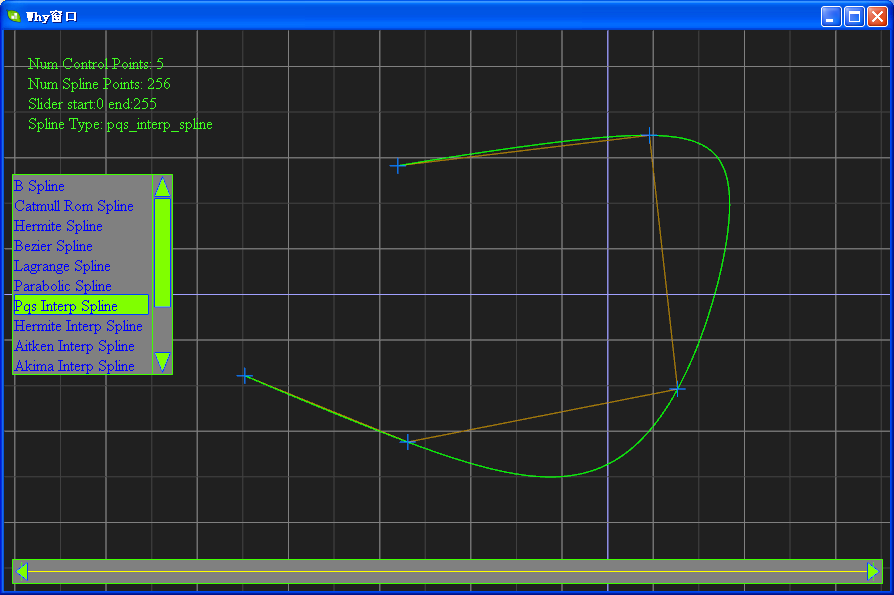



(10)样条之EHMT插值函数
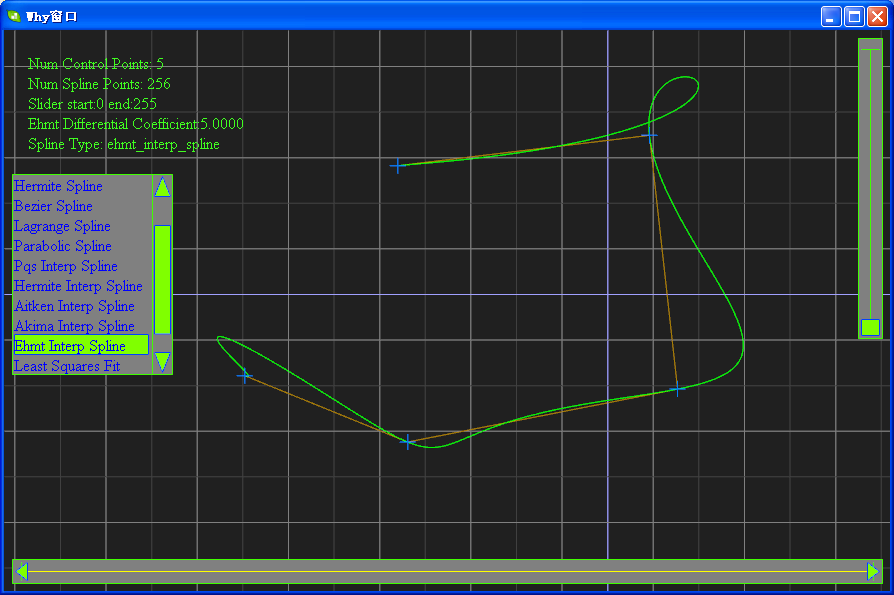
(11)样条之Akima光滑插值函数

(12)样条之最小二乘算法求多项式
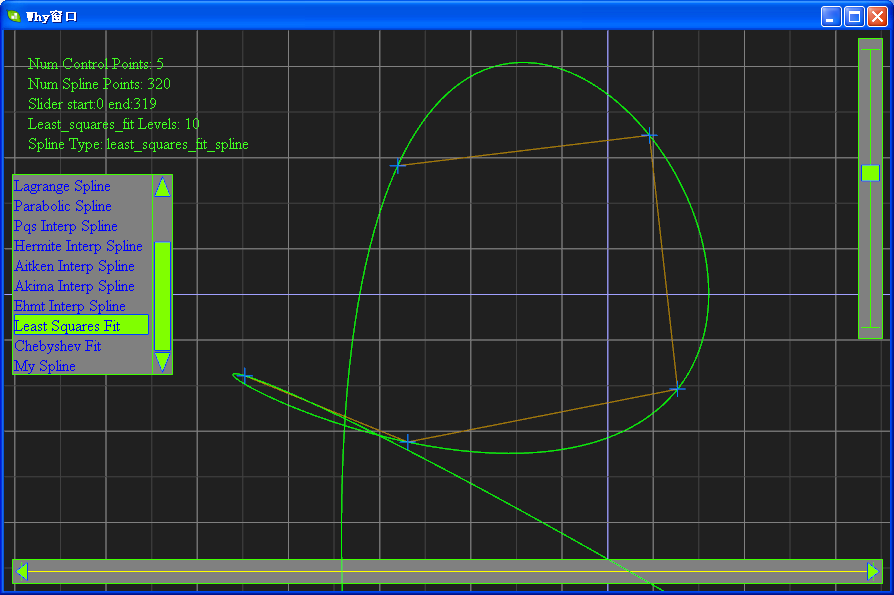
(13)样条之切比雪夫算法求多项式

最后转上一首诗,原址为:http://blog.sciencenet.cn/blog-39437-530669.html:
插值
有一种神奇叫简单美丽
有一种精彩叫数据处理
这是个十分古老的故事
故事主角不只厄米特伊
有一种拟合叫最小二乘
有一种插值叫拉格朗日
纠纠结结都是你情我愿
合合分分从来不伤和气
有一种苗条它叫做样条
有一种振荡它无止无息
钻之弥坚不必瞻前顾后
仰之弥高须从卑处做起
也许有些曲折有些失意
也许偶尔出轨偶尔迷离
这一切的一切都不重要
重要的是那过程和经历




 浙公网安备 33010602011771号
浙公网安备 33010602011771号