dp 优化合集
持续更新,技能树怎么一直都歪着点。
参考文章:
DP 的决策单调性优化总结 by command_block
1. 动态 dp
这玩意也能放到 dp 优化里面吗。
P4719 【模板】动态 DP
给定一棵树,点有权值,每次单点修改,求全局最大独立集。
\(n \leq 10^6,q \leq 3 \times 10^6\)
静态做法显然,设 \(f_{i,0/1}\) 表示以 \(i\) 为根的子树内 \(i\) 是否选择的最大独立集,显然有转移:
不妨考虑这个东西怎么做修改,为了迎合重链剖分的做法,我们设 \(g_{i,0}\) 表示 \(i\) 的轻儿子可取可不取的最大独立集,\(g_{i,1}\) 表示 \(i\) 的轻儿子全不取的最大独立集。
这种东西的思想或许跟 dsu on tree 类似,通过重剖的性质来均摊复杂度,改进之后我们有方程,令 \(j\) 为 \(i\) 的重儿子:
不妨将 \(g_{i,1}\) 与 \(a_i\) 合并,将其意义改为轻儿子全不取当前点必选的最大独立集,这样转移方程就与 \(a_i\) 无关。
关于 \(f_i\) 的区间维护,我们考虑类似做斐波那契时的想法,利用矩阵:
在斐波那契中,我们使用的是普通矩阵乘法,但在这里,涉及了 \(\max\) 运算,我们不如重新定义一下矩阵乘法,
新定义 \(\ast\) 运算符,\(A \ast B\) 的结果 \(C\),满足 \(C_{i,j} = \max_k(A_{i,k}+B_{k,j})\),当然这个东西是满足结合律的,感性理解就是因为加法和 \(\max\) 运算都满足结合律。
好的,我们此时发明了广义矩阵乘法,类似矩阵快速幂的来构造关系矩阵,令关系矩阵为 \(U\):
简单手模一下就能得到,转移应为:
好了,到这里我们就已经发明了 ddp,维护时,这玩意好像不是很满足交换律,所以线段树维护时是从左到右维护,把转移转过来就好了:
因为我们的定义很特殊,所以对于一个重链的链头的答案显然是整条重链的矩阵乘积,因此我们还需要每条重链的开头结尾。
修改时,因为每到链头向上跳的时候就不是重儿子了,所以链头父亲的关系矩阵需要改变,将原贡献减掉再加上新贡献就好了,好了,做完。
复杂度 \(O(2^3 n\log^2 n)\)。
加强版其实双 log 也可以草过去的,只不过需要卡一卡常,比方说用前向星存图,改成对每条重链开动态开点线段树,能省去几个查询时的 log,优化还是比较明显的。
正常版: Submission
卡常版,通过了加强版,注意 _unlocked 在本地不过编。
P5024 [NOIP 2018 提高组] 保卫王国
已知最小点覆盖 = 全集 - 最大独立集,转成模版题就做完了,对于必须选和不能选,改一下 \(a_i\) 的取值就好了。
P7359 「JZOI-1」旅行
给定一棵树,边有向且有权,造船需 \(L\) 的时间,坐船顺走边权为 \(a_i - z_i\),逆向走边权为 \(a_i + z_i\),不坐船边权为定值 \(L\),\(q\) 组询问,回答 \(u,v\) 之间最短路。
\(1 \le n,q \le 2\times 10^5,0 \le a_i,L \le 10^5\)。
怎么把几个做法拼起来了。
考虑单组怎么做,换一下根,然后设 \(f_{i,0/1}\) 表示第 \(i\) 个点当前有没有船即可。
这个转移很简单,而我们需要支持快速合并链,考虑套上矩阵,更具体地,我们对每一条链定义:
- \(a\) 这条链进出时都没船
- \(b\) 这条链进入之前有船,出链前没船。
- \(c\) 这条链进入之前没船,出链前有船。
- \(d\) 这条链进入时就有船,出链前还有船。
注意此处定义进入时有船是其之前的链造过船了,而不是在这条链进入后再造船,所以答案统计处不应带上 \(b,d\),同理,定义是在出链前有船,则在最后链中最后一条边前造过船了,所以 \(c,d\) 的初值应该是坐船的。
根据含义容易写出合并。其实此处合并就是原 dp 转移矩阵的 \((\min,+)\) 矩阵乘法。
因为没有修改,所以不需要线段树,倍增维护即可,注意要维护两个方向进出的矩阵,复杂度 \(O(n\log n)\)。
P6573 [BalticOI 2017] Toll
给定 \(n\) 个点 \(m\) 条边的有向图,\(q\) 次询问任意两点之间最短路,保证每条边 $u < v $ 且 \(u+k > v\)。
\(1 \le n,m \le 5\times 10^4, 1\le q \le 10^4,1 \le k \le 5\)。
很厉害的题。
注意到这个性质给的 \(k\) 很小,能够发现整张图其实是 \(\lfloor \frac{n}{k} \rfloor\) 层的分层图,且只有相邻两层有边相连,考虑维护两层之前的转移矩阵线段树暴力维护转移即可。
但是,考虑到转移矩阵是 \((\min,+)\) 矩阵乘法,且可以用倍增平替线段树,于是我们考虑 Floyd + 倍增暴力维护转移矩阵,即 \(f_{i,a,b,j}\) 表示第 \(i\) 层的第 \(a\) 个点到第 \(i + 2^j\) 层的第 \(j\) 个点的最短路。
暴力维护即可做到 \(O(k^3n\log n)\),分治可以再少一个 \(k\),有一点卡空间。
2. 矩阵快速幂优化
额,有几个好题,就写一下这个。
板子不讲了,注意有的时候可以用向量乘矩阵。
CF576D Flights for Regular Customers
给定一张有向图,每条边有权 \(d_i\),表示经过这条边前至少需经过 \(d_i\) 条边,求 \(1\) 到 \(n\) 的最短路。
\(1 \le n,m \le 150,1 \le d_i \le 10^9\)。
好题啊。
考虑将边按 \(d_i\) 排序,我们需要在加入每一条边时维护连通性,将当前连通性记作矩阵 \(A\),图边联通性记作矩阵 \(B\),那么对于一段没加边的时间 \((l+1,d_i]\),我们只需要令 \(A \gets A \times B^{d_i-l}\) 即可。
然后直接对 \(B\) 进行修改,注意此时不能将 \(A\) 矩阵内的连通性当作最终答案,因为 \(n\) 可能早就跑到了,于是每一次加边之后我们进行一次 bfs,找出最短路再进行下次更新即可,复杂度 \(O(n^3m\log n)\),无法通过。
注意到联通性是一个 \((\text{OR},\text{AND})\) 矩阵乘法,所以可以使用 bitset 维护转移,复杂度变为 \(O(\frac{n^3m\log n}{w})\)。
P1707 刷题比赛
给了三个线性转移式,求第 \(n\) 项的和。
\(1 \le n \le 10^16\)。
显然矩阵快速幂,但是矩阵太大了。
答案矩阵即:
转移矩阵是:
直接做就好了。
P2151 [SDOI2009] HH 去散步
给定一张无向图,每一秒走一条边,不能走前一秒走过的,求 \(a\) 到 \(b\) 恰好用 \(t\) 秒的路径数。
\(1 \le n \le 50,1 \le m \le 60,1 \le t \le 2^{30}\)。
不能走上一步走过的边,那么我直接设 \(f_{i,j}\) 为第 \(j\) 秒走到 \(i\) 点就不行了,改一下状态,\(f_{i,j}\) 表示第 \(j-1\) 秒走的是第 \(i\) 条边的方案数,因为边很少,直接转移即可,复杂度 \(O(m^3\log t)\)。
3. 斜率优化
暂时参考了 这个博客。
3.1. 算法简介
从一个最简单的转移优化写起,比方说有方程 \(f_i = \min \limits_{1\leq j < i} \{ g_j + a(i) + b(j)\}\),其中 \(a(i),b(j)\) 是两个分别只关于 \(i,j\) 的代价函数。
那么显然我们 \(a(i)\) 对每一个 \(g_j + b(j)\) 的贡献都是相同的,因此,我们可以把 \(a(i)\) 提出来,写作 \(f_i = \min \limits_{1 \leq j < i} \{ g_j + b(j)\} + a(i)\)。
然后我们只需要记录 \(minx\) 为 \(g_j + b(j)\) 的最小值,转移为 \(f_i = minx + a(i)\) 就可以做到 \(O(1)\) 转移了。
进一步的,我们如果有转移 \(f_i = \min \limits_{1 \leq j \leq i} \{ g_j + a(j) + b(i)c(j)\}\),就不能通过一次找 \(\min\) 来寻找最优决策点 \(j\) 了,我们此时就有很多种方法来处理这个东西了,比如李超树,决策单调性,斜率优化等等,这里要说的就是斜率优化。
Print Article
给定 \(n\) 个位置,每个位置有代价,分成任意段,每一段的代价为 \((\sum \limits_{i=l}^r a_i )^2 + m\),求分段最小代价。
从这题入手,详细写一写,首先容易写出方程,\(f_i = \min \limits_{0\leq j < i} \{ f_j + (s_i - s_j)^2 + m\}\),其中 \(s_i\) 表示前缀和。
我们先不考虑 \(\min\),将其拆开,得到 \(f_i = f_j + s_i^2 + s_j^2 - 2s_is_j + m\)。
移项,得 \(f_j + s_j^2 = 2s_is_j - s_i^2 + f_i - m\),我们令 \(y = f_j + s_j^2\),\(k = 2s_i\),\(x=s_j\),\(b=-s_i^2 + f_i -m\),就能够得到形如 \(y=kx + b\),的直线方程,不如放到平面坐标系上考虑,我们只要令直线的截距最小,由于 \(-s_i^2 + m\) 可以认为是常值,那我们 \(f_i\) 就可以取到最小值,而且这种情况下我们的斜率是已知的,就为 \(2s_i\),放个图。
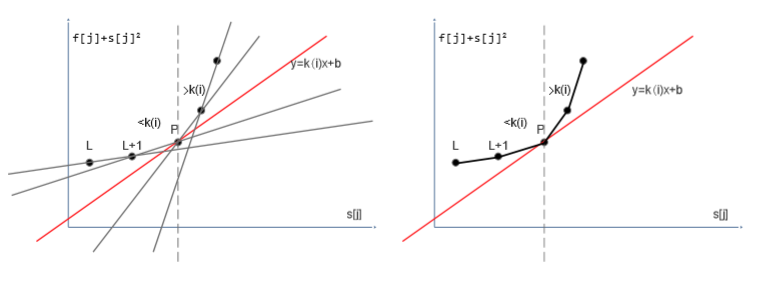
这个坐标系是以 \(s_j\) 为横轴,\(f_j + s_j^2\) 建立的,由于前缀和是单调的,也就是说我们每一次查找的斜率 \(2s_i\) 是单调的。当图上相邻两点的斜率 \(< k\) 时,显然前一个点对答案是肯定没有贡献的,因为我们完全可以选择 \(x\) 更大的点来使截距变小,因此,我们只需要保留相邻两点斜率 \(>k\) 即可,而且要保证斜率单调递增,这个也跟上面一样,画画图就很好理解了。
那么,这题我们完全可以用单调队列来维护这个斜率单调递增的下凸包,每次取队首就是最优决策点,如图中就是画虚线经过的点。
但是,在某些题中,我们的 \(k\) 可能并不递增,所以我们需要在下凸包上二分来寻找答案了,也就是队列二分。
同理,假设给本题加上了分正好 \(m\) 段的代价,我们只需要再套一个 wqs 二分再求答案即可。
注意队列顺序和队列下标。
任务安排
\(n\) 个任务等待完成。从时刻0开始,这些任务被分批加工,第 \(i\) 个任务所需时间 \(t_i\)。每批任务机器需要启动时间 \(s\),同一批任务将在同一时刻完成。每个任务的费用是它的完成时刻乘以一个费用系数 \(f_i\),求最小费用。
这题有三个版本,我们依次讲起。
考虑暴力转移,由于每次我们不好确定当前这一段开始前的时间,放到状态上也不合适,所以我们考虑每次新增 \(s\) 时,显然会对后面所有任务产生贡献,这个贡献很好计算,记个前缀和就好了,这样,我们不考虑分段带来的额外时间,每一段的时间也就固定了。
考虑设 \(f_i\) 表示前 \(i\) 个任务的最小代价,那么有转移 \(f_i = \min \limits_{0\leq j < i} \{ f_j + pf_i(pt_i - pt_j) + s(pt_n - pt_j)\}\),转移 \(O(n)\),总复杂度 \(O(n^2)\),其中 \(pt_i\) 和 \(pf_i\) 分别表示 \(t\) 和 \(f\) 的前缀和。
考虑进一步优化,我们发现上面这个式子完全可以类似斜率优化的展开,然后直接斜率优化即可,复杂度 \(O(n)\),可以通过加强版。
考虑进一步加强版,假设我们令 \(|t_i| \leq 10^7\),那我们每一次的斜率 \(pt_i\) 就不单调递增了,那我们就不能每次取队头了。重新考虑一下,由于斜率单调,每次取斜率 \(\geq k\) 的点肯定最优,所以我们使用单调队列来维护,但是斜率不单调后,我们只要维护这个下凸包,还是可以二分找到最优决策点的,这也就是队列二分,复杂度 \(O(n\log n)\),可以通过加加强版。
注意不能将队头出队。
Bear and Bowling 4
在一个长 \(n\) 的序列中选出一个连续子段,使得 \(\sum \limits_{i=1}^k i a_i\) 最大,求最大值。
\(1 \leq n \leq 2\times 10^5,|a_i| \leq 10^7\)。
简单题,不妨考虑 \(f_i\) 表示以第 \(i\) 个点为右端点的最大答案,那么有 \(f_i = \max \limits_{0\leq j < i}\{ p1_i - p1_j - j(p2_i - p2_j) \}\),其中 \(p1_i = \sum ia_i\),\(p2_i = \sum a_i\),然后拆成直线方程的样子就好了。
主要是拿这题说一下细节问题,一个是可能拆开之后发现你的 \(x\) 不是单调的,这样的话斜率优化就假完了,所以需要变换一下形式,包括队列二分的写法,一定不要写错,见代码。
以及上凸包的维护方法,和下凸包全部反过来就好了。
P14186 [USACO08MAR] Land Acquisition G(数据加强版)
给定 \(n\) 个二元组 \((a_i,b_i)\),规定一个子集的代价为 \(a_i\) 与 \(b_i\) 最大值的乘积,求划分最小代价。
\(1 \le n \le 2\times 10^5,1 \le V \le 10^6\)。
怎么被一眼秒了。
由于是子集划分,我们不好直接 dp,考虑能否通过某些手段使其变为区间划分。
首先显然,对于一对 \(a_i \ge a_j \wedge b_i \ge b_j\),\(j\) 肯定可以划分到 \(i\) 的集合内从而不带来代价,我们直接把 \(j\) 删掉即可。
那么,我们对 \(a_i\) 排序,则在 \(b\) 中,存在 \(j\) 满足 \(i < j \wedge b_i \le b_j\) 的 \(i\) 一定无用,我们将其删掉,进一步地,最终的 \(b\) 序列一定单调递减。
那么,由于 \(a,b\) 都有单调性了,我们的选择就一定是一个区间了,因为如果跳着选的话,跳过去的数一定可以划分到这个集合内从而不带来代价。
然后就可以写出转移了,设 \(f_i\) 表示到第 \(i\) 个位置的最小代价,则有转移:
暴力转移是 \(O(n^2)\) 的,直接斜率优化即可,复杂度 \(O(n\log n)\)。
CF1715E Long Way Home
一张图,边有边权,拥有 \(k\) 次跳跃机会,一次跳跃的代价是 \((u-v)^2\),\(u,v\) 分别表示起点重点的编号,求 \(1\) 到所有点的最短路。
\(1 \leq n,m \leq 10^5,1 \leq k \leq 20,1 \leq w \leq 10^9\)
简单题。
发现 \((u-v)^2\) 不好通过构造某些奇怪的边权实现,但是 \(k \leq 20\),我们不妨将每一个次跳跃单独拿出来做,找出了最优的跳跃位置再重新跑最短路,dij 实现的复杂度是 \(O(k(n+m)\log n)\) 的。
考虑如何求最优跳跃位置,不妨 dp,为了与最短路适配,设 \(f_i\) 表示 \(1\) 到 \(i\) 的最短路长度,那么有转移 \(f_i = \min \limits_{j=1}^n f_j + (i-j)^2\),发现这很斜率优化,然后套路拆一下式子得到,\(f_j + j^2 = f_i-i^2+2ij\),令 \(k=2i\),\(x=j\),\(y=f_j+j^2\),直接套斜优即可,复杂度 \(O(nk)\)。
把这两步套起来,注意转移时要新开数组,复杂度 \(O(k(n+m)\log n)\)。
CF1179D Fedor Runs for President
一棵树,新增一条边,使得简单路径的数量最多,求最多路径条数。
\(1 \leq n \leq 5\times 10^5\)。
超级好题,一开始确实考虑少了,再推几步应该就能出来了。
加边之前,树的路径条数为 \(\frac{n(n-1)}{2}\),这个在加边之后数量不会变,所以我们只需要考虑加边带来的新增路径条数就好了。
给一张图:
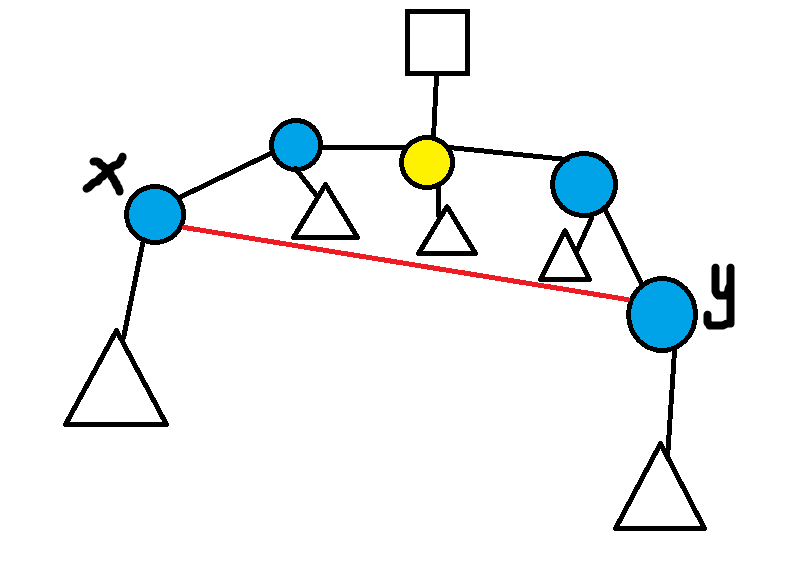
图中,红色边为我们假定的新增边,其两端分别为 \((x,y)\),黄色点为这一棵子树的根,正方形为其祖先,所有三角形为该点下挂的子树,圆点就代表这一个点。
我们只考虑这条链上的点,记 \(P(x,y)\) 表示这条链,\(s_x\) 为以 \(x\) 为根,不向链上扩展的子树大小,对于蓝色点,\(s_x\) 即为三角形大小加上它自己,对于黄点,需要再多加正方形的大小。
那么这样,答案为 \(\frac{\sum_{i\in P(x,y)}s_i(n-s_i)}{2}\),这个很好理解,取链上一点 \(i\),\(s_i\) 内的点不能互相有过新边的路径,根据乘法原理,这一些点对总答案的贡献就是 \(s_i (n-s_i)\)。
补:这里可能会有疑惑,因为上面是按照 \(x,y\) 不是祖先关系来的,考虑当 \(x\) 为 \(y\) 的祖先时,这个式子不变,只是 \(n-s_i\) 变成了链外点,然后 \(s_i\) 就是链中点,当然此时 \(s_i\) 的含义就是子树大小,而式子是不变的,所以我们只需要按照 \(x,y\) 不是祖先关系来做就好了。
将这个式子简单拆一下 \(\frac{\sum_{i\in P(x,y)}s_i(n-s_i)}{2} = \frac{n\sum_{i\in P(x,y)}s_i - \sum_{i\in P(x,y)} s_i^2}{2}\),然后 \(\sum s_i\) 其实就是 \(n\),所以答案为 \(\frac{n^2 - \sum_{i\in P(x,y)}s_i^2}{2}\),考虑让答案最大,即让 \(\sum s_i^2\) 最小,这样我们将问题转化为求一条路径,使得 \(\sum s_i^2\) 最小。
对于这样的路径问题,我们的常用做法是按子树处理再合并,不妨设 \(f_i\) 表示以 \(i\) 为根的子树内,一条蓝点链以 \(i\) 为一端的最小贡献,转移即 \(f_i = \min \limits_{j \in son(i)} \{f_j + (siz_i - siz_j)^2\}\),其中 \(siz_i - siz_j\) 即为 \(i\) 点的 \(s_i\)。
然后考虑合并,\(ans = \min \limits_{y \in son(x),z\in son(x),y\neq z} \{ f_y + f_z + (n-siz_y - siz_z)^2\}\),此时,\(x\) 点即为这一条链的黄点,所以其 \(s_x\) 为 \(n-siz_y -siz_z\),这也解释了为什么 \(f_i\) 的含义是蓝点链了。
至此,我们已经有了 \(O(n)\) 答案转移的方法了,考虑优化,这个式子显然是可以做斜率优化的。
我们枚举 \(y\),将这个式子拆开,写作 \(ans-f_y+(n-siz_y)^2 + 2siz_z(n-siz_y) = f_z + siz_z^2\),然后令 \(Y=f_z + siz^2\),\(K=2(n-siz_y)\),\(X=siz_z\),然后维护一个下凸包就好了,发现 \(X,Y\) 均单调,所以用单调队列维护就好了,前提是按照 \(siz_i\) 排序,这样的话瓶颈在于每一个点对儿子的排序,发现每一个点只会被排序一次,所以总复杂度 \(O(n\log n)\),可以通过。
注意算上当前 \(x\) 就是链的结尾的答案,也就是 \(ans = \min \limits_{y \in son(x)} \{ f_y + (n-siz_x + siz_x -siy)^2\}\),也就是算上 \(f_y + (n-siz_y)^2\)。
CF311B Cats Transport
\(m\) 只猫,\(p\) 个饲养员,\(n\) 座山。第 \(i\) 到第 \(i-1\) 座山之间的距离为 \(d_i\)。 第 \(i\) 只猫去 \(h_i\) 号山玩,玩到 \(t_i\) 停止,开始等待饲养员。 规划每个饲养员从 \(1\) 号山出发的时间,使得所有猫等待时间总和最小。
\(1 \leq n,m \leq 10^5,1 \leq p \leq 100,0 \leq t_i \leq 10^4\)。
很巧的转化题,我竟然手撕了 *2400。
由于是斜率优化题单里面的,所以往 1D1D 的东西那边想一想,发现我们每一轮都只能拿掉一部分点,而且这些点还不连续,不妨考虑一个贪心的思路,对于每只猫,由于饲养员在路上是不停的,所以我们可以算出恰好经过一只猫的起始时间是 \(T_i - \sum \limits_{j=1}^{H_i} D_j\),记作 \(P_i\),那么我们直接按照 \(P_i\) 从小到大来选点肯定就是最优的了,这个很好证明吧,邻项交换一下。
之后,我们将问题转化成,这个 \(m\) 只猫,至多分成连续的 \(p\) 段,最小代价是多少,这个就是很典的斜率优化了,考虑 \(f_{i,k}\) 表示前 \(i\) 只猫,分了 \(k\) 段的最小代价,然后有转移 \(f_{i,k} = \min \limits_{0 \leq j < i} \{ f_{j,k-1} + w(i,j)\}\),这里 \(w(i,j)\) 还要再仔细算一下,因为我们按照 \(P_i\) 排序,所以 \(P_i\) 就是我们的起始时间,而每一个点的位置是不同的,所以代价是 \(\sum_{k} (P_i - T_k + \sum \limits_{j=1}^{H_k} D_j)\),把这个式子直接拆开做斜率优化就好了,复杂度 \(O(np)\)。
CF643C Levels and Regions
对于一个 \(j\),如果其所在连续段以 \(i\) 为开头,记 \(s = \sum \limits_{k=i}^j t_k\),那么其一次通关的概率是 \(\frac{t_j}{s}\),期望时间为 \(\frac{s}{t_j}\)。
对一个连续段,每个关卡一定是顺着通关的,这样我们就可以考虑 dp 了。
不考虑分段的限制,设 \(f_{i}\) 表示通关 \(i\) 所需的最小时间,那么有转移:
令 \(s_i = \sum \limits_{j=1}^i t_j\),则有:
然后令 \(a_i = \sum \limits_{j=1}^i \frac{s_i}{t_i}\),\(b_i = \sum \limits_{j=1}^i \frac{1}{t_i}\),就可以写作:
就可以做到 \(O(1)\) 转移了,然后还需要加上段数限制,这样的复杂度是 \(O(n^2k)\) 的。
优化的话可以考虑证明其代价函数的四边形不等式,从而得出决策单调性,然后做决策单调性分治,复杂度 \(O(nk\log n)\),或者说注意到代价函数与 \(i,j\) 都有关的只有 \(s_jb_i\) 这一项,套用斜率优化即可,复杂度 \(O(nk)\)。
注意一下实现时的精度。
CF1083E The Fair Nut and Rectangles
由于矩形不包含,于是我们将点按照 \(x_i\) 排序后,\(y_i\) 一定是降序排列,那么就可以写出 dp 式子,设 \(f_i\) 表示前 \(i\) 个矩形的最大值:
发现这是斜率优化形式,将原式写作 \(f_j = x_jy_i + f_i - x_iy_i + a_i\),然后令 \(y = f_j,k=y_i,x=x_j,b = f_i-x_iy_i +a_i\),斜率和横坐标都单调,于是单调队列维护一个上凸包即可,复杂度 \(O(n)\)。
P4027 [NOI2007] 货币兑换
容易写出,当一天的收益为 \(f_i\),那么能够买的 \(A\) 券数为 \(x_i = \frac{f_ir_i}{a_ir_i + b_i}\),\(B\) 券数为 \(y_i = \frac{f_i}{a_ir_i+b_i}\),然后转移为 \(f_i = \max \{ a_ix_j + b_iy_j\}\),发现是齐次的,移项之后斜率优化即可,因为坐标和斜率不单调,用李超树,复杂度 \(O(n\log n)\),看了第一篇题解的实现,这么短的李超树写的真的很好。
4. 带权二分
即 wqs 二分,往往对于 2D/1D 具有凸性的 dp 使用,如序列分段。可将 2D/1D 的 dp 通过二分变为 \(\log V\) 个 1D/1D 的 dp,常配合斜率优化,决策单调性等使用。
常见的 wqs 问题形如恰好选 \(k\) 个的问题,因为一般很明显,所以比较套路。
当然 wqs 的优化基于原问题有凸性,或者代价函数满足四边形不等式,场上可以直接猜测或者打表,建立费用流模型来证明原问题凸性。
4.1. 算法简介
偷一张图。
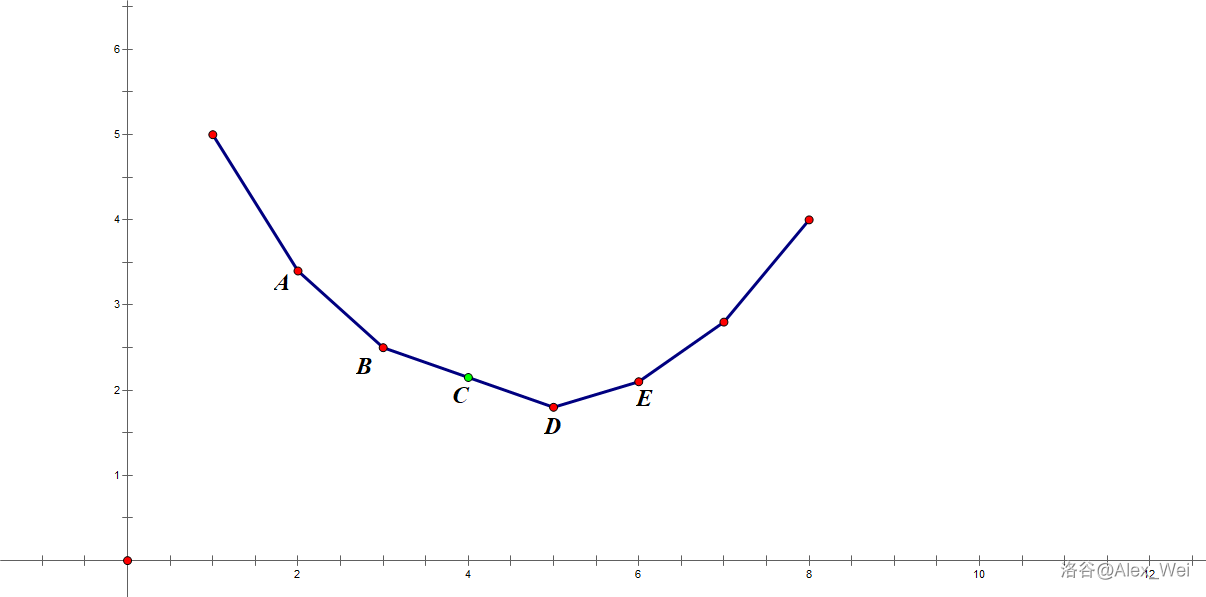
此处纵轴一般为问题答案,横轴为限制的物品数量,wqs 一般是直接二分斜率去卡点,而因为已知斜率和过点,就可以反推截距,得到原问题答案,这也说明了为什么 wqs 最后减去多余贡献的时候是 \(-mk\) 了。
通过 wqs 二分,我们为每一次新选物品带权,将问题转化为 1D/1D 的 dp,只需要在 dp 过程中记录物品个数反推交点即可,通常复杂度为 \(O(n\log V)\)。
一般问题中,wqs 的斜率为整数,而某些特殊问题中,我们需要实数二分,这时为了保证复杂度,就要限制二分次数了。
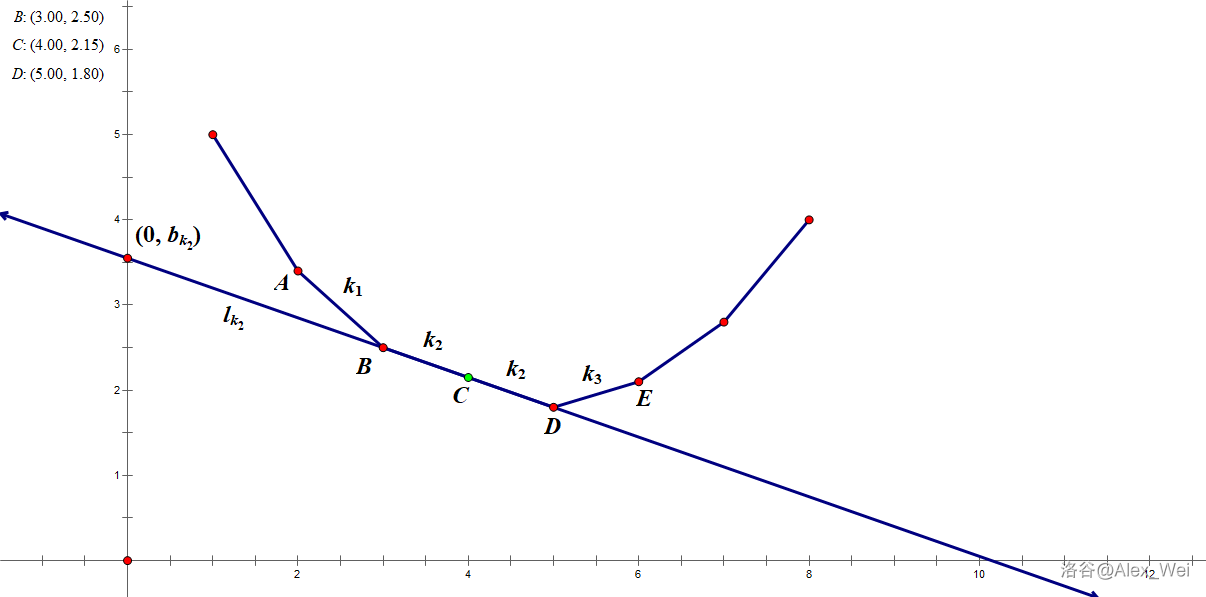
然后要特别讲一下三点共线的情况,这也是 wqs 最容易出问题的地方。
以求 \(\min\) 为例,上图中,当我们斜率等于 \(k_3\) 时,卡到的是 \(D\) 点,此时 \(D\) 一定不是我们的答案,当斜率等于 \(k_2\) 时,卡到 \(B\) 点,\(B\) 此时可能是我们的答案,因此,对于最小化时,应令 r=mid-1,l=mid,mid=l+r+1>>1。
求 \(\max\) 时同理,将 \(l,r\) 颠倒即可,注意此处讨论的是下凸包,上凸包还要重新讨论。
还有一些 1D/1D dp 的实现问题,放到题目里面一块说吧。
P5633 最小度限制生成树
给定一带权无向图,限制 \(s\) 点需恰好链接 \(k\) 条边,求最小生成树。
\(1 \le n \le 5\times 10^4,1 \le m \le 5\times 10^5\)。
对于凸性不作证明,感性理解一下。
因为有凸性,考虑 wqs 二分,对所有与 \(s\) 相连的点加权即可,注意实现时,如果让斜率尽可能小,则要在对边排序时将与 \(s\) 相连的边向后放,其余与 Kruskal 无异,注意最后减去的是 \(kl\)。
CF739E Gosha is hunting
有 \(n\) 个精灵,有 \(a\) 个精灵球,\(b\) 个大师球,每个精灵球有 \(c_i\) 的概率捕捉,每个大师球有 \(d_i\) 的概率捕捉,一只精灵可以同时使用两个球,求最大期望捕捉精灵数。
\(1 \le n \le 2000\),误差不超过 \(10^{-4}\)。
显然有 dp,设 \(f_{i,j,k}\) 表示前 \(i\) 只精灵,用了 \(j\) 个普通球,\(k\) 个大师球的最大期望,转移很简单,复杂度 \(O(n^3)\)。
考虑优化,不难猜想 \(f_{i,j,k}\) 的后两维均具有凸性,其实可以二维 \(wqs\) 直接做到 \(O(n\log^2 n)\),但是写完发现误差太大了,于是只用一维就可以了。
5. 决策单调性:分治
常用于 2D/1D 的 dp 优化,而且要求一维是层数,而且必须是相邻层数之间的转移。
决策单调性是一个很优秀的性质,我们有许多方法来优化具有决策单调性的 dp,而决策单调性一般是体现在 1D 维度上的,设 \(f_i\) 表示当前层,\(g_i\) 表示上一层,那么对于 \(f_i\) 从 \(g_{p_i}\) 转移,则有如果 \(j>i\),那么 \(p_j \ge p_i\)。
5.0. 四边形不等式
对于一个 1D/1D 的 dp 来说,其转移式子一般可以写为 \(f_i = f_j + w(i,j)\),如果 \(w(i,j)\) 满足四边形不等式,那么 \(f\) 具有决策单调性。
四边形不等式,即包含劣于相交,假设我们要最小化 \(f\),那么 \(w(i,j)\) 需对于任意 \(a < b < c < d\),满足 \(w(a,d) + w(b,c) \le w(a,c) + w(b,d)\),因为这个不等式可以被刻画为平面上一个平行四边形,于是被称为四边形不等式。
然后我们来证明为什么 \(w(l,r)\) 满足四边形不等式,则 \(f\) 具有决策单调性,考虑反证法,假设存在 \(p_j < p_i < i < j\),因为 \(p\) 是最小的决策点,此时要代价最小,那么有:
两式相加可以得到:
由于此时满足四边形不等式,所以有 \(w(p_j,i) + w(p_i,j) \le w(p_j,j) + w(p_i,i)\),对于 \(w(p_j,i) + w(p_i,j) < w(p_j,j) + w(p_i,i)\),与上式矛盾,对于 \(w(p_j,i) + w(p_i,j) = w(p_j,j) + w(p_i,i)\),由于此时 \(p_i = p_j\),与 \(p_i\) 的最小性矛盾,假设不成立,证毕。
其实大多数时候都只是猜测满足四边形不等式的。
5.1. 算法简介
然后来说如何根据决策单调性分治优化 dp。
因为相邻两层之间的转移是满足决策单调性的,于是我们可以每次选取区间中点 \(m\) 并暴力求出 \(m\) 的答案及最优决策点 \(p_m\),注意需满足 \(p_m \le m\),然后递归处理 \([l,m)\) 和 \((m,r]\),用 \(p_m\) 来缩小每个区间的决策范围,类似整体二分的思路。
对于 \([l,m)\),其决策范围为 \([pl,p_m]\),对于 \((m,r]\),其决策范围为 \([p_m,pr]\),这样递归只有 \(O(\log n)\) 层,每层只需要便利 \(O(n)\) 次,所以复杂度 \(O(n\log n)\)。
\(k\) 层的话就暴力记录上一层答案,然后再跑一遍分治即可,复杂度 \(O(nk\log n)\)。
5.2. 贡献难算
有些时候,\(w(l,r)\) 我们不好 \(O(1)\) 快速计算,但是我们可以快速将 \(w(l,r)\) 推到 \(w(l-1,r)\) 或者 \(w(l,r+1)\),一次扩展时间为 \(O(t)\),那么决策单调性依旧可以做到 \(O(nt\log n)\),即端点的移动总次数只有 \(O(n\log n)\),类比莫队的查询,每一次暴力移动左右端点。
考虑分析这个复杂度:
-
对于右端点,它是区间中点,所以只会是从 \(l\) 走到 \(m\),或者从 \(r\) 走到 \(m\),只会有 \(O(n)\) 次移动。
-
对于左端点,它是每一次的决策点,在进入 \([l,m)\) 和 \((m,r]\) 中时,移动次数是 \(pr-pl\) 级别的,也只有 \(O(n)\)。
于是,指针的总移动次数只有 \(O(n\log n)\),总复杂度只有 \(O(nv\log n)\)。
P4360 [CEOI 2004] 锯木厂选址
给定 \(n\) 个点,每个点有权重 \(w_i\),到下个点的距离 \(d_i\),初始只有 \(n+1\) 为终止点,走 \(d_i\) 距离的答案是 \(d_iw_i\),求再放置两个终止点的最小代价。
\(1 \le n \le 2\times 10^4\)。
不难写出两个点之间的代价函数 \(\text{cost}(i,j)\),考虑设 \(f_i\) 表示在 \(i\) 放置第二个终止点的最小代价,容易处理出在第 \(i\) 个位置放第一个中转点的代价 \(v_i\),于是有转移:
直接转移是 \(O(n^2)\) 的,考虑进一步优化,对于代价函数 \(w(l,r)\),其要满足四边形不等式,当且仅当:
即:
即对于函数 \(f_l(r) = w(l,r) - w(l-1,r)\) 单调不减,显然 \(w(l,r)\) 随 \(r\) 的增大而增大,于是原函数满足四边形不等式,即 dp 具有决策单调性,分治优化转移即可。
CF868F Yet Another Minimization Problem
给定长 \(n\) 的序列,一个子段的代价定义为相同元素对数,求将序列分为 \(k\) 段的最小代价。
\(1 \le n \le 10^5,1 \le k \le \min(n,20)\)。
不妨设 \(f_{i,j}\) 表示到第 \(i\) 个位置,划分了 \(j\) 段的最小代价,那么有转移:
现在有两个问题,一个是 \(w(k+1,i)\) 的预处理是 \(O(n^2)\) 的,一个是原 dp 是 \(O(n^2k)\) 的。
其实能够注意到,\(w(l,r)\) 应该是满足四边形不等式的,因为包含的大区间两端会多算,而交叉的没有,于是原 dp 满足决策单调性。
这样我们可以通过分治将 dp 优化到 \(O(nk\log n)\),但是 \(w(l,r)\) 的计算还是 \(O(n^2)\) 的,考虑莫队式指针移动,根据结论,所有 \(w\) 的计算是 \(O(n\log n)\) 的。
于是,复杂度为 \(O(nk\log n)\)。
P5574 [CmdOI2019] 任务分配问题
同上题,子段的代价为顺序对个数,序列为排列。
\(1 \le n \le 2.5\times 10^4,1 \le k \le 25\)。
这俩题真一样吧,将用莫队数顺序对就好了,复杂度 \(O(nk\log^2 n)\),证明也基本一样,好像这题可以 wqs 二分了。
P6173 [USACO16FEB] Circular Barn P
首先断环为链,那么我们需要对 \(n\) 个序列 dp。
考虑设 \(f_{i,k}\) 表示到第 \(i\) 个位置,建了 \(k\) 个谷仓的最小移动距离,那么有转移:
其中 \(w(l,r) = \sum \limits_{i=l}^r a_i(i-l)\),\(w(l,r)\) 容易通过预处理前缀和 \(O(1)\) 计算,那么上述 dp 就是 \(O(n^3k)\) 的,无法通过,考虑优化。
我们猜测 \(w(l,r)\) 满足四边形不等式,考虑证明,即 \(w(l,r)\) 需满足:
化简可得:
因此原式满足四边形不等式,所以转移具有决策单调性,决策单调性分治即可,复杂度 \(O(n^2k\log n)\)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号