2024.11 - 做题记录与方法总结

风萧萧兮易水寒，壮士一去兮不复还。

2024.11 - 做题记录与方法总结

2024.11.01 ~ 2024.11.12 期中复习&期中考试

2024.11.12

补个题解——[AGC016D] XOR Replace

[AGC016D] XOR Replace

来自 @qzmoot 同一机房的同学题解。

模拟赛用不同的思路场切了。

题面大意：一个序列，一次操作可以将某个位置变成整个序列的异或和。 问最少几步到达目标序列。

来自梦熊的题面：

有一个长度为 \(n\) 的序列 \(a\)，有以下函数:

void update(int u){
	int w=0;
	for(int i=1;i<=n;i++) w^=a[i];
	a[u]=w;
}

你可以执行这个函数若干次，其中参数 \(u\) 由你指定，请问将序列 \(a\) 修改为序列 \(b\) 的最小调用次数是多少。

分析：

操作逻辑简化

我们先要知道这个操作在干什么。

如果你指定一个 \(u\)，使 \(w = a_i\)、\(a_u = \oplus_{i = 1}^n a_i\)，

那么当你再指定一个 \(u^{\prime}\) 时，\(a_{u^{\prime}} = \oplus_{i = 1}^n a_i = w\)。

这是由于异或具有自反性。

那么，这个操作就相当于你有一个初始为 \(a\) 的序列，同时手里还纂着一个 \(\oplus_{i = 1}^n a_i\)，你每次可将手中的数和序列中的数交换，直到序列 \(a\) 变成序列 \(b\)。

合法情况判断

接下来判断的是怎样才是合法的局面。

根据上面的分析，容易发现这个序列 \(a\) 有两种情况：

1. 序列 \(a\) 和序列 \(b\) 的数种类相同，且每种种类的数的个数相同。
2. 序列 \(a\) 和序列 \(b\) 的数种类只有一种不同，该种类数的个数是 \(1\)，且该数为初始的 \(\oplus_{i = 1}^n a_i\)。

最小操作数

接下来是最小操作数的分析。

我们的操作肯定是取出一个数，直接放进与 \(b\) 对应的位置。

因为只有合法局面（序列中的数一定是一一对应的）才会计算最小操作数，所以这样做一定是最优的。

并且 \(a\) 和 \(b\) 已经匹配上的位置可以不用考虑。

那么，你会发现我们的拿取操作形成了一个环或链。

因此，我们可以将 \(a\) 和 \(b\) 中的对应位置的数连边。

其必然形成若干简单环和链，如图：

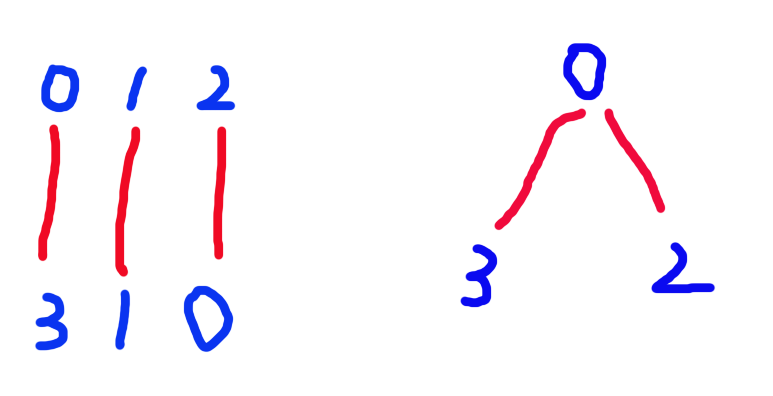
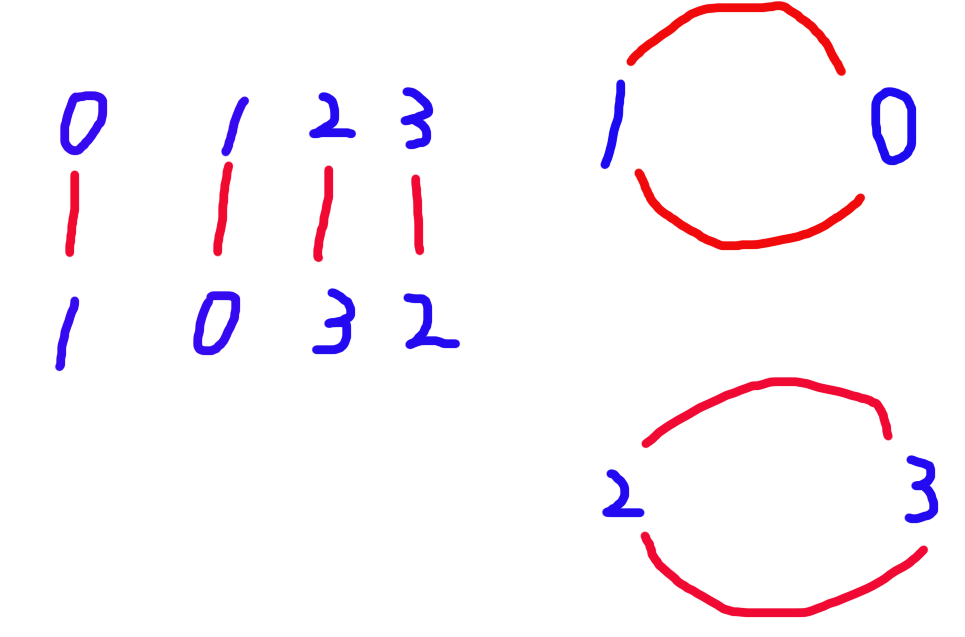
对于链，其中必定有 \(\oplus_{i = 1}^n a_i\)，这时最小操作数为链的边数个数。

对于环，其中必定没有 \(\oplus_{i = 1}^n a_i\)，这时我们会先将 \(\oplus_{i = 1}^n a_i\) 放到任意一个位置，最后将所有环中数字位置调整完后取出来，最小操作数为环的边数 + 1。

用并查集统计答案就可以过了。

最后由于 \(a_i,b_i < 2^{30}\)，所以用并查集计算答案之前需要离散化。

AC-code：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}
void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}
signed main() {
	int n = rd(),top = 0;
	vector<int> a(n),b(n),c(n * 2),s(n * 2),siz(n * 2),t(n * 2);
	vector<bool> bok(n * 2),ext(n * 2);
	vector<int> in(n * 2);
	for(int i = 0;i<n;i++) a[i] = rd();
	for(int i = 0;i<n;i++) b[i] = rd();
	for(int i = 0;i<n;i++) c[top++] = a[i],c[top++] = b[i];
	int w = 0;
	for(int i = 0;i<n;i++) w ^= a[i];
	c.emplace_back(w);	
	sort(c.begin(),c.end());
	top = unique(c.begin(),c.end()) - c.begin() - 1;
	for(int i = 0;i<n;i++) 
		a[i] = lower_bound(c.begin(),c.begin() + top + 1,a[i]) - c.begin(),
		b[i] = lower_bound(c.begin(),c.begin() + top + 1,b[i]) - c.begin();
	w = lower_bound(c.begin(),c.begin() + top + 1,w) - c.begin();
	for(int i = 0;i<n;i++) t[a[i]]++;
	t[w]++;
	for(int i = 0;i<n;i++) {
		t[b[i]]--;
		if(t[b[i]] < 0) {puts("-1");return 0;}
	}
	bool flag = false;
	for(int i = 0;i<n;i++) 
		if(a[i] != b[i]) {flag = true;break;}
	if(!flag) {wt(0);return 0;}
	for(int i = 0;i<n * 2;i++) {s[i] = i;ext[i] = 0;siz[i] = 0;bok[i] = 0;}
	for(int i = 0;i<n;i++) {
		if(a[i] == b[i]) continue;
		bok[a[i]] = bok[b[i]] = true;
		siz[b[i]]++;
		if(w == b[i]) ext[b[i]] = true; 
	}
	auto find = [&](auto self,int x) -> int {
		if(s[x] ^ x) 
			s[x] = self(self,s[x]);
		return s[x];
	};
	for(int i = 0;i<n;i++) {
		if(a[i] == b[i]) continue;
		int fa = find(find,a[i]),fb = find(find,b[i]);
		if(fa != fb) {
			s[fa] = fb;
			siz[fb] += siz[fa];
			ext[fb] = ext[fb] | ext[fa];
		}
	}
	int ans = 0;
	for(int i = 0;i<n * 2;i++) {
		if(bok[i] && find(find,i) == i) {
			if(ext[find(find,i)]) ans += siz[find(find,i)];
			else ans += siz[find(find,i)] + 1;
		}
	}
	wt(ans);
	return 0;
}

2024/11/15

CF1824D LuoTianyi and the Function

题面：

题面翻译

Feyn 给了你一个长度为 \(n\) 的整数数组 \(a\)，下标由 \(1\) 开始。

用以下方式定义函数 \(g(i,j)\)：

• 当 \(i\le j\) 时，\(g(i,j)\) 是满足 $ {a_p:i\le p\le j}\subseteq{a_q:x\le q\le j} $ 的最大整数 \(x\)；
• 否则 \(g(i,j)=0\)。

\(q\) 次询问，每次给定 \(l,r,x,y\)，请求出 \(\sum\limits_{i=l}^r\sum\limits_{j=x}^y g(i,j)\) 的值。

数据范围：\(1\leq n,q \leq 10^6\)，\(1\leq l \leq r \leq n\)，\(1\leq x \leq y \leq n\)，\(1\leq a_i \leq n\)

(translated by 342873)

样例 #1

样例输入 #1

6 4
1 2 2 1 3 4
1 1 4 5
2 3 3 3
3 6 1 2
6 6 6 6

样例输出 #1

6
6
0
6

样例 #2

样例输入 #2

10 5
10 2 8 10 9 8 2 1 1 8
1 1 10 10
2 2 3 3
6 6 6 6
1 1 4 5
4 8 4 8

样例输出 #2

4
2
6
4
80

拆式子

式子都给我们了，上手考虑拆贡献。

因为 \(g(i,j)\) 是独立的，有：

\[\sum\limits_{i=l}^r\sum\limits_{j=x}^y g(i,j) = \sum\limits_{i=l}^r\sum\limits_{j=1}^y g(i,j) - \sum\limits_{i=l}^r\sum\limits_{j=1}^{x-1} g(i,j) \]

题目中说：当 \(i > j\) 时，\(g(i,j) = 0\)

所以有：

\[\begin{aligned} \sum\limits_{i=l}^r\sum\limits_{j=x}^y g(i,j) &= \sum\limits_{i=l}^r\sum\limits_{j=1}^y g(i,j) - \sum\limits_{i=l}^r\sum\limits_{j=1}^{x-1} g(i,j) \\ &= \sum\limits_{i=l}^{\min(r,y)}\sum\limits_{j=1}^y g(i,j) - \sum\limits_{i=l}^{\min(r,x - 1)}\sum\limits_{j=1}^{x-1} g(i,j)\\ &= \sum\limits_{j=1}^y\sum\limits_{i=l}^{\min(r,y)} g(i,j) - \sum\limits_{j=1}^{x-1}\sum\limits_{i=l}^{\min(r,x - 1)} g(i,j) \end{aligned} \]

对于外面这一维求和（即 \(\sum\limits_{j = 1}\)），我们可以扫描线去做。

里面这一维求和（即 \(\sum\limits_{i = l}^{r^{\prime}}\)），我们可以做一个历史和，也就是计算当 \(j:1\sim k\) 时，\(g(i,j)\) 对于 \(i:l\sim r^{\prime}\) 产生的 \(k\) 个版本的贡献的总和。

我们可以把询问离线下来，将询问拆开，分别插入到区间的右端点上，在遍历的时候计算答案。

因为我们做的是前缀和差分，插入的时候记得记录贡献的符号！

贡献的计算

为了直观的体会贡献是如何变化的，可以手模一些例子：

如图：

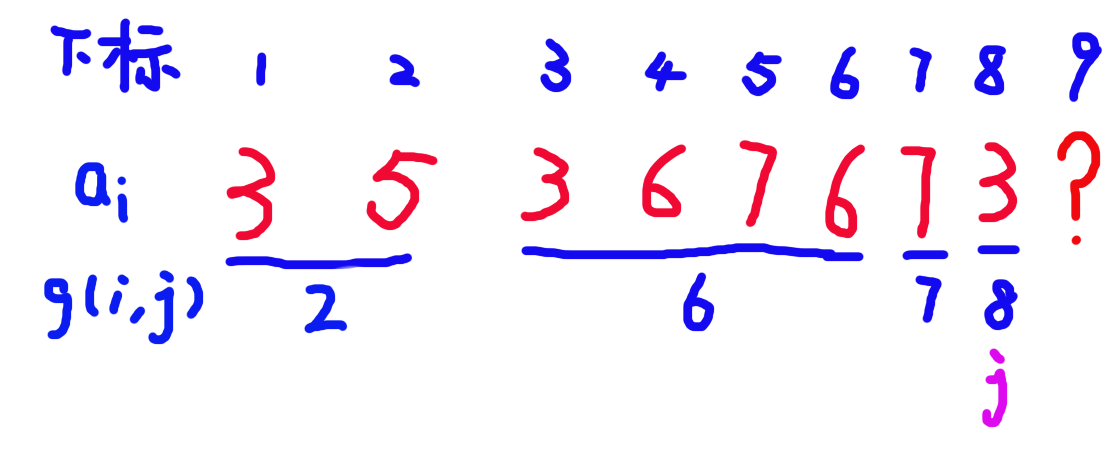
这是当 \(j = 8\) 时的 \(g(i,j)\) 数组。

考虑 \(j = 9\) 时的情况：

1. 当 \(a_9 = 6\) 时，如图：
   
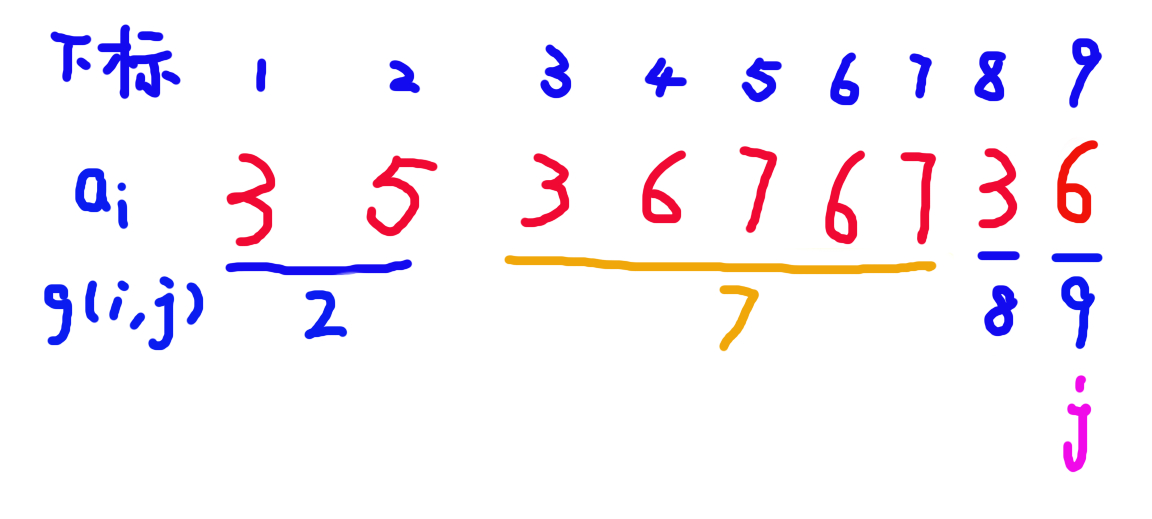
   此时上一个 \(6\) 所在的颜色段和其下一个颜色段合并了，并且贡献变为其下一个颜色段的 \(g(i,j)\)，在末尾新增了一个 \(g(i,j) = 9\) 的新颜色段。

2. 当 \(a_9 = 4\) 时，如图：
   
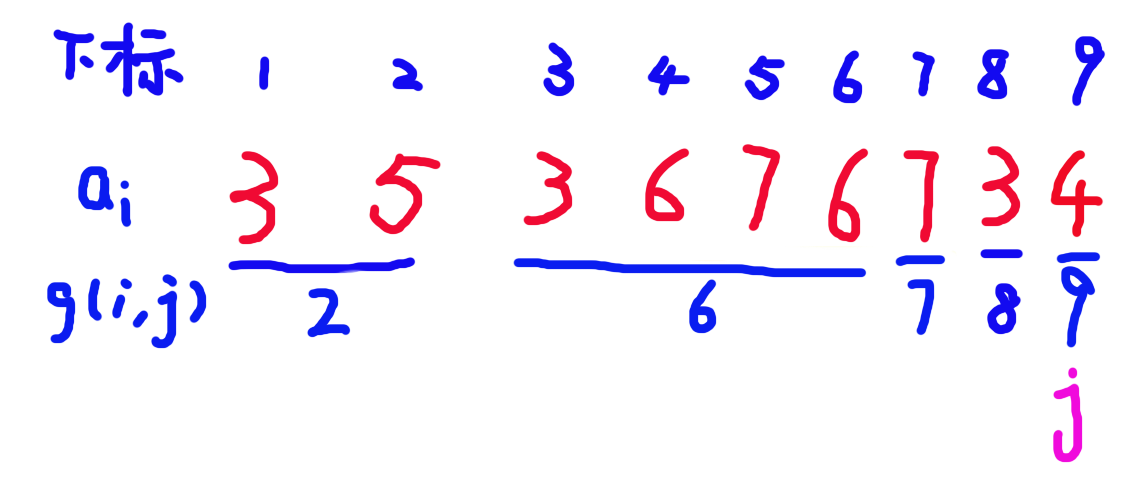
   由于先前没有 \(a_i = 4\)，所以只在末尾新增了一个 \(g(i,j) = 4\) 的新颜色段。

所以，我们可以用set维护这些颜色段，在扫描的时候判断是否需要合并两个颜色段，并不断在末尾新增颜色段。

当两个颜色段合并时，用历史和线段树做区间覆盖操作。

在所有操作结束之后，更新历史和。

最后将答案输出即可。

常数问题

我喜欢通过构造矩阵来计算历史和。

但这道题卡常。

显然，类似于 [NOIP2022] 比赛，我们需要将矩阵拆开。

我们一共有两种矩阵：

1. 覆盖矩阵

\[\begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & d \\ 0 & 0 & 1 \\ \end{bmatrix} \]

2. 更新矩阵

\[\begin{bmatrix} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \]

可以发现我们实际需要维护的位置只有 \((a,b,c,d)\)：

\[\begin{bmatrix} 1 & a & b \\ 0 & c & d \\ 0 & 0 & 1 \\ \end{bmatrix} \]

那么手模矩阵乘法就可以将 \(3^3\) 的常数减小到 \(3\sim 4\) 左右。

AC-code：

我的代码常数比较大，所以用快读 和 C++20 64bits winlibs 选项才能过。

#include<bits/stdc++.h>
using namespace std;
#define int long long
namespace IO {
	inline char gc() {
		static const int IN_LEN = 1 << 18 | 1;
		static char buf[IN_LEN], *s, *t;
		return (s == t) && (t = (s = buf) + fread(buf, 1, IN_LEN, stdin)), s == t ? -1 : *s++;
	}
	template <typename T>
	inline void read(T &x) {
		static char ch, ff;
		ch = gc(), ff = 0;
		for(; !isdigit(ch); ch = gc())
			ff |= ch == '-';
		for(x = 0; isdigit(ch); ch = gc())
			x = (x << 3) + (x << 1) + (ch ^ 48);
		ff && (x = -x);
		return;
	}
	template <typename T, typename ...t>
	void read(T&x, t& ...y) {
		read(x), read(y...);
		return;
	}
	template <typename T>
	inline void print(T x) {
		static int pr, pri[105], temp;
		pr = 0, temp = x;
		if(x < 0)
			fputc('-', stdout), x = -x;
		if(!x) {
			fputc(48, stdout);
			return;
		}
		while(x)
			pri[++pr] = x % 10, x /= 10;
		for(; pr; pr--)
			fputc(pri[pr] + 48, stdout);
		x = temp;
		return;
	}
	template <typename T, typename ...t>
	void print(T&x, t& ...y) {
		print(x), fputc(' ', stdout), print(y...);
		return;
	}
}
using namespace IO;


struct tag{
    int x[7];
    inline void init() {
        x[1] = x[4] = x[6] = 1;
        x[2] = x[3] = x[5] = 0;
    }
    inline int& operator [](const int pos) {return x[pos];}
	inline friend tag operator * (tag& A,tag& B) {
        tag c;c.init();
        c[2] = A[2] * B[4] + B[2];
        c[3] = B[3] + A[2] * B[5] + A[3];
		c[4] = A[4] * B[4];
        c[5] = B[5] * A[4] + A[5];
        return c;
    }
    inline friend bool operator != (tag A,tag B) {
        for(int i = 0;i<7;i++)
            if(A[i] != B[i])
                return true;
        return false;
    }
    inline void print(string s) {
        cout<<"test for "<<s<<" matrix\n";
        cout<<x[1]<<' '<<x[2]<<' '<<x[3]<<'\n';
        cout<<0<<' '<<x[4]<<' '<<x[5]<<'\n';
        cout<<0<<' '<<0<<' '<<x[6]<<'\n'; 
   }
};

inline tag addtag(int k) {tag c;c.init();c[4] = 0;c[5] = k;return c;}
inline tag updtag() {tag c;c.init();c[2] = 1;return c;}
inline tag NONE(){tag c;c.init();return c;}

struct vet{
    int y[4];
    void init() {y[1] = y[2] = y[3] = 0;}
    int& operator [](const int pos) {return y[pos];}
    inline friend vet operator + (vet a,vet b) {
        vet c;c.init();
        c[1] = a[1] + b[1];
        c[2] = a[2] + b[2];
        c[3] = a[3] + b[3];
        return c;
    }
    inline void print(string s) {
        cout<<'\n';
        cout<<"test for "<<s<<" vector\n";
        cout<<y[1]<<'\n';
        cout<<y[2]<<'\n';
        cout<<y[3]<<'\n';
        cout<<'\n';
    }
};

inline vet operator * (tag A,vet B) {
    vet c;c.init();
    c[1] = B[1] + B[2] * A[2] +B[3] * A[3];
    c[2] = B[2] * A[4] + A[5] * B[3];
    c[3] = B[3];
    return c;
}

const int N = 1e6+5;
int n,q,a[N],ans[N],pre[N];
vector<array<int,4>> R[N];
set<int> s;

#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)
tag T[N<<2];vet V[N<<2];
bool ext[N<<2];

inline void push_up(int p) {
	V[p] = V[ls] + V[rs];
}

inline void addtag(int p,tag x){
	V[p] = x * V[p];
	T[p] = x * T[p];
	ext[p] = true;
}

inline void push_down(int p){
	if(ext[p]) {
		addtag(ls,T[p]);
		addtag(rs,T[p]);
		T[p].init();
		ext[p] = false;
	}
}

inline void build(int p,int pl,int pr) {
	T[p].init();
	V[p].init();
	if(pl == pr) {
		V[p][3] = 1;
		return;
	}
	build(ls,pl,mid);
	build(rs,mid+1,pr);
	push_up(p);
}

inline void update(int p,int pl,int pr,int l,int r,tag x) {
	if(l <= pl && pr <= r) {addtag(p,x);return;}
	push_down(p);
	if(l <= mid) update(ls,pl,mid,l,r,x);
	if(r > mid) update(rs,mid+1,pr,l,r,x);
	push_up(p);
}

inline vet query(int p,int pl,int pr,int l,int r){
	if(l <= pl && pr <= r) return V[p];
	push_down(p);
	if(r <= mid) return query(ls,pl,mid,l,r);
	else if(l > mid) return query(rs,mid+1,pr,l,r);
	else return query(ls,pl,mid,l,r) + query(rs,mid+1,pr,l,r);
}

signed main() {
	read(n,q);
	for(int i = 1;i<=n;i++) read(a[i]);
	for(int i = 1,l,r,x,y;i<=q;i++) {
		read(l,r,x,y);
		R[x - 1].emplace_back((array<int,4>){-1,l,min(r,x - 1),i});
		R[y].emplace_back((array<int,4>){1,l,min(r,y),i});
	}
	s.insert(0);
	build(1,1,n);
	for(int i = 1;i<=n;i++) {
		auto it = s.lower_bound(pre[a[i]]);
		if(it != s.begin()) {
			int l = *(--it),v;
			++it;++it;
			v = (it == s.end()) ? i : (*it);
			if(l < pre[a[i]]) update(1,1,n,l+1,pre[a[i]],addtag(v));
		}
		update(1,1,n,i,i,addtag(i));
		if(pre[a[i]]) s.erase(pre[a[i]]);
		s.insert(i);
		pre[a[i]] = i;
		update(1,1,n,1,i,updtag());
		for(auto c:R[i]) 
			if(c[1] <= c[2]) 
				ans[c[3]] += c[0] * query(1,1,n,c[1],c[2])[1];
	}
	for(int i = 1;i<=q;i++) print(ans[i]), fputc('\n', stdout);
	return 0;
}

CF1476F Lanterns

待补；

2024/11/26

把之前模拟赛考过的题，搬一搬。

Day1 俗

给定一个长度为 \(n\) 的序列 \(a_i\) ,有一个长度为 \(m\) 的序列 \(b_i\) ，序列 \(b\) 的初始值均为 \(0\) 。接下来进行 \(q\) 次操作。

1. 给定 \(l,r,x\) ，将所有 \(l \leq i \leq r\) 的 \(a_i\) 的值修改成 \(x\) ；
2. 给定 \(l,r,x\) ，对于每一个 \(l \leq i \leq r\) ，如果 \(a_i \not = 0\) ，则将 \(b_{a_i}\) 加上 \(x\) 。

查询经过这 \(q\) 次操作之后得到的序列 \(b\) 。

时间限制 1.5 秒，空间限制 512 MB 。

输入的第一行包含三个正整数 \(n,m,q\) 。

输入的第二行包含 \(n\) 个非负整数 \(a_i\) 。

接下来 \(q\) 行，每行给出四个正整数 \(opt,l,r,x\) ，当 \(opt=1\) 表示上述第一种操作，当 \(opt=2\) 表示上述第二种操作。

输出的第一行包含 \(m\) 个非负整数，第 \(i\) 个数表示经过所有操作后的最终的序列 \(b\) 的第 \(i\) 个元素的值。

input:

3 3 3
1 2 3
2 2 3 1
1 3 3 2
2 1 3 2

output:

2 5 1

上来就发现，我们的修改太散了。每次询问区间颜色，对于区间的颜色 \(+x\)，最后问每种颜色的累加值。

还要支持区间修改颜色！

这个时候，得请出珂朵莉树（ODT）！

我们发现这个操作是区间推平（assign），区间询问。

妥妥的珂朵莉树。

当询问的时候，对于整个颜色段进行询问，就可以快速计算答案。

但是如果只有查询，每个点颜色还不同，珂朵莉树就暴毙了。

我们考虑只有询问的时候，直接做差分前缀和，最后统一计算答案。

#include<bits/stdc++.h>
using namespace std;
#define int long long
namespace FastIO {
	char buf[1 << 10], buf2[1 << 21], a[21], *p1 = buf, *p2 = buf, hh = ' ';
	int p, p3 = -1;
	void read() {}
	void print() {}
	inline int getc() {
		return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 10, stdin), p1 == p2) ? EOF : *p1++;
		//   缓冲区以空    p2赋成读入后的地址，p1赋成头地址，尝试读入      是否相等  结束读入 返回p1,p1向后挪
	}
	inline void flush() {
		fwrite(buf2, 1, p3 + 1, stdout), p3 = -1;
	}
	inline void read(int &x) {
		x = 0;
		char ch = getc();
		while (!isdigit(ch)) {
			ch = getc();
		}
		while (isdigit(ch)) {
			x = (x << 1) + (x << 3) + (ch ^ '0');
			ch = getc();
		}
	}
	inline void print(int x) {
		if (p3 > 1 << 21) flush();
		if (x < 0) buf2[++p3] = '-', x = -x;
		do {
			a[++p] = x % 10 + 48;
		} while (x /= 10);
		do {
			buf2[++p3] = a[p];
		} while (--p);
		buf2[++p3] = hh;
	}
}
#define read FastIO::read
#define print FastIO::print
const int N = 5e5+5,M = 1e6 + 5;
int n,m,q,a[N],b[M];
struct node{
	int l,r,v;
	friend bool operator < (const node a,const node b) {
		return a.l < b.l;
	}
	node (int l,int r = 0,int v = 0) : l(l),r(r),v(v) {}
};

set<node> s;
#define iter set<node>::iterator

iter split(int x) {
	iter it = s.lower_bound(node(x));
	if(it != s.end() && it->l == x) return it;
	it--;
	if(it->r < x) return s.end();
	int l = it->l,r = it->r,v = it->v;
	s.erase(it);s.insert(node(l,x-1,v));
	return s.insert(node(x,r,v)).first;
}

void assign(int l,int r,int x) {
	iter rt = split(r + 1),lf = split(l);
	s.erase(lf,rt);s.insert(node(l,r,x));
}

void add(int l,int r,int x) {
	iter rt = split(r + 1),lf = split(l);
	for(iter it = lf;it != rt;it++) 
		b[it->v] += (it->r - it->l + 1) * x;
}

int c[N];
array<int,4> Q[N];

signed main() {
    freopen("b.in","r",stdin);
    freopen("b.out","w",stdout);
    read(n);read(m);read(q);
	for(int i = 1;i<=n;i++) {
		read(a[i]);
		s.insert(node(i,i,a[i]));
	}
	bool fg = true;
	for(int i = 1;i<=q;i++) {
		int op,l,r,x;
		read(op),read(l),read(r),read(x);
		Q[i] = {op,l,r,x};
		if(op == 1) fg = false;
	}
	if(fg) {
		for(int i = 1;i<=q;i++) {
			int l = Q[i][1],r = Q[i][2],w = Q[i][3];
			c[l] += w,c[r + 1] -= w;
		}
		for(int i = 1;i<=n;i++) c[i] = c[i - 1] + c[i];
		for(int i = 1;i<=m;i++) b[a[i]] += c[i];
		for(int i = 1;i<=m;i++) print(b[i]);
		FastIO :: flush();
		return 0;
	}
	for(int i = 1;i<=q;i++){
		int op,l,r,x;
		op = Q[i][0],l = Q[i][1],r = Q[i][2],x = Q[i][3];
		if(op == 1) assign(l,r,x);
		else add(l,r,x);
	}
	for(int i = 1;i<=m;i++) print(b[i]);
	FastIO :: flush();
	
	return 0;
}

CF896C Willem, Chtholly and Seniorious

ODT诞生的题。

题面：

题面翻译

【题面】
请你写一种奇怪的数据结构，支持：

• \(1\) \(l\) \(r\) \(x\) ：将\([l,r]\) 区间所有数加上\(x\)
• \(2\) \(l\) \(r\) \(x\) ：将\([l,r]\) 区间所有数改成\(x\)
• \(3\) \(l\) \(r\) \(x\) ：输出将\([l,r]\) 区间从小到大排序后的第\(x\) 个数是的多少(即区间第\(x\) 小，数字大小相同算多次，保证 \(1\leq\) \(x\) \(\leq\) \(r-l+1\) )
• \(4\) \(l\) \(r\) \(x\) \(y\) ：输出\([l,r]\) 区间每个数字的\(x\) 次方的和模\(y\) 的值(即(\(\sum^r_{i=l}a_i^x\) ) \(\mod y\) )

【输入格式】
这道题目的输入格式比较特殊，需要选手通过\(seed\) 自己生成输入数据。
输入一行四个整数\(n,m,seed,v_{max}\) （$1\leq $ \(n,m\leq 10^{5}\) ,\(0\leq seed \leq 10^{9}+7\) $,1\leq vmax \leq 10^{9} $ ）
其中\(n\) 表示数列长度，\(m\) 表示操作次数，后面两个用于生成输入数据。
数据生成的伪代码如下

其中上面的op指题面中提到的四个操作。

【输出格式】
对于每个操作3和4，输出一行仅一个数。

样例 #1

样例输入 #1

10 10 7 9

样例输出 #1

2
1
0
3

样例 #2

样例输入 #2

10 10 9 9

样例输出 #2

1
1
3
3

提示

In the first example, the initial array is $ {8,9,7,2,3,1,5,6,4,8} $ .

The operations are:

• $ 2\ 6\ 7\ 9 $
• $ 1\ 3\ 10\ 8 $
• $ 4\ 4\ 6\ 2\ 4 $
• $ 1\ 4\ 5\ 8 $
• $ 2\ 1\ 7\ 1 $
• $ 4\ 7\ 9\ 4\ 4 $
• $ 1\ 2\ 7\ 9 $
• $ 4\ 5\ 8\ 1\ 1 $
• $ 2\ 5\ 7\ 5 $
• $ 4\ 3\ 10\ 8\ 5 $

直接上珂朵莉树，暴力累加，暴力修改，对颜色段暴力排序，暴力计算。

#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}
void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

struct node{
	int l,r;
	mutable int v;
	node(int l,int r = 0,int v = 0) : l(l),r(r),v(v){};
	friend bool operator < (const node a,const node b) {return a.l < b.l;}
};
const int N = 1e5+5,Mod = 1e9 + 7;
int n,m,seed,vm,a[N];
set<node> s;
int rnr(){
	int ret = seed;
	seed = (seed * 7 + 13) % Mod;
	return ret;
}

#define iter set<node>::iterator 

iter spilt(int x){
	iter it = s.lower_bound(node(x));
	if(it != s.end() && it->l == x) return it;
	it--;
	if(it->r < x) return s.end();
	int l = it->l,r = it->r,v = it->v;
	s.erase(it);s.insert(node(l,x - 1,v));
	return s.insert(node(x,r,v)).first;
}

void add(int l,int r,int x) {
	iter rt = spilt(r + 1),lf = spilt(l);
	for(iter it = lf;it != rt;it++) it->v += x;
}
#define ll long long
#define split spilt
#define Node node


void assign(int l,int r,int x){
	iter rt = spilt(r + 1),lf = spilt(l);
	s.erase(lf,rt);
	s.insert(node(l,r,x));
} 

struct Rank{
	int num,cnt;
	Rank(int n,int c) : num(n),cnt(c){}
	friend bool operator < (const Rank a,const Rank b) {
		return a.num < b.num;
	}
};

int getkth(int l,int r,int x) {
	iter rt = spilt(r + 1),lf = spilt(l);
	vector<Rank> P;
	for(iter it = lf;it != rt;it++) P.push_back(Rank(it->v,it->r - it->l + 1));
	sort(P.begin(),P.end());int i;
	for(i = 0;i<P.size();i++) {
		if(P[i].cnt < x) x -= P[i].cnt;
		else break;
	}	
	return P[i].num;
}

int qpow(int x,int k,int mod) {
	int re = 1;
	x %= mod;
	while(k) {
		if(k & 1) re = (re * x) % mod;
		x = (x * x) % mod;
		k >>= 1;
	}
	return re;
}

int geT(int l,int r,int k,int mod) {
	iter rt = spilt(r + 1),lf = spilt(l);
	int ans = 0;
	for(iter it = lf;it != rt;it++) ans = (ans + qpow(it->v,k,mod) * (it->r - it->l + 1) % mod) % mod;
	return ans;
}

signed main() {
	n = rd(),m = rd(),seed = rd(),vm = rd();
	for(int i = 1;i<=n;i++) {
		a[i] = (rnr() % vm) + 1;
		s.insert(node(i,i,a[i]));
	}
	while(m--) {
		int op = (rnr() % 4) + 1;
		int l = (rnr() % n) + 1;
		int r = (rnr() % n) + 1;
		if(l > r) swap(l,r);
		int x = 0,y = 0;
		switch(op) {
			case 1:
				x = (rnr() % vm) + 1;
				add(l,r,x);
				break;
			case 2:
				x = (rnr() % vm) + 1;
				assign(l,r,x);
				break;
			case 3:
				x = (rnr() % (r - l + 1)) + 1;
				wt(getkth(l,r,x));putchar('\n');
				break;
			case 4:
				x = (rnr() % vm) + 1;
				y = (rnr() % vm) + 1;
				wt(geT(l,r,x,y));putchar('\n');
				break;
			default:
				puts("Error");
				exit(0);
				break;
		}
	}
	
	return 0;
}

Day1夜间场 独

给定一棵 \(n\) 个节点的树，以点 \(1\) 为根节点，初始所有节点的颜色均为 \(1\) 。接下来进行两种类型的操作：

1. 给定点 \(x\) 和颜色 \(y\) ，将以点 \(x\) 为根的子树的全部节点的颜色染成颜色 \(y\) 。
2. 给定节点 \(x\) ，询问如果将所有两端点对应颜色不同的边全部删掉，那么点 \(x\) 所在连通块的大小。

时间限制 2 秒，空间限制 1024 MB。

由于评测机效率差异原因，本题时间限制修改为 4 秒。

输入的第一行包含一个正整数 \(n\) ，表示树的节点数量。

输入的第 \(2\) 行到第 \(n\) 行每行输入两个正整数 \(u,v\) 表示树上的一条边 \((u,v)\) 。

输入的第 \(n+1\) 行包含一个正整数 \(m\) ，表示操作的数量。

接下来 \(m\) 行，每行首先输入一个正整数 \(opt\) 表示操作类型。当 \(opt=1\) 时输入 \(x,y\) ；当 \(opt=2\) 时输入 \(x\) 。

对于每组询问，输出对应的结果。

input:

6
1 2
2 3
2 4
1 5
3 6
8
2 1
1 1 2 
2 1
1 2 3
2 1
1 1 3
2 1
2 3

output:

6
6
2
6
6

先上树剖，没有异议吧。

首先，我们直接去找显然很麻烦。

我们不仅得考虑子树内的，还有子树外的。

干脆我们想办法只考虑子树内的！

我们尝试快速找到同一颜色深度最小的点。

考虑用 set 维护。

因为我们已经用了set，想到珂朵莉是很正常的吧！

我们用set维护树上颜色段！

我们设 \(val_i\) 为与 \(i\) 同色的连通块大小，\(col_i\) 为 \(i\) 及其颜色段颜色，\(F_i\) 为 \(i\) 在它之上的颜色段顶（\(i\) 为连通块顶）。

如果染色点是 root，那么我们清空set，换成巨大颜色段，\(col_i = x,val_i = n\)。

否则，我们将 \(i\) 子树内颜色段的 \(val_i,F_i\) 转移，子树在set的颜色段标记清空，

用树剖线段树维护所在的连通块顶即可，在推平子树的时候做颜色覆盖操作。

AC-code:

#include<bits/stdc++.h>
using namespace std;
int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}

void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}
const int N = 1e6+5;
set<int> s;
int n,m,head[N],nxt[N<<1],to[N<<1],cnt;
void init(){memset(head,-1,sizeof(head));cnt = 0;}
void add(int u,int v) {
	nxt[cnt] = head[u];
	to[cnt] = v;
	head[u] = cnt++;
}
int id[N],siz[N],fa[N],num,_id[N];
void dfs1(int x,int f) {
	fa[x] = f;
	siz[x] = 1;
	id[x] = ++num;
	_id[num] = x;
	for(int i = head[x];~i;i = nxt[i]) {
		int y = to[i];
		if(y ^ f) {
			dfs1(y,x);
			siz[x] += siz[y];
		}
	}
}
namespace sgt{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)
int tag[N << 2];

inline void addtag(int p,int d) {
	tag[p] = d;
}

inline void push_down(int p) {
	if(tag[p]) {
		addtag(ls,tag[p]);
		addtag(rs,tag[p]);
		tag[p] = 0;
	}
} 

void assign(int p,int pl,int pr,int l,int r,int d) {
	if(l <= pl && pr <= r) {addtag(p,d);return;}
	push_down(p);
	if(l <= mid) assign(ls,pl,mid,l,r,d);
	if(r > mid) assign(rs,mid+1,pr,l,r,d);
}

int query(int p,int pl,int pr,int x) {
	if(pl == pr) return tag[p];
	push_down(p);
	if(x <= mid) return query(ls,pl,mid,x);
	else return query(rs,mid+1,pr,x);
}

}

bool insubtree(int x,int y) {
	if(!y) return false;
	return id[y] <= id[x] && id[x] <= id[y] + siz[y] - 1;
}

int val[N],col[N],F[N];

signed main() {
    freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);
	init();
	n = rd();
	for(int i = 1;i<n;i++) {
		int u = rd(),v = rd();
		add(u,v);add(v,u);
	}
	dfs1(1,0);
	sgt::assign(1,1,n,1,n,1);
	val[1] = n;col[1] = 1;s.insert(1);
	m = rd();
	while(m--) {
		int op = rd();
		if(op == 1) {
			int x = rd(),y = rd();
			if(x == 1) {
				for(auto it : s) val[_id[it]] = col[_id[it]] = F[_id[it]] = 0;
				s.clear();s.insert(1);
				val[1] = n;col[1] = y;
				sgt::assign(1,1,n,1,n,1);
				continue;
			}
			int lst = 0;
			for(auto it = s.lower_bound(id[x]);it != s.end() && (*it) <= id[x] + siz[x] - 1;it = s.lower_bound(id[x])) {
				int w = _id[*it];
				if(insubtree(w,lst)) {
					s.erase(id[w]);val[w] = col[w] = F[w] = 0;
					continue;
				}
				lst = w;
				int z = F[w];
				val[z] += siz[w];
				s.erase(id[w]),val[w] = col[w] = F[w] = 0;
			}
			int NFA = sgt::query(1,1,n,id[fa[x]]);
			if(col[NFA] == y) {
				sgt::assign(1,1,n,id[x],id[x] + siz[x] - 1,NFA);
				continue;
			}
			s.insert(id[x]);sgt::assign(1,1,n,id[x],id[x] + siz[x] - 1,x);
			F[x] = NFA;val[x] = siz[x];val[NFA] -= siz[x],col[x] = y;
		}else {
			int x = rd();
			if(col[x]) wt(val[x]),putchar('\n');
			else {
				int NFA = sgt::query(1,1,n,id[fa[x]]);
				wt(val[NFA]),putchar('\n');
			}
		}
	}
	
	return 0;
}

Day3 高

给定一棵 \(n\) 个节点的树，第 \(i\) 个节点的颜色为 \(a_i\) 。

接下来我们可以割掉这棵树上的若干条边，使得这棵树被分割成若干个连通块，我们定义一种割边方案的权值为，对于一个连通块，若存在一种颜色的所有点均在该连通块内，则该连通块权值为 >\(1\) ，否则为 \(0\) ，一种割边方案的权值即为其分割出来的所有连通块的权值和。

询问最大的可行的割边方案的权值。

时间限制 6 秒，空间限制 1024 MB。

输入的第一行包含一个正整数 \(t\) ，表示测试数据组数。对于每组测试数据：

输入的第一行包含一个正整数 \(n\) ，表示树的大小。

输入的第二行包含 \(n\) 个正整数 \(a_1 , \dots , a_n\) 。

接下来输入 \(n-1\) 行，每行两个正整数 \(u,v\) 描述树上一条边 \((u,v)\) 。

对于每组测试数据，输出一行一个整数表示最大的可行的割边方案的权值。

input:

3
6
3 1 2 2 1 2 
1 2
1 3
3 4
3 5
3 6
4
3 3 2 2 
1 2
2 3
2 4
6
1 3 1 2 1 3 
1 2
2 3
1 4
1 5
3 6

output:

2
1
2

很好很好的树上贪心题。

我们发现贡献很特别！只有 \(0,1\) 两种，那么我们肯定是贡献的块越小越好。

因为如果贡献的块很大，而有方案可以让他更小，前者贡献肯定是 \(1\)，后者贡献是 \(1\uparrow\)。

那么我们在对树dfs时，直接判断是否 \(col\) 已经合法，然后对子树进行一次用过的col标记，并将答案 \(+1\)。

然后对对子树打上 \(vis\) 标记，下一次产生贡献时不经过该子树。

这样复杂度就是 \(\mathcal{O}(n)\) 的。

但是这道题卡常！

考虑树剖求 \(lca\)！

但是还不够！！

拆头文件！！！

但是还不够！！！！

究极大杀器————bitset

我们发现有 \(vis、col\) 0/1 标记，我们用bitset维护能减少很多常数。

AC-code：

#include<algorithm>
#include<cstdio>
#include<ctype.h>
#include<bitset>
using namespace std;
namespace FastIO {
	char buf[1 << 10], buf2[1 << 21], a[21], *p1 = buf, *p2 = buf, hh = '\n';
	int p, p3 = -1;
	void read() {}
	void print() {}
	inline int getc() {
		return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 10, stdin), p1 == p2) ? EOF : *p1++;
		//   缓冲区以空    p2赋成读入后的地址，p1赋成头地址，尝试读入      是否相等  结束读入 返回p1,p1向后挪
	}
	inline void flush() {
		fwrite(buf2, 1, p3 + 1, stdout), p3 = -1;
	}
	inline void read(int &x) {
		x = 0;
		char ch = getc();
		while (!isdigit(ch)) {
			ch = getc();
		}
		while (isdigit(ch)) {
			x = (x << 1) + (x << 3) + (ch ^ '0');
			ch = getc();
		}
	}
	inline void print(int x) {
		if (p3 > 1 << 21) flush();
		if (x < 0) buf2[++p3] = '-', x = -x;
		do {
			a[++p] = x % 10 + 48;
		} while (x /= 10);
		do {
			buf2[++p3] = a[p];
		} while (--p);
		buf2[++p3] = hh;
	}
}
#define read FastIO::read
#define print FastIO::print
__attribute__((optimize("Ofast")))
const int N = 1e6+5;
int n,a[N],head[N],nxt[N<<1],to[N<<1],cnt,top[N],siz[N],son[N],dep[N],fa[N];
inline void init(){for(register int i = 1;i<=n;i++) head[i] = -1,son[i] = 0;cnt = 0;}
inline void add(int u,int v) {
	nxt[cnt] = head[u];
	to[cnt] = v;
	head[u] = cnt++;
}
void dfs1(int x,int f) {
	fa[x] = f;
	siz[x] = 1;
	dep[x] = dep[f] + 1;
	for(register int i = head[x];~i;i = nxt[i]) {
		int y = to[i];
		if(y ^ f) {
			dfs1(y,x);
			siz[x] += siz[y];
			if(siz[son[x]] < siz[y]) son[x] = y;
		}
	}
}
void dfs2(int x,int topx) {
	top[x] = topx;
	if(!son[x]) return;
	dfs2(son[x],topx);
	for(register int i = head[x];~i;i = nxt[i]) {
		int y = to[i];
		if(y ^ fa[x] && y ^ son[x]) dfs2(y,y);
	}
}

inline int LCA(int x,int y) {
	while(top[x] ^ top[y]) {
		if(dep[top[x]] < dep[top[y]]) swap(x,y);
		x = fa[top[x]];
	}
	return dep[x] < dep[y] ? x : y;
}
struct link{
	int head[N],nxt[N],to[N],cnt;
	inline void init(){for(register int i = 1;i<=n;i++) head[i] = -1;cnt = 0;}
	inline void add(int x,int w) {
		nxt[cnt] = head[x];
		to[cnt] = w;
		head[x] = cnt++;
	}
}q,k;
int ans = 0;
bitset<N> col,vis;

void down(int x) {
	col[a[x]] = true;
	vis[x] = true;
	for(register int i = head[x];~i;i = nxt[i]) {
		int y = to[i];
		if(y ^ fa[x] && !vis[y]) 
			down(y);
	}
}

void solve(int x) {
	for(register int i = head[x];~i;i = nxt[i]) {
		int y = to[i];
		if(y ^ fa[x]) 
			solve(y);
	}
	for(register int i = q.head[x];~i;i = q.nxt[i]) {
		int y = q.to[i];
		if(col[y]) continue;
		down(x);
		ans++;
	}
}

int st[N],tot;
inline void solve() {
	read(n);init();ans = 0;tot = 0;
	k.init(),q.init();
	for(register int i = 1;i<=n;i++) read(a[i]);
	for(register int i = 1;i<=n;i++) st[++tot] = a[i];
	for(register int i = 1;i<n;i++) {
		int u,v;read(u);read(v);
		add(u,v);add(v,u);
	}
	sort(st + 1,st + tot + 1);
	tot = unique(st + 1,st + tot + 1) - st - 1;
	for(register int i = 1;i<=n;i++) a[i] = lower_bound(st + 1,st + tot + 1,a[i]) - st;
	for(register int i = 1;i<=n;i++) k.add(a[i],i);
	dfs1(1,0);dfs2(1,1);
	for(register int i = 1;i<=tot;i++) {
		int cnt = 1,L = 1;
		for(register int j = k.head[i];~j;j = k.nxt[j])
			if(cnt) L = k.to[j],cnt = 0;
			else L = LCA(k.to[j],L);
		q.add(L,i);
	}
	solve(1);
	print(ans);
	FastIO :: flush();
	for(register int i = 1;i<=n;i++) col[i] = vis[i] = false;
}

signed main() {
	int t;read(t);
	while(t--) solve();
	return 0;
}

Day3夜间场 将不可解的我的一切

给定一个正整数 \(n\)，找出每一个 \(k\) 进制下的没有前导零的正整数 \(x\) 使得 \(x\) 的每一位的和等于 \(n\)，记所有这样的 \(x\) 组成一个集合 \(S\)。

对于 \(S\) 中的每一个数 \(x\)，求出它每一位的乘积为 \(f(x)\)，令所有的 \(f(x)\) 组成一个集合 \(T\)。求集合 \(T\) 的大小，答案对 \(10^9+7\) 取模。

给定一个正整数 \(n\)，找出每一个 \(k\) 进制下的没有前导零的正整数 \(x\) 使得 \(x\) 的每一位的和等于 \(n\)，记所有这样的 \(x\) 组成一个集合 \(S\)。

对于 \(S\) 中的每一个数 \(x\)，求出它每一位的乘积为 \(f(x)\)，令所有的 \(f(x)\) 组成一个集合 \(T\)。求集合 \(T\) 的大小，答案对 \(10^9+7\) 取模。

本题包含多组测试数据。第一行一个正整数 \(t\) 表示测试数据的数量。

接下来 \(t\) 行，每行两个正整数 \(n, k\)。

对于每组数据，输出一行一个整数表示答案。

input:

3
1 2
2 3
3 4

output:

2
3
4

• 对于第一组数据，\(n = 1, k = 2\)，\(T = \{0, 1\}\)，故答案为 \(2\)。
• 对于第二组数据，\(n = 2, k = 3\)，\(T = \{0, 1, 2\}\)，故答案为 \(3\)。
• 对于第三组数据，\(n = 3, k = 4\)，\(T = \{0, 1, 2, 3\}\)，故答案为 \(4\)。

对于所有数据，\(1 \le n, t \le 10 ^ 6\)，\(2 \le k \le 10 ^ 3\)。

很好的背包问题，但赛时没看出来，不够熟练。

我们发现如果数位出现了 \(0\) ，那么贡献就都变成了 \(0\)。

所以我们不考虑 \(0\)，在最后将答案 \(+1\) 即可。

因为对于 \(T\) 中的数，对于 \(k\) 进制下，可以分解为 \(\large \prod_{p_i \leq k} p_i^{c_i}\)，那么我们可以做一个完全背包。

首先，我们用ola筛 \(O(n)\) 筛质数，然后因为在 \(k\) 下，贡献是唯一确定的，考虑离线询问后按 \(k\) 分类。

然后枚举 \(k\)，来考究贡献。

我们对于每一个 \(n:1\sim N\)，都求一遍贡献。

设 \(f_i\) 为在当前进制下，\(n = i\) 时的方案数。

那么每当我们有一个 \(p_i \leq k\)，我们就做一遍完全背包，不断让他加入。

因为，我们在没有质数的时候，都可以用 \(1\) 填位，故 \(f\) 应初始化为 \(1\)。

AC-code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}
void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}
const int N = 1e6 + 5,K = 1e3+5,mod = 1e9 + 7;
bitset<K> isprime;
vector<int> p;
void init(){
    for(int i = 2;i<K;i++) {
        if(!isprime[i]) p.emplace_back(i);
        for(int j : p){
            if(i * j >= K) break;
            isprime[i * j] = true;
            if(i % j == 0) break;
        }
    }
    p.push_back(N);
}
vector<array<int,2>> q[K];
int ans[N],dp[N];

void add(int &a,int b) {
    a = (a + b);
    a >= mod ? a -= mod : a = a;
}

signed main() {
    init();
    int T = rd();
    for(int i = 1;i<=T;i++) {
        int n = rd(),k = rd();
        q[k].push_back({n,i});
    }
    int i = 0;fill(dp,dp + N,1);
    for(int k = 2;k < K;k++) {
        if(p[i] < k) {
            int r = p[i];
            for(int j = r;j < N;j++) add(dp[j],dp[j - r]);
            i++;
        }
        for(auto it : q[k]) add(ans[it[1]],dp[it[0]] + 1);
    }
    for(int i = 1;i<=T;i++) wt(ans[i]),putchar('\n');
	return 0;
}

Day5夜间场 送快递

题目描述

小 H 和小 S 打算合作送快递！

街道可以抽象成一条数轴，一开始小 H 和小 S 都在原点。
一共有 \(n\) 个时刻的快递任务，只有完成了前一个送快递任务才可以去完成下一个。

第 \(i\) 个时刻，小 H 和小 S 中的一个人要将快递送往位置 \(k_i\)，送完快递后，那个人>将停留在位置 \(k_i\)。

请问如何分配二人送快递的任务才能使得两人送快递走过的总路程之和最小？

输入格式

第一行一个 \(n\) 表示任务个数。

接下来一行 \(n\) 个整数表示 \(k_1\)，\(k_2\)，\(\cdots\)，\(k_n\)。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

5
4 6 3 4 7

样例输出 #1

11

提示

对于第一个样例，可以安排小 H 去送第 \(1,2,5\) 个时刻的任务，走过的总路程为
\(|4−0|+|6−4|+|7−6| = 7\)；

剩下的安排小 S 去送，走过的总路程为 \(|3−0|+|4−3| = 4\)。

二人走过的总路程为 \(11\)，可以证明这是最小的总路程。

数据范围

对于所有测试点，满足 \(1 \leq n \leq 10^6, 1 \leq k_i \leq 10^9\)。

测试点编号	\(n \leq\)	特殊性质
\(1,2,3,4\)	\(20\)	/
\(5,6\)	\(100\)	/
\(7,8,9,10\)	\(1000\)	/
\(11,12,13,14\)	\(10^5\)	/
\(15,16\)	\(10^6\)	\(1 \leq k_i \leq 50\)
\(17,18,19,20\)	\(10^6\)	/

原题的弱化版：[ARC073F] Many Moves

线段树优化 \(dp\)。

考虑写出 \(dp\) 及转移。

设 \(f_{i,j}\) 为小 H 停留在 \(i\) 处，小 \(S\) 停留在 \(j\) 处。

有：

\[f_{i,j} + \lvert s_{i + 1} - s_{i} \rvert \rightarrow f_{i + 1,j} \\ f_{i,j} + \lvert s_{i + 1} - s_{j} \rvert \rightarrow f_{i,i + 1} \\ \]

这个式子太混乱了，考虑重新设计 \(dp\)。

设 \(f_{i,j}\) 为右边的人停留在 \(i\) 处，左边的人停留在 \(j\) 处。

那么有：

\[f_{i,j} + \lvert s_{i + 1} - s_{i} \rvert \rightarrow f_{i + 1,j} \\ f_{i,j} + \lvert s_{i + 1} - s_{j} \rvert \rightarrow f_{i + 1,i} \\ \]

我们发现上面这个式子可以滚动，考虑优化后做扫描线。

\[f_{j} + \lvert s_{i + 1} - s_{i} \rvert \rightarrow f_{j} \\ f_{j} + \lvert s_{i + 1} - s_{j} \rvert \rightarrow f_{i} \\ \]

这个式子就可以用线段树维护了，因为我不想实现区间加，将 式1 考虑全局tag，对于式2，有：

\[f_{j} + \lvert s_{i + 1} - s_{j} \rvert - \lvert s_{i + 1} - s_{i} \rvert + \lvert s_{i + 1} - s_{i} \rvert \rightarrow f_{i} \\ \]

以下 \(v = f_{j} + \lvert s_{i + 1} - s_{j} \rvert - \lvert s_{i + 1} - s_{i} \rvert + \lvert s_{i + 1} - s_{i} \rvert\)

那么我们就可以用一个tag来完成区间加，然后对上式进行拆绝对值。

将 \(v\) 插入到线段树的 \(s_{i}\) 上，对于 \(s_{i + 1}\) 进行左右分讨即可，用两颗线段树就可以完成。

然后，最后用一颗线段树维护 \(f_{j}\) 即可，最后在这颗线段树上查一下，加上 \(tag\) AC。

AC-code:

#include<cstdio>
#include<cstring>
#include<ctype.h>
#include<algorithm>
using namespace std;
#define int long long
namespace FastIO {
	char buf[1 << 10], buf2[1 << 21], a[21], *p1 = buf, *p2 = buf, hh = ' ';
	int p, p3 = -1;
	void read() {}
	void print() {}
	inline int getc() {
		return p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 10, stdin), p1 == p2) ? EOF : *p1++;
	}
	inline void flush() {
		fwrite(buf2, 1, p3 + 1, stdout), p3 = -1;
	}
	inline void read(int &x) {
		x = 0;
		char ch = getc();
		while (!isdigit(ch)) {
			ch = getc();
		}
		while (isdigit(ch)) {
			x = (x << 1) + (x << 3) + (ch ^ '0');
			ch = getc();
		}
	}
	inline void print(int x) {
		if (p3 > 1 << 21) flush();
		if (x < 0) buf2[++p3] = '-', x = -x;
		do {
			a[++p] = x % 10 + 48;
		} while (x /= 10);
		do {
			buf2[++p3] = a[p];
		} while (--p);
		buf2[++p3] = hh;
	}
}
#define read FastIO::read
#define print FastIO::print
const int N = 1e6+5,inf = 1e18;
int n,a[N],st[N],top;
int tag;

inline int min(int x,int y) {
	return x > y ? y : x;
}

struct sgt{
#define mid ((pl + pr) >> 1)
int val[N << 2];
#define ls (p << 1)
#define rs (ls | 1)
inline sgt(){memset(val,0x3f,sizeof(val));}

inline void push_up(int p){
    val[p] = min(val[ls],val[rs]);
}

void update(int p,int pl,int pr,int k,int d) {
    if(pl == pr) {
        val[p] = min(d,val[p]);
        return;
    }
    if(k <=  mid) update(ls,pl,mid,k,d);
    else update(rs,mid+1,pr,k,d);
    push_up(p);
}

int query(int p,int pl,int pr,int l,int r) {
    if(!p) return inf;
    if(l <= pl && pr <= r) return val[p];
    if(r <= mid) return query(ls,pl,mid,l,r);
    else if(l > mid) return query(rs,mid+1,pr,l,r);
    else return min(query(rs,mid+1,pr,l,r),query(ls,pl,mid,l,r));
}
}T[3];

signed main() {
   	read(n);
    for(int i = 1;i<=n;i++) read(a[i]);
    for(int i = 1;i<=n;i++) st[++top] = a[i];
    st[++top] = 0;
    sort(st + 1,st + top + 1);
    top = unique(st + 1,st + top + 1) - st - 1;
    for(int i = 1;i<=n;i++) a[i] = lower_bound(st + 1,st + top + 1,a[i]) - st;
    T[0].update(1,1,top,1,0);T[1].update(1,1,top,1,0);
    for(int i = 1;i<=n;i++) {
        int c = T[0].query(1,1,top,1,a[i]) + st[a[i]];
        c = min(c,T[1].query(1,1,top,a[i],top) - st[a[i]]);
		tag += abs(st[a[i]] - st[a[i - 1]]);
        T[2].update(1,1,top,a[i - 1],c - abs(st[a[i]] - st[a[i - 1]]));
        T[0].update(1,1,top,a[i - 1],c - st[a[i - 1]] - abs(st[a[i]] - st[a[i - 1]]));
        T[1].update(1,1,top,a[i - 1],c + st[a[i - 1]] - abs(st[a[i]] - st[a[i - 1]]));
    }
    print(T[2].query(1,1,top,1,top) + tag);
    FastIO::flush();
	return 0;
}

Day7 安全点

在遥远的企鹅Land，企鹅们居住在一个由相互连接的冰块组成的广阔大陆中，这个大陆呈现为一棵树形结构。冰块之间通过坚固的冰桥相连，每座冰桥都有一个权重，代表穿越它的距离。企鹅们对探索这片寒冷之地充满热情，他们采用了一种独特的深度优先搜索方法来标记冰块，从冰块1开始。这种方法确保了每块冰块按照特定顺序被访问，使得企鹅们的导航更加轻松。

出门在外，要注意安全。因为冰川经常容易出现雪崩的情况，所以企鹅国王让企鹅们修建了很多安全区。修建安全区的时候，企鹅主管非常相信企鹅风水学，他决定在编号含有11的冰块上修建安全区，这样可以让避难的企鹅尽可能幸运。

豆豆是一只充满好奇心的探险家企鹅，他经常需要前往最近的安全点——即编号含有11的冰块，非常适合极端天气下休息和聚会。

因为时探险家，所以豆豆有一系列任务需要完成：对于每个任务，他希望找到从当前所在冰块到任何安全点的最短路径，并且这些安全点的编号在指定的范围内（因为他相信这些范围里的更安全，比如从111到1111）。

你将获得大陆冰块的结构，这是一棵加权树。树的节点代表冰块，边代表带有相应权重的冰桥。冰块已经被深度优先遍历算法从冰块1开始编号。

豆豆需要你的帮助来完成 \(q\) 个任务。每个任务由三个整数组成：

• \(s\)：豆豆当前所在的冰块编号。
• \(L\) 和 \(R\)：豆豆感兴趣的安全点编号范围。

对于每个任务，你需要确定从冰块 \(s\) 到任何安全点的最短距离，这些安全点的编号在 \(L\) 和 \(R\) 之间（包括 \(L\) 和 \(R\)）。

从文件 ice.in 中读入数据。

第一行包含两个整数 \(n\) 和 \(q\) —— 冰块的数量和任务的数量。

接下来的 \(n-1\) 行描述了冰桥。每行包含两个整数 \(u_i\) 和 \(d_i\)，表示冰块 \(u_i\) 和 \(i\) 之间的冰桥，距离为 \(d_i\)。

接下来的 \(q\) 行描述了任务。每个任务包含三个整数 \(s_i\)、\(L_i\) 和 \(R_i\)，表示任务的参数。保证至少有一个安全点的编号 \(z\) 满足 \(L_i \leq z >\leq R_i\)。

输出到文件 ice.out 中。

对于每个任务，输出从指定冰块 \(s\) 到给定范围内任何安全点的最短距离。

input:

11 5
1 9
2 9
3 3
4 7
5 7
5 2
4 8
8 7
4 2
3 6
4 5 11
11 11 11
10 11 11
3 9 11
1 10 11

output:

9
0
11
6
24

• 对于前 10% 的数据，\(n, q \leq 20\)；
• 对于前 20% 的数据，\(n, q \leq 1000\)；
• 对于另外 15% 的数据，\(q = 1\)；
• 对于另外 15% 的数据，\(L = 1, R=n\)；
• 对于前 90% 的数据，\(n, q \leq 100000\)；
• 对于前 100% 的数据，\(n, q \leq 1000000, 0 \leq d_i \leq 10^9\)。

将换根和线段树操作结合到一起，很妙的思路。

我们可以通过 \(O(n)\) 的方式，将根所达的 \(dis\) 计算出来。

然后我们考虑换根，对于一次换根，我们会让进入的子树内的距离减去 \(w_{u \rightarrow v}\)。

每一个不进入的子树，距离加上 \(w_{u \rightarrow v}\)。

然后对于离线的询问，考虑区间查询最小值。

然后本题就做完了。

\(Warning\)：本题数据会超过 \(10^{18}\)

AC-code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}
inline void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}
const int N = 2e6+5,inf = 0x3f3f3f3f3f3f3f3fll;
int n,qy;
vector<array<int,2>> g[N];
vector<array<int,3>> q[N];
inline void add(int u,int v,int w){g[u].push_back({v,w});}
int siz[N],dep[N],A[N],L[N],R[N],cnt;
void dfs1(int x,int fa) {
	siz[x] = 1;
	L[x] = ++cnt;
	for(auto it : g[x]) {
		int y = it[0],W = it[1];
		if(y == fa) continue;
		dep[y] = dep[x] + W;
		dfs1(y,x);
		siz[x] += siz[y];
	}
	R[x] = L[x] + siz[x] - 1;
}
int tar[N];
namespace sgt{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)
int mn[N<<2],tag[N<<2];
void push_up(int p) {
	mn[p] = min(mn[ls],mn[rs]);
}

void addtag(int p,int d) {
	tag[p] += d;
	mn[p] += d;
}

void push_down(int p) {
	if(tag[p]) {
		addtag(ls,tag[p]);
		addtag(rs,tag[p]);
		tag[p] = 0;
	}
}

void build(int p,int pl,int pr) {
	tag[p] = 0;
	if(pl == pr) {mn[p] = tar[pl];return;}
	build(ls,pl,mid);
	build(rs,mid+1,pr);
	push_up(p);
}

void update(int p,int pl,int pr,int l,int r,int d) {
	if(l <= pl && pr <= r) {addtag(p,d);return;}
	push_down(p);
	if(l <= mid) update(ls,pl,mid,l,r,d);
	if(r > mid) update(rs,mid+1,pr,l,r,d);
	push_up(p);  
}

int query(int p,int pl,int pr,int l,int r) {
	if(l <= pl && pr <= r) return mn[p];
	push_down(p);
	int res = inf;
	if(l <= mid) res = min(res,query(ls,pl,mid,l,r));
	if(r > mid) res = min(res,query(rs,mid+1,pr,l,r));
	return res;
}
}

void dfs2(int x,int fa) {
	for(auto &it : q[x]) {
		int l = it[0],r = it[1],id = it[2];
		A[id] = sgt::query(1,1,n,l,r);
	}
	for(auto &it : g[x]) {
		int y = it[0],w = it[1];
		if(y == fa) continue;
		sgt::update(1,1,n,L[y],R[y],-(w<<1));
		sgt::update(1,1,n,1,n,w);
		dfs2(y,x);
		sgt::update(1,1,n,L[y],R[y],(w<<1));
		sgt::update(1,1,n,1,n,-w);
	}
}

bitset<N> _11;

signed main() {
	freopen("ice.in","r",stdin);
	freopen("ice.out","w",stdout);
	n = rd(),qy = rd();
	for(int i = 1;i<=n;i++) _11[i] = _11[i / 10] || (i % 100 == 11);
	for(int i = 2;i<=n;i++) {
		int u = rd(),v = i,w = rd();
		add(u,v,w);add(v,u,w);
	}
	for(int i = 1;i<=n;i++) sort(g[i].begin(),g[i].end());
	for(int i = 1;i<=qy;i++) {
		int u = rd(),l = rd(),r = rd();
		q[u].push_back({l,r,i});
	}
	dfs1(1,0);
	for(int i = 1;i<=n;i++) 
		if(_11[i]) tar[i] = dep[i];
		else tar[i] = inf;
	sgt::build(1,1,n);
	dfs2(1,0);
	for(int i = 1;i<=qy;i++) wt(A[i]),putchar('\n');
	return 0;
}

2024/11/27

最后一场比赛，终于 AK 了

Day8 奖励题

企鹅豆豆帮助企鹅国完成了一系列工程重大建设规划，因此企鹅国王打算奖励企鹅豆豆一些奖金。

但是自然玩过很多抽卡游戏的企鹅国王，不希望这个奖金如此的平淡。于是他命人打造了一个 A 面骰子和一个 B 面骰子，每个骰子都会等概率丢出 \(1\) 到 \(x\) （x是面数）之间的数。

现在，企鹅国王说，企鹅豆豆来丢一遍骰子，丢出来的数字 A 和 B 的异或值，就是企鹅豆豆的奖金。

现在企鹅豆豆想知道所有可能的情况下，这个奖金的总和是多少？

从文件 free.in 中读入数据。

第一行包含两个整数 \(A\) 和 \(B\)。

输出到文件 free.out 中。

输出一行一个数，表示所有情况下的奖金的总和。

input1:

1 2

output1:

3

input2：

2 3

output2:

9

input3:

5 5

output3:

84

考虑对于 \(a_i:1\sim a\)，每一位与可能的 \(b\) 产生的贡献。

直接桶计数，然后枚举 \(a\) 即可。

#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}
void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}
int a,b,c[25][2];
signed main() {
	freopen("free.in","r",stdin);
	freopen("free.out","w",stdout);
	a = rd(),b = rd();
	int ans = 0;
	if(a > b) swap(a,b);
	for(int i = 0;i<=20;i++)
		for(int j = 1;j<=b;j++)
			c[i][(j >> i) & 1]++;
	for(int i = 1;i<=a;i++)
		for(int j = 0;j<=20;j++)
			ans += c[j][!((i >> j) & 1)] * (1<<j);
	wt(ans);
	return 0;
}

Day8 计数题

在遥远的企鹅国度Penguinland，豆豆企鹅对冰雪覆盖的湖面上出现的神秘魔法序列产生了浓厚的兴趣。这些序列可以被看作是一系列数字的排列，\(0\) 到 \(n-1\) 每个数字恰好都出现了一次。

经过多年打表和找规律的经验，豆豆企鹅注意到，当这个序列 \(a_1, a_2, \dots, a_n\) 满足如下规律时，第二天钓鱼就不会空军！

1. 每个数字仅出现过一次。
2. 这些数字都在 \([0, n-1]\) 之间。
3. 对于每个 \(i(3 \leq i)\)，满足 \((a_i - a_{i-1})\times(a_{i-1} - a_{i-2}) < 0\)。也就是说，相邻数字的大小关系要和前一个相邻的大小关系不一样。

但是由于冰面上被大雪覆盖，所以只能看到魔法序列的一部分开头 \(S=\{S_1, S_2, \cdots, S_m\}\)。

你的任务是帮助豆豆企鹅计算——所有以给定起始序列 \(S\) 开始的不空军序列的数量，并返回这个数量对 \(10^9 + 9\) 取模的结果。

从文件 seq.in 中读入数据。

第一行包含两个整数 \(n\) 和 \(m\)，表示序列的总长度以及 \(S\) 的长度。

第二行包含 \(m\) 个整数，表示 \(S\)。

输出到文件 seq.out 中。

输出一个整数，表示以给定起始序列 \(S\) 开始的魔法序列的数量对 \(10^9 + 9\) 取模的结果。

input1：

3 2
1 1

output1:

0

input2:

2 0

output2:

2

input3:

3 1
1

output3:

2

很好的计数题。

首先特判。

我们考虑设 \(f_{i,j,k,0/1}\) 为当枚举到 \(i\) 时，后面有 \(j\) 个数 \(\leq x_i\)，有 \(k\) 个数 \(> x_i\)，且上一次为 \(>\) / \(<\)。

显然，时间复杂度 \(\mathcal{O}(n^4)\)，显然不可过。

考虑状态优化，我们每次只考虑相对排名，所以排名总数是不变的。

所以我们可以通过 \(n - i + 1 - j\) 得到比他大的数。

所以，我们可以省略掉 \(k\) 这一维。

而我们每次在 \(i\) 处取 \(x_i\) ，那么，我们其实可以根据排名来推断下一个选择的数 \(x_{i + 1}\) 与 \(x_i\) 的大小。

那么，我们有转移：

\[f_{i,j,0} \rightarrow^{k \leq j} f_{i,k,1} \\ f_{i,j,1} \rightarrow^{k > j} f_{i,k,0} \]

这样就是 \(\mathcal{O}(n ^ 3)\)。

还不够优秀！！！

我们发现，计数是连续的。

所以，我们考虑前缀和优化，将上一次的计数加入前缀和。

然后对初始状态做一下初始化即可。

AC-code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}
void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}
const int N = 5005,mod = 1e9 + 9;
int n,m,a[N],b[N],rnk[N];
int f[N][N][2],add[N][2];
bitset<N> vis;
signed main() {
	freopen("seq.in","r",stdin);
	freopen("seq.out","w",stdout);
	n = rd(),m = rd();
	for(int i = 1;i<=m;i++) a[i] = rd() + 1;
	for(int i = 2;i<=m;i++) b[i] = a[i] - a[i - 1];
	for(int i = 2;i<=m;i++) if(!b[i]) {puts("0");return 0;}
	for(int i = 3;i<=m;i++) if(b[i] * b[i - 1] >= 0) {puts("0");return 0;}
	for(int i = 1;i<=m;i++) {
		if(vis[a[i]]) {
			puts("0");
			return 0;
		}else vis[a[i]] = true;
	}
	if(m == 0) {
		for(int i = 1;i<=n;i++) 
			f[1][i][0] = f[1][i][1] = 1;
		m = 1;
	}else if(m == 1) {
		for(int i = 1;i<a[1];i++) 
			f[1][i][0] = 1;
		for(int i = a[1] + 1;i <= n;i++)
			f[1][i - 1][1] = 1;
	}
	else {
		int cnt = 0;
		for(int i = 1;i<=n;i++)
			if(!vis[i] || i == a[m])
				rnk[i] = ++cnt;
		int fg = (b[m] < 0) ? 0 : 1; 
		f[m][rnk[a[m]]][fg] = 1;
	}
	for(int i = m + 1;i<=n;i++)
	{
		for(int j=1;j<=n-i+2;j++)
		{
			add[j][0]=add[j-1][0]+f[i-1][j][0];
			add[j][1]=add[j-1][1]+f[i-1][j][1];
			add[j][0]%=mod;
			add[j][1]%=mod;
		}
		
		for(int j=1;j<=n-i+1;j++)
		{
			f[i][j][1]+=add[j][0];
			f[i][j][1]%=mod;
			f[i][j][0]+=(add[n-i+2][1]-add[j][1]+mod)%mod;
			f[i][j][0]%=mod; 
		}
	}
	wt((f[n][1][1] + f[n][1][0]) % mod);
	return 0;
}

Day8 异或题

在异或企鹅国，音乐节是企鹅们最热衷的活动之一。最近，企鹅豆豆凭借其经典歌曲《企鹅也会异或》再次成为音乐节的焦点，这距离他上次获得这一荣誉已有两年半。为了更好地了解企鹅歌曲在音乐节中的影响力，我们设计了一个统计问题。

我们希望了解在特定时间段内，哪些歌曲最受欢迎。一个简单但有效的衡量方法是统计歌曲在某个时间段内首次和最后一次成为最受欢迎歌曲的时间间隔。时间间隔越长，歌曲在该时>间段内的影响力就越大。

企鹅音乐史一共有 \(N\) 天(从第\(0\)天开始)，每天都有一个歌曲 \(S_i\) 是当天的最火的歌曲。

给定一个区间 \([A, B]\) 和一个企鹅歌曲 \(x\)，歌曲 \(x\) 在该区间内的影响力为最早的出现位置下标 \(t_0\) XOR 最晚出现下标 \(t_1\)。这里的 XOR 指的是异或操作。

注意，如果一个歌曲只出现了一天，那么显然 \(t_0\ XOR\ t_0 = 0\)。

这天企鹅豆豆在学校讲音乐史，有很多小企鹅对于音乐史有很多问题，大家都想知道自己关心的时间内，自己的歌曲有多火。

由于问题太多了，所以企鹅豆豆只能回答，在历史 \([A_i, B_i]\) 期间，每个企鹅歌曲各自的火热程度的异或和。（这里不是求和而是异或和，因为这里是异或企鹅国。）

也就是说你需要写个程序，对于每个区间，输出一个正整数，表示该区间内所有企鹅歌曲的影响力的异或和。

从文件 xor.in 中读入数据。

第一行包含两个正整数 \(N\) 和 \(Q\)，分别表示周期长度和区间个数。

接下来一行，包含 \(N\) 个正整数，表示每天最受欢迎的演奏者的编号ID （\(1\leq ID \leq N\)）。

接下来 \(Q\) 行，每行包含两个非负整数 \(A_i\) 和 \(B_i\) (\(A_i \leq B_i\))，表示区间的左右端点。

输出到文件 xor.out 中。

输出 \(Q\) 行，每行一个非负整数，表示每个区间内的影响力的异或和。

input1:

5 3
1 2 1 3 2
0 2
1 3
0 4

output2：

2
0
7

想到了反悔贪心。

先离线询问，做扫描线。

我们考虑将 \(lst_{a_i}\) 记录下来。

我们每次将 \(i\) 和 \(lst_{a_i}\) 的贡献插入到 \(lst_{a_i}\)，然后直接做一次区间异或和。

为什么这样是对的呢？

因为我们在扫描线的时候，会将 \(i \oplus lst_{a_i}\) 插入到 \(lst_{a_i}\)，而将 \(lst_{a_i} \oplus lst_{lst_{a_i}}\)（上一次进行操作） 插入到 \(lst_{lst_{a_i}}\)。

当我们查询 \(l \leq lst_{lst_{a_i}}\) 的时候，由于异或的自反性，我们中间插入的值都会抵消掉，只留下第一个和最后一个，所以一定是正确的。

用线段树维护即可。

AC-code：

#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}
void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}
const int N = 1e6+5;
int n,qy,a[N];
vector<array<int,2>> q[N];

namespace sgt{
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((pl + pr) >> 1)
int x[N<<2];
void push_up(int p) {
	x[p] = x[ls] ^ x[rs];
}

void update(int p,int pl,int pr,int k,int d) {
	if(pl == pr) {
		x[p] ^= d;
		return;
	}
	if(k <= mid) update(ls,pl,mid,k,d);
	else update(rs,mid+1,pr,k,d);
	push_up(p);
}

int query(int p,int pl,int pr,int l,int r) {
	if(l <= pl && pr <= r) return x[p];
	if(r <= mid) return query(ls,pl,mid,l,r);
	else if(l > mid) return query(rs,mid+1,pr,l,r);
	else return query(ls,pl,mid,l,r) ^ query(rs,mid+1,pr,l,r);
}

}
int lst[N],ans[N];
signed main() {
	freopen("xor.in","r",stdin);
	freopen("xor.out","w",stdout);
	n = rd(),qy = rd();
	for(int i = 0;i<n;i++) a[i] = rd();
	for(int i = 1;i<=qy;i++) {
		int l = rd(),r = rd();
		q[r].push_back({l,i});
	}
	memset(lst,-1,sizeof(lst));
	for(int i = 0;i<n;i++) {
		if(~lst[a[i]]) sgt::update(1,0,n - 1,lst[a[i]],i ^ lst[a[i]]);
		lst[a[i]] = i;
		for(auto it : q[i]) {
			int l = it[0],r = i,id = it[1];
			ans[id] = sgt::query(1,0,n - 1,l,r);
		}
	}
	for(int i = 1;i<=qy;i++) wt(ans[i]),putchar('\n');
	return 0;
}

2024/11/29

NOIP 2024 rp++!

加油！