P10394 接连不断！题解

P10394 接连不断！

1.分析

感谢 学长 ckain 的 hint

对于任意一个图的某一个点，只能向外连一条无向边 即 \(i \Rightarrow (i \cdot x) mod\ n\)

---

推论 \(1\) ：
不难发现：任意一个图，\(0\) 号位只能指向它自己

---

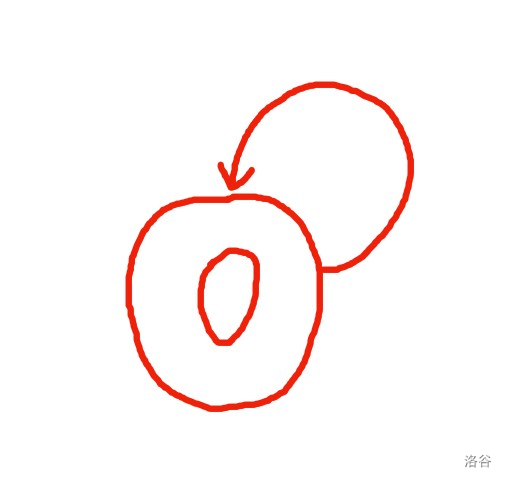
推论 \(2\) ：
如果在一个图中存在两个环及以上，则必然不连通

举个简单的例子，如图

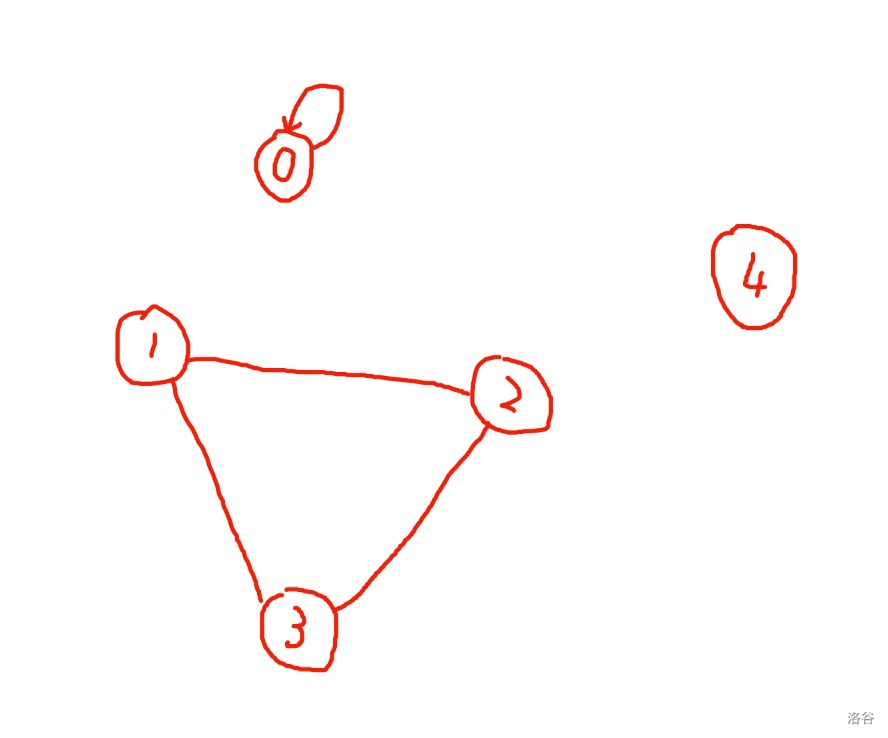
\(4\) 号点只能连两个环中之一

---

综合两个推论，可以发现：若将所连的边（即 \(i \Rightarrow (i \cdot x) mod\ n\)）看做有向边，则连通图一定是 内向基环树

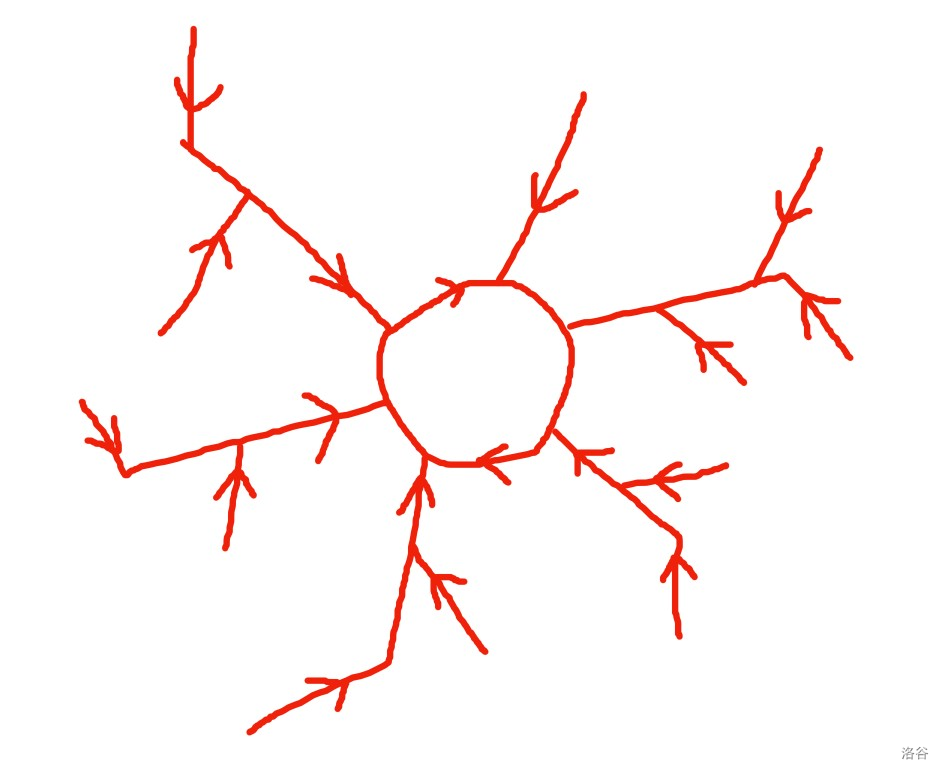
其中 \(0\) 号位 一定是一个自环，故连通图中所有点一定与 \(0\) 号位 连通

所以，对于每一个点,若 存在一个 \(k\)，使得 \((i \cdot x ^ k)\ mod\ n = 0\) 就肯定与 \(0\) 号位 连通

那么对于一个连通图，其中每个点都要和 \(0\) 号位相连，只有 $ n | x ^ k$ 时成立

那么，\(x\) 必须为 \(n\) 的所有素因子的乘积 的 \(y\) 倍

证明: 令 $n = \prod_{i} p_i ^ {k_i} (k \in \mathbb{N} , p \in \mathbb{P}) $，则对于 \(x = \prod_{i} p_i\) 必然存在一个 \(k^{\prime} = \max{k_i}\)，使得 $ n | x^{k{\prime}}$ ， 自然 \(n | y \cdot x^{k^\prime} (y \in \mathbb{N})\)

最后只需找出循环节 \(x\) 即可

---

2.行动

对 \(n\) 进行素因子分解，求得循环节长度 \(len\)
因为图是从 \(0\) 开始编号，在 \(m / len\) 后还需 \(+1\)

\(code\) :

#include <bits/stdc++.h>
using namespace std;

#define int long long

namespace my{

CIN N = 1e6+5;
int n,m,T,ans;
int p[N],c[N],t;

void pm(int num){
	t = 0;
	for(int i = 2;i<= sqrt(num);i++) 
		if(num % i == 0) {
			p[++t] = i;c[t] = 0;
			while(num % i == 0) c[t]++,num/=i;
		}
	if(num > 1) p[++t] = num,c[t] = 1;
}

int check(int num){
	int res = 1;
	for(int i = 1;i<=t;i++) res *= p[i];
	return res;
}

signed main(){
	speed_up(true);
	
	cin>>T;
	while(T--) {
		cin>>n>>m;
		pm(n);
		int len = check(n);
		ans = m / len + 1;
		cout<<ans<<'\n';
	}

	return 0;
}

}

signed main() {
	return my::main();
}