浅谈拓扑排序
总目录
〇. 附录
Ⅰ. 定义
Ⅱ. 步骤
Ⅲ. 更新日志
〇. 附录
啊,在开始写总结之前我们先讲个故事
我们可以拿大学选课的例子来描述这个过程,比如学习大学课程中有:$ D \(学科,\) X \(学科,\) L \(学科,\) G \(学科与\) T \(学科,\) Y \(学科,\) S \(学科,\) J \(学科。当我们想要学习\) S $学科的时候,就必须先学会 $ L $学科 和 $ G \(学科与\) T $学科,不然在课堂就会听的一脸懵逼。当然还有一个更加前的课程 $ D $学科。这些课程就相当于几个顶点 $ u $ , 顶点之间的有向边 $ (u,v) $就相当于学习课程的顺序。显然拓扑排序不是那么的麻烦,不然你是如何选出合适的学习顺序。下面将介绍如何将这个过程抽象出来,用算法来实现。
如果有一天,老师说想要学习 $ S $ 学科,还得先学 $ J $学科,而 $ J $学科 的前置课程又是 $ S $学科。
然后你就,
我到底应该先学哪一个?当然我们在这里不考虑什么同时学几个课程的情况。在这里,$ S $学科 和 $ J $学科 间就出现了一个环,显然你现在没办法弄清楚你需要学什么了,于是你也没办法进行 拓扑排序 了。因而如果有向图中存在环路,那么我们没办法进行 拓扑排序 了。
Ⅰ. 定义
| 中文名 | 拓扑排序 |
|---|---|
| 英文名 | topsort |
| 应用学科 | 计算机科学 图论 |
| 图 | 有向无环图 |
在图论中,拓扑排序(Topological Sorting)是一个有向无环图(DAG)(DAG与拓扑排序的互相限制关系在链接中)
也就是这些顶点按照某种特定的优先关系进行排序,排成线性序列的过程叫做拓扑排序。
且此序列要满足一下两个要求:
\(1.\) 每个顶点出现且只出现一次。
\(2.\) 若存在一条从顶点 \(A\) 到顶点 \(B\) 的路径,那么在序列中顶点 \(A\) 出现在顶点 \(B\) 的前面。
接下来我们就来看一下拓扑排序步骤。
Ⅱ. 步骤
简而言之
\(First.\) 先从一个有向无环图中找出一个入度为0的点输出,然后从此图中,将其点删除,同时将以它为起点的边,即此点所有的出度的边全部删除,这个步骤简称为 删点断边
\(Next.\) 重复第一条操作,直到有向无环图中无点(即完成拓扑排序) \(or\) 当前的图中不存在入度为0的点了(即此图是一个有向有环图,也就是必然存在环),简称为 输出判环
了解了这个,那我们就来实践一下,如图。
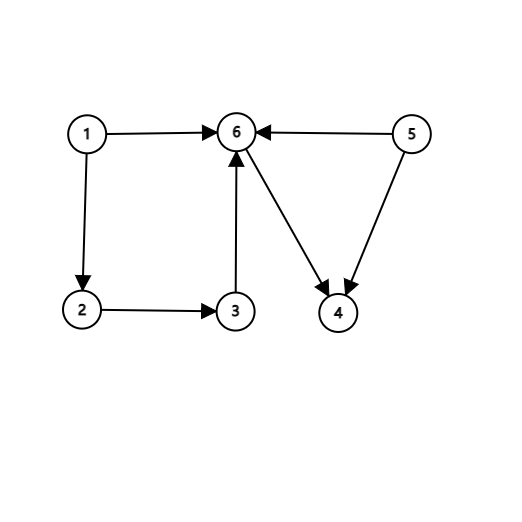
这是一个有向无环图。
答案很明显,输出结果是 \(\Big\{1,2,3,5,6,4\Big\}\)
步骤如下:
\(1.\) 删去入度为\(0\)的点\(1\),且将其作为起点的边同时删去,并输出 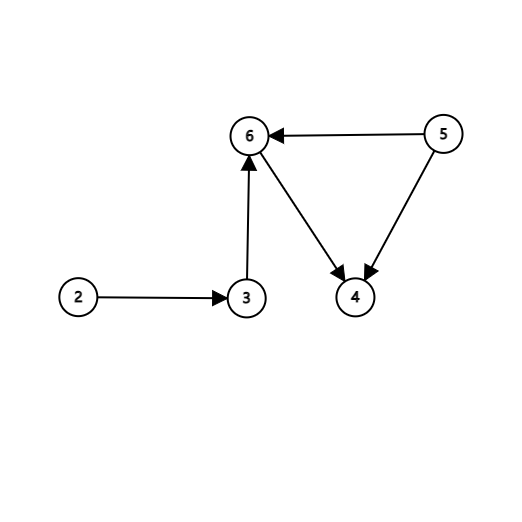
\(2.\) 删去入度为\(0\)的点\(2\),且将其作为起点的边同时删去,并输出 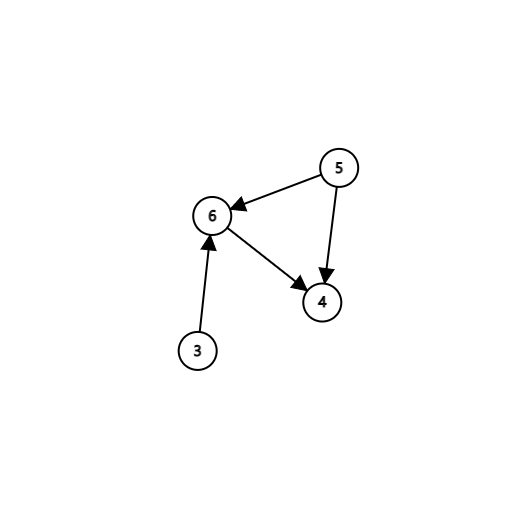
\(3.\) 删去入度为\(0\)的点\(3\),且将其作为起点的边同时删去,并输出 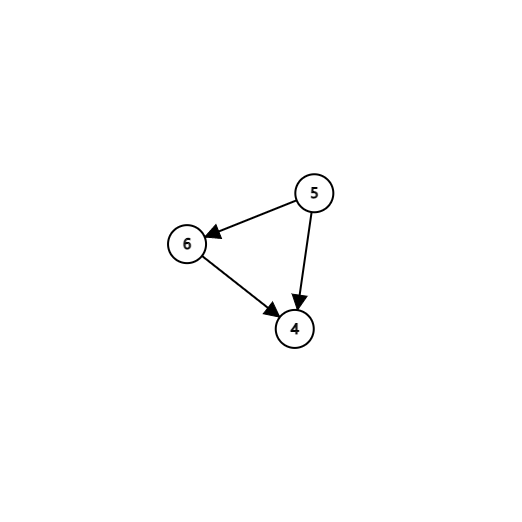
\(4.\) 删去入度为\(0\)的点\(5\),且将其作为起点的边同时删去,并输出 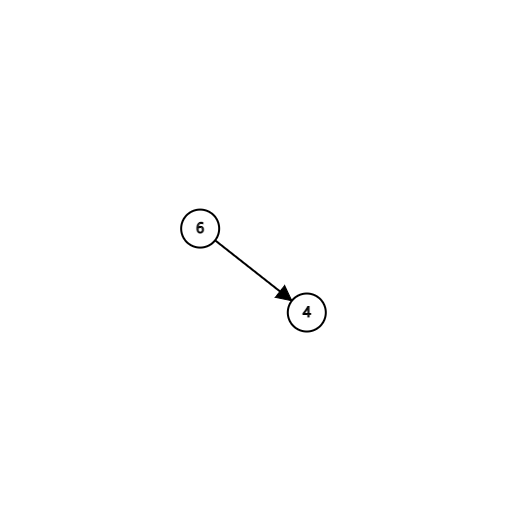
\(5.\) 删去入度为\(0\)的点\(6\),且将其作为起点的边同时删去,并输出 
最后就直接输出最后的点\(4\)
于是我们就可以敲出骗分版代码了(也不知道是多久打的了,但是这个代码有个极大的\(bug\),就是不能判断环,本人正在努力理解史前代码,试图修改)
#include <cstdio>
#include <algorithm>
#define N 205
using namespace std;
struct top {int to,Next;}g[N*20];
struct SORT {int now,Rdnum;}flag[N];
int n,m,x[N],y[N],cnt,h[N],rd[N],zdian[N],ans[N];
int nt,nt1;
int main() {
scanf("%d %d",&n,&m);
for (int i=1;i<=m;i++) {scanf("%d %d",&x[i],&y[i]); rd[y[i]]++;}
for (int i=1;i<=n;i++) {
if (rd[i]==0) {
nt++;
ans[i]=i;
}
else {
nt1++;
flag[i].now=i;
flag[i].Rdnum=rd[i];
}
}
for (int i=1;i<=n;i++) {
if (ans[i]) printf("%d ",ans[i]);
}
for (int i=1;i<=n;i++) {
if (flag[i].now) printf("%d ",flag[i].now);
}
}
好吧,下面贴出容易理解的代码(正码)
#include <bits/stdc++.h>
using namespace std;
const int maxx = 1001;
int n , m;
int rd[maxx] , Ans[maxx] , a[maxx][maxx] , v[maxx];
void Read() {
scanf("%d %d",&n,&m);
for (int i=1 , x , y; i<=m; i++ ) {
scanf("%d %d",&x,&y);
a[x][y] = 1;
rd[y]++ ;//入度计数
}
}
int Tsort() {
for (int i=1;i<=n;i++) {
int j=1; //从第一个点开始查找
while (j<=n&&rd[j]) j++;//寻找入度为0的点
if (j>n) return 0;
Ans[++Ans[0]] = j;
rd[j]=-1;
for (int k=1;k<=n;k++) {
if (a[j][k]) rd[k]--;//断开与j相连的边
}
}
return 1;//这是判断是否有环
}
int main() {
Read();
if (Tsort()) {
for (int i=1; i<=Ans[0]; i++ ) {
printf("%d ",Ans[i]);
}
}
else printf("no solution");
return 0;
}
看懂了上面的模板代码,我们可以进一步拓展。
对一个有向图 进行拓扑排序,是将 G 中所有顶点 排成一个线性序列,使得图中任意一对顶点 u 和 v,若 ∈E(G),则 u 在线性序列中出现在 v 之前。若图中存在有向环,则不可能使顶点满足拓扑次序。
【输入格式】
第$ 1 \(行\):2 \(个空格分开的整数\) n \(和\) m $,分别表示图的顶点数和边数。 第 \(2.m+1\) 行:每行$ 2 \(个空格分开的整数\) i,j,i \(表示一条边的起点,\)j$ 表示终点。
【输出格式】
拓扑序,顶点从$ 1 $开始编号,如果有多个拓扑序,则顶点编号 大 的优先输出。
有环输出:\(no\) \(solution\)
【输入样例 \(1\)】
\(4\) \(4\)
\(1\) \(3\)
\(1\) \(4\)
\(2\) \(3\)
\(2\) \(4\)
【输出样例$ 1 $】
\(2\) \(1\) \(4\) \(3\) (对于$ 1 \(和\) 2 \(两个点都是初始入度为\) 0 \(的点,选择编号大的\) 2 $优先输出)
【输入样例$ 2 $】
\(4\) \(4\)
\(1\) \(2\)
\(2\) \(3\)
\(3\) \(4\)
\(4\) \(1\)
【输出样例$ 2 $】
\(no\) \(solution\)
【数据范围】 100%的数据满足:1≤n≤200,1≤m≤20000,邻接矩阵即可实现。
题目完
分析:其实这道题既然要让我们,以顶点编号 大 的优先输出。其实只需要把模板里面的
while (j<=n&&rd[j]) j++;
改成
while(rd[j]&&j>=1) j--;
就完了
代码如下
#include<cstdio>
#include<iostream>
using namespace std;
bool f[201][201];int x,y,n,m,j,rd[201],a[201];
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++) scanf("%d %d",&x,&y),f[x][y]=1,rd[y]++;
for(int i=1;i<=n;i++){
j=n;
while(rd[j]&&j>=1) j--;
if(j==0) { printf("no solution");return 0; }
a[++a[0]]=j;rd[j]=-1;
for(int k=1;k<=n;k++)
if(f[j][k]) rd[k]--;
}
for(int i=1;i<=a[0];i++) printf("%d ",a[i]);
}
懂了这些,你就可以去做这道题了【持续更新】
您也可以在luogu找到这篇文章


 浙公网安备 33010602011771号
浙公网安备 33010602011771号