单调队列/斜率优化DP及训练18题题解

单调队列优化DP

其实就是解决一些取一个区间内的最小值的转移。

转移的一般步骤

1.弹掉队列尾部所有不如\(f_{i-1}\)的东西。
2.将\(f_{i-1}\)加入队首。
3.弹掉队列头所有不可用的东西。
4.计算\(f_i\)。

其实写多了有手感之后就不是很难。

A.「一本通 5.5 练习 1」烽火传递

设\(f_i\)为以i为结尾，1到i全部可行且i必点烽火的时候的最小花费。转移就是从\([i-m,i-1]\)一段来转，非常容易用单调队列优化。

B.绿色通道

发现可以二分答案，然后烽火传递即可。

C.「一本通 5.5 例 2」最大连续和

搞出前缀和，然后还是从\([i-m,i-1]\)一段来转移。

D.[USACO Open11] 修剪草坪

让选中的连续段长度不超过k，就是求一个空段长度不超过k的，再用总和减去。然后烽火传递。

E.[Scoi2010]股票交易

首先，对于这种比较复杂的DP，先设出状态：\(f_{i,j}\)为前i天，这一天交易完之后还剩下j股时最大收益。
有这么四种转移：

1.全部重新买

\(f_{i,j}=-ap_i * j\)，比较显然。

2.不买也不卖

\(f_{i,j}=f_{i-1, j}\)。

3.在之前的基础上买

容易发现，我们从\(i\in [1,i-w-1]\)都可以转移过来，但是最优值肯定是在i-w-1处取得。
\(f_{i,j}=f_{i-w-1,k} - (j-k) * ap_i\)且\(j-as_i \le k < j\)。

4.在之前的基础上卖

与3基本相同。
\(f_{i,j}=f_{i-w-1,k} + (k-j) * bp_i\)且\(j < k \le j + bs_i\)。
此时我们在转移3、4两类时，以3为例，就按顺序把i-w-1处的\(f_{i-w-1,k} + k * ap_i\)塞进单调队列，并维护滑动窗口。4同理，需要倒序。

F.[NOI2005] 瑰丽华尔兹

这一类题一般是要把当前是第几个时间段的结尾设进去。
设\(f_{i,j,k}\)为第i个时间段结尾，目前在\((j,k)\)的最大滑动距离。
转移的话就是看当前这个时间段往哪边滑，就从它的相反方向转移，单调队列把每一行/列一转移即可。顺便滚动数组优化空间。

G.「acwing298」围栏

设\(f_{i,j}\)为刷到第i个工匠，第j块木板时最大收益，不要求刷了这个工匠或这个木板。

1.该工匠不刷

\(f_{i,j} = f_{i-1,j}\)。

2.该工匠刷

\(f_{i,j} = f_{i-1,k} + (j-k) * P_i\)，其中\(S_i \le j \le S_i + L_i - 1\)，\(j - L_i \le k \le S_i - 1\)。

3.该木板不刷

\(f_{i,j} = f_{i,j-1}\)。
是一个比较好想的单优DP。

H.「acwing299」裁剪序列

这个比较困难。
先想一个朴素DP：
\(f_i = min\{f_j + max\{a_{j+1}, a_{j+2}, \cdots a_i\}\}\)
倒着枚举j，转移的复杂度是\(n^2\)的。根据式子分析出来一个信息：\(f_i\)一定单调不降。

考虑这么一个事情：对于一段到i的后缀max相等的段，根据刚才的性质一定是以段尾为j最优，这样子在一样的max的情况下，这种最靠前，最便宜。所以我们可以这样，在单调队列中按照递减顺序放元素。接下来，考虑使用multiset，把等号右边的东西全都存到里面去，其实存的就是\(f_{q[h]} + a_{q[h+1]}\)。删除时就删掉即可。

注意还要转一个东西：\(f_i = f_{L[i]} + a_{q[h]}\)，这里的L[i]指的是从左往右第一个满足\([L[i] + 1, i]\)和合格的位置。这个最优决策点问题比较新颖。

I.[SCOI2009] 生日礼物

这个是弱智题，好像跟DP没啥关系，直接扫一扫就好了。

J.[POI2005] BAN-Bank Notes

这个是比较重要的单调队列优化多重背包板子。
建议参考这篇博客，写的非常细，还是比较难以理解的。

K.宝物筛选

也是单优背包板子。

L.任务安排1

这个题是这样的，首先设\(f_i\)为前i个物品安排所需的最小费用，发现难以转移，是因为不知道前头分了几个段，有几个S。考虑把时间拆分开来提前向后计算贡献，就是每次要加上后面所有任务的\(c_i\)乘上S。这个提前计算贡献的思路很巧妙。
方程写一下：\(\large f_i = \min\{f_j + S \times (sumc[n] - sumc[j]) + sumt[i] * (sumc[i] - sumc[j])\}\)。

斜率优化DP

其实就是对于一些式子的处理。
可以直接在任务安排2和3中进行讲解。

M.任务安排2

我们把刚才的式子拆解一下，把常数分离出来并进行整理，最后min里面是:
\(f_j - sumc[j] * (S + sumt[i])\)，观察一下，非常像是一次函数的形式。
进行换元:
\(x(j) = sumc[j]\)
\(y(j) = f_j\)
\(k = S + sumt[i]\)
所以这就是一个拿直线去截一个下凸包的截距最小化问题，并且这个斜率单调递增，如图：

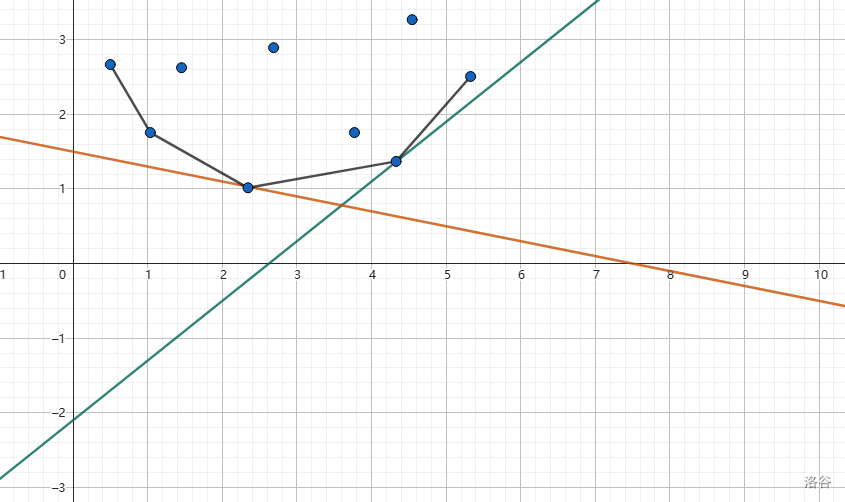
观察一下，只要使用一个单调队列来维护这个下凸包（即斜率单增），每次先弹掉队头所有斜率小于等于直线斜率的点，计算出来\(f_i\)，再把所有加入了i之后斜率不合格的队尾弹出即可。

N.任务安排3

容易发现，本题唯一的区别是斜率不再具有单调性，因此不能每次将队首弹出。使用一个单调栈和二分来找到最优的点，不弹队头即可。

O.[APIO2010] 特别行动队

没什么好说的，直接推就行。

P.[ZJOI2007] 仓库建设

这个题的x好像是递减的，所以需要注意一下斜率的计算方法。然后注意一下，要取最右边有货物的位置的答案，而不是n。

Q.[HNOI2008] 玩具装箱

这个是板子题，就不写了。

R.[Usaco2008 Mar]土地购买

这个题需要着重说一下。
首先发现对于任意\(i,j\)且\(l_j \le l_i, w_j \le w_i\)，事实上j是没有意义的，应当直接去除。然后考虑可以直接升序排序，这样选中的一定是连续段，这一段中\(w\)单增，\(l\)单减，直接选取两头即可。最后斜率优化搞定。
这个题的贪心思想还是很有用的。