背包问题入门(单调队列优化多重背包
背包问题
写这篇文章主要是为了帮帮新人吧,dalao勿喷.qwq
一般的背包问题问法
每种物品都有一个价值w和体积c.//这个就是下面的变量名,请看清再往下看.
你现在有一个背包容积为V,你想用一些物品装背包使得物品总价值最大.
01背包
多种物品,每种物品只有一个.求能获得的最大总价值.
我们考虑是否选择第i件物品时,是需要考虑前i-1件物品对答案的贡献的.
分析
如果我们不选择第i件物品,那我们就相当于是用i-1件物品,填充了体积为v的背包所得到的最优解.
而我们选择第i件物品的时候,我们要得到体积为v的背包,我们需要通过填充用i-1件物品填充得到的体积为v-c[i]的背包得到体积为v的背包.
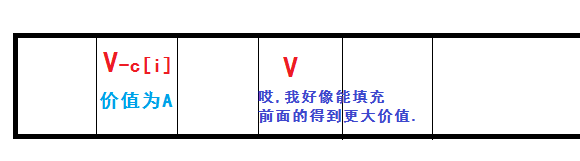
//请保证理解了上面加粗的字再往下看.
所以根据上面的分析,我们很容易设出01背包的二维状态
\(f[i][v]\)代表用i件物品填充为体积为v的背包得到的最大价值.
从而很容易的写出状态转移方程
\(f[i][v]=max(f[i-1][v],f[i-1][v-c[i]]+w[i])\)
状态转移方程是如何得来的?
对于当前第\(i\)件物品,我们需要考虑其是否能让我们得到更优解.
显然,根据上面的话
我们选择第i件物品的时候,我们要得到体积为v的背包,我们需要通过填充用i-1件物品填充得到的体积为v-c[i]的背包得到体积为v的背包.
我们需要考虑到\(v-c[i]\)的情况.
当不选当前第\(i\)件物品的时候,就对应了状态转移方程中的\(f[i-1][v]\),
而选择的时候就对应了\(f[i-1][v-c[i]]+w[i]\).
Q:是不是在状态转移方程中一定会选择当前i物品?
A:不会
我们考虑一个问题.
如果一个体积为5的物品价值为10,而还有一个体积为3的物品价值为12,一个体积为2的物品价值为8.显然我们会选择后者.
这样我们的状态转移方程中就不一定会选择i物品。
其实最好地去理解背包问题的话,还是手跑一下这个过程,会加深理解。
代码写法↓
for(int i=1;i<=n;i++)//枚举 物品
for(int j=1;j<=V;j++)//枚举体积
if(j>=c[i])
f[i][j]=max(f[i-1][j],f[i-1][j-c[i]]+w[i]);//状态转移方程.
else f[i][j]=f[i-1][j].
//上面的if语句是判断当前容量的背包能否被较小体积的背包填充得到.
//显然 如果j-c[i]<0我们无法填充
//(谁家背包负的体积啊 (#`O′)
但是二维下的01背包们还是无法满足,怎么办?
考虑一维如何写!
仔细观察会发现,二维状态中,我们的状态每次都会传递给i(就是说我们的前几行会变得没用.)
这就给了我们写一维dp的机会啊
所以我们理所当然地设状态\(f[i]\)代表体积为i的时候所能得到的最大价值.
容易发现的是,我们的\(f[i]\)只会被i以前的状态影响.
如果我们顺序枚举,我们的\(f[i]\)可能被前面的状态影响.
所以我们考虑倒叙枚举,这样我们的\(f[i]\)不会被i以前的状态影响,而我们更新的话也不会影响其他位置的状态.
(可以手绘一下这个过程,应该不是很难理解.)
或者来这里看看(可能图画的有点丑了
代码写法↓
for(int i=1;i<=n;i++)//枚举 物品
for(int j=V;j>=c[i];j--)//枚举体积
f[j]=max(f[j],f[j-c[i]]+w[i]);//状态转移方程.
//应该不是很难理解.
小结
01背包问题是背包问题中最基础,也是最典型的问题.其状态转移方程也是基础,更可以演变成其他背包的问题.
请保证看懂之后再向下看.
例题-->p1048 采药
完全背包
此类背包问题中,我们的每种物品有无限多个,可重复选取.
类似于01背包,我们依旧需要考虑前i-1件物品的影响.
此时我们依旧可以设得二维状态
\(f[i][v]\)代表用i件物品填充为体积为v的背包得到的最大价值
依旧很容易写出状态转移方程
\(f[i][v]=max(f[i-1][v],f[i-1][j-k*c[i]]+k*w[i])\)
//其中k是我们需要枚举的物品件数.而我们最多选取\(\left\lfloor\frac{V}{c[i]}\right\rfloor\)个(这个应该不用解释
code
for(int i=1;i<=n;i++)//枚举物品
for(int k=1;k<=V/c[i];k++)//我们的物品最多只能放件.
for(int j=1;j<=t;j++)
{
if(c[i]*k<=j)
f[i][j]=max(f[i-1][j],f[i-1][j-k*c[i]]+k*w[i]);
else
f[i][j]=f[i-1][j];
//判断条件与01背包相同.
}
同样地,我们去考虑一维状态(鬼才会考虑
依旧设
\(f[i]\)代表体积为i的时候所能得到的最大价值
与01背包不同的是,我们可以重复选取同一件物品.
此时,我们就需要考虑到前面i-1件物品中是否有已经选取过(其实没必要
即,我们当前选取的物品,可能之前已经选取过.我们需要考虑之前物品对答案的贡献.
因此我们需要顺序枚举.
与01背包一维的写法类似.
代码写法↓
code
for(int i=1;i<=n;i++)//枚举物品
for(int j=c[i];j<=V;j++)//枚举体积.注意这里是顺序/
f[j]=max(f[j,f[j-c[i]]]+w[i]);//状态转移.
如果还是不理解,来这里看看.(就是上面那个连接)
小结
完全背包也是类似于01背包,应该也算上是它的一种变形.
比较一般的写法是一维写法,希望大家能掌握.
例题-->p1616 疯狂的采药
多重背包
此类问题与前两种背包问题不同的是,
这里的物品是有个数限制的.
(下面用\(num[i]\)表示物品i的个数.
我们可以枚举物品个数,也可以二进制拆分打包
同样,我们最多可以放\(\left\lfloor\frac{V}{c[i]}\right\rfloor\),但我们的物品数量可能不够这么多.
因此,我们枚举的物品个数是\(min(\left\lfloor\frac{V}{c[i]}\right\rfloor,num[i])\)
(其实没这么麻烦的,直接枚举到\(num[i]\)即可)
多个物品,我们就可以看成为一个大的物品,再去跑01背包即可.
因此这个大物品的价值为\(k\)×\(w[i]\),体积为\(k\)×\(c[i]\)
code
for(int i=1;i<=n;i++)//枚举物品
for(int j=V;j>=0;j--)//枚举体积
for(int k=1;k<=num[i],k++)
//这个枚举到num[i]更省心
if(j-k*c[i]>=0)//判断能否装下.
f[j]=max(f[j],f[j-k*c[i]]+k*w[i]);
其实还可以对每种物品的个物品跑01背包问题,效率特别低
这里也给出代码
code
for(int i=1;i<=n;i++)
for(int k=1;k<=num[i];k++)
for(int j=V;j>=c[i];j--)
f[j]=max(f[j],f[j-c[i]]+w[i]);
但是此类问题,我们的一般解法却是
二进制拆分
二进制拆分的原理
我们可以用 \(1,2,4,8...2^n\) 表示出\(1\) 到 \(2^{n+1}-1\)的所有数.
考虑我们的二进制表示一个数。
根据等比数列求和,我们很容易知道我们得到的数最大就是\(2^{n+1}-1\)
而我们某一个数用二进制来表示的话,每一位上代表的数都是\(2\)的次幂.
就连奇数也可以,例如->\(19\)可以表示为\(10010_{(2)}\)
这个原理的话应该很好理解,如果实在理解不了的话,还是动手试一试,说服自己相信这一原理.
二进制拆分的做法
因为我们的二进制表示法可以表示从\(1\)到\(num[i]\)的所有数,我们对其进行拆分,就得到好多个大物品(这里的大物品代表多个这样的物品打包得到的一个大物品).
(简单来讲,我们可以用一个大物品代表\(1,2,4,8..\)件物品的和。)
而这些大物品又可以根据上面的原理表示出其他不是2的次幂的物品的和.
因此这样的做法是可行的.
我们又得到了多个大物品,所以再去跑01背包即可.
这里只给出拆分部分的代码,相信你可以码出01背包的代码.
code
for(int i=1;i<=n;i++)
{
for(int j=1;j<=num[i];j<<=1)
//二进制每一位枚举.
//注意要从小到大拆分
{
num[i]-=j;//减去拆分出来的
new_c[++tot]=j*c[i];//合成一个大的物品的体积
new_w[tot]=j*w[i];//合成一个大的物品的价值
}
if(num[i])//判断是否会有余下的部分.
//就好像我们某一件物品为13,显然拆成二进制为1,2,4.
//我们余出来的部分为6,所以需要再来一份.
{
new_c[++tot]=num[i]*c[i];
new_w[tot]=num[i]*w[i];
num[i]=0;
}
}
时间复杂度分析
我们拆分一种物品的时间复杂度为\(log(num[i])\).
我们总共会有n种物品,再配上枚举体积的时间复杂度.
因此,二进制拆分做法的时间复杂度为\(O(\sum_{i=1}^nlog(num[i])\)×\(V )\)
单调队列优化
首先回想多重背包最普通的状态转移方程
\(f[i][j]=max(f[i-1][j],f[i-1][j-k*c[i]]+k*w[i])\)
其中\(k \in [1,min(\left\lfloor\frac{V}{c[i]}\right\rfloor,num[i])]\)
下面用 \(lim\)表示\(min(\left\lfloor\frac{V}{c[i]}\right\rfloor,num[i])\)
容易发现的是\(f[i][j-k*c[i]]\)会被\(f[i][j-(k+1)*c[i]]\)影响 (很明显吧
(我们通过一件体积为\(c[i]\)的物品填充体积为\(j-(k+1)*c[i]\)的背包,会得到体积为\(j-k*c[i]\)的背包.)
归纳来看的话
\(f[i][j]\)将会影响 \(f[i][j+k*c[i]]\) \((j+k*c[i]<=V)\)
栗子
\(c[i]=4\)

容易发现的是,同一颜色的格子,对\(c[i]\)取模得到的余数相同.
且,它们的差满足等差数列! (公差为\(c[i]\).
通项公式为 \(j=k*c[i]+\)取模得到的余数
所以我们可以根据对\(c[i]\)取模得到的余数进行分组.
即可分为\(0,1,2,3{\dots}c[i]-1\) 共\(c[i]\)组
且每组之间的状态转移不互相影响.(注意这里是组.相同颜色为一组
相同颜色的格子,位置靠后的格子,将受到位置靠前格子的影响.
//但是这样的话,我们的格子会重复受到影响.(这里不打算深入讨论 害怕误人子弟
即\(f[9]\)可能受到\(f[5]\)的影响,也可能受到\(f[1]\)的影响
而\(f[5]\)也可能受到\(f[1]\)的影响.
所以我们考虑将原始状态转移方程变形.
重点
这里一些推导过程我会写的尽量详细(我也知道看不懂有多难受. qwq
令d=c[i],a=j/c[i],b=j%c[i]
其中a为全选状况下的物品个数.
则\(j=a*d+b\)
则带入原始的状态转移方程中
\(j-k*d = a*d+b-k*d\) $= (a-k)*d+b $
我们令\((a-k)=k^{'}\)
再回想我们最原始的状态转移方程中第二状态 : \(f[i][j-k*c[i]]+k*w[i]\) 代表选择\(k\)个当前\(i\)物品.
根据单步容斥 :全选\(-\)不选=选.
因此 \(a-(a-k)=k\)
而前面我们已经令\((a-k)=k^{'}\)
而我们要求的状态也就变成了
\(f[i][j]=max(f[i-1][k^{'}*d+b]+a*w[i]-k^{'}*w[i])\)
而其中,我们的\(a*w[i]\)为一个常量(因为a已知.)
所以我们的要求的状态就变成了
\(f[i][j]=max(f[i-1][k^{'}*d+b]-k^{'}*w[i])+a*w[i]\)
根据我们的
\(k \in [1,lim]\)
容易推知
\(k^{'} \in [a-k,a]\)
那么
当前的\(f[i][j]\)求解的就是为\(lim+1\)个数对应的\(f[i-1][k^{'}*d+b]-k^{'}*w[i]\)的最大值.
(之所以为\(lim+1\)个数,是包括当前这个\(j\),还有前面的物品数量.)
将\(f[i][j]\)前面所有的\(f[i-1][k^{'}*d+b]-k^{'}*w[i]\)放入一个队列.
那我们的问题就是求这个最长为\(lim+1\)的队列的最大值+\(a*w[i]\).
因此我们考虑到了单调队列优化( ? ?ω?? )?
(这里不再对单调队列多说.这个题的题解中,有不少讲解此类算法的,如果不会的话还是去看看再来看代码.-->p1886 滑动窗口
//相信你只要仔细看了上面的推导过程,理解下面的代码应该不是很难.
//可能不久的将来我会放一个加注释的代码(不是立flag.
//里面两个while应该是单调队列的一般套路.
//这里枚举的\(k\)就是\(k^{'}\).
code
for(int i=1;i<=n;i++)//枚举物品种类
{
cin>>c[i]>>w[i]>>num[i];//c,w,num分别对应 体积,价值,个数
if(V/c[i] <num[i]) num[i]=V/c[i];//求lim
for(int mo=0;mo<c[i];mo++)//枚举余数
{
head=tail=0;//队列初始化
for(int k=0;k<=(V-mo)/c[i];k++)
{
int x=k;
int y=f[k*c[i]+mo]-k*w[i];
while(head<tail && que[head].pos<k-num)head++;//限制长度
while(head<tail && que[tail-1].value<=y)tail--;
que[tail].value=y,que[tail].pos=x;
tail++;
f[k*c[i]+mo]=que[head].value+k*w[i];
//加上k*w[i]的原因:
//我们的单调队列维护的是前i-1种的状态最大值.
//因此这里加上k*w[i].
}
}
}
时间复杂度分析
这里只简单的进行一下分析.(其实我也不大会分析 qwq
我们做一次单调队列的时间复杂度为\(O(n)\)
而对应的每次枚举体积为\(O(V)\)
因此总的时间复杂度为\(O(n*V)\)
小结
多重背包的写法一般为二进制拆分.
单调队列写法有些超出noip范围,但时间复杂度更优,能掌握还是尽量去掌握.
拆分物品这种思想应该不算很难理解,这个是比较一般的写法.希望大家能掌握.
如果还是比较抽象,希望大家能动笔尝试一下.
例题-->p1776 宝物筛选(这个题之前还是个pj/tg-,后来竟然蓝了 emmm
混合三种背包
所谓的混合三种背包就是存在三种物品。
一种物品有无数个(完全背包),一种物品有1个(01背包),一种物品有\(num[i]\)个(多重背包)
这个时候一般只需要判断是哪一种背包即可,再对应地去选择dp方程求解即可.
送上一波伪代码
code
for(int i=1;i<=n;i++)
{
if(完全背包)
{
for(int j=c[i];j<=V;j++)
f[j]=max(f[j],f[j-c[i]]+w[i]);
}
else if(01背包)
{
for(int j=V;j>=c[i];j--)
f[j]=max(f[j],f[j-c[i]]+w[i]);
}
else//否则就是完全背包了
{
for(int j=V;j>=0;j--)
for(int k=1;k<=num[i];k++)
if(j-k*c[i]>=0)
f[j]=max(f[j],f[j-k*c[i]]+k*w[i]);
}
}
//完全背包拆分的话,可以当做01背包来做.(提供思路
小结
混合三种背包问题应该不是很难理解(如果前面三种背包你真正了解了的话.
结合起来考的话应该也不会很多.
(毕竟背包问题太水了
例题:(这个我真的没找到qwq
分组背包
一般分组背包问题中,每组中只能选择一件物品.
状态大家都会设\(f[k][v]\)代表前k组物品构成体积为v的背包所能取得的最大价值和.
状态转移方程也很容易想.
\(f[k][v]=max(f[k-1][v],f[k-1][v-c[i]]+w[i])\)
但是我们每组物品中只能选择一件物品.
//这个时候我们就需要用到01背包倒叙枚举的思想.
code:
for(int i=1;i<=k;i++)//枚举组别
for(int j=V;j>=0;j--)//枚举体积
for(now=belong[i])//枚举第i组的物品.
{
if(j-c[i]>=0)
f[i][j]=max(f[i-1][j],f[i-1][j-c[now]]+w[now]);
else
f[i][j]=f[i-1][j];
}
小结
这类问题是01背包的演变,需要注意的位置就是我们枚举体积要在枚举第i组的物品之前
(因为每组只能选一个!)
有依赖的背包
此类背包问题中。如果我们想选择物品i的附件,那我们必须选择物品i.
在[Noip2006]金明的预算方案这题中.引入了主件与附件的关系.
就好比你买电扇必须先买电.
一个主件和它的附件集合实际上对应于分组背包中的一个物品组.
每个选择了主件又选择了若干附件的策略,对应这个物品组的中的一个物品.
(也就是说,我们把'一个主件和它的附件集合'看成为了一个能获得的最大价值的物品.)
具体实现呢?
我们的主件有一些附件伴随,我们可以选择购买附件,也可以不购买附件.
(当然我们也可以选择不购买主件.
当我们选择一个主件的时候,我们希望得到的肯定是最大价值.
如何做?
我们可以先对附件集合跑一遍01背包,从而获得这一主件及其附件集合的最大的价值.
(或者是完全背包,视情况而定.)
代码大致写法是这样的↓
(每个物品体积为1,\(w[]\)代表价值.)
不敢保证正确性,不过一般都是这样写的qwq
for(int i=1;i<=n;i++)//枚举主件.
{
memset(g,0,sizeof g);//做01背包要初始化.
for(now=belong[i])//枚举第i件物品的附件.
{
for(int j=V-1;j>=c[now];j--)//因为要先选择主件才能选择附件,所以我们从V-1开始.
{
g[j]=max(g[j],g[j-1]+w[now]);
}
}
g[V]=g[V-1]+w[i];
for(int j=V;j>=0;j--)
for(int k=1;k<=V;k++)//此时相当于"打包" ..
{
if(j-k>=0)
f[j]=max(f[j],f[j-k]+w[i]+g[k-1]);
}
}
printf("%d",f[V]);
有一种情况,是主件的附件依旧有附件.(不会互相依赖.
对于这种依赖关系,我们可以构出这样的图.
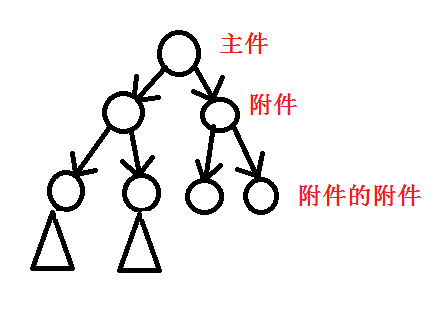
这种背包就是传说中的树形背包.
(树形dp的一种)(应该后面会有人讲)或者等我讲
这题就是一个典型的树形背包入门题
小结
这类问题更是背包问题的延伸,我们需要考虑的就是如何取到每一个主件及其附件的集合中的最大值.而这就运用到了前面01背包.
例题-->p1064 金明的预算方案
泛化物品
前面两种背包问题,已经有了泛化物品的影子.
(哪里有啊!喂,话说这是什么鬼东西
先给出概念.
该类物品并没有固定的体积和价值,而是它的价值随着你分配给它的体积而变化
其实这个可以抽象成一个函数图象.
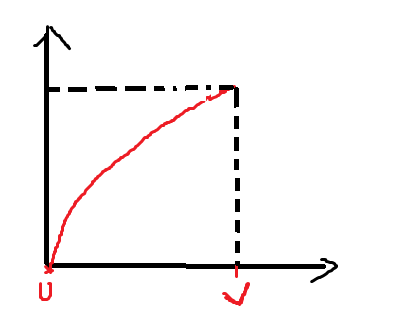
在定义域0~V中,此类物品的价值随着分配给它的价值变化而变化.
(可能不是一次函数也不是二次函数.
毕竟我没有遇到过这种题
现在应该很容易理解.
有依赖的背包问题就有着这种泛化物品的思想.
如果对于某一个物品组,我们分配给它的体积越大,显然它的价值越大.
最终我们的答案就是所有对答案有贡献的物品组的和.(保证在限制范围内.
这些物品组被分配体积的大小的限制就是0~V.
总的限制也是0~V,所以这就可以抽象为
最终结果\(f(V)=max(h(l)+g(V-l))\)
(这只是一个抽象的解释,还需要具体问题具体分析.
背包问题的变化.
随着水平的提高(反正窝很弱QAQ
出题人会更加考察选手的思维.(话说有这种毒瘤出题人嘛qwq
下面讨论几种变化.根据背包九讲的顺序.
输出方案
对于一个背包问题,我们已经得到了最大价值.
现在良心毒瘤出题人要求你输出选择物品的方案
分析
我们现在需要考虑的是如何记录这个状态.
很明显记录每个状态的最优值,是由状态转移方程的哪一项推出来的.
如果我们知道了当前状态是由哪一个状态推出来的,那我们很容易的就能输出方案.
开数组\(g[i][v]\)记录状态\(f[i][v]\)是由状态转移方程哪一项推出.
//以01背包一维写法为例.
code
for(int i=1;i<=n;i++)
{
for(int j=V;j>=c[i];j--)
{
if(f[j]<f[j-c[i]]+w[i])
{
f[j]=f[j-c[i]]+w[i];
g[i][j]=true;///选第i件物品
}
else g[i][j]=false;///不选第i件物品
}
}
输出
code
int T=V;
for(int i=n;i>=1;i--)
{
if(g[i][T])
{
printf("used %d",i);
T-=c[i];//减去物品i的体积.
}
}
不敢保证正确性,不过一般都是这样写的qwq
再放一下状态转移方程.
\(f[i][v]=max(f[i-1][v],f[i-1][v-c[i]]+w[i]\)
\(f[j]=max(f[j],f[j-c[i]]+w[i])\)
二维状态可以省去g数组,只需要判断\(f[i][v]\)是等于\(f[i-1][v]\)还是等于\(f[i-1][v-c[i]]+w[i]\)就能输出方案.
一维状态好像不能,我不会啊qwq
输出字典序较小的最优方案
感觉sort一下就可以吧
根据原文叙述来看,是将物品逆序排列一下.
与上面输出方案的解法相同(倒叙枚举.
唯一需要判断的是:
当\(f[i][v]==f[i-1][v]\) 并且\(f[i][v]==f[i-1][v-c[i]]+w[i]\)的时候.
我们要选择后面这个方案.因为这样选择的话,我们会得到更小的字典序.(很明显吧
** 求次优解or第k优解 **
此类问题应该是比较难理解.
所以我会尽量去详细地解释,qwq.
前置知识
首先根据01背包的递推式:(这里按照一维数组来讲)
(v[i]代表物品i的体积,w[i]代表物品i的价值).
\(f(j)\)=\(max\left(f(j),f(j-v[i])+w[i]\right)\)
很容易发现\(f(j)\)的大小只会与\(f(j)\)、\(f(j-v[i])+w[i]\)有关
我们设\(f[i][k]\)代表体积为i的时候,第k优解的值.
则从\(f[i][1]\)...\(f[i][k]\)一定是一个单调的序列.
\(f[i][1]\)即代表体积为i的时候的最优解
解析
很容易发现,我们需要知道的是,能否通过使用某一物品填充其他体积的背包得到当前体积下的更优解.
我们用体积为7价值为10的物品填充成体积为7的背包,得到的价值为10.
而我们发现又可以通过一件体积为3价值为12的物品填充一个体积为4价值为6的背包得到价值为18.
此时我们体积为7的背包能取得的最优解为18,次优解为10.
我们发现,这个体积为4的背包还有次优解4(它可能被两个体积为2的物品填充.)
此时我们可以通过这个次优解继续更新体积为7的背包.
最终结果为 18 16 10
因此我们需要记录一个变量c1表示体积为j的时候的第c1优解能否被更新.
再去记录一个变量c2表示体积为j-v[i]的时候的第c2优解.
简单概括一下
我们可以用v[i]去填充j-v[i]的背包去得到体积为j的情况,并获得价值w[i].
同理j-v[i]也可以被其他物品填充而获得价值.
此时,如果我们使用的填充物不同,我们得到的价值就不同.
这是一个刷表的过程(或者叫推表?
为什么是正确的?
(这里引用一句话)
一个正确的状态转移方程的求解过程遍历了所有可用的策略,也就覆盖了问题的所有方案。
做法
考虑到我们的最优解可能变化,变化成次优解.只用一个二维数组\(f[i][k]\)来实现可能会很困难.
所以我们引入了一个新数组\(now[]\)来记录当前状态的第几优解.
\(now[k]\)即代表当前体积为i的时候的第k优解.
因此最后我们可以直接将\(now[]\)的值赋给\(f[i]\)数组
具体实现的话可以看看我的这篇文章
例题的话也就是这个(上面的文章是这题的题解.里面有详细解释.
主要参考-->dd大牛的《背包九讲》
强大的合伙人-->w_x_c_q
如果还是有不懂的地方,希望可以多多提问.
(毕竟我也不是个坏人,qwq)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号