【学习笔记】斜率优化 DP

斜率优化 DP

斜率优化，主要是针对类似于 \(f_i=\min/\max_{j=0}^{i-1}\{f_j+A(j)+B(i)+C(i) \times D(j)\}\) 的情况的优化。（注：若是没有 \(C(i) \times D(j)\) 则可以用单调队列来优化。 ）

我们有两种方式来解决这类题目。

方法一：

理解：

我们可以通过移项，将其转化成类似于 \(y=kx+b\) ，即 \(f_j+A(i)=-C(i) \times D(j)+f_i-B(i)\) 的形式。

对于 \(j\) 来说，可以将其看成坐标的形式，即 \((D(j),f_j+A(j))\) 。

而对于 \(i\) 我们将其看为 \(y=kx+b\) 的形式。其中：

\(k=-C(i)\)

\(b=f_i-B(i)\)

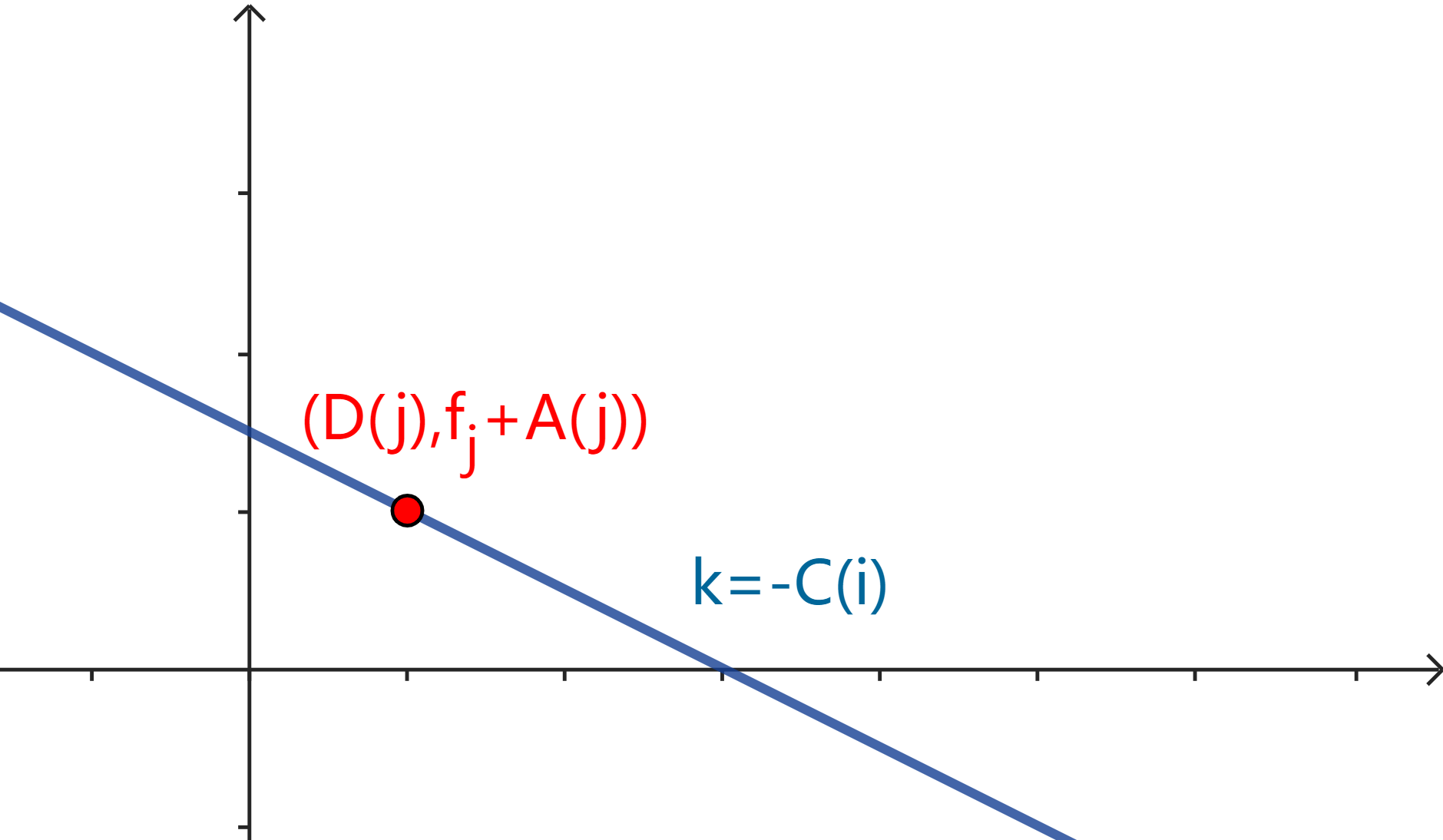
因为 \(B(i)\) 是定值，所以对于一个 \(i\)，我们需要找出一个 \(j\) \((1 \le j < i)\)，满足 \(b\) 最小（或最大）。

若 \(D(j)\) 单调递增，\(-C(i)\) 单调递减，则可以用单调队列维护一个下凸包（如图），即满足斜率 \(k\) 递增。（ \(\max\) 相反）

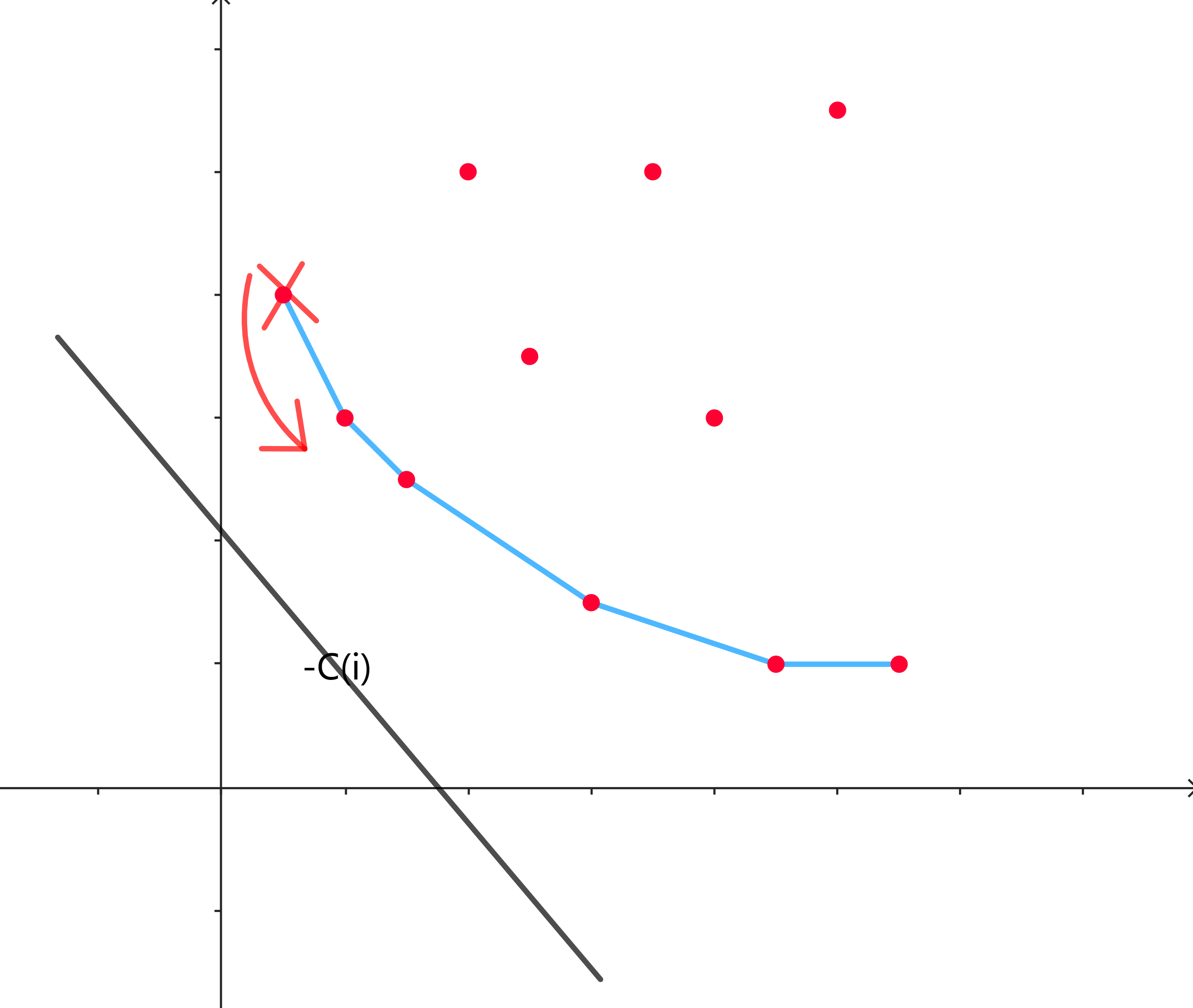
大概来讲就是有一条直线的斜率为 \(-C(i)\) 的直线，通过平移遇到的第一个点所得到的 \(b\) 即为答案。

如何处理单调队列：

1. 进行择优筛选时，在凸包上找到最优决策点 \(j\) 。
2. 用最优决策点 \(j\) 更新 \(f_i\) 。
3. 将 \(i\) 作为一个决策点加入图形并更新凸包（如果点 \(i\) 也是 \(f_i\) 的决策点之一，则需要将步骤3换到最前面）。

Code

以 P3195 [HNOI2008] 玩具装箱 - 洛谷 为例：

本题处理中步骤一的择优筛选中，将所有 \(k\) 大于队首两点斜率的队首的点弹出，可以写成这样：

while(l<r && slope(q[l],q[l+1])<=-C(i)) l++;

此时需满足队列里有两个及以上个点。

步骤三中，插入一个点 \(i\) 时，将其与队尾的两个点进行比较（如图）

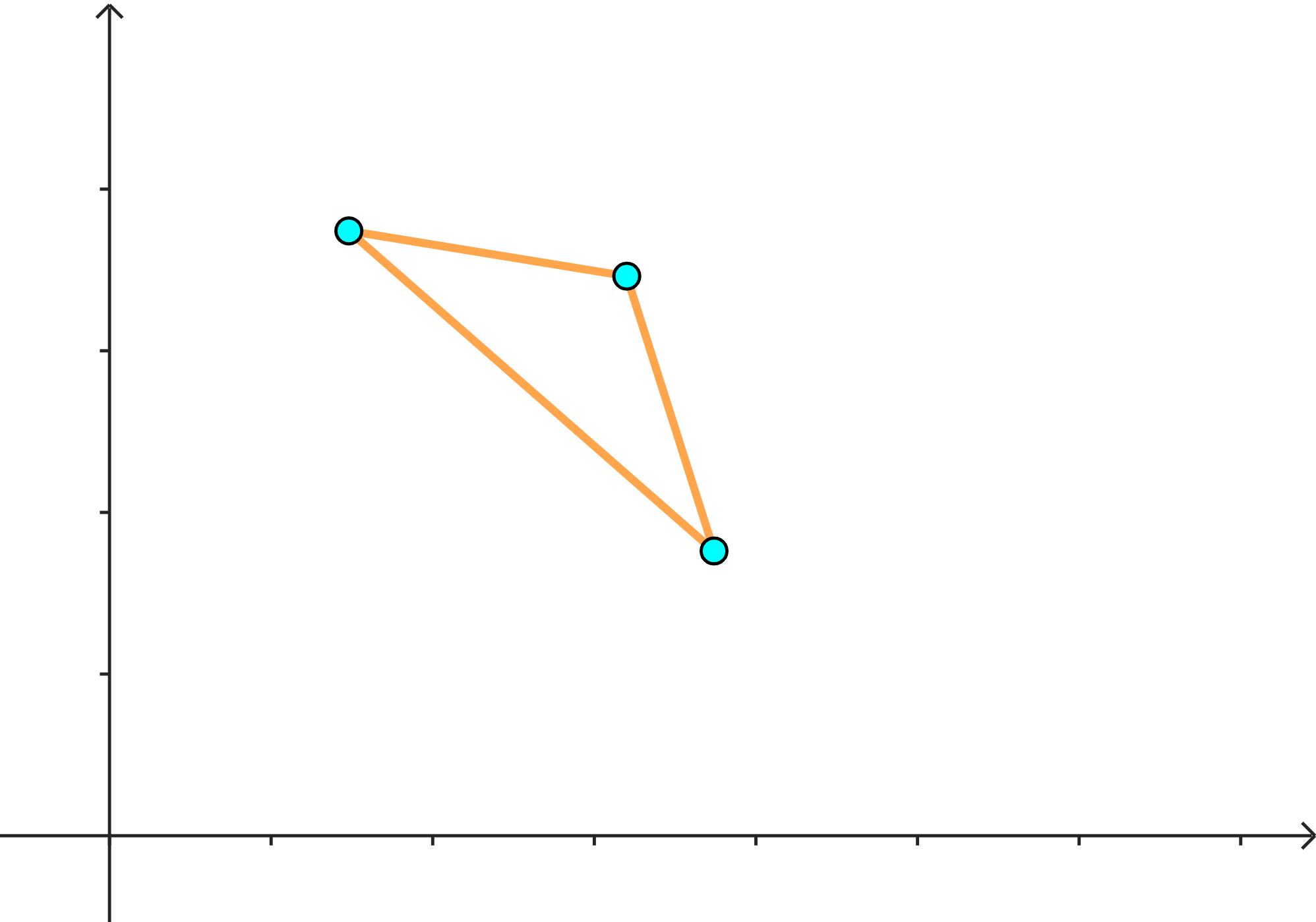
大概看一下，此时中间这个点是无效的，需弹出，可以写成这样：

while(l<r && slope(q[r-1],q[r])>=slope(i,q[r-1])) r--;

代码如下：

#include<bits/stdc++.h>
#define IOS cin.tie(0),cout.tie(0),ios::sync_with_stdio(0)
#define mod 998244353
#define ll long long
#define db double
#define ldb long double
using namespace std;
const int N=1e5+5;
namespace DP{
	ll L,s[N],f[N];
	ll A(int j){return s[j]*s[j]+2*s[j]*L+2*s[j];}
	ll B(int i){return s[i]*s[i]-2*s[i]*L-2*s[i];}
	ll C(int i){return -2*s[i];}
	ll D(int j){return s[j];}
	ll X(int o){return D(o);}
	ll Y(int o){return f[o]+A(o);}
	ldb slope(int i,int j){
		return (ldb)(Y(j)-Y(i))/(ldb)(X(j)-X(i));
	}
}
using namespace DP;
int n,c[N],q[N];
void Debug(auto *oo,int l,int r){
	for(int i=l;i<=r;i++) cout<<oo[i]<<" ";cout<<"\n\n";
}
int main(){
	IOS;cin>>n>>L;
	for(int i=1;i<=n;i++){
		cin>>c[i];
		s[i]=s[i-1]+c[i]+1;
	}
	int l=1,r=0;
	q[++r]=0;
	for(int i=1;i<=n;i++){
		while(l<r && slope(q[l],q[l+1])<=-C(i)) l++;
		int j=q[l];
		f[i]=f[j]+A(j)+B(i)+C(i)*D(j)+(L+1)*(L+1);
		while(l<r && slope(q[r-1],q[r])>=slope(i,q[r-1])) r--;
		q[++r]=i;
//		cout<<i<<" ";if(l<=r) Debug(q,l,r);
	}
	cout<<f[n];
	return 0;
}

方法二：

理解

通过移项将原式化为 \(f_i-B(i)=f_j+A(j)+C(i) \times D(j)\)。

类似于方法一，我们将其看作一次函数 \(y=kx+b\)。其中：

\(y=f_i-B(i)\)

\(k=D(j)\)

\(b=f_j+A(j)\)

相当于对于一个 \(i\)，求 \(i=C(i) , y_{\max}\)。此时我们需维护一个凸包。（如图，红色为维护的一个凸包。）

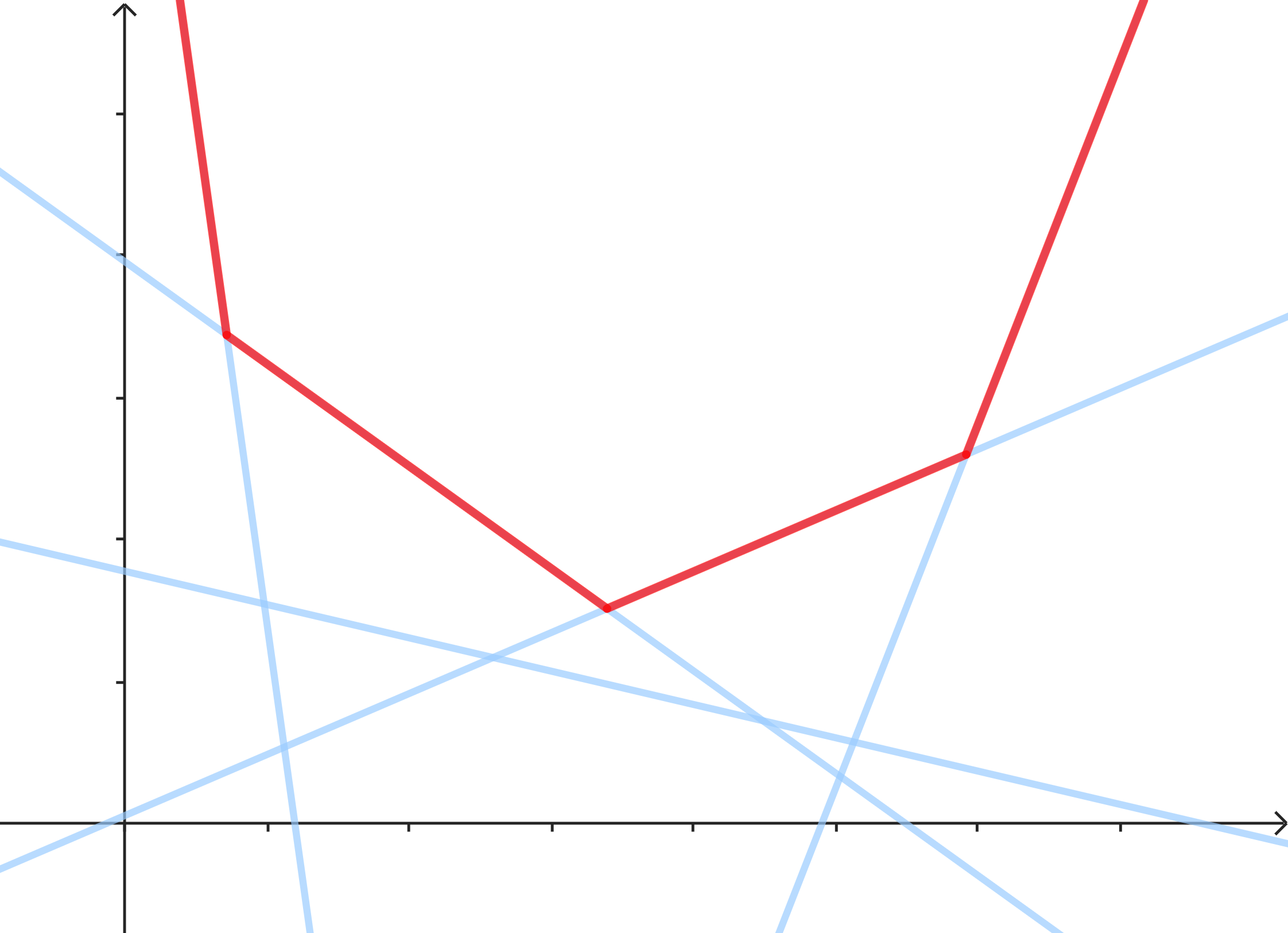
支持两个操作：

1. 插入直线
2. 查询 \(x=C(i),y_{\max}\)。

若满足 \(C(i),D(j)\) 单调递增，则可用单调队列维护。（具体见方法一）

若不满足，则需要用到一个数据结构：李超线段树。

复杂度 \(O(n \log n)\)。

Code

以 P5785 [SDOI2012] 任务安排 - 洛谷 为例：

#include<bits/stdc++.h>
#define IOS cin.tie(0),cout.tie(0),ios::sync_with_stdio(0)
#define ll long long
#define pdi pair<int,int>
using namespace std;
const int N=3e5+5;
const ll INF=(long double)(1e18+7);
namespace LCT{//李超线段树
	int cnt,s[N<<2],Ln;
	vector<ll> tc;
	struct lne{
		ll k,b;
		#define k(p) le[p].k
		#define b(p) le[p].b
	}le[N];
	ll calc(int id,int xx){
		xx=tc[xx];
		return k(id)*xx+b(id);
	}
	void update(int p,int l,int r,int u){
		int &v=s[p],mid=(l+r)>>1;
		if(v==0){v=u;} 
		if(calc(u,mid)<calc(v,mid)) swap(v,u);
		if(calc(u,l)<calc(v,l)) update(p<<1,l,mid,u);
		if(calc(u,r)<calc(v,r)) update(p<<1|1,mid+1,r,u);
		return ;
	}
	ll query(int p,int l,int r,int d){
		if(r<d || d<l) return INF;
		ll res=calc(s[p],d);
		if(l==r) return res;
		int mid=(l+r)>>1;
		return min({res,query(p<<1,l,mid,d),query(p<<1|1,mid+1,r,d)});
	}
	void change(ll k,ll b){
		k(++cnt)=k;
		b(cnt)=b;
		update(1,1,Ln,cnt);	
	}
}
namespace DP{
	ll L,t[N],c[N];
	ll A(int j){return -L*c[j];}
	ll B(int i){return t[i]*c[i];}
	ll C(int i){return t[i];}
	ll D(int j){return -c[j];}
}
using namespace DP;
using namespace LCT;
int n;
ll f[N];
int main(){
	cin>>n>>L;
	for(int i=1;i<=n;i++){
		cin>>t[i]>>c[i];
		t[i]+=t[i-1];
		c[i]+=c[i-1];
		tc.push_back(t[i]);
	}
	sort(tc.begin(),tc.end());
	tc.erase(unique(tc.begin(),tc.end()),tc.end());
	Ln=tc.size()-1;
	f[1]=t[1]*c[1]+L*c[n];
	change(D(1),f[1]+A(1));
	for(int i=2;i<=n;i++){
		int d=lower_bound(tc.begin(),tc.end(),C(i))-tc.begin();
		f[i]=t[i]*c[i]+L*c[n];
		f[i]=min(f[i],query(1,1,Ln,d)+B(i)+L*c[n]);
		change(D(i),f[i]+A(i));
	}
	cout<<f[n]<<"\n";
	return 0;
}