BoydC5pt2

---

Previous part: BoydC5pt1

---

Geometric interpretation

Weak and strong duality via set of values

interpretation of dual function:

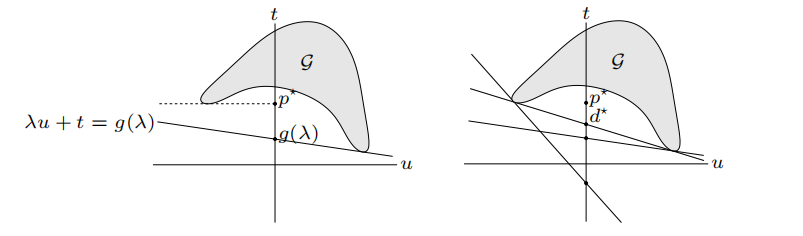
\(t=-\lambda u+g(\lambda)\) is (non-vertical) supporting hyperplane to \(\mathcal{G}\) and \(d^* = \sup_{\lambda}g(\lambda)\leq p^*\).

epigraph variation: same interpretation if \(\mathcal{G}\) is replaced with

\[\mathcal{A} = \left\{ (u,t) \mid f_1(x) \leq u, f_0(x) \leq t \text{ for some } x \in \mathcal{D} \right\} \]

\(\mathcal{A}\) includes all the points in \(\mathcal{G}\), as well as points that are 'worse', \(i.e.\), those with larger objective or inequality constraint function values. \(p^* = \inf\{t~|~(0,t)\in\mathcal{A}\}\)

strong duality

• holds if there is a non-vertical supporting hyperplane to \(\mathcal{A}\) at \((0,p^*)\)
• for convex problem, \(\mathcal{A}\) is convex, hence has supp. hyperplane at \((0,p^*)\)
• Slater’s condition: if there exist \((\tilde{u},\tilde{t})\in\mathcal{A}\) with \(\tilde{u}<0\), then supporting hyperplanes at \((0,p^*)\) must be non-vertical (and \(\lambda\succeq 0\))

---

Next part: BoydC5pt3