P3369 【模板】普通平衡树

P3369 【模板】普通平衡树

大意

  1. 插入
  2. 删除
  3. 查询排名
  4. 查询排名值
  5. 查询前驱
  6. 查询后继

思路

采用 Splay 和 Treap 两种方式。

Treap

首先 Treap 是一种随机化算法，我们采用 二叉搜索树 + 随机化 的方式实现，具体的来说：

首先我们给每个点都随机赋上一个点权，然后使得这棵树在满足 BST 得到基础上再去满足这个堆的性质。

复杂度证明：

设 \(D(v)\) 为节点 \(v\) 的深度。引入指示变量 \(I(u, v)\)：

\[I(u, v) = \begin{cases} 1, & u \text{ 是 } v \text{ 的祖先} \\ 0, & \text{其他} \end{cases} \]

根据期望的线性性，节点 \(v\) 的深度期望值为：

\[E[D(v)] = \sum_{u=1}^n E[I(u, v)] = \sum_{u=1}^n P(u \text{ 是 } v \text{ 的祖先}) \]

在 Treap 中，\(u\) 是 \(v\) 的祖先，当且仅当在数值区间 \([\min(u, v), \max(u, v)]\) 之间的所有节点中，\(u\) 的随机权值 \(w(u)\) 是最大的。

  • 区间内的节点个数为：\(k = |u - v| + 1\)。

由于所有节点的随机权值 \(w(i)\) 独立同分布，区间内任何一个节点成为最大值的概率是相等的。因此：

\[P(u \text{ 是 } v \text{ 的祖先}) = \frac{1}{|u - v| + 1} \]

对所有可能的 \(u\) 进行求和：

\[\begin{aligned} E[D(v)] &= \sum_{u=1}^n \frac{1}{|u - v| + 1} \\ &= \sum_{i=1}^{v-1} \frac{1}{v-i+1} + 1 + \sum_{i=v+1}^n \frac{1}{i-v+1} \\ &< \sum_{k=1}^n \frac{1}{k} + \sum_{k=1}^n \frac{1}{k} \end{aligned} \]

利用调和级数近似公式 \(\sum_{k=1}^n \frac{1}{k} = \ln n + O(1)\)：

\[E[D(v)] < 2H_n = O(\log n) \]

结论： Treap 的平均深度随节点数 \(n\) 呈对数级增长。

Splay

我们考虑将每次查询的点或者插入的点都旋转到根，这样可以不让树退化。

但是如果是单旋的话会出现这样的问题

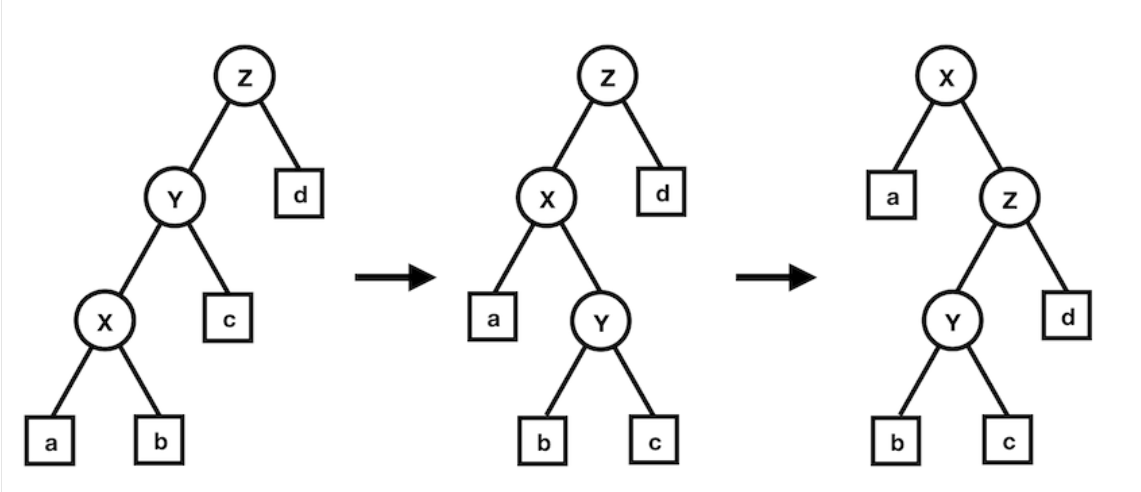
image

我们发现这个玩意压根就没有发生变化，这也就是说，这玩意有可能退化（太可怕了）

那么我们采用双旋的方式去解决这个问题，类似这样：

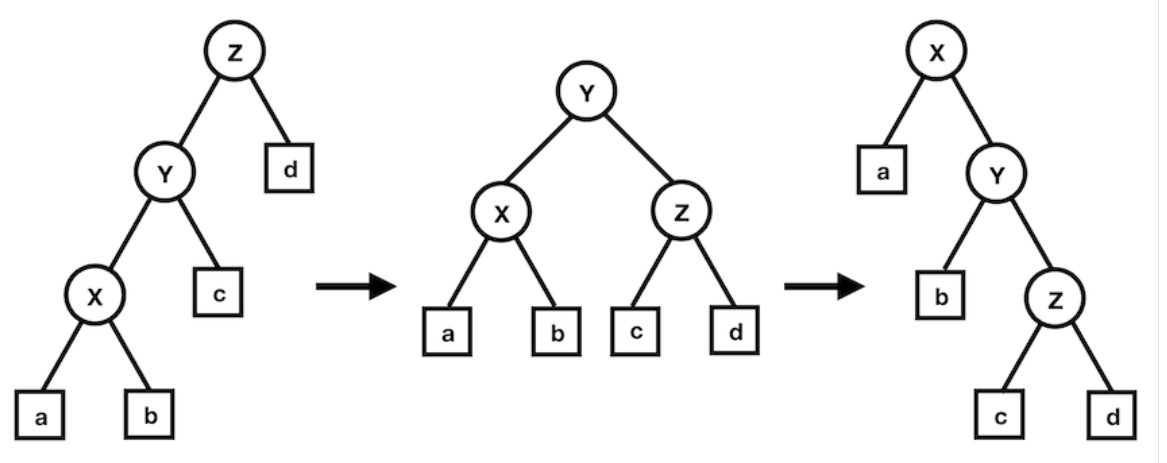
image

我们先把 \(x\) 的父亲更改，再处理 \(x\) 的儿子与 \(y\) 处理，最后让 \(y\) 成为 \(x\) 的儿子。

这样我们就做出了 rotate 函数，在旋转的时候，分为同侧旋转与异侧旋转，如果是同侧的话就旋转 \(y\) 再旋 \(x\)，如果是异侧就双次旋转 \(x\)。

复杂度证明：

不会。
参考大佬的证明

代码

//Treap

#include <iostream>
#include <ctime>
#include <cstdlib>
using namespace std;

#define lc(x) t[x].s[0]
#define rc(x) t[x].s[1]

const int MAXN = 1e5 + 5;
const int INF = (1 << 30) - 1;

struct node{
	int s[2], v, p, cnt, sz;
	void init(int val){
		v = val, p = rand();
		cnt = sz = 1;
		s[0] = s[1] = 0;
	}
}t[MAXN];

int root, tot = 0;

void pushup(int x){
	t[x].sz = t[lc(x)].sz + t[rc(x)].sz + t[x].cnt;
}

void rotate(int &x, int d){
	int y = t[x].s[d];
	t[x].s[d] = t[y].s[d ^ 1];
	t[y].s[d ^ 1] = x;

	pushup(x);
	pushup(y);
	x = y;
}

void Insert(int &x, int val){
	if(!x){
		x = ++ tot;
		t[x].init(val);
		return;
	}

	if(t[x].v == val) t[x].cnt ++;
	else{
		int d = val > t[x].v;
		Insert(t[x].s[d], val);
		if(t[t[x].s[d]].p > t[x].p) rotate(x, d);
	}

	pushup(x);
}

void Delete(int &x, int val){
	if(!x) return;

	if(t[x].v == val){
		if(t[x].cnt > 1) t[x].cnt --;
		else{
			if(!lc(x) || !rc(x)) x = lc(x) + rc(x);
			else{
				int d = t[rc(x)].p > t[lc(x)].p;
				rotate(x, d);
				Delete(t[x].s[d ^ 1], val);
			}
		}
	}
	else Delete(t[x].s[val > t[x].v], val);

	if(x) pushup(x);
}

int Rank(int x, int val){
	if(!x) return 1;
	if(t[x].v == val) return t[lc(x)].sz + 1;
	if(val < t[x].v) return Rank(lc(x), val);
	return t[lc(x)].sz + t[x].cnt + Rank(rc(x), val);
}

int Val(int x, int k){
	if(!x) return 0;
	if(k <= t[lc(x)].sz) return Val(lc(x), k);
	else if(k <= t[lc(x)].sz + t[x].cnt) return t[x].v;
	else return Val(rc(x), k - t[lc(x)].sz - t[x].cnt);
}

int Pre(int val){
	int x = root, res = -INF;
	while(x){
		if(t[x].v < val) res = t[x].v, x = rc(x);
		else x = lc(x);
	}
	return res;
}

int Suc(int val){
	int x = root, res = INF;
	while(x){
		if(t[x].v > val) res = t[x].v, x = lc(x);
		else x = rc(x);
	}
	return res;
}

int n, op, x;

int main(){
	srand(time(0));
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> n;
	while(n --){
		cin >> op >> x;
		if(op == 1) Insert(root, x);
		else if(op == 2) Delete(root, x);
		else if(op == 3) cout << Rank(root, x) << '\n';
		else if(op == 4) cout << Val(root, x) << '\n';
		else if(op == 5) cout << Pre(x) << '\n';
		else cout << Suc(x) << '\n';
	}

	return 0;
}

//Splay

#include<iostream>
using namespace std;

#define lc(x) t[x].s[0]
#define rc(x) t[x].s[1]

const int MAXN = 1e5 + 5;
const int INF = (1 << 30) - 1;

struct node{
	int s[2], f, v, cnt, sz;
	void init(int fa, int val){
		f = fa, v = val;
		cnt = sz = 1;
	}
}t[MAXN];

int root, tot = 0;

void pushup(int x){
	t[x].sz = t[lc(x)].sz + t[rc(x)].sz + t[x].cnt;
}

void rotate(int x){
	int y = t[x].f, z = t[y].f;
	int k = (rc(y) == x);
	t[z].s[rc(z) == y] = x;
	t[x].f = z;
	
	t[y].s[k] = t[x].s[k ^ 1];
	t[t[x].s[k ^ 1]].f = y;
	
	t[x].s[k ^ 1] = y;
	t[y].f = x;

	pushup(y);
	pushup(x);
}

void Splay(int x, int k){
	while(t[x].f != k){
		int y = t[x].f, z = t[y].f;
		if(z != k){
			((lc(z) == y) ^ (lc(y) == x)) ? rotate(x) : rotate(y);
		}
		rotate(x);
	}
	if(k == 0) root = x;
}

void Insert(int val){
	int x = root, f = 0;
	while(x && t[x].v != val){
		f = x;
		x = t[x].s[val > t[x].v];
	}
	if(x) t[x].cnt ++;
	else{
		x = ++ tot;
		if(f){
			t[f].s[val > t[f].v] = x;
		}
		t[x].init(f, val);
	}
	Splay(x, 0);
}

void Find(int val){
	int x = root;
	while(t[x].s[val > t[x].v] && t[x].v != val){
		x = t[x].s[val > t[x].v];
	}
	Splay(x, 0);
}

int Pre(int val){
	Find(val);
	int x = root;
	if(t[x].v < val) return x;
	x = lc(x);
	while(rc(x)) x = rc(x);
	Splay(x, 0);
	return x;
}

int Suc(int val){
	Find(val);
	int x = root;
	if(t[x].v > val) return x;
	x = rc(x);
	while(lc(x)) x = lc(x);
	Splay(x, 0);
	return x;
}

void Delete(int val){
	int pre = Pre(val), suc = Suc(val);
	Splay(pre, 0), Splay(suc, pre);
	int x = lc(suc);
	if(t[x].cnt > 1){
		t[x].cnt --;
		Splay(x, 0);
	}
	else{
		lc(suc) = 0;
		Splay(suc, 0);
	}
}

int Rank(int val){
	Insert(val);
	int res = t[lc(root)].sz;
	Delete(val);
	return res;
}

int Val(int k){
	int x = root;
	while(true){
		if(k <= t[lc(x)].sz){
			x = lc(x);
		}
		else if(k <= t[lc(x)].sz + t[x].cnt){
			break;
		}
		else{
			k -= (t[lc(x)].sz + t[x].cnt);
			x = rc(x);
		}
	}
	Splay(x, 0);
	return t[x].v;
}

int n, op, x;

int main(){
	ios::sync_with_stdio(0);
	cin.tie(0);
	cin >> n;
	Insert(-INF), Insert(INF);
	while(n --){
		cin >> op >> x;
		if(op == 1){
			Insert(x);
		}
		else if(op == 2){
			Delete(x);
		}
		else if(op == 3){
			cout << Rank(x) << '\n';
		}
		else if(op == 4){
			cout << Val(x + 1) << '\n';
		}
		else if(op == 5){
			cout << t[Pre(x)].v << '\n';
		}
		else{
			cout << t[Suc(x)].v << '\n';
		}
	}
	return 0;
}
posted @ 2026-01-16 21:33  To_Carpe_Diem  阅读(0)  评论(0)    收藏  举报