「作业」

目录

• 部分自选题（基本口胡）
• A(2014 ACM-ICPC World Finals)
• B(2015 ACM-ICPC World Finals)
• C(2016 ACM-ICPC World Finals)
• D(2017 ACM-ICPC World Finals)
• E(2018 ACM-ICPC World Finals)
• F(2019 ICPC World Finals)
• G(2017-2018 ACM-ICPC Northern Eurasia (Northeastern European Regional) Contest (NEERC 17))
• H(2016-2017 ACM-ICPC Northeastern European Regional Contest (NEERC 16))
• I(2015-2016 ACM-ICPC Northeastern European Regional Contest (NEERC 15))
• J(2014-2015 ACM-ICPC Northeastern European Regional Contest (NEERC 14))
• K(2013-2014 ACM-ICPC Northeastern European Regional Contest (NEERC 13))
• L(2017-2018 ACM-ICPC, Central Europe Regional Contest (CERC 17))
• M(2016-2017 ACM-ICPC, Central Europe Regional Contest (CERC 16))
• N(2015-2016 ACM-ICPC, Central Europe Regional Contest (CERC 15))
• O(2014-2015 ACM-ICPC, Central Europe Regional Contest (CERC 14))
• P(2013-2014 ACM ICPC Central European Regional Contest (CERC 13))
• Q(2017-2018 ACM-ICPC, NEERC, Northern Subregional Contest)
• R(2016-2017 ACM-ICPC, NEERC, Northern Subregional Contest)
• S(2015-2016 ACM-ICPC, NEERC, Northern Subregional Contest)
• T(2014-2015 ACM-ICPC, NEERC, Northern Subregional Contest)
• U(2013-2014 ACM-ICPC, NEERC, Northern Subregional Contest)

---

目前：131/150。

在做了在做了。

2020/10/19：五十道。感觉写了一大车模拟题。

2020/10/28：一百道。跳了一大车计算几何还有大大大模拟。以及 WF 的平均难度和 NEERC/CERC 差得好像有点大。

2020/11/2：由于我太菜了，所以，很抱歉，这份作业咕掉了。

（有 * 标记的并非独立思考出来的，即参考了题解或与国集大佬讨论过后得到的思路）

---

部分自选题（基本口胡）

没写的题会在后面加上 “(?)” 的标记，不保证正确性。

我怎么感觉我好像都没写。

#208. function(?)：由于模 $p^k$ 意义下存在原根，所以此时解的个数只与 $3|\phi(p^k)$ 是否成立有关。而模合数的解个数等于模所有质因子幂的解个数的乘积，所以跑个类 min-25 的东西即可。

#224. minmex(?)：最短路图上支配树，则只需要找到最大的 $x$ 满足 $0\sim x$ 形成一条自上而下的链。线段树维护区间是否形成这样一条链，以及如果形成，链的最高点和最低点。

#240. Communication Network(?)：感觉和 “WC2019 数树” 差不多，就是最后树形 dp 的时候再加一维状态？

#248. Ghost domino(?)：考虑按 $W_i$ 从小到大加点，求出经过该点的最长路径长度。如果是树则直接并查集。注意到只有加入环上的最后一个点时才变成基环树，因此加最后一个点时特判即可。

#256. Binary Search Tree(?)：感觉可以对朴素 dp 做线段树合并？

#264. 如果会出题就好了(?)：换根查询单点的 $f(x)$ 可以做到 $O(1)$。考虑将查询拆成两部分，一部分的 $f(x)$ 不改变，直接来；另一部分考虑轻重链剖分，重链直接维护，轻边暴力跳。

#268. Sequence(?)：单调栈 + 经典维护前 7 位查询后 7 位，应该可以做到 $O(2^7\times n)$？

#272. Find a city(?)：用 $n - 1$ 次查询求出可能有 $n - 1$ 个出度的点；用 $n - 2$ 次查询求出可能有 $n - 2$ 个出度的点；然后对两个点分别 check 一遍。总操作次数 $\leq 4n$。

#276. Fierce Storm(?)：考虑保留安全系数 $\geq v$ 的点做避难所，求出合法的概率。可以做朴素 $dp(0/1, u)$，然后动态 dp 优化。

#296. Tree & Derangement(?)：感觉就是 loj - 6289？但是不知道 $O(n\log^3 n)$ 过不过得了。

---

A(2014 ACM-ICPC World Finals)

A - Baggage：首先注意到答案有平凡下界 n：考虑相邻的相同元素个数，初始为 0，终止为 2n - 2，每次操作最多增大 2，且第一次最多增大 1。观察样例，猜想下界一定可达。然后特判 n = 3，根据 n mod 4 分四类讨论，可以先构造 n = 4k 的情况，再在此基础上改一些细节得到其他情况。具体构造方法可见代码。

B - Buffed Buffet：离散情况是个平凡的背包 + 斜率优化。连续情况即最大化 $\sum(t_i X_i-\frac{\Delta t_i}{2}X_i^2)$，满足条件 $\sum X_i=S,X_i\geq 0$。取最优解时，对于所有 $X_i\neq 0$ 的 $i$ 均有 $t_i-\Delta t_i X_i$ 相等，不妨设为 $p$，此时还应满足对于所有 $X_i=0$ 的 $i$ 有 $t_i\leq p$。注意到 $t_i-\Delta t_iX_i$ 单调递减，因此一定是 $t_i$ 最小的几个满足 $X_i = 0$。那么枚举一下哪些 $X_i = 0$，注意可能会有 $\Delta t_i = 0$ 的情况。

C - Crane Balancing：求多边形的重心：拆成若干三角形，三角形的重心易求，质量正比于面积（面积为负也是对的，其实就是叉乘），然后做个类似带权平均数。注意如果重心在外而货物在边界上无解（因为货物不可能无穷大）。

E - Maze Reduction：两个点不等价当且仅当度数不同，或它们的边序列的循环移位都不对应等价。两条边不等价当且仅当它们的终点度数不同，或者它们同时往后数的第 $i$ 条边不等价。从平凡的不等价边开始推即可得到所有等价关系，直接时空复杂度 $O(n^4)$ 就可以过了（也有可能有更紧的时间复杂度分析）。

F - Messenger：记 $f(i,j)=t_i+d_{i,j}-t_j$ 表示邮递员从 $i$ 点走到 $j$ 点是否可行，如果可行，则显然 $f(i,j)=0$。注意到 $f(i,j)$ 关于 $i, j$ 单调，因此可以二分 $O(\log)$ 找到以某个点为起点/终点对应的终点/起点。考虑路径为两条线段的情况，列方程解发现是 邮递时间 是关于 出发时间 的对勾函数。由于单调，原本的两条路径可以 $O(n\log n)$ 的时间内剖成若干组 “两条线段” 的形式。但是明明对勾函数可以直接求最值，为什么我还要去写个三分变成两个 log 然后还被卡 TLE 了两次。

G - Metal Processing Plant：给定 D(A), D(B) 后（不妨假设 D(A) < D(B)）只需要 2-sat 判定，且没有边同时依赖于 D(A), D(B)。
从大到小枚举 D(B)，当且仅当 D(A) 小于环上最小边时，环才会出现，因此转化为 “求最大的不合法环的权值，其中环的权值定义为环上的最小边”，可以 floyd。
考虑进一步优化，实际上只有 $O(n)$ 个 D(B) 值会改变 floyd 的取值（考虑 > D(B) 的边的实际含义：边的两端不能同属一个集合），因此可以做到 $O(n^3)$。

H - Pachinko：考虑先求出 $f_{i,j,k}$ 表示从 $(i,j)$ 出发，第一次走到 $i+1$ 行是 $(i+1,k)$ 的概率，同理求出 $g_{i,j,k}$ 表示从 $(i,j)$ 出发，第一次走到 $i-1$ 行是 $(i-1,k)$ 的概率，都可以用高消在 $O(hw^3)$ 的时间内搞定。之后可以求出 $p_{i,j}$ 表示第一次走到第 $i$ 行是 $(i,j)$ 的概率，再利用 $f,g$ 就可以高消算出第 $i$ 行的答案，这部分时间也是 $O(hw^3)$。好像 $\epsilon$ 调小了，然后就被卡了次精度。

I* - Sensor Network：最大团啊，最大团不是 npc 问题吗，咋做啊。要不直接随机排列跑，反正 n 这么小。诶诶诶！它怎么就 AC 了呢。反正就是随机做，不会证正确性。
注：这道题存在合理的多项式算法。之后我大概会补上（大概，嗯）。

K - Surveillance：将环变成两倍长度序列，去掉被包含的区间（为了方便，显式地去掉更好）。则选定一个区间，最优的下一个区间是固定的，于是可以倍增求以每个区间为第一个区间的最小覆盖代价。

L - Wire Crossing：基本是个平面图转对偶图的裸题（mark 一份链接），不过注意这个平面图不一定连通 然后就被卡精度卡到怀疑人生。

---

B(2015 ACM-ICPC World Finals)

B - Asteroids：让一个多边形固定不动，算出相对速度。以速度方向为水平方向重新建轴，可以将 “凸多边形面积交” 拆解成若干组 “两个水平运动的梯形面积交”，可以进一步差分成 “两个半平面的交”。由此可知面积交是一个关于时间的分段二次函数，分类讨论 / 插值求出每一段的解析式即可。注意擦边也算相交（即使相交面积为 0）。

E - Evolution in Parallel：考虑按长度从大到小处理，假设已经有两组子序列降列，如果当前串两组都不能加入，则无解；如果只能加入一组，直接加；否则找到之后第一个不是当前串的子序列的串，则贪心地把中间的串与当前串放在一组里，这样一定不劣。因此只需要做 $O(n)$ 次子序列判定。

G - Pipe Stream：二分为啥不行，因为到达终点后没法区分。不过贪心地在能敲的时刻马上敲是对的。考虑决策树，叶子为长度 $\leq t$ 的区间，那么考虑贪心地将叶子设为 $[v_1,v_2-kt],\dots,[v_2-2t,v_2-t],[v_2-t,v_2]$。“到达终点后没法区分” 这一条件对应在决策树上，即相邻叶子必须某一深度之前分开，那么上面的叶子取法可以让这个深度限制尽量松。由于答案为 $O(\log)$ 级别所以直接暴力枚举，把当前深度必须分离的叶子分离出去，如果不够则无解；否则判断叶子个数是否超过所需个数，如果超过则找到答案；如果没超过，则每个叶子又可以裂成两个新叶子。

H - Qanat：可以发现两个井相邻之间存在分段点，左边走左井，右边走右井。差分距离 $d_i = x_{i+1}-x_i$，则有 $\sum d = w$，且代价是关于 $\{d_i\}$ 的二次函数。考虑拉格朗日算子法，变成线性方程组，发现有点规律，于是就过了。感觉应该有更高妙的做法（找规律找得我快吐了）。

J - Tile Cutting：$f_k = \sum_{a+b=k} \sigma(a)\times \sigma(b)$，直接 ntt 可过。

K - Tours：如果两条边所在的简单环集合相同，则称它们等价。题目的充要条件即 “所有等价边类内部每种颜色的边数量相等”，那么只需要取等价边集合大小的 gcd 即可。求等价边集合可以 tarjan 的时候暴力找，时间复杂度 $O((m+n)n)$。

L - Weather Report：哈夫曼树，把初始权值相同的放在一起。

M - Window Manager：其他命令暴力模拟检验。对于 move，不妨只考虑水平向左移动的情况，其他三种同理。将窗口按左上角横坐标从小到大排序，则前面的窗口一定被后面的窗口撞，从后往前扫并求出每个窗口第一次被碰撞的时间，同理求出第一次碰撞左边界的时间即可。注意像素是有面积的格子而不是格点（好像这是常识）。

---

C(2016 ACM-ICPC World Finals)

A - Balanced Diet：可以发现约束是线性规划形式（变量 $x_{i,j}$ 表示第 $i$ 天是否吃第 $j$ 颗糖），因此转化成最大流，贪心模拟增广。如果从左往右进行了 $\sum a_i$ 次增广仍然有解，则之后也一定有解（注意原序列长度 $>\sum a_i$ 仍然可能无解）。

B - Branch Assignment：先最短路。可以贪心地让同一个组里的值域连续（一定不劣），所以变成排序后区间划分。之后就决策单调性（类似于 CF321E/bzoj5311）。好像不用带权二分直接 $O(bs\log b)$ 的决策单调性也可以过。

D - Clock Breaking：对着题意模拟。

F - Longest Rivers：对于河流 $i$，最优肯定把它延伸到根，然后得到若干个 “子树 + 单边”。考虑怎么求一个的最大贡献，先看它内部所有河流是否都能 $\leq d_i$，如果可以，则最优情况应该是取儿子中最短的河流；如果不可以，看是否存在一个子树不能全部 $\leq d_i$，如果有，那就把不合法的河流引上来，该结点就没有影响；否则，至少要删去一个河流。那么每个结点的贡献都是独立开来的，分叶结点和非叶结点讨论。

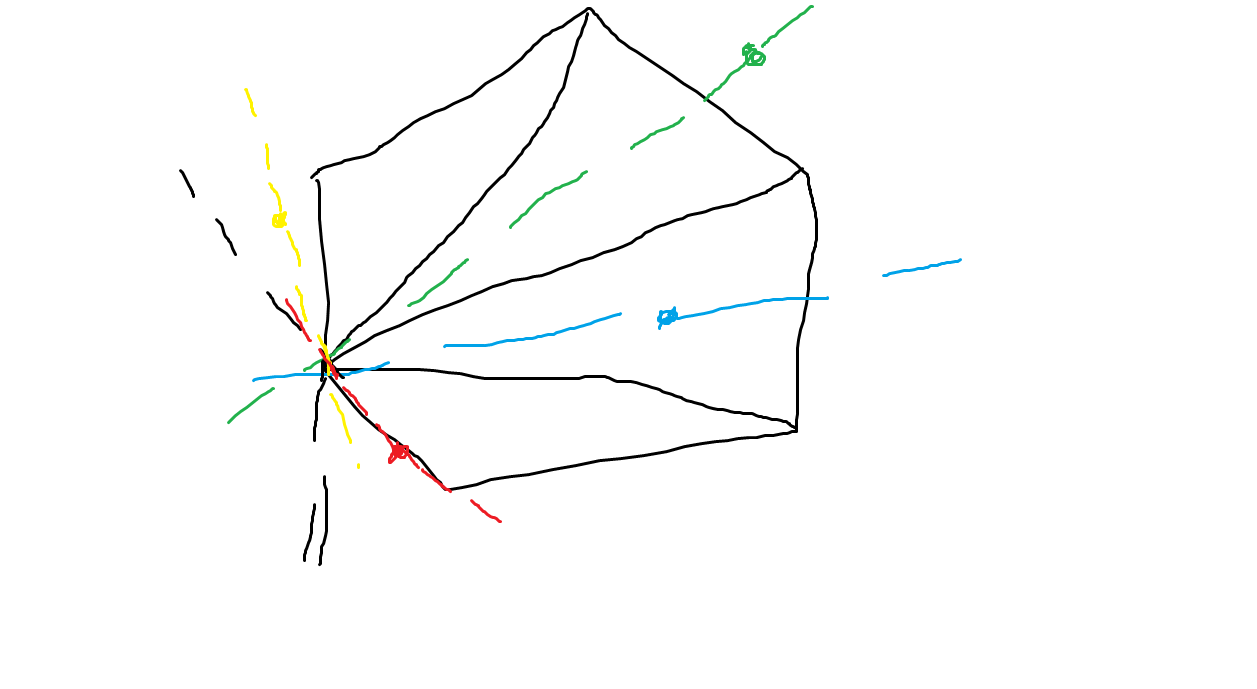
J - Spin Doctor：把 $(a_i,b_i)$ 当作坐标，对 $c_i = 1$ 的点求凸包，则答案即在凸包上旋转卡壳时包含的最少点数，事实上只需要求 $c_i=0$ 的所有点是否在凸包内，以及在凸包外的点与凸包的两条切线斜率。可以如下图 终于肯画图了 一样三角剖分，先二分找到每个点所属三角形，由此可判是否在凸包内。然后分两边三分（或者说二分斜率）找切点即可。特判凸包点数小于 3 的情况；特判下图中的黄点（切点是三角剖分的基准点）与红点（共线）所属情况（不特判容易 WA 比如我就 WA 了 6 次才过）。

K* - String Theory：首先正确理解题意 发现 “k引用” 里面恰好包含 1 个 “(k-1)引用” 最优，枚举模拟即可。注意特判 “1引用”。

M - What Really Happened on Mars?：虽然是递归定义，但题目中有说明这个递归定义不会成环，也即阻塞关系形成 DAG。首先确定出直接阻塞关系。如果某任务现在的 “current priority” 已经大于某资源的 “priority ceiling”，则它们不会形成阻塞（最终的 “current priority” 一定不会更小）。如果某任务与其他任务是否阻塞已经明确，则它的 “current priority” 不再改变，用该值更新其他任务即可。如果逐个命令模拟可能会 TLE（也有可能是因为我实现方法太垃圾），可以考虑记录阻塞关系是否改变，如果不改变就不需要重新计算。

---

D(2017 ACM-ICPC World Finals)

A - Airport Construction：最长线段一定经过两个顶点，枚举并尝试求解。相当于判定是否两个点连线上的点都在多边形内（如果不是则不合法），与求两个点向外最近的不在多边形内的点。用射线法判点是否在多边形内的思想，让射线始终在两点所在直线上，即可 $O(n)$ 求解。总复杂度 $O(n^3)$。

B - Get a Clue!：枚举 + 状压（我甚至怀疑直接暴力枚举都能过）。

D - Money for Nothing：决策单调性，注意决策区间有范围，用单调栈二分要好写点（之前做过）。

G - Replicate Replicate Rfplicbte：如果没有 bug，则上一个状态的左右上下边界一定是当前状态的边界往内缩 1 单位，那么总可以从左上到右下推回上一个状态，且是唯一的。如果有 bug，只需要分别找到第一个不合法的行、列，将对应的元素修改，然后再 check 一遍即可。

J - Son of Pipe Stream：令 $f'=vf$，则流量守恒变为 $f'+w\leq c$，只需最大化 $F'^aW^{1-a}v^{-a}$。
注意到最优点 $(F',W)$ 总是在线段 $F'+W=maxflow(F'\in I)$ 上取，因此目标函数 $F'^a(c-F')^{1-a}$ 是凸的，三分即可知最优点。
结果发现最难的是构造方案，主要是两种液体必须同向流动。先跑出最大流，将所有流量为正的边容量设为当前流量，流量为负的边容量设为 0，然后再从汇点向水源点退流，则剩下的流量即 flubber，流量的差值即水。

K - Tarot Sham Boast：（以下都是猜测，全部不会证）当 $n$ 足够大时可以用经典概率生成函数，发现 $\sum_i [s_{1\dots i}=s_{m-i+1\dots m}]\times \frac{1}{3^i}$（即第一次的期望）越大在越后面。当 $n$ 较小的时候，比较短的 border 用不到（可以根据概率生成函数发现这一性质），那么只比较前 $n-m$ 大的 border 即可。

L - Visual Python++：扫描线，从左往右，自下而上。扫描到一个右下角，该右下角必定与竖直距离最接近的左上角匹配。新匹配的矩形会产生一些限制，可以拆解为 “矩形正右边的 右下角 只能匹配矩形右边的 左上角” 与 “矩形正上方的 左上角 只能匹配矩形上方的 右下角”，简单维护一下。

---

E(2018 ACM-ICPC World Finals)

C - Conquer the World：模拟费用流。

D* - Gem Island：简单算算可知所有情况可能性相等（目前不知道组合意义是啥）。那么可设 $f_{i,j}$ 表示把 $j$ 颗宝石分给 $i$ 个人，前 $\min(r,i)$ 大之和的期望。转移类似于整数拆分，枚举多少人有宝石，因为可能性相等所以概率用组合数算（目前也不知道 double 的精度为啥能过）。

发现此题还有时间复杂度更优的解法，补充在这里：

枚举前 $i$ 大 $\geq x$，后 $n - i$ 个 $< x$，则容斥可得方案数为 $\sum \binom{n}{i}\sum_{p=0}^{n-i}(-1)^p\binom{n-i}{p}\binom{d-(p+i)x+n-1}{n-1}$，贡献为 $\min\{i, r\}$。答案为：

$$\frac{1}{\binom{d+n-1}{n-1}}\left(r + \sum_{i=1}^{n}\sum_{p=0}^{n-i}\min\{i, r\}\binom{n}{i}\binom{n-i}{p}(-1)^p \left(\sum_{x=1}\binom{d-(p+i)x+n-1}{n-1}\right)\right)$$

相信大家的公式恐惧症又犯了。

记 $f_{i+p} = \sum\min\{i, r\}\binom{n}{i}\binom{n-i}{p}(-1)^p$，再记 $g_{i+p} = \sum_{x=1}\binom{d-(p+i)x+n-1}{n-1}$，则答案为 $\frac{1}{\binom{d+n-1}{n-1}}(r + \sum f_i\times g_i)$。考虑怎么求这俩。

首先 $f_1 = n, f_k = \binom{n}{k}\binom{k - 2}{r - 1}$，至于为什么 不会证，告辞（其实会证但是证得很麻烦 qaq）。

然后 $g_k = \sum_{x=1}\binom{d-kx+n-1}{n-1} = \sum h_{kx}$ 可以狄利克雷前缀和做到 $O(n\ln\ln n)$。

因此总时间复杂度 $O(n\ln \ln n)$。

E - Getting a Jump on Crime：按题意模拟，注意边是有向的 难点在解二次方程组。

H - Single Cut of Failure：冷静分析一波，发现连接对角线必然是合法解。所以问题简化为是否可以一条线切断所有，转化到区间上即一个区间与所有区间同时严格相交（不包含、不相离），随便判一判即可。

I - Triangles：读入比较麻烦。处理好读入的各种 cases（比如 c = 1）后，可以将问题转化为求 $a_y\leq x \leq y \leq b_x$ 的二元组数量，直接 $O(rc\log c)$ 就可以过了（虽然我自己跑了 5s，不清楚是否有更优解）。

---

F(2019 ICPC World Finals)

B - Beautiful Bridges：观察到时限 10s 且 $n\leq 10^4$，所以直接暴力来。如果固定右端点且只考虑拱桥的右半部分是否合法，则左端点可取的范围是一个区间；对于左端点同理。于是就可以 $O(n^2)$ 暴力 dp 了。

F - Directing Rainfall：对横坐标离散化，考虑从上往下扫描每个挡板，并对于每个横坐标从上面到达当前点的最小代价。则一个挡板的影响可以看作 “区间执行 $a_i=\min\{a_j|j\in[l,i]\}$ 或 $a_i=\min\{a_j|j\in[i,r]\}$” 与 “区间加”，线段树维护即可。但是直接扫描不现实，考虑处理挡板之间关于上下遮挡关系的拓扑序（注意它是偏序但不是全序）。从右往左扫描，在加入某个挡板的右端点时求出此时它上下最近的挡板，并连边，最后跑拓扑排序即可。

G - First of Her Name：trie 上查询子串出现次数。广义后缀自动机模板题。

I - Karel the Robot：考虑求出 “当前格子 $(x, y)$，方向 $d$，执行第 $i$ 个 program（可能是某个 program 内部的子 program）” 最终到达的点（或者说无限循环），只需要在模拟时判断是否到达曾经到过的点即可。总状态数量 $O(40\times 40 \times 4 \times (26 + 10) \times 100)$，可以接受。

J - Miniature Golf：考虑每个人分别计算答案，其他每个人和这个人的大小关系可以分成 $O(h)$ 段，总共 $O(ph)$ 段，每一段取最小值即可，时间复杂度 $O(p^2h)$。

K* - Traffic Blights：问题转化为随机非负整数 $x$，同时满足若干形如 $x\bmod m_i \neq a_i$ 的限制的概率。注意到若 $m,n$ 互质，则 $x\bmod m \neq a$ 与 $x \bmod n \neq b$ 的概率是独立的。如果所有概率独立，就可以分开维护每种限制的概率，最后相乘即可。
考虑让这些概率独立，思路是，用全概率公式将其拆成若干条件概率之和，使得条件概率是独立的，于是分开维护条件概率即可。一个直观想法是利用 “一个数最多包含一种 $>\sqrt{a}$ 的质因子” 的性质，设条件 $i$ 为 $x \bmod 64\times81\times25\times49=i$，这样得到的条件概率的含义是 “模 $>\sqrt{a}$ 的质数”，显然它们两两互质，即它们的概率独立。
但是显然效率不够。考虑利用性质 “一个数的质因子幂最多有一个 $>\sqrt{a}$”，这样可以设条件 $i$ 为 $x \bmod 8\times9\times5\times7=i$，得到的条件概率的含义是 “模质数 $\leq a$ 的最大幂”，它们也两两互质，而且效率更高。

---

G(2017-2018 ACM-ICPC Northern Eurasia (Northeastern European Regional) Contest (NEERC 17))

F - The Final Level：第一步横纵坐标距离最大减少 $(n-1)$，之后每一步横纵坐标距离一个减少 $(n-1)$，一个减少 $n$。因此能够走到的位置即一个正方形挖去四个角，可以二分（或者直接枚举）求出最小操作次数。构造时让横纵坐标差得比较远的减少 $n$，另一个减少 $(n-1)$，判断一下减少 $(n-1)$ 是否会走过头。

G - The Great Wall：二分 + 平衡树/离散化后树状数组。

I - Interactive Sort：本质其实是排序，考虑用快排的思想，只需解决划分的问题。可以从奇数里面随机选来划分偶数，从偶数里面随机选来划分奇数。但这样区间不一定划分均匀，可以考虑先跑左边，然后把左边无法确定的元素塞到右边一起处理。不过这样次数会略多，可以考虑把之前询问过的答案存下来，这样就可以跑过了。

J* - Journey from Petersburg to Moscow：考虑让不合法的路径变得不优。边数 $<k$ 的路径直接跑最短路。对于边数 $\geq k$ 的路径，考虑枚举下界 $p$，只对权值 $\geq p$ 的边计算费用。此时可以将 $\geq p$ 的边权减去 $p$，求出最短路后加上 $k\times p$。

K - Knapsack Cryptosystem：当 $n$ 比较小时用 meet in the middle；当 $n$ 比较大时则 $a_1$ 一定很小，直接枚举 $a_1$ 然后 check 是否 $a$ 序列合法。（草，原来 $a_1r=b_1$ 在模合数意义下可以有多个 $r$。感觉说出这种话就像自己没学过数论一样，啊的确没学过。）

L - Laminar Family：考虑把路径放在最高点 lca 处。对于根 x，如果没有路径经过它，递归到子树。否则取出最长路径，则其他路径一定是它的子集，然后转化成链上的问题，即判断是否存在区间严格相交。之后删掉这条路径继续递归子树即可。

---

H(2016-2017 ACM-ICPC Northeastern European Regional Contest (NEERC 16))

B - Binary Code：trie 优化 2-sat 建图（之前写过，不过不知道为啥在某 oj 上过不了）。

C - Cactus Construction：用圆方树处理，每次保留最少限度的颜色（比如之后不会再连边的点设为同一颜色），发现最多确实只有 4 种颜色。

D - Delight for a Cat：经典费用流，可以线性规划转，也可以直接建。（为什么 long long 转 int 没报警告啊，为什么这会输出不合法的解啊）

G - Game on Graph：按强连通缩点后拓扑序从后往前的顺序分别处理每一个强连通分量，特判无自环的单点。
先判是否无限，对于 Gennady 如果存在一个后继无限则无限，对于 Georgiy 如果所有后继无限则无限。如果不能根据已知信息判断是否无限，则可以推断它一定无限（对于两名玩家而言，最优策略都是走另一个无法确定的点，那么就会在无法确定的点之间循环）。
然后再判胜负，类似地，存在一个后继必败则必胜，所有后继都必胜则必败。无法确定的点 Gennady 必胜，Georgiy 必败（宁愿输也不会循环）。
两个过程都可以用队列处理，目前不清楚是否可以把两个过程缩成一个。（我怎么就过了，我又改了哪里，这些不都是等价改动吗.jpg）

K - Kids Designing Kids：去掉周围的空格。如果矩形 1 第 1 列没有和矩形 2 的第 1 列重合相消，那么矩形 1 第 1 列一定等于矩阵 3 的第 1 列。同理可得共 4 种情况，还有 1 种情况即矩阵 1, 2 的第 1 列第 1 行重合。模拟即可（我自己写的模拟方法是存所有 * 的坐标，好像比别人的长一倍，不知道另有什么高妙的方法），注意矩形 3 可以全空。

L - List of Primes：不难猜到当字符数量 $\leq 10^{18}$ 时素数之和并不大，打表可以验证素数之和最大是 2100 ~ 2200。先找到 $[l, r]$ 之中的第一个方案，然后不断地寻找下一个方案。背包预处理 $f_{i,j}$ 表示使用 $\geq i$ 的素数凑出和为 $j$ 的方案数，然后逐位贪心即可。

M - Mole Tunnels：还是费用流。只要建出反向边，每次跑最短路即可得到最小费用最大流。维护一下反向边的贡献即可，因为原树高 $O(\log)$ 所以直接来。注意反向边是由 $1\to-1$，所以对应在边权上应该是 $\pm 2$。

---

I(2015-2016 ACM-ICPC Northeastern European Regional Contest (NEERC 15))

B - Binary vs Decimal：直接暴搜，可以把 $(10^p-2^p)$ 按 lowbit 从小到大排序，因为模数是 2 的幂所以可以根据 lowbit 剪剪枝，效果十分显著。可以通过打表把二进制位数确定下来再搜。

C - Cactus Jubilee：如果删非环边，原图裂成两个连通块，合法边数量即连通块大小之积。如果删环边，新图仍是仙人掌，考虑建出圆方树，则圆圆边形成的连通块内部都可以连边（但不能连重边）。新图和原图只相差删掉的边所在环，维护一下即可。

D - Distance on Triangulation：考虑经典分治，找到一条对角线使得它尽量均分多边形，则对角线两边的点之间任意路径一定经过对角线的某个端点（同 ZJOI2015 旅行者）。虽然我并不知道为啥总能找到这样一条尽量均分的对角线。

H - Hypercube：不清楚正确的判别姿势是什么。不过你可以考虑类比六个面折成正方体的方法：将六个面平铺在 xy-平面，固定一个下底面，把每两个相邻的面 “向上” 折起，最后如果没有两个面重合则一定有解。推到四维情况，可以用中心点 + 法向量形式表示正方体，然后类比二维咋折的，折出来过后判是否有中心点重合即可。

J - Jump：如果有一个 n/2 的询问，可以同时给两个位置取反并再次询问，以此判断两个位置是否同时和答案相同，那么只需要最多 $n+1$ 次询问即可问出来。考虑怎么找一个 n/2 的询问 发现不会做，于是随机化。随机一个 01 串，直到返回 n/2 为止，概率为 $\frac{\binom{n}{n/2}}{2^n}$。

K - King's Inspection：如果出边唯一，则哈密顿回路必然包含这条出边。暴力枚举出边不唯一的，用并查集判是否形成哈密顿回路。

L - Landscape Improved：二分 + 单调队列 check。

---

J(2014-2015 ACM-ICPC Northeastern European Regional Contest (NEERC 14))

C - Cactus Generator：在递归时给定首结点与尾结点的编号，最后把编号改一改，使得满足 1 号点是首结点、n 号点是末结点，这样就可以 $O(|E|)$ 构造仙人掌。对于要合并的图列表，特判第一个图和最后一个图（当然还要特判只有一个图的情况），然后按照规则合并即可。建出图后跑个欧拉路，不知道有没有更简单的做法。

E - Epic Win!：如果已知对手的当前状态，则可以构造一个 $O(n)$ 的 $\rho$ 形图，使得之后一直赢。如果对于两个点构造出的 $\rho$ 形图同构，则认为这两个点等价。尝试用有限步区分所有等价点，如果当前对手可能的状态集合存在某些状态输出不一样，则自己的自动机随便输出即可区分；否则，输出能够赢对手的（即 $\rho$ 的第一步）。如果连续 $n$ 次都无法区分，则它们等价。

G - Gomoku：自己手动实现一个交互库，然后和人工智障愉快玩耍，顺便人脑构造必胜策略（你玩五子棋还玩得过我？）。代码给出了一份参考策略 因为策略有些复杂就不放上来了。

H - Hidden Maze：众所周知，像这样随机生成的树直径长 $O(\sqrt{n})$（当然你不能像我一样老老实实就开到刚好 $\sqrt{n}$ 的空间对吧）。于是从小到大枚举边，将小于的标为 -1，大于的标为 1，相当于求有多少权为 0 的路径经过枚举的边，怎么暴力怎么维护。（yhn 那天还来问过我咋证明，但我也不会，然后他说他问了周围一圈没一个会的）。

I* - Improvements：只需要选出一个最大合法子序列即可，然后你发现合法的飞船子序列与一个编号先增后减的飞船子序列一一对应，然后 LIS 就完了。草哦为什么我这么傻逼。

---

K(2013-2014 ACM-ICPC Northeastern European Regional Contest (NEERC 13))

A - ASCII Puzzle：想题五秒钟，读题半小时。本质就是正常的拼图，题目所给的限制其实保证了你可以区分拼图是否在边界上，这样搜索量在 $n = 4$ 时也最大只有 $2^4\times 4!$。为了代码简单我删去了一些剪枝（结果一开始还 TLE 了）。

C - Cactus Automorphisms：建圆方树，找重心（一定没有对称边）。对于方点，如果不是重心，则只有两种同构方式（分别为正着摆放儿子、倒着摆放儿子），因为有顺序所以做两个字符串 hash，取较小值；如果是重心，则可以翻转儿子序列 + 旋转儿子序列，找到所有可能的字符串 hash 判一判。对于圆点，类似于树同构计数（草，我怎么把 “将 $x$ 的方案数摊到 $x$ 的质因子上” 这一步写错了）。

D - Dictionary：考虑某个串的贡献，它的前缀可以重复利用另一个串的中间部分，除去前缀剩下的就是它自己的贡献。因此求出每个串 si 重复利用另一个串 sj（可以是空串）的中间部分，最大能重复利用多少。然后变成最小树形图问题，不过还要输出方案，可以考虑用递归实现朱刘算法，这样比较方便拆零环。得到最小树形图方案后再建 trie 跑一跑即可。

关于最小树形图咋做。WC2020 员交有一个 “优先内向树扩张算法”，但我没看懂觉得不方便输出方案，所以 mark 一下朱刘算法：

每次找到每个点的最小出边，如果无环则找到解；否则把环缩点，每个点的所有出边减去最小出边（可以理解为 “替换当前出边” 的代价），然后重复该过程。

优化使用可并堆 + 并查集即可。

G - Green Energy：如果塔落在地形产生的阴影里，则可以将其挪到产生阴影的最高点，一定不劣。考虑以阳光方向为 $x$ 轴建正交系，则塔的覆盖范围转化为 $y$ 轴上的动线段，地形转化为塔对应线段的左端点范围区间。可以贪心地把高塔的左端点往右放，矮塔的左端点往左放。

H - Hack Protection：固定右端点，往前 and 只有 $O(\log A)$ 种取值。求异或前缀和，对于每种取值在动态开点线段树上查询区间和即可。

I - Interactive Interception：一共有 $(v+1)\times (p + 1)$ 个决策点，每次尝试找到使得决策集合尽量均分的询问。为了方便，将询问的左端点设为最左边的点，这样子所有决策点可以分成 $O(v)$ 个区间，然后枚举一下右端点在哪里即可。

K - Kabaleo Lite：枚举你的对手们想要最大化的，则 $n$ 个堆可以分成 3 类：你想要最大化；你对手想要最大化的；其他的。再枚举你选择这 3 类中的哪一类，判断是否合法。细节较多（比如最后一个人的颜色必须存在于场上）。

---

L(2017-2018 ACM-ICPC, Central Europe Regional Contest (CERC 17))

B - Buffalo Barricades：如果仅考虑形态而不考虑先后顺序，可以从右往左扫描线维护答案。但可能出现先询问外面再询问里面的情况，可以考虑根据包含关系建树（在扫描线的时候建），然后从大到小用并查集把当前点的答案向上合并。

C - Cumulative Code：对 $m$ 的大小分类。$m$ 较小的暴力查；$m$ 较大的公差一定小，做个 dp。总时间复杂度 $O(2^{k/2}\times q\times \log A)$，听说可以少个 $O(\log A)$，但我不会。

D - Donut Drone：倍增不方便维护，考虑找循环节。平衡 “每次询问暴力找循环节” 与 “每次维护出修改后所有位置的循环节” 的时间，考虑维护第一列跳 c 步（一定又回到第一列）到哪一行，单次询问利用维护的信息可以做到 $O(R+C)$。
修改看作改点的 next，此时对于某一列影响到的点一定是连续的，所以可以 $O(R+C)$ 维护第一列哪些行的信息变化。
总时间复杂度 $O(MR+MC)$（WA 的原因：直接修改第一列的 next 时出问题）。

E - Embedding Enumeration：以 1 为根时每个点最多 2 个儿子。记 $f_{i,j}$ 表示以 $i$ 为根的子树中，$i$ 所在的行比另一行少 $j$ 个连续的空格（其实应该配张图，但是我懒.jpg）。分情况讨论 $f$ 的转移，发现大多数时候用到的是 $f_{i,0}$，只有一条链时才会用到其他的。于是把一条链的单独拿出来做 dp，求出所有的 $f_{i,0}$ 即可。时间复杂度均摊下来是 $O(n)$ 的。

I - Intrinsic Interval：从左往右扫描并单调栈 + 线段树维护 $f_l =(\max-\min)-(r-l)$ 是否为 0，如果是则 $[l, r]$ 为连续段。由于 $f_l\geq 0$，所以等价于维护 $f$ 的最小值。一种方法是离线，利用连续段的交仍是连续段的性质，可以先找到最小可能的右端点，再找最大合法左端点。

也可以增量法建析合树求 lca（以下没实现过，不清楚口胡得对不对）。

考虑维护当前析合树森林的根构成的栈，如果当前点能成为栈顶的儿子（此时栈顶一定是合点，记得还要判是否单调）就接上去。

否则先用 $f$ 判断是否可以往前合并成更大的连续段，如果不行直接停止；如果可以，不断弹出栈顶直到成为连续段，新建点并向这些元素连边。如果新点只有两个儿子则为合点，否则为析点。

每次更新当前点并重复上述操作。

K - Kitchen Knobs：因为 7 是质数，如果数位不全相同，则最优方案唯一。求出转动次数并差分，问题转化为每次可以选择两个一加一减，或者选择一个加，全部变 0 的最少操作。可以转化为选出尽量多不交集合，满足每个集合内 $\sum x\bmod 7 =0$。注意到贪心地选出 $\{x,7-x\}$ 作为集合总是不劣的，因此 1 和 6、2 和 5、3 和 4 之间可以分别贪心地删去一种，最后只剩最多 3 种数，dp 即可。

L - Lunar Landscape：注意到坐标范围比较小，搞点类似于斜着二维差分的东西即可 $O(A^2+N)$ 的时间内求出每个单位格的贡献。

---

M(2016-2017 ACM-ICPC, Central Europe Regional Contest (CERC 16))

B - Bipartite Blanket：hall 定理 + two points。

E - Easy Equation：苦思冥想一小时，打表出解五分钟。首先注意到有一组平凡解 $(1, k,k^2+k)$，考虑怎么根据一组解 $(a,b,c)$（无妨假设 $a<b<c$）扩展出其他解。如果知道扩展方法，hash 判重即可构造 $n$ 组互不相同的解。
注意到有二次方程 $a^2-k(b+c)a+(b^2+c^2-kbc-1)=0$ 成立，由韦达定理可得 $a'=k(b+c)-a$ 是另一零点，且它满足 $a' > b, a' > c$（由于 $k > 1$），所以 $a'$ 为正整数，有新解 $(b,c,kb+kc-a)$；同理也可推得新解 $(a,c,ka+kc-b)$。注意 $(a,b,ka+kb-c)$ 不一定合法，因为 $ka+kb-c$ 的正负无法确定。

I - Invisible Integers：从后往前依次放数，记 $f(i,p,j,q,s)$ 表示后面最近的朝左限制是 $i$ 且匹配了 $[0,p)$，前面最近的朝右的限制是 $j$ 且匹配了 $[q,len_j)$，当前还没有开始匹配的限制集合为 $s$。预处理 $g(i, j)$ 表示 $i$ 限制的下一个限制是 $j$ 时至少需要匹配 $i$ 中的 $[0,g(i,j))$，转移时有两类，一类是放数，它必然是两个限制之一的将要匹配的数；另一类是换下一个限制。状态总数 $O(2^{10}\times 10^4)$，总转移复杂度 $O(2^{10}\times 10^5)$，但它就是能过。

J - Jazz Journey：把所有点对分开处理，类似括号匹配的贪心。

L - Lost Logic：限制越多解越少，因此把所有合法限制加上，暴力枚举解个数是否 > 3。但是当我莽完交上去才发现 $m\leq 500$，注意到强连通分量个数 $\leq 2^3 = 8$，因此每个强连通内部连成环，最多只会有 $2n+64$ 条边。

---

N(2015-2016 ACM-ICPC, Central Europe Regional Contest (CERC 15))

C - Cow Confinement：考虑把牛到花的路径唯一化，即先尽量往右走，再尽量往下走。这样做的好处是，如果从右往左做扫描线，大多数路径都不会变化。维护时首先把新加入的矩形竖边界所在行清零，然后维护新加入的花的影响。如果矩形竖边是左边界，则矩形左下角还会对矩形下边界往上的点产生贡献，但是这样会算重，还要减去矩形右下角还会对矩形上边界往上的点的贡献（注意线段树的范围要开大点，否则会访问到非法位置）。

E - Export Estimate：大多数情况下删二度点后，其他点的度数不变，此时对于某张固定的图操作后点数为 $n-deg_2-deg_0$，边数为 $m-deg_2$。然而有一个例外，就是删出了自环。自环不被删，所以这对非二度点不影响（本来就不删它），但是对于一个简单环，它最后会变成单点单边，因此最后的点数与边数还要加上简单环个数。再并查集维护一下简单环个数（维护两个东西：点的最大度数，点数与边数之差）即可。

F - Frightful Formula：考虑计算贡献，$l_i,t_i$ 的贡献是平凡的。对于 $c$，它的贡献为 $\left(\sum_{i=0}^{n-2}\sum_{j=0}^{n-2}\binom{i+j}{i}a^ib^j\right)\times c$，可以将 $j$ 有关的项提出来，发现是 “下降幂 × 等比” 的形式，直接错位相减。

然而从组合意义出发（走格子），可以得到如下（我也不知道为什么）的式子：

$$\sum_{i=0}^n\sum_{j=0}^n\binom{i+j}{i}a^ib^j=\sum_{i=0}^{2n}(a+b)^i-\sum_{i=0}^{n-1}\left(\sum_{j=0}^{i}(a+b)^j\right)\times\binom{2n-i-1}{n}\times(a^{n+1}b^{n-i-1}+a^{n-i-1}b^{n+1})$$

感觉组合恒等式太头疼了，溜了溜了。

G - Greenhouse Growth：如果某一时刻相邻的植物高度相同，那么它们接下来将一直相同。因此只需要每次修改后找到新的相邻高度相同的植物，并将它们合并，可以用 链表 + 并查集 + set/带删优先队列 实现。实现时注意某次修改后可能有多次合并，比较麻烦。

I - Ice Igloos：暴力找到所有可能的圆心。不知道为啥本机过了交上去过不了了，改成 long long 才过。

J - Juice Junctions：显然最小割树，保证了最小割 $\leq 3$。最小割为 $0$ 或 $1$ 的情况是平凡的，考虑最小割为 $2$ 的情况，如果枚举源点 dfs 需要 $O(n^3)$（认为 n, m 同阶）的时间。但可以反过来枚举最小割中的一条边，删掉这条边后，任意新增的桥一定和这条边形成大小为 2 的最小割，这样就可以 $O(n^2)$。

L - Looping Labyrinth：称每个 $n\times m$ 为 “大块”，原点所在大块坐标 $(0,0)$。只考虑每个大块的边角连通块，则一个大块内部的总连通块个数为 $O(n+m)$。考虑在连通块之间连边，表示从连通块 $A\to B$，大块坐标对应变化 $(\pm 1,0)$ 或 $(0,\pm 1)$，则只要存在一条（不一定简单）路径从询问点到原点，使得路径对应的大块坐标与询问的大块相同即可。可以将其拆成一条简单路径 + 若干简单环，那么只需要先 $O(n+m)^3$ 求出有用的简单环，再将这些简单环合并（合并的方法可以考虑实际意义，发现是一个不定方程组）。
口胡到我自己都看不懂自己在写什么。

---

O(2014-2015 ACM-ICPC, Central Europe Regional Contest (CERC 14))

A - Parades：把路径放在 lca 处理，可以进行 dp，发现在每个结点处需要做一个一般图最大匹配，由于点度数 $\leq 10$ 所以状压即可。

B - Mountainous landscape：如果二分，则只需要查询区间凸包 + 二分求切线，但复杂度为 $O(n\log^3n)$。考虑直接线段树二分，则复杂度降为 $O(n\log^2n)$，可以通过该题。

E - Can't stop playing：考虑直接暴力。每时刻的状态一定是峰形，如果直接存则状态总数 $O(2^{26})$。考虑只存峰形的一半，另一半可以用总和减去一半，那么状态总数即 $O(2^{13}\times n)$。转移可以做到 $O(1)$，只需要知道最高 bit 与最低 bit 即可。

G - Virus synthesis：建出 PAM，对所有偶回文子串 dp。转移两种：一种从长度 ≤ len / 2 的偶回文后缀转移，倍增找即可；一种不是从后缀转移，则可以把两端去掉，因此就是 PAM 的父亲转移过来。不知道能不能线性。

J - Pork barrel：由 kruskal 的过程可知，给定下界后最小生成树唯一，且下界增加最小生成树的形态总变化量为 $O(m)$，于是可以用可持久化线段树维护。现只需考虑求出每次应该使用哪条边替换最小边，可以去求每条边换掉了哪条边，把换掉的那条边删掉，然后把新边加进去。可以发现按从小到大的顺序替换即可，扫一遍用 lct 维护即可（多测不清空，*****）。

K - The Imp：二分答案，判断最终答案是否可以 $\geq mid$。等价于是否可以选择 $k + 1$ 个物品满足 $v_i - \sum_{j\leq i} c_j\geq mid$。注意到物品顺序可以提前贪心排好（交换论证可得），因此排好序做 $O(nk)$ 的 dp 即可判断，总时间复杂度 $O(nk\log A)$。

L* - Outer space invaders：区间 dp，枚举最大的攻击在哪个时刻，它的贡献一定是 $\max\{d_i\},[a_i,b_i]\sub [l,r]$。

---

P(2013-2014 ACM ICPC Central European Regional Contest (CERC 13))

A - Rubik's Rectangle：把相互可达的 4 个格子（特判 n, m 为奇数的情况）一起处理，有 4 种翻转会影响它们，它们都会改变这 4 个格子之间的逆序对奇偶性。因此可以决定行列翻转次数的奇偶性，如果奇偶性合法则一定有解。输出方案有点麻烦。

D - Subway：输入看着有点麻烦。建出图后需要跑双关键字最短路，不过写完dijkstra发现边权有负的冷静一下发现 bfs 即可代替最短路的过程。

E - Escape：转化成 “先损失 $a$ 再收益 $b$” 的形式，将终点收益设为 $+\infin$，做树上贪心（即每次取出最优的点与父亲合并）判断最后是否需要先损失才能遍历完树上所有点（p.s.：延迟删除的堆一定要写严格偏序）。

H - Chain & Co.：把矩形按法向量方向分为三类，则每一类必须分到一起。于是只需要判某两类是否相容，这个随便模拟一下就好了。

J - Captain Obvious and the Rabbit-Man：如果找到一组 $b_{1\dots k}$，使得对于 $F_{1\dots k}$ 都满足 $F^{k+1}=\sum_{i=1}^{k}b_iF^i$，则有 $p(k+1)=\sum_{i=1}^{k}b_i p(i)$。由于 $F_{1\dots k}$ 是 $f(x)=x^{k+1}-\sum_{i=1}^{k}b_ix^i$ 的根，所以有 $x^{k+1}-\sum_{i=1}^{k}b_ix^i=x(x-F_1)(x-F_2)\dots(x-F_k)$，直接 $O(k^2)$ 展开即可。

---

Q(2017-2018 ACM-ICPC, NEERC, Northern Subregional Contest)

C - Consonant Fencity：枚举。

E - Equal Numbers：将数分为两类，一类是有倍数的，一类是没有倍数的极大值。两种情况：要么只动有倍数的，把这些数改成极大值；要么全部都可以动，把这些数改成所有数的 lcm，这种情况需要多操作一次。把这些数的出现次数从小到大排序然后贪心取即可。

F - Fygon 2.0：依大小关系建图，缩强连通，则 $k$ 即 DAG 点数，而 $C=\frac{cnt}{k!}$（其中 $cnt$ 是合法拓扑序数量，状压即可）。

G - Grand Test：如果存在不是单边或简单环的点双，则一定有解。构造方法即取出该点双的任一简单环，必然存在另一不属于简单环的路径从环上一点到另一点，这样就有 3 条路径了。

H - Hidden Supervisors：先给每棵树内部找个最大匹配（贪心地从叶子开始匹配），如果根没有匹配，则它可以与其他树中未匹配点匹配。考虑先将有匹配根的树与 1 号点所在树连接，然后尝试将未匹配根的树与 1 号点所在树中未匹配点连接。如果剩下 > 1 个没有匹配的根（此时一定没有未匹配的非根结点），可以把 1 号点所在匹配拆开，分别与两个未匹配根相连，消掉两个没有匹配的根。sort 如果传入一个非严格偏序关系会 RE 而不是 WA。

J - Joker：经典分块维护凸包，最优应该可以做到 $O(n\sqrt{n\log n})$。在凸包上二分时注意取较小的那个位置。

---

R(2016-2017 ACM-ICPC, NEERC, Northern Subregional Contest)

B - Boys and Girls：特判全为 B/G 的情况。设 cntB = cntG = cnt 表示极大连续的 B/G 段数，设 sumB, sumG 表示 B/G 的总个数，设 oneB, oneG 表示单独一个 B/G 成段的数量。列方程，发现可以先解出 sumB, sumG。于是枚举 cnt，求出 oneB, oneG 的范围判断是否有解。构造根据以上信息随便怎么构造即可。

D - Digital Addition：简单 dp，模拟判断决策是否可行。

E - Easy Reading：滑窗，当两张图点数相等时再判断是否同构，这样只会判 $O(l)$ 次同构。考虑将点排序，对 x,y 两维分别字符串 hash。为了让两张图左上角对齐还需要平移一个向量，发现这种 hash 是可以支持平移的。用平衡树维护一下 hash 值即可。

G - Gangsters in Central City：维护根的每棵子树内的所有点的 lca。

I - Integral Polygons：等价于求叉积之和为偶数的方案数。求一下叉积的前缀和，线性扫描 + 随便维护一下（不清楚为什么在 OJ 上过不了 现在好像过了）。

J - Java2016：不断取 $\max$ 几乎可以 100% 得到 255，利用宏大概可以对 $2^{13}$ 个随机变量取 $\max$，剩下的只需要搞个类似快速幂即可。

---

S(2015-2016 ACM-ICPC, NEERC, Northern Subregional Contest)

D - Distribution in Metagonia：只需要让构造出来的 3 的幂次严格递减即可。

F - Fygon：就硬模拟。不清楚怎么简单算，反正我写了个自然数幂和。

I - Insider's Information：考虑随机调整，依次考虑所有限制，以一定概率将排列修改成满足该限制（最多只需要交换一次即可）。最后判断是否有足够数量的限制满足要求，如果不够就再来一遍。不知道正确率咋算，看起来很优。

G - Graph：比较 trivial 的贪心。找到当前所有入度为 0 的点，从小到大依次加 “入边”（先不去确定入边对应的点），比较最大的入度为 0 与现在需要加 “入边” 的最大点，如果是入度为 0 的点大则直接加入拓扑序，否则拓扑序上一个点向需要加 “入边” 的最大点连边。

---

T(2014-2015 ACM-ICPC, NEERC, Northern Subregional Contest)

C - Combinator Expression：由于题目告诉你正规形式保持不变，而只有 "K" 算子才会删掉其他算子，所以只要 "K" 算子删掉的尽量多即可。然后你发现从左往右执行算子一定最优（如果先内部执行算子的话，"K" 算子能够删掉的会变少），建树出来模拟即可。

E - Expression：首先你得会把正则表达式转 $\epsilon-NFA$（注意它的参数可以是空的正则表达式）。预处理 起始结点匹配到某个点 / 某个点匹配到终止结点 的最短串以及对应方案。然后在上面跑 $O(|E|\times|S|)$ 的 dp 求出最短长度，注意不能存 $O(|E|\times|S|)$ 的方案，但是中间部分是已知（即需要匹配的模式串），所以也不需要存。MLE 原因：vector 的 clear 函数不清空内存。

F - Fragmentation：离散化，缩相同连续段。则 $a_{i}$ 与 $a_{i+1}$ 之间不切断的充分条件为 $a_{i+1}=a_i+1$，且每对相邻权值 $(k, k + 1)$ 在原序列中只能对应不切断一个地方。如果 $(k-1,k),(k,k+1)$ 在原序列中不切断的地方相邻，则 $k$ 的出现次数必为 1。因此出现次数为 1 的权值之间可能会有约束（选 $a$ 不能选 $b$）。构造方案时从左往右，先处理出现次数为 1 的权值，具体看代码（你马的，少一行 break 调 1h）。

H - Hiking in the Hills：从一个面走到另一个相邻面，一定走两者交集的最低点最优（这个点一定是顶点）。路径上最高点一定是在面面之间产生，而不是在面内产生（因为总是走直线），因此变成最小生成树问题。

K - Kebab House：预处理出 $f_{i,j}$ 表示 $i$ 个位置塞 $\leq j$ 个白日梦，要求最后一个必须塞的方案数，这部分 $O(q^3)$。对于 $n$ 个段，定义 $g_{i,j}$ 表示到第 $i$ 道菜，还要过 $j$ 时刻才能继续做梦。枚举第 $i$ 道菜最后一个白日梦，利用 $f$ 转移，这部分 $O(nqt)$。注意第 $i$ 道菜可以不做梦。

---

U(2013-2014 ACM-ICPC, NEERC, Northern Subregional Contest)

C - Correcting Curiosity：字符串哈希，可以 $O(n^2)$ 处理出按题目所给方法删掉子串 $[l, r]$ 的所有出现位置的哈希值（在段与段之间用特殊字符隔开），两个串都这么处理，哈希值相同的可以作为答案。注意有个串可以为空。（然后我 TM 常数大得不正常，导致我把双哈希的两取模换成一取模一自然溢出才 1.9s 勉强卡过）

H - Heavy Chain Clusterization：经典最小割。

J - J：把所有量存成 $f(X)=\sum_{i\leq 10} a_i X^i$ 的形式，预处理 $s_i = \sum_{j=1}^{N} X_j^i$，然后模拟。

L - Lonely Mountain：有解当且仅当两平面最高高度相同。可以把贡献拆解成若干对三棱柱的交，手推一下 + 排序扫描即可。p