《Fundamentals of Computer Graphics》第十二章 图形数据结构

开篇

  某些数据结构经常在图形应用中出现，也许是因为它们能处理一些底层的基本想法，例如表面、空间和场景结构。这章将探讨图形数据结构中一些不相关的而且很基础的并且最实用的一些类别，这些类别主要有网格结构、空间数据结构、场景图、分块多维数组。
  对于网格来说，我们将讨论一些基础的存储方案，用于存储静态网格或是将网格传输到图形API。我们也会讨论翼边数据结构和与之相关的半边数据结构，这两个数据结构能很好地管理镶嵌细分变化的模型，例如细分或模型简化的时候。尽管这些方法泛化到了任意的多边形网格，但我们还是聚焦于三角形网格这种情况下。
  接下来，将会介绍场景图数据结构，这种数据结构的多种形式在图形应用中无处不在，就是因为它们在管理物体和变换上很有用。所有新的图形API都被设计来支持场景图。
  对于空间数据结构来说，我们会讨论用来组织三维空间中的模型的三种方法，这三种方法有包围体层次结构、层次化空间划分、均匀空间划分，此外还会讨论利用层次化空间划分（BSP树）来移除隐藏表面，相同的方法也被用于不同的目的，包括几何剔除和碰撞检测。
  最后，将会介绍分块多维数组，它一开始被开发是用来提高需要从磁盘换入图形数据的应用的分页性能，而现在，不管数组是否能放入主存储器，这种结构对于机器上的内存局部性至关重要。

三角形网格（Triangle Meshes）

  绝大多数现实世界的模型都是由有着共享顶点的三角形构成的，这些通常被称为三角网格（Triangular Meshes）或不规则三角形网（Triangular Irregular Networks，TINs），有效地处理它们对于图形程序的性能至关重要。网格都是存储在磁盘和内存中的，我们应该最小化存储空间的消耗。当网格在网络中或是从CPU到图形系统传输时，它们会消耗带宽，这通常比存储更宝贵。在那些对网格操作的应用中，除了存储还有绘制它们之外，还有细分、网格编辑、网格压缩等等操作，对于这些操作来说，高效地获取邻接信息至关重要。
  三角形网格通常被用来表示表面，因此网格不是一些相互之间无关的三角形的集合，而是通过共享顶点和共享边相互之间连接的三角形网络，这些三角形一起形成了一个单独的连续表面。这是对网格的一个关键的洞悉，相比于相同数量的无关的三角形的集合，一个网格可以被更加有效率地处理。
  一个三角网格需要的最小信息是一系列三角形以及它们的顶点的位置。在一些情况下，程序需要在顶点、边或面存储额外的信息来支持纹理映射、着色、动画以及其它操作。其中顶点数据是最常见的，每个顶点可以拥有材质参数、纹理坐标、辐照度以及任何在表面上改变的值。这些参数会在每个三角形上被线性插值从而定义了一个在网格的整个表面上的连续函数。然而，存储每条边和每个面的数据有时也很重要。

网格拓扑（Mesh Topology）

  网格是类表面这一想法可以形式化为对网格拓扑的一些约束，也就是不管顶点的位置，对于三角形之间的连接方式的约束。许多算法只会或更容易在网格有可预测的连接性的情况下实现。最简单的也是最有限制的对于网格拓扑的要求是表面应该是流形（Manifold）。一个流形网格应该是“防水的”，也就是没有间隙并把空间分成了表面内部和表面外部。它看起来也像网格上的一个表面。
  流形这个术语来自拓扑的数学领域，大致上讲，一个流形（特别是二维流形）是一个表面，在这个表面上的点和它周围的点只能组成一个比较平坦的表面。接下来让我们看个例子，下方是一张示例图
img

观察一下，很容易发现左边是非流形，因为上下金字塔相接的点与它周围的点可以形成多个表面。许多算法会假设网格是流形，因此应该验证这一属性来避免崩溃或无限循环。这个验证可以归结为通过下面的条件来检查所有边和所有顶点是否都是流形。

  • 每条边都正好被两个三角形共享

  • 每个顶点周围只有一个三角形循环

之前那张示例图就展示了，有太多的三角形循环从而验证失败。下面这张示例图展示了一条边被太多的三角形共享而验证失败。
img

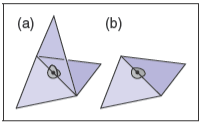
  流形网格很便捷，但是有时应该允许网格有边界。对于一个有着边界的流形我们可以放宽流形网格的要求，放宽后的条件为

  • 每条边被一个或两个三角形使用

  • 每个顶点连接着一个边与边相接的三角形的集合

下方的一张示例图展示了这些条件
img

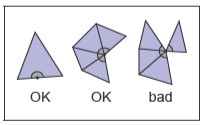
  最后，在许多应用中能够把表面的“前面”或“外面”和表面的“背面”或“里面”区分开来很重要，这被称为表面的朝向（Orientation）。对于一个单独的三角形，我们基于顶点被列出的顺序来定义朝向，正面是按逆时针顺序排列的时候。在一个连通的网格中，如果它的三角形都同意哪一边是正面，那么它的朝向是固定的。
  在一对有一致朝向的三角形中，两个共享的顶点在两个三角形的顶点列表中会以相反的顺序出现，就如下图展示的那样。对于一致朝向重要的是，有些系统会使用顺时针来定义正面而不是逆时针。
img

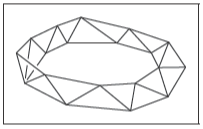
  任何有着非流形边的网格不可能有一致的朝向。对于一个有着边界的流形来说也可能会这样，这种是不可定向的表面，就如下图展示的莫比乌斯带的例子。
img

索引化网格存储（Indexed Mesh Storage）

  一个简单的三角网格如下图所示
img

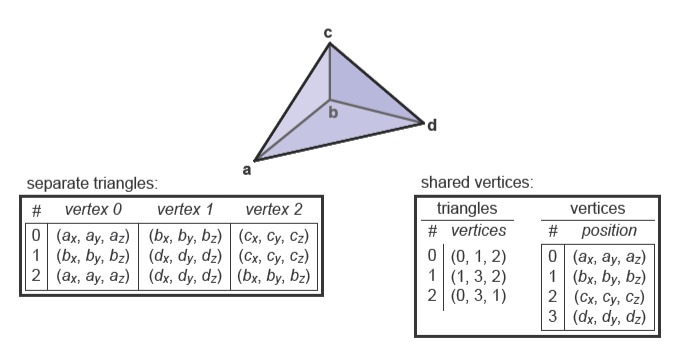
我们可以像下面这样存储每个三角形

Triangle
{
    vector3 vertexPosition[3]
}

不过这样会导致图中的\(\mathbf{b}\)顶点存储三次和其它顶点存储两次。实际上可以采用共享的方式存储四个顶点，这样就有了一个共享顶点的网格（Shared-vertex Mesh）。

Triangle
{
    Vertex v[3]
}

Vertex
{
    vector3 position
    //其它顶点数据
}

要注意的是这里的Vertex v[3]只是顶点对象的引用或指针。在实践中，顶点和三角形通常是存储在数组中的，我们可以使用索引来间接声明三角形的顶点，因此可以使用索引数组来定义网格。

IndexedMesh
{
    int tInd[nt][3]
    vector3 verts[nv]
}

第\(i\)个三角形的第\(k\)个顶点会在顶点数组的第tInd[i][k]个位置，使用这种方法来存储的共享顶点的网格叫索引化三角形网格（Indexed Triangle Mesh）。下方为一张索引化三角形网格的示例图
img

  那么使用共享顶点有没有空间优势呢？如果我们有\(n_v\)个顶点和\(n_t\)个三角形，假设浮点、指针、整数都需要相同的存储空间，那么空间需求有如下：

  • 普通三角网格：每个三角形三个向量也就是\(9n_t\)单位大小。

  • 索引化网格：每个顶点一个向量，每个三角形三个整数，也就是\(3n_v+3n_t\)单位大小。

  根据经验来说，一个大的网格的每个顶点会连接约六个三角形。因为每个三角形连接三个顶点，这意味着三角形数量约为顶点数量的两倍（\(n_t \approx 2 n_v\)）。那么不使用索引化网格需要\(18n_v\)单位，使用只需要\(9n_v\)单位，这样就节省了一半的空间。

三角形条带和三角形扇面（Triangle Strips and Fans）

  索引化网格是最常见的在内存中表示三角形网格的方式，因为它在简单性、便捷性、紧凑性之间达到了良好的平衡。它也通常被用来在网络中和从CPU到图形系统的传输。在一些需要更紧凑性的应用中，三角形顶点的索引可以被更加效率地用三角形条带（Triangle Strip）和三角形扇面（Triangle Fan）来表示。
  一个三角形扇面如下图所示
img

在一个索引化网格中，三角形数组包含\([(0,1,2),(0,2,3),(0,3,4),(0,4,5)]\)，我们存储了12个顶点索引，尽管只有6个不同的顶点。在一个三角形扇面中，所有的三角形共享一个顶点，上图的扇面可以用\([0,1,2,3,4,5]\)来表示，第一个顶点为共享的顶点，它会与后续的每一对相邻的顶点（1-2、2-3等等）创造一个三角形。
  三角形条带是个相似的概念，不过更适用于更大范围的网格。像下图一样，顶点被交替的在上下添加，构成了一个线性条带。
img

上图的条带可以用\([0,1,2,3,4,5,6,7]\)来表达，序列中每三个相邻的顶点（0-1-2、2-1-3等等）创造了一个三角形。对于一个新进入的顶点，最老的顶点会被抛弃，两个剩下的顶点会交换顺序。
  在条带和扇面中，\(n+2\)个顶点就足够描述\(n\)个三角形，相比于标准的索引化网格需要的的\(3n\)个顶点节省了很多。对于长三角形条带来说，可以节省三倍。似乎三角形条带只在条带很长的时候有用，实际上对于相对短的条带来说，已经能获得非常大的提升，存储空间的节省（只对于顶点索引）如下图所示。
img

  因此，即使是一个非结构化的网格，使用一些贪心算法把它们聚集成短条也是值得的。

网格连接性的数据结构（Data Structures for Mesh Connectivity）

  索引化网格、条带、扇面都是静态网格的紧凑且良好的表示，然而它们不容易让网格被修改。为了有效率地编辑网格，更加复杂的数据结构需要快速地回答下方的问题。

  • 给定一个三角形，哪三个三角形与它相邻？

  • 给定一个边，哪两个三角形共享它？

  • 给定一个顶点，哪些面共享它？

  • 给定一个顶点，哪些边共享它？

对于三角形网格、多边形网格和有着孔洞的多边形网格来说，有很多可用的数据结构。在许多应用中，网格会非常大，因此高效地表示至关重要。
  最直接也最臃肿的实现是使用三种类型Vertex、Edge、Triangle存储所有的关系

Triangle
{
    Vertex v[3]
    Edge e[3]
}

Edge
{
    Vertex v[2]
    Triangle t[2]
}

Vertex
{
    Triangle t[]
    Edge e[]
}

这样就能直接回答上面的问题，不过由于这些信息都是相互关联的，因此存储了一些多余的信息。此外，为每个顶点存储连接信息会导致有可变长度的数据结构，这种实现起来效率较低。事实证明，我们可以只存储部分连接信息，在需要的时候可以高效地恢复其它信息。
  固定大小的Edge和Triangle类明显可以更有效率地存储连接信息。事实上，在一个由有着任意数量的边和顶点的多边形组成的多边形网格中，只有边有着固定大小的连接信息，这就导致了有非常多的基于边的传统网格数据结构。但是对于只有三角形的网格来说，在面上存储连接信息也是可以的。
  一个好的网格数据结构应该要足够的紧凑，而且还要能高效地回答所有的邻接查询。这里的高效意味着常时间，也就是找到邻居的时间不应该取决于网格的大小。接下来让我们看看三种数据结构，一个基于三角形，另外两个基于边。

三角形邻接结构（The Triangle-Neighbor Structure）

  我们以之前说的共享顶点的网格为基础，为三角形类增加与它相邻的三个三角形的指针，为顶点类增加任意一个包含它的三角形的指针，这样就实现了一种紧凑的网格数据结构。

Triangle
{
    Triangle nbr[3]
    Vertex v[3]
}

Vertex
{
    Triangle t
}

下方为一张相关的示例图
img

可以发现某个三角形和它的第\(k\)个邻居共享它的第\(k\)和第\((k+1) \; \mathrm{mod} \; 3\)个顶点。我们称这种结构为三角形邻接结构（The Triangle-Neighbor Structure）。从标准的索引化网格开始，我们只需要增加两个数组，一个用来存储每个三角形的三个邻居的索引，另一个用来存储每个顶点的任意一个邻居三角形的索引，就能实现三角形邻接结构。

Mesh
{
    int tInd[nt][3]
    int tNbr[nt][3] //每个三角形的三个邻居的索引
    int vTri[nv] //每个顶点的任意一个邻居三角形的索引
}

这种结构能直接回答前两个问题，对于后两个问题我们得利用现有的信息来回答。回顾之前说的逆时针被列出为正面，以及某个三角形和它的第\(k\)个邻居共享它的第\(k\)和第\((k+1) \; \mathrm{mod} \; 3\)个顶点这两个条件，这个时候就发现了可以以顺时针方向遍历包含相同顶点的三角形，下面给出伪代码

TrianglesOfVertex(v)
{
    t = v.t
    do
    {
        i = find (t.v[i] == v) //搜索得出v是t三角形的第几个顶点
        t = t.nbr[i] //以顺时针方向要遍历的下一个三角形应该是t的第i个邻居三角形
    } while (t != v.t)
}

下方为一张顺时针遍历的示例图
img

这个操作会以常时间找到后续的三角形，然而进行搜索需要额外的分支。我们遇到的问题其实是移动到下一个三角形的时候，就不记得是从哪来了。为了解决这个问题，我们应该存储和边有关的信息。首先，对于任意一个三角形，我们首先应该知道与它的每个边对应的邻居三角形的指针，此外我们还需要知道它的每个边在对应的邻居三角形中的位置，这样就能知道从哪里来。可以通过上方的示例图来说明这一想法，假设现在在\(T_2\)三角形，要前往的下一个三角形是\(T_1\)，通过\(T_2\)边上存储的信息我们可以知道\(\mathbf{p}_2\mathbf{p}_3\)这条边在三角形\(T_1\)中的位置，于是在到达\(T_1\)三角形后，直接访问下一条边也就是\(T_1\)三角形的\(\mathbf{p}_2\mathbf{p}_0\)边上的数据，这样就能直接知道下一个要去的是\(T_0\)三角形。因此有如下的数据结构

Triangle
{
    Edge nbr[3]
    Vertex v[3]
}

Edge
{
    Triangle t//与边对应的邻居三角形
    int i//这条边在对应的邻居三角形中的位置
}

Vertex
{
    Edge e//任意离开顶点的边，如上图的p2p0这种
}

在实践中，Edge中的\(i\)会借用\(t\)两比特位来确保存储空间不变。循环遍历算法为

TrianglesOfVertex(v)
{
    {t, i} = v.e
    do
    {
        {t, i} = t.nbr[i]
        i = (i + 1) mod 3
    } while (t != v.e.t)
}

  三角形邻接结构是非常紧凑的，对于一个只有顶点位置的网格来说，每个顶点要4个数字，每个面要6个数字，每顶点约消耗\(4n_v+6n_t \approx 16n_v\)单位的空间，对于标准的索引化网格来说每顶点要\(9n_v\)。
  在这个部分呈现的三角形邻接结构只对流形网格有用，因为使用的TrianglesOfVertex算法的返回取决于是否回到起点，对于有着边界的流形来说，我们可以引入\(-1\)这样的值，并让边界顶点指向最逆时针的邻居三角形，而不是指向任何任意三角形。

翼边结构（The Winged-Edge Structure）

  一个在边上存储连接信息并被广泛使用的网格数据结构是翼边（winged-edge）数据结构。在一个翼边网格中，每个边会存储它连接的两个顶点的指针，分别为头指针和尾指针。此外还会存储左右两个面的指针和与它相连的四个边的指针，这四个边的指针分为\(\mathrm{ln}\)（Left Next）、\(\mathrm{rn}\)（Right Next）、\(\mathrm{lp}\)（Left Previous）、\(\mathrm{rp}\)（Right Previous）。这里要注意一点，在翼边结构中，从上一个边（Previous）到当前的边再到下一个边（Next）的环绕左右面的回路为逆时针。下方为两张形象的示例图
imgimg

因此类的定义有如下

Edge
{
    Edge lprev, lnext, rprev, rnext
    Vertex head, tail
    Face left, right
}

Face
{
    Edge e//这个面包含的任意一条边
}

Vertex
{
    Edge e//包含这个顶点的任意一条边
}

翼边数据结构支持常时间访问一个面的边和一个顶点的边，有了之前提供的信息，很容易推导出遍历顶点的所有边以及遍历面的所有边的算法为

EdgesOfVertex(v)
{
    e = v.e
    do
    {
        if (e.tail == v)
            e = e.lprev
        else
            e = e.rprev
    } while (e != v.e)
}

EdgesOfFace(f)
{
    e = f.e
    do
    {
        if (e.left == f)
            e = e.lnext
        else
            e = e.rnext
    } while (e != f.e)
}

  这些相同的算法和数据结构可以在不止有三角形的多边形网格中工作，这也是基于边的结构的一个非常重要的优势。和其它的数据结构一样，翼边数据结构可以做一些时间和空间上的衡量。比如，我们可以去除对\(\mathrm{prev}\)的引用，从而节省一定的空间，不过会导致环绕面顺时针遍历或环绕顶点逆时针遍历变难，如果想知道上一个边，那么得顺着下一个边的方向绕一大圈来得到。

半边结构（The Half-Edge Structure）

  翼边数据结构非常优雅，但是在环绕面或顶点遍历时需要时刻检查方向，这就像未被优化的TrianglesOfVertex算法那样。因此，与其在每个边上存储数据，不如在每个半边（half-edge）上存储数据。背后的想法很简单，即把每个边分成朝向相反的一对半边，并分配给共享这个边的两个三角形，要求是每个三角形的半边要有一致的朝向。这样看来每个半边得存储它所属的面和它指向的顶点，除此之外为了方便遍历还得存储它对应的另一个反向半边和它在所属环路中的下一个半边，当然了存储它在环路中的上一个半边也是可以的。下方为一张形象的示例图
img

于是有如下的结构

HEdge
{
    Hedge pair, next
    Vertex v
    Face f
}

Face
{
    HEdge h//这个面包含的任意半边
}

Vertex
{
    HEdge h//指向这个顶点的任意一个半边
}

下面给出使用半边数据结构环绕顶点和面遍历的代码

EdgesOfVertex(v)
{
    h = v.h
    do
    {
        h = h.pair.next
    } while (h != v.h)
}

EdgesOfFace(f)
{
    h = f.h
    do
    {
        h = h.next
    } while (h != f.h)
}

  半边一般都是成对出现的，不过很多的实现不会显式存储\(\mathrm{pair}\)指针。例如在一个基于数组索引的实现中，偶数索引\(i\)的半边与会与索引为\(i+1\)的半边组成一对，奇数索引\(j\)的半边会与索引为\(j-1\)的半边组成一对。就像下图展示的这样
img

  除了这章展示的简单遍历算法外，这三种网格拓扑结构都支持不同类型的“网格手术”操作，比如拆分或合并顶点和边交换，以及添加或删除三角形。

场景图（Scene Graphs）

  一个三角形网格管理着组合成一个物体的所有三角形的集合，但是在图形应用中的另一个普遍的问题是把物体放到期望的位置。就如同我们在第七章看到的那样，摆放物体是通过变换做到的，但是复杂的场景会包含非常多的变换，如果能把这些变换管理好，那么场景就更容易被操作。绝大多数场景都可以使用层次结构来组织，变换可以通过场景图（Scene Graph）按照这种层次来管理。
  为了引出场景图数据结构，我们首先看个铰链摆的例子，下面是与之相关的示例图
img

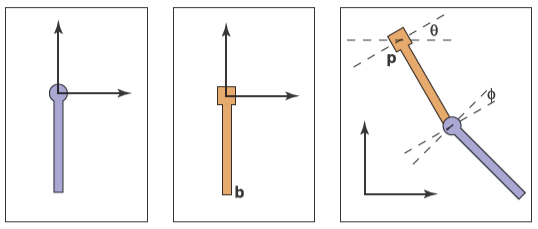
由图可知对于上钟摆的变换\(\mathbf{M}_3\)有

\[\begin{align*} \mathbf{M}_1 &= \mathrm{rotate}(\theta) \\ \mathbf{M}_2 &= \mathrm{translate}(\mathbf{p}) \\ \mathbf{M}_3 &= \mathbf{M}_2\mathbf{M}_1 \end{align*} \]

下钟摆的变换会更复杂，但是我们能利用下钟摆附着在上钟摆的底部也就是局部坐标系中的\(\mathbf{b}\)点这一事实和上下钟摆的旋转角度差也就是上图所示的相对角度\(\phi\)来进行叠加变换。在上钟摆变换前我们先把下钟摆旋转一个相对角度\(\phi\)，然后把下钟摆移动到上钟摆的\(\mathbf{b}\)点位置，接着跟随上钟摆变换即可。使用数学语言来描述下钟摆的变换矩阵\(\mathbf{M}_d\)则为

\[\begin{align*} \mathbf{M}_a &= \mathrm{rotate}(\phi) \\ \mathbf{M}_b &= \mathrm{translate}(\mathbf{b}) \\ \mathbf{M}_c &= \mathbf{M}_b\mathbf{M}_a \\ \mathbf{M}_d &= \mathbf{M}_3\mathbf{M}_c \end{align*} \]

这说明下钟摆的坐标系实际上在跟随上钟摆移动，因此我们能使用一种数据结构来更好地管理这些坐标系的问题，就如同下图展示的这样
img

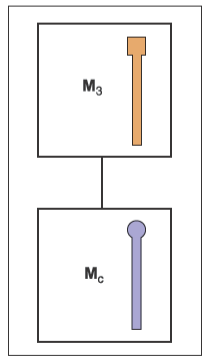
通过利用这种数据结构，我们能得到对于一个物体施加的变换只是从数据结构的根到物体的链条涉及到的所有矩阵的乘积。假设有一个搭载着车辆的渡轮，车可以自由地在甲板上移动，车轮会相对于车移动，于是有如下的数据结构
img

和钟摆一样，每个物体的变换应该是从根到物体的路径涉及到的所有矩阵的乘积，于是有

  • 渡轮的变换使用为\(\mathbf{M}_0\)

  • 车身的变换使用为\(\mathbf{M}_0\mathbf{M}_1\)

  • 左边的轮子使用的变换为\(\mathbf{M}_0\mathbf{M}_1\mathbf{M}_2\)

  • 右边的轮子使用的变换为\(\mathbf{M}_0\mathbf{M}_1\mathbf{M}_3\)

在光栅化中（In rasterization）

  在光栅化中一个高效的实现是矩阵栈（Matrix Stack），这种数据结构被许多的API支持。一个矩阵栈可以通过入栈（Push）和出栈（Pop）来操作，它们实现的是从右侧增加和删除矩阵，比如可以调用

\[\begin{align*} &\mathrm{push}(\mathbf{M}_0) \\ &\mathrm{push}(\mathbf{M}_1) \\ &\mathrm{push}(\mathbf{M}_2) \end{align*} \]

得到活动矩阵\(\mathbf{M}=\mathbf{M}_0\mathbf{M}_1\mathbf{M}_2\)，接着调用\(\mathrm{pop}()\)删除最后一个矩阵，于是活动矩阵变成了\(\mathbf{M}=\mathbf{M}_0\mathbf{M}_1\)。把矩阵栈与场景图结合起来，可以得到使用先序遍历来绘制所有物体的算法
img

场景图有非常多的变种，不过它们都支持上面这种基本的想法。

在光线追踪中（In ray tracing）

  光线追踪的一个优雅性质是，它允许非常自然的变换应用，而不需要改变几何表示。实例化的基本想法是在显示物体前通过变换矩阵来扭曲物体上的所有点，就如下图所示的那样
img

使实体称为“实例”的关键是存储基物体和对应的复合变换矩阵，不过在渲染的时候一般需要显式地构造变换后的几何体。但是在光线追踪中使用实例化有个优势，假如有个基物体，它的一个实例会使用\(\mathbf{M}\)来变换，如果求得的交点为\(\mathbf{P}\)，那么有

\[\mathbf{a} + t \mathbf{b} = \mathbf{P} \]

由于实例是通过矩阵\(\mathbf{M}\)变换的，于是可以在两边乘以矩阵的逆，因此有

\[\mathbf{M}^{-1}\mathbf{a} + t \mathbf{M}^{-1}\mathbf{b} = \mathbf{M}^{-1} \mathbf{P} \]

因为\(\mathbf{M}^{-1} \mathbf{P}\)是基物体上的点，因此我们也可以求被逆变换的光线与基物体的交点。这么做的两个潜在的好处如下：

  1. 基物体可能有更简单的求交流程。

  2. 许多变换后的物体可以共享相同的基物体，因此能节省存储空间。

  这里有个问题要注意，在基物体空间中求交所得到的法线必须被变换到世界空间中，由于实例是用\(\mathbf{M}\)矩阵进行变换的，因此在基物体空间中求交得到的法线\(\mathbf{n}\)得用\((\mathbf{M}^{-1})^\mathrm{T}\)来变换。下面给出实例与光线求交的代码。
img

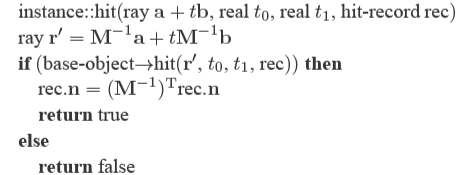
这个代码的一个优雅的地方是参数\(\mathrm{rec}.t\)不需要被修改，因为它和求交所在的空间无关。此外也不需要计算或存储矩阵\(\mathbf{M}\)，只需要它的逆\(\mathbf{M}^{-1}\)。关于上面的代码其实还能有新的认知，那就是不应该限制光线方向\(\mathbf{b}\)为单位向量，如果这样做会导致很多问题，比如无法求出正确的参数\(\mathrm{rec}.t\)。下方为一张在基物体空间中求交和在世界空间中求交的示例图。
img

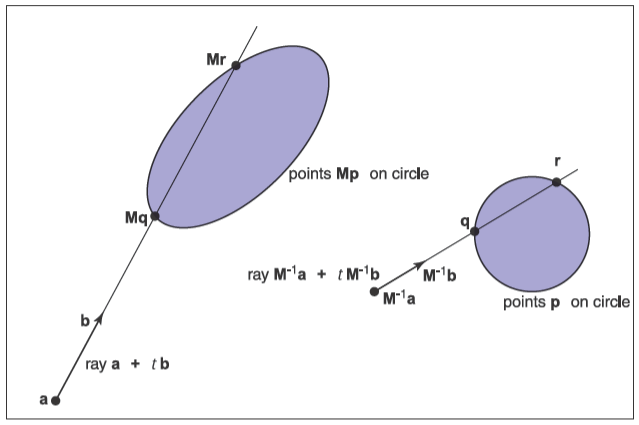
空间数据结构（Spatial Data Structure）

  在很多图形应用中，在特定的区域快速定位几何物体的能力非常重要。光线追踪器需要找到与光线相交的物体，在环境中进行导航的交互式应用需要找到任意视点下可见的物体，游戏以及物理模拟需要检测物体什么时候以及在哪碰撞。这些所有的需求可以通过使用各种各样的空间数据结构来满足，它们可以组织空间中的物体，来让查找更加高效。
  这个部分将讨论三种一般类型的空间数据结构的例子。能将物体组合到一个层次的结构为物体划分结构（Object Partitioning Schemes），虽然物体在这个结构中被分到了不相交的组，但是这些组可能在空间中有重叠。能将空间划分到不相交的区域的结构为空间划分结构（Space Partitionning Schemes），划分可以是规则或不规则的。在规则划分的情况下，空间会被划分为一些形状和大小一致的区域。在不规则划分的情况下，空间会被适应性地划分为一些不规则的区域，在更小区域内会有更多更小的物体。
  讨论这些结构时将使用光线追踪来说明，尽管它们也能被用于视锥体剔除和碰撞检测。在第四章中，当需要检测相交时，我们会遍历空间中的所有物体，这就导致了一个时间复杂度为\(O(N)\)的线性搜索，对于大型场景来说会很慢。和大多数的搜索问题一样，只要我们能预先创建一个有序的数据结构，那么光线与物体的交汇可以使用分而治之的技术，在次线性时间内完成计算。
  下面的部分将详细地讨论这些技术，这些技术主要有包围体层次结构（Bounding Volume Herarchies）、均匀空间划分（Uniform Spatial Subdivision）、二叉空间划分（Binary Space Partition）。下面的一张示例图展示了前两个技术的例子。
img

包围盒（Bounding Boxes）

  对于加速交汇检测的一个关键操作是计算光线是否与包围盒相交，就如下图那样。
img

如果光线不与包围盒相交，那么就不需要检测光线与包围盒中的几何体是否相交。为了建立一个光线与盒相交的算法，我们可以先考虑二维的情况，后续可以推广到三维。我们使用两个水平直线和两个垂直直线来定义二维包围盒，于是有

\[\begin{align*} x &= x_\mathrm{min} \\ x &= x_\mathrm{max} \\ y &= y_\mathrm{min} \\ y &= y_\mathrm{max} \\ \end{align*} \]

那么被这个包围盒包围的点为

\[(x,y) \in [x_\mathrm{min},x_\mathrm{max}] \times [y_\mathrm{min},y_\mathrm{max}] \]

由于只要确定是否相交而不是求交点，我们能采用一个更快的方法。首先先计算光线与水平直线的两个交点的参数\(t\)，于是有

\[t_\mathrm{xmin} = (x_\mathrm{min}-x_e)/x_d \]

\[t_\mathrm{xmax} = (x_\mathrm{max}-x_e)/x_d \]

计算出来参数后，我们能得到一个区间\([t_\mathrm{xmin},t_\mathrm{xmax}]\)。对于垂直直线的情况，我们如法炮制，得到另一个区间\([t_\mathrm{ymin},t_\mathrm{ymax}]\)。接下来需要判断这两个区间是否重叠，如果重叠，那么意味着光线上有点在包围盒内，也就意味着光线和包围盒相交，反之则不相交。因此算法的伪代码为

t_xmin = (x_min - x_e) / x_d
t_xmax = (x_max - x_e) / x_d
t_ymin = (y_min - y_e) / y_d
t_ymax = (y_max - y_e) / y_d

if (t_xmin > t_ymax) or (t_ymin > t_xmax)
    return false
else
    return true

这里有些地方要注意，首先\(x_d\)或\(y_d\)可能是负的。如果\(x_d\)是负的，那么得交换下顺序，于是有

if (x_d >= 0)
    t_xmin = (x_min - x_e) / x_d
    t_xmax = (x_max - x_e) / x_d
else
    t_xmin = (x_max - x_e) / x_d
    t_xmax = (x_min - x_e) / x_d

其次还要注意\(x_d\)或\(y_d\)为\(0\)的情况，回顾第一章提到的的IEEE浮点数模型，里面提到对于任意正实数\(a\)有

\[+a/0 = +\infty \\ -a/0 = -\infty \]

当\(x_d=0\)时，有

\[t_\mathrm{xmin} = \frac{x_\mathrm{min}-x_e}{0} \]

\[t_\mathrm{xmax} = \frac{x_\mathrm{max}-x_e}{0} \]

于是有以下三种情况需要考虑

  1. \(x_e \leq x_\mathrm{min}\)

  2. \(x_\mathrm{min} < x_e < x_\mathrm{max}\)

  3. \(x_\mathrm{max} \leq x_e\)

对于第一种情况，我们能得到区间\((t_\mathrm{xmin},t_\mathrm{xmax})=(\infty,\infty)\)，这个区间不会与任意的区间重叠，因此不会相交，这是我们期望的一个结果。对于第二种情况我们能得到区间\((t_\mathrm{xmin},t_\mathrm{xmax})=(-\infty,\infty)\)，这个区间会与任意区间重叠，因此会有相交，这也是我们期望的一个结果。第三种情况和第一种一样不会有相交。因此对于以上这些情况我们能信任IEEE浮点数模型，不过还有最后一个问题要注意，假如我们使用

if (x_d >= 0)
    t_xmin = (x_min - x_e) / x_d
    t_xmax = (x_max - x_e) / x_d
else
    t_xmin = (x_max - x_e) / x_d
    t_xmax = (x_min - x_e) / x_d

当\(x_d=-0\)时又会出问题，解决方法也很简单，就是使用\(x_d\)的倒数进行计算，因此有

a = 1 / x_d
if (a >= 0)
    t_xmin = a*(x_min - x_e)
    t_xmax = a*(x_max - x_e)
else
    t_xmin = a*(x_max - x_e)
    t_xmax = a*(x_min - x_e)

层次包围盒（Hierarchical Bounding Boxes）

  层次包围盒的基本想法是使用轴对齐的包围盒来包围所有物体。虽然光线与包围盒的相交计算有开销，但是一旦光线未命中包围盒，那么就能减少大量的相交检测。使用更大的包围盒来包围小的包围盒就形成了层次结构，一张相关的示例图如下
img

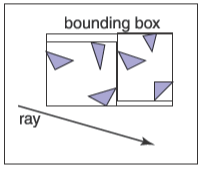
而与之相关的一张可能的数据结构的示例图如下
img

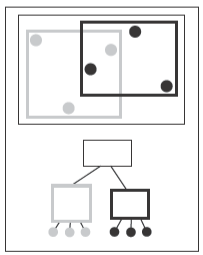
为了计算光线与物体的交点，我们必须遍历树中的节点，于是有如下的算法
img

观察这个算法你会发现子树之间没有几何顺序，也就是说光线可能会同时击中两个子树。这是因为包围盒只会保证包围在它层次之下的所有物体，而不会保证包围盒之间在空间中不重叠，就如之前所展示的数据结构的示例图那样。这就导致了这种几何搜索会比传统的二叉搜索要复杂，对于这种情况你可能想到了一些可能的优化方法，等我们有一个完整的层次算法时再来想它。
  如果我们限制树为二叉的并且要求树中的每个节点都有一个包围盒，那么遍历代码可以自然地展开。除此之外，假设每个叶子节点包含一个图元，每个非叶子节点包含一个或两个子树。
  bvh-node类应该是表面类的子类，因此它应该实现surface::hit。它包含的数据应该很简单，于是有
img

遍历的代码可以使用递归来实现，因此有
img

  有许多方式来建立包围体层次结构的树。如果能创建一个大致平衡的二叉树，并让兄弟子树的包围盒不重叠太多，那么将会很便捷。实现这个的一个启发式方法是在划分表面到两个子列表前，先沿着一条轴排序。如果我们使用整数来定义这些轴\(x=0\)、\(y=1\)、\(z=2\)那么有
img

在排序的时候小心地选择轴就能提高树的质量。有个方法是通过让两个子树的包围盒的总体积最小化来选择轴。与依次循环使用坐标轴相比，这种方法对于有着分布均匀的小物体的场景来说，不会带来太大差别，但是对于那些杂乱的场景来说，它带来的提升可能很大。通过只进行划分而不是完整的排序，上述的代码也可以变得更加地有效率。
  另一个可能更好的建立树的方法是让子树包含差不多大小的空间，而不是包含相同数量的物体。为了做到这件事，我们基于空间来划分表，因此有如下的代码
img

虽然这会导致一个不平衡的树，但是它允许更加轻松地遍历空白空间，此外还更容易被建立，因为划分比排序的开销要低。

均匀空间划分（Uniform Spatial Subdivision）

  另一个能减少交汇检测策略是划分空间，这和层次包围体有很大的不同。在层次包围体中，每个物体属于兄弟节点的其中一个。而在空间划分中，每个在空间中的点只属于一个节点。在均匀空间划分中，场景被划分到了轴对齐的盒中。这些盒都有相同的大小，尽管它们不一定要是立方体。下图展示了光线遍历这些盒的例子
img

当一个物体被击中时，遍历会终止。网格本身应该是表面类的子类，而且应该被实现为指向表面的指针的三维数组。对于空的格子来说，这些指针就是NULL。对于有一个物体的格子，指针会指向那个物体。对于有着更多物体的格子，指针可以指向一个列表或其它网格，又或者是其它的数据结构，比如层次包围体。
  遍历是以增量方式完成的，为了了解是怎么具体完成的，我们可以先考虑二维的情况，假设光线方向的分量都为正且光线从网格外出发，网格有\(n_x \times n_y\)个格子且被点\((x_\mathrm{min},y_\mathrm{min})\)和点\((x_\mathrm{max},y_\mathrm{max})\)包围。
  我们的第一个任务就是找到第一个被光线\(\mathbf{e}+t\mathbf{d}\)击中的格子的索引\((i,j)\)，接着需要以正确的顺序遍历格子。因此算法的关键是找到开始的格子\((i,j)\)然后决定是要增加\(i\)还是\(j\)。这里要注意，当检查光线与格子包含的物体的是否相交时，参数\(t\)会被限制在格子内，就如下图展示的那样。
img

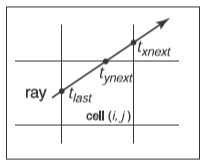
绝大多数的实现都会让“指向表面的指针”作为三维数组的类型，为了改善遍历的局部性，三维数组可以被展平成一维数组，这个将在后续讨论。

轴对齐的二叉空间划分（Axis-Aligned Binary Space Partitioning）

  我们也可以使用层次数据结构来划分空间，例如二叉空间划分树（Binary Space Partitioning Tree，BSP tree）。这和后续的用于可见度排序的BSP树相似，对于光线相交的情况，一般会使用与轴对齐的平面来划分，而不是与多边形对齐的平面。
  在这个结构中的节点包含一个切割平面以及一个左子树和右子树，每个子树包含在切割平面一边的所有物体，穿过平面的物体会被存储在两个子树中。如果我们假设切割平面平行于\(yz\)平面于\(x=D\)，那么节点类应该是
img

后续可以推广到\(y\)和\(z\)切割平面的情况。相交的代码可以使用递归的方式来实现，而且应该考虑如下图所示的四种情况
img

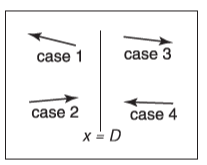
我们让光线从参数\(t_0\)开始传播，于是有

\[\mathbf{p} = \mathbf{a} + t_0 \mathbf{b} \]

下面为四种要考虑的情况

  1. 光线只与左子树交互，我们不需要检测其与切割平面的相交。这只在\(x_p<D\)且\(x_b<0\)时发生。

  2. 测试与左子树的物体相交后发现没有击中，接着测试与右子树物体的相交。我们需要找到在\(x=D\)时的光线参数，把求交范围限制在子树内部。这种情况只在\(x_p<D\)且\(x_b>0\)时发生。

  3. 这种情况和第一种情况类似，只会在\(x_p>D\)且\(x_b>0\)时发生。

  4. 这种情况和第二种情况类似，只会在\(x_p>D\)且\(x_b<0\)时发生。

因此，处理这些情况的代码为
img

上述的代码非常简洁，然而为了开始，我们需要击中根节点对象的包围盒，来初始化遍历。此外我们需要解决的一个问题是切割平面可能会沿着任意轴，对此我们可以在bsp-node类中增加一个整数成员来指定轴，如果点允许索引操作，那么上方的代码只需要一些小的修改，例如把

\[x_p = x_a + t_0 x_b \]

修改成

\[u_p=a[\mathrm{axis}]+t_0b[\mathrm{axis}] \]

这会导致一些额外的数组索引，但是不会产生更多的分支。
  虽然一个bsp-node的处理比一个bvh-node的处理要快，但是一个表面可能会出现在多个子树中，这意味着会有更多的节点，带来了潜在的更高的内存使用。和构建BVH树相似，我们可以选择一个轴在一次循环中进行分割，每次可以分成一半或者采用其它更精细的方式。

用于可见度的BSP树（BSP Tree for Visibility）

  空间数据结构可以解决的另一个问题是，当视点变化时确定场景中的物体的可见度顺序。如果我们要为一个由平面多边形组成的场景生成图像，那么可以使用一种二叉空间划分结构，这和上个部分的轴对齐的二叉空间划分结构有点类似，区别是对于可见度排序来说，不会使用轴对齐的切割平面，而是与几何体共面的平面。这样就有了一个优雅的BSP树算法，用于从前往后排序表面。对于BSP树的一个关键是使用预处理创建一个对任意视点都有用的数据结构。因此，在视点变化时，可以使用相同的数据结构而不需要进行修改。

BSP树算法的概述（Overview of BSP Tree Algorithm）

  BSP树算法是画家算法（Painter's Algorithm）的一个例子，画家算法会从后往前绘制每个物体，就如下图所展示的那样
img

它可以像下面这样被简单地实现
img

在第一步也就是排序，我们遇到的第一个问题是物体之间并不总是有明确的顺序关系，比如下图所展示的循环遮蔽的情况。
img

  BSP树算法只有在构成场景的任意多边形不穿过场景中的其它多边形定义的平面时才有用，不过这个限制可以被另一个预处理步骤放宽。对于接下来的讨论，我们只考虑三角形这一情况。
  BSP树的基本想法可以使用两个三角形\(T_1\)和\(T_2\)来说明，首先得回顾隐式平面方程\(f(\mathbf{p})\)，对于位于平面不同侧的点来说，函数值有不同的符号，于是我们可以利用\(T_1\)三角形定义的平面的隐式方程\(f_1(\mathbf{p})\)。假设\(T_2\)三角形的所有顶点在\(f_1(\mathbf{p})<0\)这一侧，那么对于任意视点\(\mathbf{e}\)有如下的绘制算法。
img

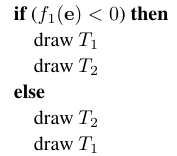
这么做的原因很简单，当视点\(\mathbf{e}\)和\(T_2\)三角形同侧时，不管视点\(\mathbf{e}\)在哪，在渲染出来的图像中，\(T_1\)三角形永远都不会部分覆盖\(T_2\)三角形。反之，则\(T_2\)三角形永远都不会部分覆盖\(T_1\)三角形，下方是一张形象的示例图
img

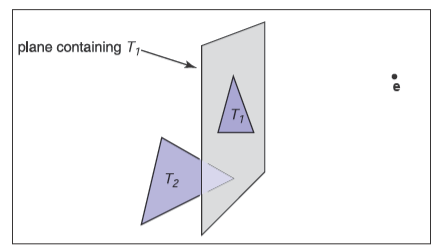
由此，我们能构建一个以\(T_1\)为根的二叉树数据结构，树的负分支包含那些顶点\(f_i(\mathbf{p})<0\)的三角形，树的正分支包含那些顶点\(f_i(p)>0\)的三角形，接着我们就能以如下顺序进行绘制
img

对于任意的视点\(\mathbf{e}\)来说，上述代码都能正确执行。唯一的问题是当三角形穿过了又其它三角形定义的平面时，代码就不能正确工作。在这种情况下有两个顶点会在一侧，剩下一个顶点会在另一侧，因此我们要把这种三角形“切割”成更小的三角形。

树的构建（Building the Tree）

  如果数据集中没有三角形穿过其它三角形定义的平面，那么我们能用如下的方法来构造树。
img

我们唯一要解决的是下图所示的三角形穿过划分平面的情况。
img

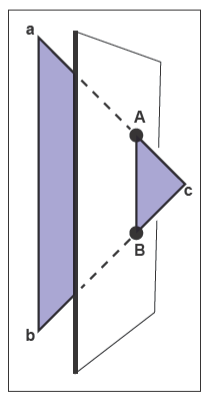
在上图这种情况中，我们首先得求出交点\(\mathbf{A}\)和\(\mathbf{B}\)，接着就能得到三个小三角形，分别为

\[\begin{align*} T_1 = (\mathbf{a},\mathbf{b},\mathbf{A})\\ T_2 = (\mathbf{b},\mathbf{B},\mathbf{A})\\ T_3 = (\mathbf{A},\mathbf{B},\mathbf{c}) \end{align*} \]

这里要注意一点，小三角形顶点的顺序很重要，因为要保持和大三角形相同的朝向。假设\(f(\mathbf{c})<0\)，那么把这三个三角形添加到两个子树的代码为
img

此外我们还要注意精度问题，比如之前所展示的例子的\(\mathbf{c}\)点有可能离分割平面很近，这就导致了切割出来的其中一个三角形非常小，因此我们要检测这种情况而且最好不做处理，于是有如下的代码
img

切割三角形（Cutting Triangles）

  对于切割三角形来说，有不同的情况要考虑，我们应该利用BSP树的构建是个预处理过程，最高效率不是关键，写出清晰且紧凑的代码。一个好的技巧是通过交换顶点，确保\(\mathbf{c}\)顶点总是单独在另一边的那个顶点。这么处理后就只需要处理一种情况，于是有如下的代码
img

当顶点被交换的时候，我们应该执行两次交换来确保顶点有逆时针顺序。这里要注意，当被切割的三角形的其中一个顶点正好在平面上时，会生成一个有\(0\)面积的三角形，不过我们可以忽略这种情况，因为风险不是很大，光栅化代码会帮我们处理这种情况。如果实在觉得不行，也可以检测面积，防止\(0\)面积的三角形被加入树。
  为了计算\(\mathbf{A}\)和\(\mathbf{B}\)，我们有参数直线

\[\mathbf{p}(t) = \mathbf{a} + t(\mathbf{c-a}) \]

与平面\(\mathbf{n} \cdot \mathbf{p} + D = 0\)求交则有

\[\mathbf{n} \cdot (\mathbf{a} + t(\mathbf{c-a})) + D = 0 \]

解得

\[t = - \frac{\mathbf{n} \cdot \mathbf{a} + D}{\mathbf{n} \cdot (\mathbf{c-a})} \]

令求得的参数为\(t_A\)，那么求得\(\mathbf{A}\)为

\[\mathbf{A} = \mathbf{a} + t_A (\mathbf{c-a}) \]

我们可以使用相同的方法来计算\(\mathbf{B}\)。

树的优化（Optimizing the Tree）

  树的构建只是个预处理过程，因此效率不是太重要，而遍历BSP树所花费的时间会和树中的节点数量成比。每个节点对应着一个三角形，节点的数量会取决于三角形被添加到树中的顺序，就比如下图这个例子
img

如果让图中的大三角形为根节点，那么树中会有两个节点。但是如果让小三角形为根节点，那么会有更多的节点，这是因为大三角形被切割成了更多的小三角形。
  要找到最好的顺序非常难，对于\(N\)个三角形来说就有\(N!\)个可能，尝试每种可能是不实际的。有一个替代方法是，进行随机排列选出最好的那一个。

分块多维数组（Tiling Multidimensional Arrays）

  高效地利用内存层次结构对于为现代架构设计算法来说，是至关重要的任务。确保多维数组的数据有好的存储布局是通过分块（Tiling）或分砖（Bricking）做到的。一个传统的二维数组的存储是通过使用一维数组和索引机制做到的。例如一个\(N_x \times N_y\)的数组会存储在一个长度为\(N_xN_y\)的一维数组中，二维索引\((x,y)\)会使用下方的公式映射到一维索引。

\[\mathrm{index} = x + N_xy \]

下图展示了在这种情况下，内存布局的一个示例。
img

从图中我们能看出一个问题，二维位置相邻的元素在实际的一维空间中可能不会相邻。如果\(N_x\)较大，那么会有较差的内存局部性。标准的解决方案是用分块（Tile）让行和列的内存局部性更加均匀。一个使用\(2 \times 2\)分块的例子如下所示
img

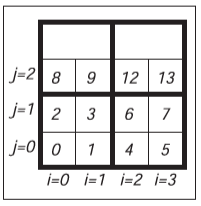
在后续的部分，我们将会讨论使用这种数组的索引的细节。在那之后还有更复杂的例子，即在三维数组上使用两级分块。
  一个关键的问题是分块要有多大。在实践中，分块的大小应该与机器的内存单元大小接近。例如，如果我们在一台有着128字节大小的缓存行的机器上使用16位数据，那么8x8的分块正好能装进一个缓存行。如果使用的是32位的浮点数，一个缓存行能容纳32个元素，5x5的分块显得稍微小了点，而6x6的分块又稍微显得大了点。由于还有更大粒度的内存单位，比如内存页，因此可以采用有着类似逻辑的分层分块方法。

对于二维数组的一级分块（One-Level Tiling for 2D Arrays）

  假设我们使用\(n \times n\)的分块来分解\(N_x \times N_y\)的数组，下图为一张示例图
img

需要的分块的数量为

\[\begin{align*} B_x &= N_x / n \\ B_y &= N_y /n \end{align*} \]

在这里我们假设\(N_x\)和\(N_y\)能被\(n\)整除，否则数组需要被填充（Padding）。比如，如果\(N_x=15\)且\(n=4\)，那么\(N_x\)应该被修改为16。为了得出这种数组的索引方法，我们首先得计算分块的索引\((b_x,b_y)\)

\[b_x = x \div n \]

\[b_y = y \div n \]

这里的\(\div\)表示的是整数除法，比如\(12 \div 5 = 2\)。求得分块的索引后，那么某个分块中的第一个元素的索引为

\[\mathrm{index} = n^2 (B_x b_y + b_x) \]

接着我们需要求元素在分块内部的索引\((x^\prime,y^\prime)\)，实际上就是取模运算，即

\[x^\prime = x \; \mathrm{mod} \; n \]

\[y^\prime = y \; \mathrm{mod} \; n \]

求出分块内部的索引后，那么元素相对于分块内第一个元素的索引的偏移\(\mathrm{offset}\)为

\[\mathrm{offset} = y^\prime n + x^\prime \]

因此把元素的二维索引映射到一维索引的公式为

\[\begin{align*} \mathrm{index} &= n^2 (B_x b_y + b_x) + y^\prime n + x^\prime \\ &=n^2((N_x \div n)(y \div n)+x \div n) +(y \; \mathrm{mod} \; n)n+(x \; \mathrm{mod} \; n) \end{align*} \]

这个表达式包含很多乘法、除法、取模，在某些处理器上的开销很昂贵。当\(n\)是\(2\)的幂时，这些操作可以被转化为移位和位逻辑操作。然而正如之前提到的那样，\(n\)的大小不总会是\(2\)的幂。有些乘法运算可以被转化为移位或加法操作，但是除法和取模则更棘手。索引虽然可以通过增量的方法来计算，但是这需要维护计数器，从而带来大量的比较操作，而且会导致分支预测性能不佳。
  实际上有一种简单的解决方法，索引表达式可以被写为

\[\mathrm{index} = F_x(x) + F_y(y) \]

而

\[\begin{align*} F_x(x)&=n^2(x \div n)+(x \; \mathrm{mod} \; n) \\ F_y(y)&=n^2(N_x \div n)(y \div n) + (y \; \mathrm{mod} \; n)n \end{align*} \]

我们可以预计算\(F_x(x)\)和\(F_y(y)\)的值并制成表，接着在使用的时候让\(x\)和\(y\)作为索引来找到对应的值。即使是数据规模非常大的情况下，表的总大小也可以被放进处理器的一级数据缓存。

三维数组的二级分块的例子（Example: Two-Level Tiling for 3D Arrays）

  有效利用\(\mathbf{TLB}\)（Translation Lookaside Buffer，快表）也是算法性能中的一个至关重要的因素。可以使用类似的方法来提高三维数组的\(\mathbf{TLB}\)命中率：先将数组划分为\(n \times n \times n\)的小单元，再将这些小单元组合成\(m \times m \times m\)的大块。比如一个\(40 \times 20 \times 19\)的三维数据体可以被划分为\(4 \times 2 \times 2\)的宏块，每个宏块由\(2 \times 2 \times 2\)的小块组成，每个小块又包含\(5 \times 5 \times 5\)的单元。在这里对应的参数为\(m=2\)，\(n=5\)。由于\(19\)不能被\(mn=10\)整除，因此需要对数组进行一级填充。从经验来看，对于16位数据集，较为合适的宏块大小为\(m=5\)。而对于浮点数据集，较合适的宏块大小为\(m=6\)。
  对于任意\((x,y,z)\)，索引计算的表达式为

\[\begin{align*} \mathrm{index} = &((x \div n)\div m)n^3m^3((N_z \div n)\div m)((N_y \div n) \div m) \\ &+((y \div n) \div m)n^3m^3((N_z \div n) \div m) \\ &+((z \div n) \div m)n^3m^3 \\ &+((x \div n) \; \mathrm{mod} \; m) n^3 m^2 \\ &+((y \div n) \; \mathrm{mod} \; m)n^3 m \\ &+((z \div n) \; \mathrm{mod} \; m)n^3 \\ &+(x \; \mathrm{mod} \; n)n^2 \\ &+(y \; \mathrm{mod} \; n)n \\ &+(z \; \mathrm{mod} \; n) \end{align*} \]

其中\(N_x\)、\(N_y\)、\(N_z\)分别为数据集的大小。
  与之前的二维数组的一级分块类似，表达式可以被写为

\[\mathrm{index} = F_x(x)+F_y(y)+F_z(z) \]

而

\[\begin{align*} F_x(x) = &((x \div n)\div m)n^3m^3((N_z \div n)\div m)((N_y \div n) \div m)\\ &+((x \div n) \; \mathrm{mod} \; m) n^3 m^2 \\ &+(x \; \mathrm{mod} \; n)n^2 \\ F_y(y) = &((y \div n) \div m)n^3m^3((N_z \div n) \div m) \\ &+((y \div n) \; \mathrm{mod} \; m)n^3 m \\ &+(y \; \mathrm{mod} \; n)n \\ F_z(z) = &((z \div n) \div m)n^3m^3 \\ &+((z \div n) \; \mathrm{mod} \; m)n^3 \\ &+(z \; \mathrm{mod} \; n) \end{align*} \]

posted @ 2025-09-07 23:39  TiredInkRaven  阅读(41)  评论(0)    收藏  举报