《Fundamentals of Computer Graphics》第六章 线性代数

开篇

  也许，图形程序中最通用的的工具就是那些用来变换（Transform）点和向量的矩阵，这章主要讲的是线性代数的基础知识。

行列式（Determinants）

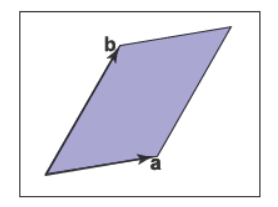
  我们一般可能会想行列式会在线性方程组的解中出现，不过可以先以向量相乘的方式来思考行列式。对于二维向量来说，行列式\(|\mathbf{a}\mathbf{b}|\)是由向量\(\mathbf{a}\)和向量\(\mathbf{b}\)围成的平行四边形的面积决定的，如下图所示。

不过这个面积是有符号的，如果是右手的那么为正，反之则为负，因此我们可以得到\(|\mathbf{a}\mathbf{b}|=-|\mathbf{b}\mathbf{a}|\)。这里的“右手的”可以理解为当逆时针旋转第一个向量时，它和第二个向量的夹角会变小。在三维中，行列式要用到三个向量，对于三个向量\(\mathbf{a}\)、\(\mathbf{b}\)、\(\mathbf{c}\)来说，行列式\(|\mathbf{a}\mathbf{b}\mathbf{c}|\)是由这三个向量围成的平行六面体的有符号容积决定的。
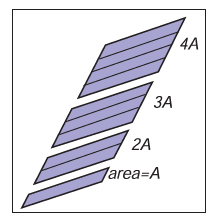
  为了计算二阶行列式，我们首先可以了解下它的相关性质，缩放某个向量会缩放平行四边形的面积，因此可以得到

\[|(k\mathbf{a})\mathbf{b}|=|\mathbf{a}(k\mathbf{b})|=k|\mathbf{a}\mathbf{b}| \]

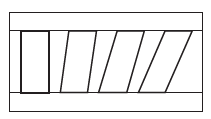
剪切平行四边形不会改变它的面积，因此

\[|(\mathbf{a}+k\mathbf{b})\mathbf{b}|=|\mathbf{a}(\mathbf{b}+k\mathbf{a})|=|\mathbf{a}\mathbf{b}| \]

假设我们用笛卡尔坐标来表示\(\mathbf{a}\)和\(\mathbf{b}\)，行列式\(|\mathbf{ab}|\)可以如下计算

\[\begin{align*} |\mathbf{ab}| &= |(x_a\mathbf{x}+y_a\mathbf{y})(x_b\mathbf{x}+y_b\mathbf{y})| \\ &=x_ax_b|\mathbf{xx}|+x_ay_b|\mathbf{xy}|+y_ax_b|\mathbf{yx}|+y_ay_b|\mathbf{yy}| \\ &=x_ax_b(0)+x_ay_b(+1)+y_ax_b(-1)+y_ay_b(0)\\ &=x_ay_b-y_ax_b \end{align*} \]

因此在三维中

\[\begin{align*} |\mathbf{abc}| &= |(x_a\mathbf{x}+y_a\mathbf{y}+z_a\mathbf{z})(x_b\mathbf{x}+y_b\mathbf{y}+z_b\mathbf{z})(x_c\mathbf{x}+y_c\mathbf{y}+z_c\mathbf{z})| \\ &=x_ay_bz_c-x_az_by_c-y_ax_bz_c+y_az_bx_c+z_ax_by_c-z_ay_bx_c \end{align*} \]

矩阵（Matrices）

  一个矩阵是遵循某些算术规则的数值元素数组，一个两行三列的矩阵可以如下所示

\[\begin{bmatrix} 1.7 & -1.2 & 4.2 \\ 3.0 & 4.5 & -7.2 \end{bmatrix} \]

矩阵算数（Matrix Arithmetic）

对于给定的矩阵，乘以一个常数可以得到

\[2 \begin{bmatrix}1 & -4 \\ 3 & 2 \end{bmatrix} = \begin{bmatrix} 2 & -8 \\ 6 & 4 \end{bmatrix} \]

两个矩阵求和可以得到

\[\begin{bmatrix} 1 & -4 \\ 3 & 2 \end{bmatrix} + \begin{bmatrix} 2 & 2 \\ 2 & 2 \end{bmatrix} = \begin{bmatrix} 3 & -2 \\ 5 & 4 \end{bmatrix} \]

两个矩阵相乘可以得到

\[\begin{bmatrix} a_{11} & \cdots & a_{1m} \\ \vdots && \vdots \\ \boxed{a_{i1}} & \boxed{\cdots} & \boxed{a_{im}} \\ \vdots && \vdots \\ a_{r1} & \cdots & a_{rm} \end{bmatrix} \begin{bmatrix} b_{11} & \cdots & \boxed{b_{1j}} & \cdots & b_{1c} \\ \vdots && \boxed{\vdots} && \vdots \\ b_{m1} & \cdots & \boxed{b_{mj}} & \cdots & n_{mc} \end{bmatrix} = \begin{bmatrix} p_{11} & \cdots & p_{1j} & \cdots & p_{1c} \\ \vdots && \vdots && \vdots \\ p_{i1} & \cdots & \boxed{p_{ij}} & \cdots & p_{ic} \\ \vdots && \vdots && \vdots \\ p_{r1} & \cdots & p_{rj} & \cdots & p_{rc} \end{bmatrix} \]

\[p_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots+a_{im}b_{mj} \]

下面是个矩阵相乘的例子

\[\begin{bmatrix} 0 & 1 \\ 2 & 3 \\ 4 & 5 \end{bmatrix} \begin{bmatrix} 6 & 7 & 8 & 9 \\ 0 & 1 & 2 & 3 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 2 & 3 \\ 12 & 17 & 22 & 27 \\ 24 & 33 & 42 &51 \end{bmatrix} \]

要注意的是矩阵相乘不服从交换律，因此

\[\mathbf{A}\mathbf{B} \neq \mathbf{B}\mathbf{A} \]

而且如果已知\(\mathbf{A}\mathbf{B} = \mathbf{A}\mathbf{C}\)，矩阵\(\mathbf{B}\)有可能不会等于矩阵\(\mathbf{C}\)。不过幸运的是矩阵相乘服从结合律和分配律，因此

\[\begin{align*} \mathbf{(AB)C}&=\mathbf{A(BC)}\\ \mathbf{A(B+C)}&=\mathbf{AB+AC}\\ \mathbf{(A+B)C}&=\mathbf{AC+BC} \end{align*} \]

矩阵中的操作（Operation on Matrices）

  对于一个矩阵来说我们可能会考虑到它的逆，就像对于实数\(x\)来说的\(1/x\)一样。实数\(x\)乘以它的逆\(1/x\)为实数\(1\)，那么矩阵\(\mathbf{A}\)乘以它的逆\(\mathbf{A}^{-1}\)，应该等于“矩阵\(1\)”。这种矩阵只在方块矩阵中出现，它被称为单位矩阵（Identity Matrix）。这个矩阵的对角线上的元素为\(1\)其它元素为\(0\)，比如

\[\mathbf{I} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]

因此\(\mathbf{A}\mathbf{A}^{-1}=\mathbf{I}\)，下面是个矩阵求逆的例子

\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}^{-1} = \begin{bmatrix} -2.0 & 1.0 \\ 1.5 & -0.5 \end{bmatrix} \]

因为

\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \begin{bmatrix} -2.0 & 1.0 \\ 1.5 & -0.5 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \]

此外矩阵的逆还有如下性质

\[(\mathbf{AB})^{-1}=\mathbf{B^{-1}A^{-1}} \]

一个矩阵的转置\(\mathbf{A^{\mathrm{T}}}\)和\(\mathbf{A}\)有相同的数字，不过是\(\mathbf{A}\)行列交换后的结果，因此

\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix}^{\mathrm{T}} = \begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 &6 \end{bmatrix} \]

矩阵的转置有如下性质

\[\mathbf{(AB)}^{\mathrm{T}}=\mathbf{B^{\mathrm{T}}A^{\mathrm{T}}} \]

矩阵的行列式就是把矩阵的括号替换成竖线，有如下性质

\[|\mathbf{AB}|=|\mathbf{A}||\mathbf{B}| \]

\[|\mathbf{A}^{-1}|=\frac{1}{|\mathbf{A}|} \]

\[|\mathbf{A}^{\mathrm{T}}|=|\mathbf{A}| \]

使用矩阵操作向量（Vector Operations in Matrix Form）

  有时候我们有可能想旋转一个二维向量\(\mathbf{a}=(x_a,y_a)90°\)到\(\mathbf{a}^{\prime}=(-y_a,x_a)\)，可以使用一个\(2 \times 2\)的矩阵乘以一个\(2 \times 1\)的矩阵来表示这一变换，这个\(2 \times 1\)的矩阵叫做列向量（Column Vector），因此

\[\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} x_a \\ y_a \end{bmatrix} = \begin{bmatrix} -y_a \\ x_a \end{bmatrix} \]

我们也可以使用行向量和上式的矩阵的转置相乘来得到这一变换

\[\begin{bmatrix} x_a & y_a \end{bmatrix} \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} = \begin{bmatrix} -y_a & x_a \end{bmatrix} \]

此外我们也可以用矩阵相乘来得到向量点乘的结果，假设有列向量\(\mathbf{a}\)和\(\mathbf{b}\)，可以得到

\[\mathbf{a} \cdot \mathbf{b} = \mathbf{a}^{\mathrm{T}} \mathbf{b} \]

以三维向量的点积为例，可以得到

\[\begin{bmatrix} x_a & y_a & z_a \end{bmatrix} \begin{bmatrix} x_b \\ y_b \\ z_b \end{bmatrix} = \begin{bmatrix} x_ax_b + y_ay_b + z_az_b \end{bmatrix} \]

对于\(\mathbf{ab^{\mathrm{T}}}\)的情况我们也可以了解下，这个时候

\[\begin{bmatrix} x_a \\ y_a \\ z_a \end{bmatrix} \begin{bmatrix} x_b & y_b & z_b \end{bmatrix} = \begin{bmatrix} x_ax_b & x_ay_b & x_az_b \\ y_ax_b & y_ay_b & y_az_b \\ z_ax_b & z_ay_b & z_az_b \end{bmatrix} \]

其实我们还可以从不同的角度看待矩阵变换向量和点，接下来以\(3 \times 3\)的矩阵变换为例，对于\(\mathbf{y}=\mathbf{Ax}\)我们可知

\[\begin{bmatrix} | \\ \mathbf{y} \\ | \end{bmatrix} = \begin{bmatrix} - & \mathbf{r}_1 & - \\ - & \mathbf{r}_2 & - \\ - & \mathbf{r}_3 & - \end{bmatrix} \begin{bmatrix} | \\ \mathbf{x} \\ | \end{bmatrix} \]

\[y_i = \mathbf{r}_i \cdot \mathbf{x} \]

\(\mathbf{y}\)的第\(i\)个分量实际上是矩阵的第\(i\)个行向量和\(\mathbf{x}\)点积的结果，这实际上就是把\(\mathbf{x}\)投影到了\(\{\mathbf{r}_1,\mathbf{r}_2,\mathbf{r}_3\}\)这个坐标系中，且投影的结果为\(\mathbf{y}\)。此外从另一个角度我们还可以知道

\[\begin{bmatrix} | \\ \mathbf{y} \\ | \end{bmatrix} = \begin{bmatrix} | & | & | \\ \mathbf{c}_1 & \mathbf{c}_2 & \mathbf{c}_3 \\ | & | & | \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} \]

\[\mathbf{y}=x_1\mathbf{c}_1+x_2\mathbf{c}_2+x_3\mathbf{c}_3 \]

这实际上就是以\(\mathbf{c}_1\)、\(\mathbf{c}_2\)、\(\mathbf{c}_3\)为基向量建立坐标系，并且以在这个坐标系中的坐标\((x_1,x_2,x_3)\)得到\(\mathbf{y}\)。上述的两个角度提供了独到的见解来了解\(\mathbf{y}=\mathbf{Ax}\)这一抽象操作中的几何含义。

矩阵的特殊类型（Special Types of Matrices）

  矩阵有些特殊的类型，比如单位矩阵就是对角矩阵（Diagonal Matrix），这种矩阵的非零元素只出现在对角线上。此外单位矩阵的转置等于它本身，这种有对称性的矩阵就叫做对称矩阵（Symmetric Matrix）。最后单位矩阵还是正交矩阵（Orthogonal Matrix），因为这种矩阵的每一列的向量与它当中的其它列向量都相互垂直。正交矩阵的行列式非\(+1\)即\(-1\)，而且有个非常好的性质

\[\mathbf{R}^\mathrm{T}\mathbf{R}=\mathbf{I}=\mathbf{R}\mathbf{R}^\mathrm{T} \]

利用之前提到过的对矩阵变换向量的理解可以很容易得到这个结论，下面有些矩阵的例子

\[\begin{bmatrix} 8 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 9 \end{bmatrix} \]

这个矩阵是对角矩阵也是对称矩阵，不是正交矩阵

\[\begin{bmatrix} 1 & 1 & 2 \\ 1 & 9 & 7 \\ 2 & 7 & 1 \end{bmatrix} \]

这个矩阵是对称矩阵，不是对角矩阵也不是正交矩阵

\[\begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{bmatrix} \]

这个矩阵是正交矩阵，不是对角矩阵也不是对称矩阵

使用矩阵和行列式计算（Computing with Matrices and Determinants）

  之前的部分提到，取n个n维向量的行列式，是由这n个n维向量定义的n维平行体的n维有符号容积决定的，对于二维来说就是由向量围成的平行四边形的面积。我们可以使用矩阵解决行列式计算的机制，假设有二维向量\(\mathbf{r}\)和\(\mathbf{s}\)，我们表示行列式为\(|\mathbf{r} \mathbf{s}|\)，它的值是由向量围成的平行四边形的有符号面积。假设有笛卡尔坐标的两个二维向量\((a,b)\)、\((A,B)\)，行列式可以这么写

\[\begin{vmatrix} \begin{bmatrix} a \\ b \end{bmatrix} \begin{bmatrix} A \\ B \end{bmatrix} \end{vmatrix} \equiv \begin{vmatrix} a & A \\ b & B \end{vmatrix} = aB-Ab \]

  最开始的部分提到用暴力展开计算行列式，不过使用那个方法计算会遇到许多\(0\)系数，而且还会遇到很多正负号，行列式计算的一个标准方法就是拉普拉斯展开（Laplace's Expansion），使用这个方法计算的关键就是找到余子式（Cofactor），方块矩阵的每个元素都有一个余子式，这个余子式是当前方块矩阵少一行少一列的行列式，而且每个余子式的符号由所属元素所在的行和列决定，如果行列相加为偶符号为正反之为负，因此可以得到符号矩阵

\[\begin{bmatrix} + & - & + & - & \cdots \\ - & + & - & + & \cdots \\ + & - & + & - & \cdots \\ - & + & - & + & \cdots \\ \vdots & \vdots & \vdots & \vdots & \ddots \end{bmatrix} \]

对于下面的\(4 \times 4\)矩阵来说

\[\mathbf{A}=\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix} \]

第一行的余子式是

\[a^{c}_{11} = \begin{vmatrix} a_{22} & a_{23} & a_{24} \\ a_{32} & a_{33} & a_{34} \\ a_{42} & a_{43} & a_{44} \end{vmatrix},a^{c}_{12} = - \begin{vmatrix} a_{21} & a_{23} & a_{24} \\ a_{31} & a_{33} & a_{34} \\ a_{41} & a_{43} & a_{44} \end{vmatrix} , a^{c}_{13} = \begin{vmatrix} a_{21} & a_{22} & a_{24} \\ a_{31} & a_{32} & a_{34} \\ a_{41} & a_{42} & a_{44} \end{vmatrix},a^{c}_{14} = - \begin{vmatrix} a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ a_{41} & a_{42} & a_{43} \end{vmatrix} \]

矩阵的行列式就是累加某列或某行的每个元素与它们的余子式的乘积，以第二列为例

\[|\mathbf{A}| = a_{12}a^{c}_{12} + a_{22}a^{c}_{22} + a_{32}a^{c}_{32} + a_{42}a^{c}_{42} \]

剩下要做的就是展开\(a^{c}_{12}\)、\(a^{c}_{22}\)、\(a^{c}_{32}\)、\(a^{c}_{42}\)以及后续的余子式。

计算逆（Computing Inverse）

  行列式的标准计算方法也给了我们一个工具来计算矩阵的逆，通过上个部分的拉普拉斯展开，我们可以知道一个\(4 \times 4\)的矩阵\(\mathbf{A}\)的逆\(\mathbf{A}^{-1}\)为

\[\mathbf{A}^{-1} = \frac{1}{|\mathbf{A}|} \begin{bmatrix} a^{c}_{11} & a^{c}_{21} & a^{c}_{31} & a^{c}_{41} \\ a^{c}_{12} & a^{c}_{22} & a^{c}_{32} & a^{c}_{42} \\ a^{c}_{13} & a^{c}_{23} & a^{c}_{33} & a^{c}_{43} \\ a^{c}_{14} & a^{c}_{24} & a^{c}_{34} & a^{c}_{44} \end{bmatrix} \]

等式右侧的矩阵实际上是把矩阵的每个元素替换成它的余子式所得到的矩阵的转置，把它与\(\mathbf{A}\)相乘可得到对角线上的元素为

\[\begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \end{bmatrix} \begin{bmatrix} a^{c}_{11} & \cdot & \cdot & \cdot \\ a^{c}_{12} & \cdot & \cdot & \cdot \\ a^{c}_{13} & \cdot & \cdot & \cdot \\ a^{c}_{14} & \cdot & \cdot & \cdot \\ \end{bmatrix} = \begin{bmatrix} |\mathbf{A}| & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \end{bmatrix} \]

非对角线上的元素为

\[\begin{bmatrix} \cdot & \cdot & \cdot & \cdot \\ a_{21} & a_{22} & a_{23} & a_{24} \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \end{bmatrix} \begin{bmatrix} a^{c}_{11} & \cdot & \cdot & \cdot \\ a^{c}_{12} & \cdot & \cdot & \cdot \\ a^{c}_{13} & \cdot & \cdot & \cdot \\ a^{c}_{14} & \cdot & \cdot & \cdot \\ \end{bmatrix} = \begin{bmatrix} \cdot & \cdot & \cdot & \cdot \\ 0 & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot \\ \end{bmatrix} \]

因为可以从\(a_{21}a^{c}_{11} + a_{22}a^{c}_{12} + a_{23}a^{c}_{13} + a_{24}a^{c}_{14}\)得到另外一个矩阵

\[\mathbf{B}=\begin{bmatrix} a_{21} & a_{22} & a_{23} & a_{24} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix} \]

这个矩阵是奇异的，因此它的行列式\(a_{21}a^{c}_{11} + a_{22}a^{c}_{12} + a_{23}a^{c}_{13} + a_{24}a^{c}_{14}\)求出来为\(0\)。

线性系统（Linear Systems）

有时我们可能会遇到由\(n\)个等式\(n\)个未知量组成的线性方程组，以\(n=3\)为例

\[\begin{align*} &3x+7y+2z=4 \\ &2x-4y-3z=-1 \\ &5x+2y+z=1 \end{align*} \]

我们可以写成如下形式

\[\begin{bmatrix} 3 & 7 & 2 \\ 2 & -4 & -3 \\ 5 & 2 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 4 \\ -1 \\ 1 \end{bmatrix} \]

使用克拉默法则（Cramer's rule）可以得到

\[x = \frac{\begin{vmatrix} 4 & 7 & 2 \\ -1 & -4 & -3 \\ 1 & 2 & 1 \end{vmatrix}}{\begin{vmatrix} 3 & 7 & 2 \\ 2 & -4 & -3 \\ 5 & 2 & 1 \end{vmatrix}},y = \frac{\begin{vmatrix} 3 & 4 & 2 \\ 2 & -1 & -3 \\ 5 & 1 & 1 \end{vmatrix}}{\begin{vmatrix} 3 & 7 & 2 \\ 2 & -4 & -3 \\ 5 & 2 & 1 \end{vmatrix}},z = \frac{\begin{vmatrix} 3 & 7 & 4 \\ 2 & -4 & -1 \\ 5 & 2 & 1 \end{vmatrix}}{\begin{vmatrix} 3 & 7 & 2 \\ 2 & -4 & -3 \\ 5 & 2 & 1 \end{vmatrix}} \]

这里要注意的是分母也就是矩阵的行列式\(|\mathbf{A}|\)不能为\(0\)，如果为\(0\)那么意味着方程没有唯一解。

特征值和矩阵对角化（Eigenvalues and Matrix Diagonalization）

  有些方块矩阵有特征值（Eigenvalues）和特征向量（Eigenvectors），特征向量是非零的且与矩阵相乘时方向不变，现有矩阵\(\mathbf{A}\)和向量\(\mathbf{a}\)，可以得到

\[\mathbf{Aa}=\lambda\mathbf{a} \]

公式中的\(\lambda\)就是和特征向量关联的特征值，矩阵的特征值和特征向量在很多应用中很有用。接下来先为矩阵求特征值和特征向量。我们有\(\mathbf{Aa}=\lambda\mathbf{a}\)，因此可以得到

\[\mathbf{Aa}=\lambda\mathbf{Ia} \]

这里的\(\mathbf{I}\)为单位矩阵，因此可以得到

\[\begin{align*} \mathbf{Aa}-\lambda\mathbf{Ia} &=0 \\ (\mathbf{A}-\lambda\mathbf{I})\mathbf{a} &=0 \end{align*} \]

因为\(\mathbf{a}\)不为\(0\)向量，所以\(\mathbf{A}-\lambda\mathbf{I}\)为奇异矩阵，这就使得它的行列式为\(0\)，因此我们可以计算出特征值\(\lambda\)，求出特征值\(\lambda\)后可以利用\((\mathbf{A}-\lambda\mathbf{I})\mathbf{a}=0\)为每个特征值\(\lambda\)求出关联的特征向量\(\mathbf{a}\)。
  有一个非常重要的特殊情况就是当矩阵为对称矩阵时，它的特征值和特征向量很简单，而且这种矩阵可以对角化变成如下形式

\[\mathbf{A}=\mathbf{QDQ}^\mathrm{T} \]

这里的\(\mathbf{Q}\)是正交矩阵，\(\mathbf{D}\)是对角矩阵。\(\mathbf{Q}\)的每一列是特征向量，\(\mathbf{D}\)的对角线上的元素是\(\mathbf{A}\)的特征值。把\(\mathbf{A}\)以这种形式分解就叫做特征值分解（Eigenvalue Decomposition），因为这样分解能揭示矩阵的特征向量和特征值。下面以一个\(2 \times 2\)的对称矩阵为例。

给定矩阵

\[\mathbf{A} = \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} \]

可以得到

\[\lambda^{2}-3\lambda+1=0 \]

可以解出\(\lambda\)为

\[\lambda = \frac{3 \pm \sqrt{5}}{2}, \approx \begin{bmatrix} 2.618 \\ 0.382 \end{bmatrix} \]

把\(\lambda=2.618\)带入\((\mathbf{A}-\lambda\mathbf{I})\mathbf{a} =0\)可得

\[\begin{bmatrix} 2-2.618 & 1 \\ 1 & 1-2.618 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} \]

特征向量约等于\((0.8507,0.5257)\)，对于另一个特征值\(\lambda = 0.382\)，与它关联的特征向量为\((-0.5257,0.8507)\)，因此可以把\(\mathbf{A}\)分解为

\[\begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} 0.8507 & -0.5257 \\ 0.5257 & 0.8507 \end{bmatrix} \begin{bmatrix} 2.618 & 0 \\ 0 & 0.382 \end{bmatrix} \begin{bmatrix} 0.8507 & 0.5257 \\ -0.5257 & 0.8507 \end{bmatrix} \]

奇异值分解（Singular Value Decomposition）

  通过上一个部分我们可以知道对称矩阵可以被对角化，然而我们遇到的大部分矩阵可能都不是对称的，因此有个更加通用的方法叫奇异值分解（Singular Value Decomposition，SVD），使用这个方法可以把矩阵分解为

\[\mathbf{A}=\mathbf{USV}^\mathrm{T} \]

其中\(\mathbf{U}\)和\(\mathbf{V}\)是可能不同的正交矩阵，前者的每列是\(\mathbf{A}\)的左奇异向量，后者的每列是\(\mathbf{A}\)的右奇异向量。\(\mathbf{S}\)是对角矩阵，对角线上面的每个元素是\(\mathbf{A}\)的奇异值。为了得到奇异值和奇异向量，我们可以在\(\mathbf{A}\)的基础上构造对称矩阵\(\mathbf{M}\)

\[\mathbf{M}=\mathbf{AA}^\mathrm{T}=(\mathbf{USV}^\mathrm{T})(\mathbf{USV}^\mathrm{T})^{\mathrm{T}}=\mathbf{US(V^{\mathrm{T}}V)SU^{\mathrm{T}}}=\mathbf{US}^{2}\mathbf{U}^\mathrm{T} \]

接下来可以通过\(\mathbf{M}\)求出\(\mathbf{U}\)和\(\mathbf{S}\)接着利用\(\mathbf{A}=\mathbf{USV}^\mathrm{T}\)求出\(\mathbf{V}\)，以下面的矩阵为例

\[\mathbf{A}=\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix},\mathbf{M}=\mathbf{AA}^\mathrm{T}=\begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} \]

由上个部分的计算可以得到

\[\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 0.8507 & -0.5257 \\ 0.5257 & 0.8507 \end{bmatrix} \begin{bmatrix} \sqrt{2.618} & 0 \\ 0 & \sqrt{0.382} \end{bmatrix} \mathbf{V}^\mathrm{T} \]

那么

\[\mathbf{V}=(\mathbf{S}^{-1}\mathbf{U}^\mathrm{T}\mathbf{A})^\mathrm{T} \]

因此

\[\begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} =\mathbf{U} \begin{bmatrix} \sigma_{1} & 0 \\ 0 & \sigma_{2} \end{bmatrix} \mathbf{V}^\mathrm{T} = \begin{bmatrix} 0.8507 & -0.5257 \\ 0.5257 & 0.8507 \end{bmatrix} \begin{bmatrix} 1.618 & 0 \\ 0 & 0.618 \end{bmatrix} \begin{bmatrix} 0.5257 & 0.8507 \\ -0.8507 & 0.5257 \end{bmatrix} \]

式中的\(\sigma_{i}\)是矩阵的第\(i\)个奇异值的标准符号。