《Fundamentals of Computer Graphics》第四章 光线追踪

开篇

  计算机图形学的基础任务之一是渲染（Rendering）三维物体，即利用在三维空间中排布的物体所构成的场景，计算出场景在某一视点（Viewpoint）观察得到的二维图像，这实际上和数世纪以来一些建筑师和工程师使用绘图与其他人交流他们的设计一样。
  从根本上来说，渲染是一个接受一系列物体的输入，然后产生像素数组输出的过程。不管怎么样，渲染涉及到考虑每个物体对每个像素的贡献，而且可以被分为两种一般方法。第一种是物体顺序渲染（Object-Order Rendering），这种渲染方法以每个物体为中心，为每个物体找到它能影响的像素并且更新像素值。第二种是图像顺序渲染（Image-Order Rendering），这种方式以每个像素为中心，为每个像素找到能影响到当前像素的物体并且计算像素值。你可以用嵌套循环来思考这两种方法的区别，在图像顺序渲染中，for each pixel在外面，然而在物体顺序渲染中，for each object在外面。
  使用这两种方法实际上能计算出完全一样的图像，但是因为它们的区别，导致了不同的计算效果，而且有截然不同的性能特性。在我们讨论完这两个方法后，我们将在第九章探索这两种方法的比较优势。但是广地来说，使用图像顺序渲染更容易得到能用的结果而且在能产生的效果上更加灵活，不过通常要花费更多的执行时间来得到相似的图像。
  光线追踪就是一个用于渲染三维场景的图像顺序算法，我们首先考虑这个，因为开发一个能用的光线追踪器相比于物体顺序渲染而言，不需要开发额外的数学工具。

基础的光线追踪算法（The Basic Ray-Tracing Algorithm）

  一个光线追踪器通过为每个像素计算而工作，对于每个像素来说，基础的任务就是找到在图像中当前像素位置能看到的物体。每个像素会往不同方向“看”，任何被像素看到物体必定会和视线（Viewing Ray）相交。而且看到的应该是与视线相交并且距离相机最近的物体，正是因为被看到的物体遮蔽了它后面的物体。一旦找到了目标物体，接着就要利用位置、表面法线等交汇点的信息进行着色（Shading），从而计算出像素的颜色。下图是个比较形象的交汇检测的例子

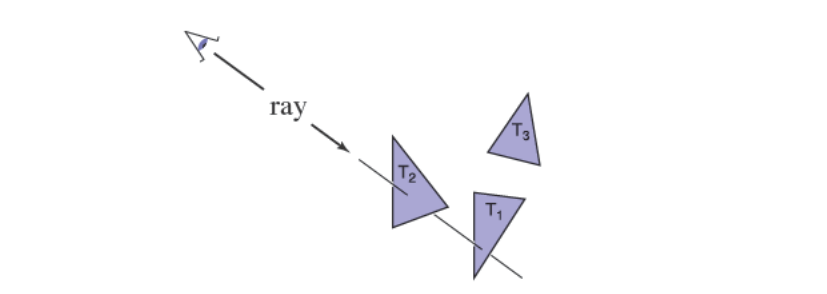
因此基础的光线追踪器应该包括三个部分：

1. 光线生成：它基于相机几何为每个像素计算视线的起点（Origin）和方向（Direction）。
2. 光线交汇：它为视线找到最近的物体。
3. 着色：它基于光线交汇的的结果为像素计算颜色。

基础的光线追踪程序对每个像素的计算流程应该如下：

1. 计算视线。
2. 找到视线击中的最近物体和表面法线。
3. 基于击中点、光源、法线计算并设置像素的颜色。

透视（Perspective）

  在计算机之前的数百年间，一些艺术家一直在研究使用二维绘画来表示三维物体或场景的问题，照片也通过二维图像表示三维场景。对于制造图像来说其实有许多不一般的方式，从立体派绘画到鱼眼镜头再到外围摄像机。对于艺术和摄影还有计算机图形学来说，一般途径就是线性透视（Linear Perspective），在这个途径中，三维物体通过在场景中的直线在图像中依旧是直线这种投影方式被投影到图像平面（Image Plane）上。
  最简单的一种投影类型就是平行投影（Planar Projection），如下图所示

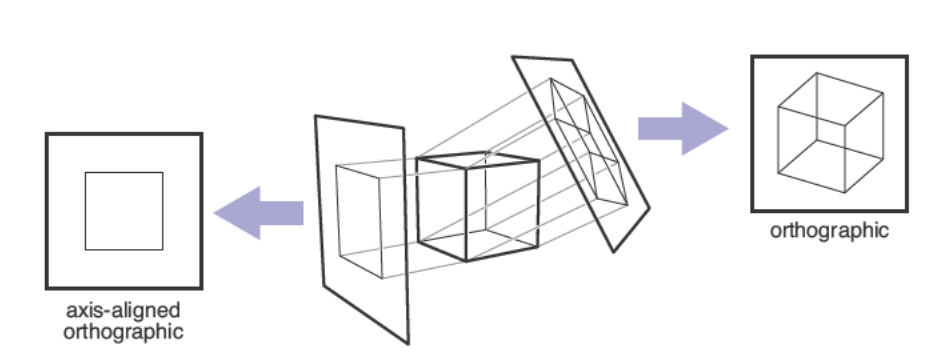
三维点通过跟随投影方向（Projection Direction）移动，从而被映射到图像平面上。视图是由投影方向和图像平面的选择决定的，如果图像平面和观察方向垂直，那么这种平行投影叫正投影（Orthographic），否则就是斜投影（Oblique）。
  平行投影通常用于机械以及建筑绘图，因为这个方法可以让相互平行的直线投影后依然平行，当平面物体平行于图像平面时，还能保留大小以及形状。但是它的优势同时也是它的劣势，在我们的日常生活体验中，远离我们的物体看起来会更小，因此在空间中平行的直线由我们观察可能不会平行。这是因为人眼和相机不会从一个方向收集光照信息，反而是通过从某个位置观察，收集四面八方来的光线。早在文艺复新时期，艺术家们已经认可使用透视投影（Perspective Projection）来生成看起来自然的视图，使用这种投影方法只需要让三维点跟随过视点的直线移动，如下图所示

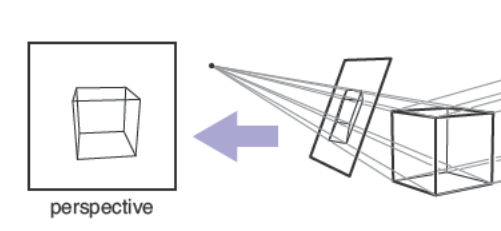
这样，离视点越远的物体在投影后会自然地变小。一个透视视图是是通过视点和图像平面的选择决定的，和平行视图一样有斜角透视视图和非斜角透视视图，它们之间的区别就在于图像中心处的投影方向。
  你可能已经了解了艺术中使用的三点透视（Three-point Perspective）规则，不过我们只需要遵循这之下的数学规则，就能实现透视投影效果。

计算观察光线（Computing Viewing Rays）

  在上个部分，生成光线基本的工具就是视点和图像平面，有许多方法能得到相机几何的细节，在这个部分我们介绍一个方法，基于单位正交基，支持正平行、斜平行、正交投影视图。
  为了生成光线，我们首先需要光线的数学表达。一条光线仅仅是由一个起始点和一个传播方向构成。我们可以使用三维参数直线描述光线，即

\[\mathbf{p}(t)=\mathbf{e}+t(\mathbf{s}-\mathbf{e}) \]

这个参数直线可以理解为从\(\mathbf{e}\)点出发，沿\(\mathbf{s}-\mathbf{e}\)方向传播，从而找到点\(\mathbf{p}\)。对于给定的\(t\)，我们就可以知道\(\mathbf{p}\)点在哪。在这个参数方程中点\(\mathbf{e}\)为光线起点，\(\mathbf{s}-\mathbf{e}\)为光线方向。下图是个形象的例子

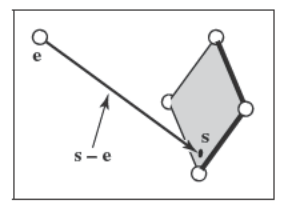
  这里要注意的是\(\mathbf{p}(0)=\mathbf{e}\)还有\(\mathbf{p}(1)=\mathbf{s}\)，如果计算出两个交汇参数\(t\)且满足\(0<t_1<t_2\)，那么可知\(\mathbf{p}(t_1)\)相比\(\mathbf{p}(t_2)\)距离眼睛更近。如果\(t<0\)，那么交点在眼睛后面。当要寻找离光线起始点最近的物体并且满足不在眼睛后方的条件时，这个事实会很有用。
  光线在一些结构或者对象中是不变的，一般都存储位置和方向。以面向对象的程序为例，我们可能这么写代码：

class Ray
    Vec3 o | 光线起点
    Vec3 d | 光线方向
    Vec3 evaluate(real t)
        return o+td

上述代码假设有个Vec3类代表着三维向量并且支持基本的算术操作。
  为了计算一条观察光线，我们需要知道\(\mathbf{e}\)点和\(\mathbf{s}\)点，找到\(\mathbf{s}\)点可能有点困难，但是当我们在右手坐标系中看待这一问题时，答案还是挺直接的。
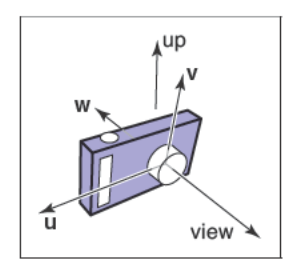
  我们所有的光线生成方法都是从一个叫相机帧（Camera Frame）的单位正交基开始的，通过\(\mathbf{e}\)作为视点还有\(\mathbf{u}\)、\(\mathbf{v}\)、\(\mathbf{w}\)作为三个基向量确定。其中\(\mathbf{u}\)指向右方，\(\mathbf{v}\)指向上方，\(\mathbf{w}\)指向后方，因此\(\{\mathbf{u},\mathbf{v},\mathbf{w}\}\)构成了一个右手坐标系。使用最通常的方法来构造相机帧得首先确定视点也就是\(\mathbf{e}\)，接着确定观察方向也就是-\(\mathbf{w}\)，然后确定上向量（Up Vector）\(\mathbf{v}\)，最后通过第二章中的方法确定右向量\(\mathbf{u}\)。

正交视图（Orthographic Views）

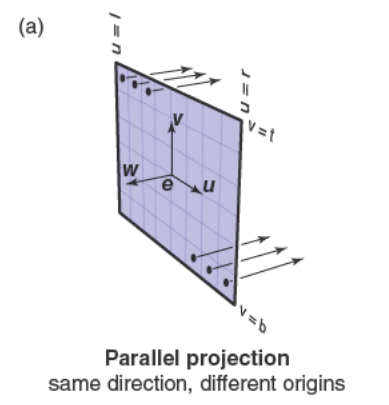
  对于一个正交视图，所有的光线都有方向\(-\mathbf{w}\)，尽管平行视图没有视点，但是我们可以使用相机帧的原点来定义光线出发的平面。
  观察光线应该从以点\(\mathbf{e}\)、向量\(\mathbf{u}\)和向量\(\mathbf{v}\)确定的平面出发，最后一个要确定的信息就是图像平面应该在哪。我们直接使用四个数来定义图像维度也就是图像的四边，其中\(l\)和\(r\)分别为图像的左边和右边位置，长度通过从\(\mathbf{e}\)点出发沿着\(\mathbf{u}\)方向测量。\(b\)和\(t\)分别为图像的底边和顶边位置，长度通过从\(\mathbf{e}\)点出发沿着\(\mathbf{v}\)方向测量。通常来说这四个量满足\(l<0<r\)且\(b<0<t\)。
  假设图像维度为\(n_x \times n_y\)，为了把这个图像填充到\((r-l)\times(t-b)\)的矩形空间中，像素中心处之间的水平间距和竖直间距分别为\((r-l)/n_x\)和\((t-b)/n_y\)。像素位置\((i,j)\)可以用如下公式把它映射到图像平面的位置\((u,v)\)

\[u=l+(r-l)(i+0.5)/n_x \]

\[v=b+(t-b)(j+0.5)/n_y \]

有了\((u,v)\)后接下来我们可以为正交视图计算观察光线

\[\mathrm{ray.o} \leftarrow \mathbf{e}+u\cdot\mathbf{u}+v\cdot\mathbf{v} \]

\[\mathrm{ray.d} \leftarrow -\mathbf{w} \]

创建斜平行视图很简单，直接改变ray.d即可，下图是一个比较形象的正交视图演示

透视视图（Perspective Views）

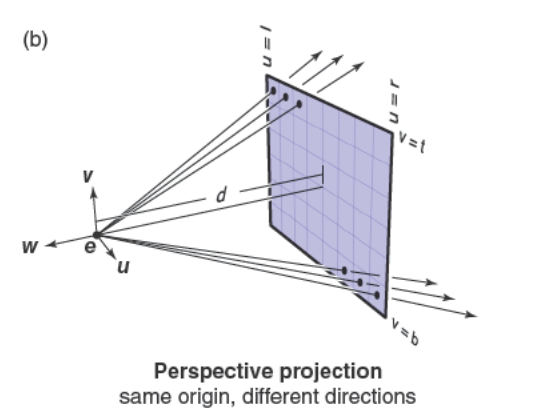
  对于透视视图来说，所有的光线都有相同的起点也就是视点，但是方向是不同的。图像平面也不在\(\mathbf{e}\)处，距离\(\mathbf{e}\)的距离为\(d\)，这段距离是图像平面距离也被称为焦距（Focal Length），因为\(d\)在真实的摄像机中是焦距。光线方向是通过视点以及像素在图像平面的位置定义的，为透视视图计算光线的流程如下

1. 利用之前提到的方法计算\((u,v)\)
2. \(\mathrm{ray.o} \leftarrow \mathbf{e}\)
3. \(\mathrm{ray.d} \leftarrow -d\cdot\mathbf{w} + u\cdot\mathbf{u} + v\cdot\mathbf{v}\)

斜角透视视图可以通过分别声明图像平面的法线和投影方向来得到。下图是一个比较形象的透视视图演示

光线物体交汇（Ray-Object Intersection）

  一旦我们生成了光线\(\mathbf{e}+t\mathbf{d}\)，接下来要做的事就是找到第一个交点且\(t>0\)。在实践中变成了找到光线在区间\([t_0,t_1]\)与表面的交点。基础的光线交汇情况是当\(t_0=0\)且\(t_1=+\infty\)的时候。接下来的部分将为球面和三角形解决这个问题。

光线球面交汇（Ray-Sphere Intersection）

现在已知光线\(\mathbf{p}(t)=\mathbf{e}+t\mathbf{d}\)以及球面的隐式函数

\[(x-x_c)^2+(y-y_c)^2+(z-z_c)^2-R^2=0 \]

把\(\mathbf{p}\)带入隐式函数可得

\[(\mathbf{p}-\mathbf{c})\cdot(\mathbf{p}-\mathbf{c})-R^2=0 \]

因此可得

\[(\mathbf{d}\cdot\mathbf{d})t^2+2\mathbf{d}\cdot(\mathbf{e}-\mathbf{c})t+(\mathbf{e}-\mathbf{c})\cdot(\mathbf{e}-\mathbf{c})-R^2=0 \]

这个等式实际上是一个一元二次方程\(At^2+Bt+C=0\)，不过首先得通过判别式（Discriminant）也就是\(B^2-4AC\)来获得根的情况，如果是负数那么没有根也就是没有交点，相反如果是正的那么有两个根也就是两个交点，如果等于\(0\)那么只有一个根也就是一个交点。接着使用求根公式可以得到

\[t=\frac{-\mathbf{d}\cdot(\mathbf{e}-\mathbf{c})\pm \sqrt{(\mathbf{d}\cdot(\mathbf{e}-\mathbf{c}))^2-(\mathbf{d}\cdot\mathbf{d})((\mathbf{e}-\mathbf{c})\cdot(\mathbf{e}-\mathbf{c})-R^2)}}{(\mathbf{d}\cdot\mathbf{d})} \]

在实践中应该先检测判别式，在区间\([t_0,t_1]\)中找到的交点中，如果更小的根在这个区间中那么取更小的根，相反取更大的根，以上两种情况都不符合就认为光线没有击中表面。求得交点后下一步就是求法线\(\mathbf{n}\)，对于球面来说其实很简单，\(\mathbf{n}=(\mathbf{p}-\mathbf{c})/R\)。

光线三角形交汇（Ray-Triangle Intersection）

  有许多算法可以计算光线和三角形的交点，这里介绍一种求重心坐标的方法。

现在已知光线\(\mathbf{p}(t)=\mathbf{e}+t\mathbf{d}\)以及三角形三点\(\mathbf{a}\)、\(\mathbf{b}\)、\(\mathbf{c}\)，可知

\[\mathbf{e}+t\mathbf{d}=\mathbf{a}+\beta(\mathbf{b}-\mathbf{a})+\gamma(\mathbf{c}-\mathbf{a}) \]

其中\(\beta>0\)、\(\gamma>0\)、\(\beta+\gamma<1\)，为了求解\(t\)、\(\beta\)、\(\gamma\)我们展开上方的等式为

\[x_e+tx_d=x_a+\beta(x_b-x_a)+\gamma(x_c-x_a) \]

\[y_e+ty_d=y_a+\beta(y_b-y_a)+\gamma(y_c-y_a) \]

\[z_e+tz_d=z_a+\beta(z_b-z_a)+\gamma(z_c-z_a) \]

可以重写为向量矩阵相乘形式

\[\begin{bmatrix} x_a-x_b & x_a-x_c & x_d \\ y_a-y_b & y_a-y_c & y_d \\ z_a-z_b & z_a-z_c & z_d \end{bmatrix} \begin{bmatrix} \beta \\ \gamma \\ t \end{bmatrix} = \begin{bmatrix} x_a-x_e \\ y_a-y_e \\ z_a-z_e \end{bmatrix} \]

因此可以使用克拉默法则求解

\[\beta = \frac{\begin{vmatrix} x_a-x_e & x_a-x_c & x_d \\ y_a-y_e & y_a-y_c & y_d \\ z_a-z_e & z_a-z_c & z_d \end{vmatrix} }{|\mathbf{A}|} \]

\[\gamma = \frac{\begin{vmatrix} x_a-x_b & x_a-x_e & x_d \\ y_a-y_b & y_a-y_e & y_d \\ z_a-z_b & z_a-z_e & z_d\end{vmatrix}}{|\mathbf{A}|} \]

\[t = \frac{\begin{vmatrix} x_a-x_b & x_a-x_c & x_a-x_e \\ y_a-y_b & y_a-y_c & y_a-y_e \\ z_a-z_b & z_a-z_c & z_a-z_e \end{vmatrix}}{|\mathbf{A}|} \]

\[\mathbf{A} = \begin{bmatrix} x_a-x_b & x_a-x_c & x_d \\ y_a-y_b & y_a-y_c & y_d \\ z_a-z_b & z_a-z_c & z_d \end{bmatrix} \]

  对于光线三角形的交汇算法来说，可以使用一些条件来更早地结束检测，因此函数应该像下面这样。

在软件中的光线交汇（Ray intersection in software）

  在光线追踪程序中，一个好的想法是使用面向对象的设计，例如有表面（Surface）类以及它的派生类三角形（Triangle）、球（Sphere）等等，任何能与光线交汇的都应该是表面的子类。表面类应该有的关键接口就是和光线交汇的方法。

class Surface
    HitRecord hit(Ray r,real t0,real t1)

这里的\(t_0\)和\(t_1\)用来指定方法返回区间\([t_0,t_1]\)内的击中情况，而返回的HitRecord包含了表面交汇点的数据

class HitRecord
    Surface s | 被击中的表面
    real t | 击中点的参数值
    Vec3 n | 击中点的表面法线
    .
    .
    .

被击中的表面、\(t\)值还有表面法线是HitRecord的最小需求，其它的数据例如纹理坐标或者切向向量可能也会被存储。根据语言或者实际写的代码，HitRecord可能不会直接被返回，而是使用引用传参HitRecord，接着让hit方法写入成员。未击中可以通过\(t=\infty\)来指定。

与一组物体交汇（Intersecting a Group of Objects）

  一个有趣的场景应该是由多个物体构成的，通常我们会检测光线与场景的交汇，我们必须找到在光线上且离相机最近的交点。最简单的方法就是与所有物体检测交汇，挑选出最小的参数\(t\)。

class Group,subclass of Surface
    list-of-Surface surfaces | 组中的所有表面
    HitRecord hit(Ray ray,real t0,real t1)
        HitRecord closest-hit(inf) | 使用未命中情况初始化最近的交点
        for surf in surfaces do
            rec = surf.hit(ray,t0,t1)
            if rec.t < inf then
                closest-hit = rec
                t1 = t
        return closest-hit

着色（Shading）

  一旦找到像素能看到的表面，接着就能通过着色模型（Shading Model）来计算像素值。着色模型有简单的启发式的还有基于物理的，要怎么做完全取决于你。下面的部分介绍如何利用基础的信息来进行着色。

光源（Light Sources）

  为了支持着色，一个光线追踪程序通常有一系列的光源。我们需要三种基础光源分别为点光源、定向光、环境光。其中点光源向四周均匀辐射能量，定向光从某个固定的方向点亮场景，环境光提供固定的光照。在更加绚丽的系统中通常有其它类型的光源，例如局部光源。
  利用点光源或者定向光计算着色需要某些几何信息，在光线追踪器中，当光线击中表面时我们就能得到以下必要的信息

• 着色点\(\mathbf{x}\)：通过参数值\(t\)计算。
• 表面法线\(\mathbf{n}\)：取决于表面的类型，每个表面都要能计算击中点的法线。
• 光照方向\(\mathbf{l}\)：通过光源的信息得到，如位置或方向。
• 观察方向\(\mathbf{v}\)：仅仅是归一化的光线反向向量 \((\mathbf{v} = -\mathbf{d}/||\mathbf{d}||)\)。

对于环境光来说就更简单，没有光照方向这种概念，因为在这种情况下光来自四面八方，而且光照着色也不依赖于\(\mathbf{v}\)，对于更加简单的环境光来说，甚至不会依赖于\(\mathbf{x}\)或\(\mathbf{n}\)。
  计算一个包含多个光源的场景的光照其实很简单，只需要把各个光源的着色结果累加起来。在基础的光线追踪器中，可以直接遍历所有光源积累光照结果。

在软件中的着色（Shading in software）

  一个光线追踪程序通常包含代表着光源和材质的类，光源可以是光源类的子类实例，它们必须包含足够的信息来描述光源。着色通常也需要参数来描述表面的材质，因此另一个有用的类就是材质（Material），它囊括了着色模型进行计算所需要的一切。
  不同的系统采取不同的措施来分开光源和材质之间的着色计算，一种和上述目标一致的方法是让光源负责总的光照计算，让材质负责双向反射分布函数（BRDF）值。有了以上这些，一些类以及所属的接口应该长这样

class Light
    Color illuminate(Ray ray,HitRecord hrec)

class Material
    Color evaluate(Vec3 l,Vec3 v,Vec3 n)

每个表面都会存储一份对它的材质的引用。点光源光照可能会以如下方式实现

class PointLight, subclass of Light
    Color I
    Vec3 p
    Color illuminate(Ray ray,HitRecord hrec)
        Vec3 x = ray.evaluate(hrec.t)
        real r = distance(p,x)
        Vec3 l = (p-x)/r
        Vec3 n = hrec.normal
        Color E = max(0,dot(n,l))*I/pow(r,2)
        Color k = hrec.surface.material.evaluate(l,v,n)
        return kE

常强度的环境光源可能会以如下方式实现

class AmbientLight, subclass of Light
    Color Ia
    Color illuminate(Ray ray,HitRecord hrec)
        Color ka=hrec.surface.material.ka
        return ka*Ia;

光线击中并且进行着色的代码可能像下面这样

function shade-ray(Ray ray,real t0,real t1)
HitRecord rec = scene.hit(ray,t0,t1)
if rec.t < inf then
    Color c = 0
    for light in scene.lights do
        c += light.illuminate(ray,rec)
    return c
else
    return background-color

下方为着色结果的一张示例图

阴影（Shadows）

  一旦光线追踪器中有了基础的着色，对于点光源以及定向光的阴影可以被简单地添加。我们只需发出阴影光线（Shadow Ray）来检测击中点是否能被光源“看到”。如果能被“看到”，那么就得计算着色结果，否则跳过这个光源的着色计算。阴影光线的例子如下图所示。

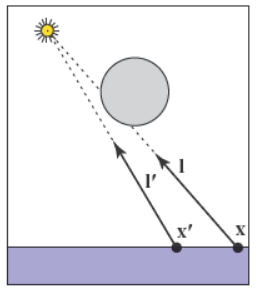
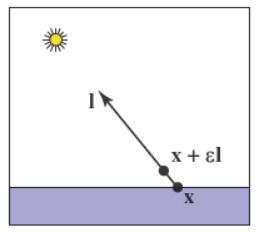
  理想点光源的阴影光线如左图所示，是以击中点为起点到点光源处为方向的光线，从\(\mathbf{x}\)位置发出的阴影光线击中了其它物体因此无法被点光源“看到”，所以无法被点光源影响。相反\(\mathbf{x}^\prime\)可以被点光源“看到”，从而能被点光源影响。理想定向光的阴影光线如右图所示，是以击中点为起点且方向固定的光线，检测逻辑与点光源一样。
  不过在实际情况下，由于数值精度的问题，一般会检测阴影光线在区间\([\epsilon,a]\)之内是否有交点，其中\(\epsilon\)是小的正常量来用来避免自遮蔽的情况，如右图所示。加入阴影后的着色结果如下图所示。

镜像反射（Mirror Reflection）

  加入理想情况下的镜面（Specular）反射也很直接，我们直接使用公式\(\mathbf{r}=\mathbf{d}-2(\mathbf{d}\cdot\mathbf{n})\mathbf{n}\)计算击中点处的反射光线即可。不过在现实世界中有些能量会随着在表面上的反射而损失，例如相对于蓝色来说，黄金反射黄色更多，我们可以使用\(k_m\)镜面反射颜色来描述这一现象。在进行实践时要注意反射光线应该同样使用\(\epsilon\)检测区间\([\epsilon,a]\)内的交点，就像阴影检测那样，因此着色代码变成了

color c = c + k_m*shade-ray(Ray(p,r),epsilon,inf)

加入镜面反射的着色结果如下图所示