《Fundamentals of Computer Graphics》第二章 杂项数学

开篇

  第二章“Miscellaneous Math”讲了许多高中、大学所学的一些基础数学知识：集合、映射、区间、三角函数、积分、密度函数等等。这里有一些要注意的地方。

立体角与球面三角学（Solid Angles and Spherical Trigonometry）

  传统的三角学涉及平面上的三角形，三角形也能定义在非平面表面。这种三角学在许多领域例如天文学出现，研究这些三角形的领域叫球面三角学。它虽然不会经常在图形学中被使用，但是出现的时候一般都非常重要。
  在球面三角学中对计算机图形学非常重要的一个概念叫立体角（Solid Angle），立体角让我们可以量化例如在天上的飞机占据视野的多少。整个测量过程其实很简单，把能“看到”飞机的所有方向投影到单位球，接着测量面积。测量出的面积大小就是立体角的大小，不过立体角的单位是Sr（Steradian），在单位球上的总立体角就是\(4\pi\,\mathrm{sr}\)。
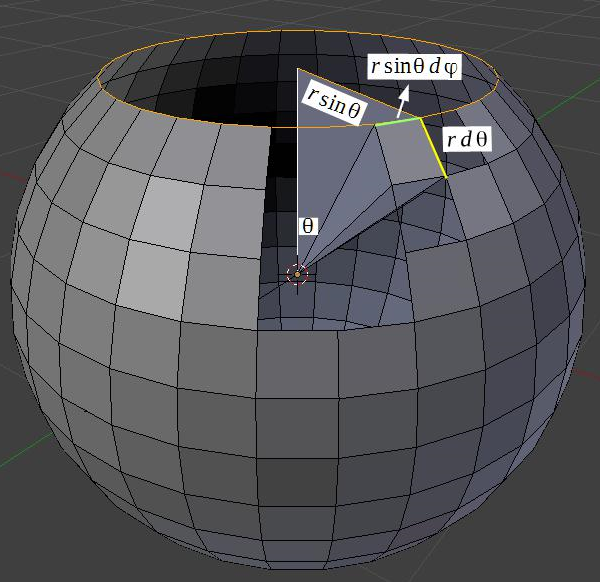
  此外，我还稍微查了下资料。wiki百科给出了立体角积分公式，这里可以稍微了解一下，能让你对立体角有更好的理解。首先通过\(\Delta \theta\)和\(\Delta \varphi\)分割半径为\(r\)的球面，如图所示。

作者：Travailen

当\(\Delta \theta\)和\(\Delta \varphi\)在极小情况下，分割出来的每一极小份的曲面可以被当作一个矩形。因此极小份的面积为

\[dA = (r\,\sin\theta\,d\varphi)(rd\theta) = r^2(\sin\theta\,d\theta\,d\varphi) \]

当\(r=1\)时，极小立体角的大小就是极小面积的大小

\[d\Omega = \sin\theta\,d\theta\,d\varphi \]

所以立体角的积分公式为

\[\Omega = \int \int_{S} \sin\theta\,d\theta\,d\varphi \]

单位正交基的确定

  有时候需要为给定的向量求一个标准正交基，比如在写全屏光线追踪着色器时，要为每个像素发出光线，这个时就需要一个标准正交基。对于给定的向量\(\mathbf{a}\)，我们需要标准正交基\(\mathbf{u}\)、\(\mathbf{v}\)、\(\mathbf{w}\)。其中\(\mathbf{w}\)与\(\mathbf{a}\)方向一致，\(\mathbf{u}\)、\(\mathbf{v}\)一般不关心是什么，书中给了以下两种方法。

从一个辅助向量构造（Constructing a Basis from a Single Vector）

  首先挑选一个不与\(\mathbf{w}\)共线的一个辅助向量\(\mathbf{t}\)，值得注意的是，辅助向量\(\mathbf{t}\)不可与\(\mathbf{w}\)过于接近，\(\mathbf{u}\)、\(\mathbf{v}\)、\(\mathbf{w}\)可以按如下公式进行计算。

\[\mathbf{w}=\frac{\mathbf{a}}{||\mathbf{a}||} \]

\[\mathbf{u}=\frac{\mathbf{t} \times \mathbf{w}}{||\mathbf{t} \times \mathbf{w}||} \]

\[\mathbf{v}=\mathbf{w} \times \mathbf{u} \]

从两个辅助向量构造（Constructing a Basis from Two Vectors）

  使用这个方法需要最好挑选两个垂直的向量\(\mathbf{a}\)、\(\mathbf{b}\)，要注意的是向量\(\mathbf{a}\)、\(\mathbf{b}\)不可过于接近，\(\mathbf{u}\)、\(\mathbf{v}\)、\(\mathbf{w}\)可以按如下公式进行计算。

\[\mathbf{w}=\frac{\mathbf{a}}{||\mathbf{a}||} \]

\[\mathbf{u}=\frac{\mathbf{b} \times \mathbf{w}}{||\mathbf{b} \times \mathbf{w}||} \]

\[\mathbf{v}=\mathbf{w} \times \mathbf{u} \]

重心坐标

 对于三角形\(ABC\)上的一点\(\mathrm{P}\)，它的重心坐标\((\alpha,\beta,\gamma)\)指代的是，三角形\(ABC\)每个顶点的位置占点\(\mathrm{P}\)位置的比重，即\(\vec{P} = \alpha \vec{A}+\beta\vec{B}+\gamma\vec{C}\)，而且有如下关系\(\alpha+\beta+\gamma=1\)。重心坐标对于属性的插值来说非常重要，而且在后面的代码实现中需要计算它。书中为了证明恒等于\(1\)这个关系，于是先引出了重心坐标的计算，反而导致证明过程非常复杂。我想了想有更简单的几何证明，方法如下。
  在三角形\(\mathrm{ABC}\)上做\(\mathrm{DE}\)平行于\(\mathrm{AC}\)，接着在线段\(\mathrm{DE}\)上取一点\(\mathrm{P}\)，如下图所示。

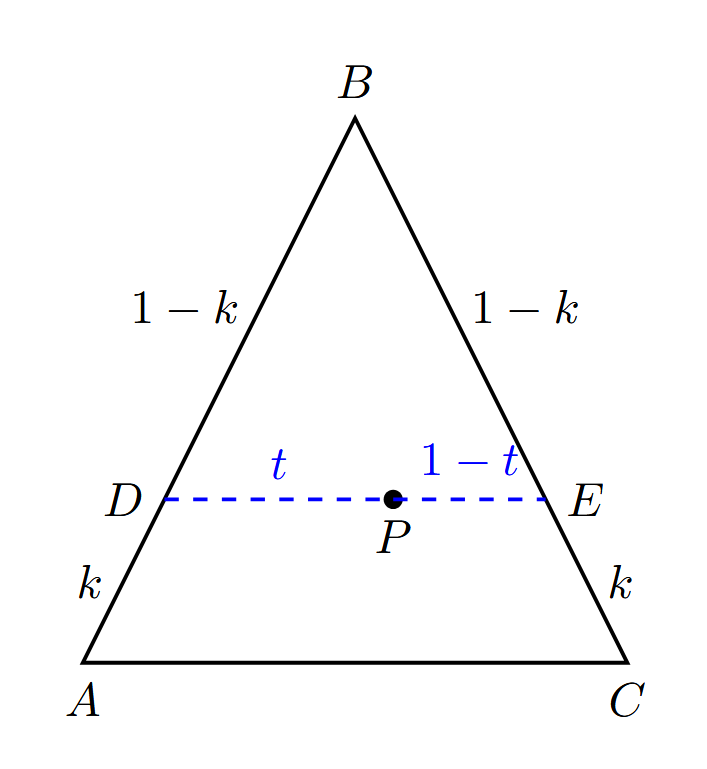
如图所示，现在可由两个系数\(k\)与\(t\)确定三角形\(\mathrm{ABC}\)上一点

\[\vec{P} = \vec{B}+(1-t)(1-k)(\vec{A}-\vec{B})+t(1-k)(\vec{C}-\vec{B}) \]

化简可得

\[\vec{P}=(1-t-k+tk)\vec{A}+k\vec{B}+(t-tk)\vec{C}=\alpha\vec{A}+\beta\vec{B}+\gamma\vec{C} \]

易得

\[\alpha=1-t-k+tk \]

\[\beta=k \]

\[\gamma=t-tk \]

因此可证得\(\alpha+\beta+\gamma=1\)。此外，由几何证明我们能得到显而易见的一点，当\(k\)线性变化时，点\(\mathrm{P}\)离线段\(\mathrm{AC}\)的距离也会线性变化，令点\(\mathrm{B}\)和点\(\mathrm{P}\)离线段\(\mathrm{AC}\)的距离分别为\(D_\mathrm{B}\)和\(D_\mathrm{P}\)，再次利用相似关系，于是有

\[\frac{D_\mathrm{P}}{D_\mathrm{B}-D_\mathrm{P}} = \frac{k}{1-k} \]

整理可得

\[k = \frac{D_\mathrm{P}}{D_\mathrm{B}} \]

某点\((x,y)\)距离直线\(f(x,y)=Ax+By+C=0\)的距离公式为

\[D = \frac{|Ax+By+C|}{\sqrt{A^2+B^2}} = \frac{|f(x,y)|}{\sqrt{A^2+B^2}} \]

令直线\(\mathrm{AC}\)的函数为\(f_\mathrm{AC}\)，那么有

\[\beta = k = \frac{|f_\mathrm{AC}(\mathrm{P})|}{|f_\mathrm{AC}(\mathrm{B})|} \]

又因为点\(\mathrm{B}\)和点\(\mathrm{P}\)在直线\(\mathrm{AC}\)同侧，所以可以去掉取绝对值操作，因此最终的求解公式为

\[\beta = \frac{f_\mathrm{AC}(\mathrm{P})}{f_\mathrm{AC}(\mathrm{B})} \]

对于其它两个重心坐标来说，我们只需要取其它两个直线函数以及与其它两个边对应的顶点计算即可。

蒙特卡洛积分（Monte Carlo Integration）

  蒙特卡洛积分就是通过随机样本来对函数的某区域进行积分。现要求沿表面法线方向的半球内入射光线所贡献的辐照度

\[H(\mathbf{n})=\int_{\Omega} L_f(\omega_i) \, (\mathbf{n} \cdot \omega_i) \, d\omega_i \]

可以通过数量为\(\mathrm{N}\)的随机采样点来获得辐亮度的积分值，每个采样点的权重是\(\frac{2\pi}{\mathrm{N}}\)，由此可写如下代码

const float3 dir = octDecode(coor.x, coor.y);

float3 result = float3(0.0, 0.0, 0.0);

[unroll]
for (uint i = 0; i < SAMPLECOUNT; i++)
{
    const float3 randDir = randomDirection[i] * sign(dot(dir, randomDirection[i]));

    const float3 radiance = envCube.SampleLevel(linearClampSampler, randDir, 0.0).rgb;

    result += radiance * saturate(dot(dir, randDir));
}
        
result = 2.0 * PI / float(SAMPLECOUNT) * result;

重要性采样（Importance Sampling）

  当被积函数在积分区域内的值有很大的变化时，我们可以把采样点集中分布在一些区域，不过这个时候每个采样点都有特定的非均匀权重。如果我们知道概率密度函数\(\mathrm{PDF}\)就能求出积分值，代码如下

const float3 dir = float3(0.0, 0.0, 1.0);

float3 result = float3(0.0, 0.0, 0.0);

[unroll]
for (uint i = 0; i < SAMPLECOUNT; i++)
{
    const float3 randDir = randomDirection[i];

    const float3 radiance = envCube.SampleLevel(linearClampSampler, randDir, 0.0).rgb;

    result += radiance * saturate(dot(dir, randDir)) / directionImportance[i];
}
        
result = 1.0 / float(SAMPLECOUNT) * result;