《Fundamentals of Computer Graphics》第一章 介绍

  在开头我要说几件重要的事。读完这本书后，主要想翻译一些重要章节的内容，而且会在某些地方加上自己的理解。英文原文差不多是看懂了的，就是有时候不知道该怎么恰当地翻译成中文，所以有时候会借助现有的翻译工具。再一个就是我的表达能力有点差（语文没学好），有些翻译错了或者感觉味道不对的地方，会加以改正的！

开篇

  计算机图形学这个术语描述的是使用计算机生成和处理图像的任何应用。这本书是关于基础算法和数学，特别是那些利用三维物体和场景生成合成图像的基础算法和数学。

主要领域（Graphics Areas）

  图形学涉及的主要领域有建模（Modeling）、渲染（Rendering）、动画（Animation）。

• 建模：它涉及到把形状和外观属性存储到计算机中的方法的数学规范。

• 渲染：这个术语来自艺术领域，它涉及到来自三维计算机模型的着色图像的生成。

• 动画：它是通过图像序列制造运动错觉的技术，虽然使用了建模和渲染，但是涉及到了随时间运动这一关键问题，这通常不会在基础的建模和渲染中涉及。

主要应用（Major Applications）

  它的主要应用有：视频游戏、卡通、视觉特效、动画电影、计算机辅助设计、计算机辅助制造、模拟、医学成像、信息可视化

图形API（Graphics APIs）

  使用图形库的一个关键的部分就是与图形API打交道。API（Application Program Interface）是进行一系列相关操作的标准函数集，那么图形API就是例如能把图像和三维表面绘制到屏幕上的窗口的图形函数集。
  每个图形程序都要能使用两种API，一种是用于视觉输出的图形API，另一种是获得用户的输入的用户界面API。关于图形和用户界面API，目前有两种主要的范例。第一种是集成方式，Java就是一个例子，在这之中，图形和用户界面是集成的而且是可移植的包，作为语言的一部分被完全地标准化和支持。第二种的例子有Direct3D和OpenGL，在这之中，绘制指令是软件库的一部分，这些软件库会和一个语言绑定，例如C++。此外，用户界面软件是一个独立的实体，在系统之间可能有不同。在第二种范例中，很难编写可移植的代码，尽管对于简单的程序来说，也许可以使用一个可移植的库封装层来封装系统特定的用户界面代码。

图形管线（Graphics Pipeline）

  现代的每台桌面计算机通常都有一个强大的三维图形管线（Graphics Pipeline），它是能高效地绘制三维图元的特殊软硬件子系统。通常，这些系统都被优化来处理有着共享顶点的三维三角形。在管线中的基础的操作就是把三维顶点位置映射到二维屏幕位置然后着色三角形，来让这些三角形看着很真实的同时又以正确的前后顺序展现到观察者眼前。
  尽管以从后往前的顺序绘制三角形在曾今是一个最重要的被研究的问题，现在通常都通过z缓冲（z-buffer）来解决，它通过使用一个特殊的内存缓冲以一种蛮力的方式解决了绘制顺序的问题。
  事实证明，在图形管线中使用的几何操作几乎都能在由三维传统坐标和齐次坐标（Homogeneous Coordinate）组成的四维坐标空间中所解决，第四个齐次坐标解决的是透视视图这一问题。四维坐标是通过\(4 \times 4\)的矩阵和四维向量操作的，图形管线因此有许多机制，用于高效地处理和组合这些矩阵和向量。四维坐标系统是用于计算机科学的最微妙且优美的构造之一，它也是学习计算机图形学要跨过的最大的一个障碍。
  图像生成速度很大程度上取决于要被绘制的三角形数量，在很多应用中交互性比视觉质量更加重要，减少用于表达模型的三角形的数量是很值得的。此外，模型会在不同的距离被观察，相比于近距离观察模型，在远距离观察时其实只需要绘制更少的三角形，因此采用细节等级（Level Of Detial，LOD）方案来表示模型是非常有用的。

数值问题（Numerical Issues）

  在进行实践的时候，有些时候会遇到一些很难处理的数值问题。幸运的是，当代的大多数计算机都遵循IEEE浮点数标准，它可以让程序员对某些数值情况的处理做出便捷的假设。对于图形学来，第一也是最重要的是理解下面的三种“特殊”值：

• 正无穷（\(+\infty\)）：它是一个比其它有效数字都大的一个有效数字。

• 负无穷（\(-\infty\)）：它是一个比其它有效数字都小的一个有效数字。

• 非数字（\(\mathrm{NaN}\)）：它会在进行未定义的操作后出现，例如除以\(0\)。

IEEE浮点数的设计者做了对编程者非常有利的一些决定，对于正实数\(a\)来说有

\[+a/(+\infty)=+0 \]

\[-a/(+\infty)=-0 \]

\[+a/(-\infty)=-0 \]

\[-a/(-\infty)=+0 \]

对于\(\infty\)和正实数\(a\)，相关的操作有

\[\begin{align*} \infty+\infty&=+\infty \\ \infty-\infty&=\mathrm{NaN} \\ \infty \times \infty&=\infty \\ \infty / \infty&=\mathrm{NaN} \\ \infty / a&=\infty \\ \infty / 0&=\infty \\ 0/0&=\mathrm{NaN} \end{align*} \]

此外涉及无穷值的布尔表达式有如下要注意的几点

1. 所有有限的有效数字都小于正无穷。

2. 所有有限的有效数字都大于负无穷。

3. 负无穷比正无穷小。

涉及非数字的表达式的处理规则有如下几点要注意

1. 任何包括非数字的算术表达式的结果都是非数字。

2. 任何包括非数字的布尔表达式的结果都为假。

对于正实数\(a\)除以0的操作有

\[+a/+0=+\infty \]

\[-a/+0=-\infty \]

  通过利用IEEE规则，许多数值计算可以变简单。例如，考虑如下表达式

\[a = \frac{1}{\frac{1}{b}+\frac{1}{c}} \]

在没有IEEE规则的情况下，除以零会导致程序崩溃，因此需要两个\(if\)语句来检查\(b\)或\(c\)是否非常小或为\(0\)。当使用IEEE规则时，如果\(b\)或\(c\)为\(0\)，那么\(a\)会为\(0\)。另一个常用的技巧是利用非数字的布尔属性来避免特殊情况的检查，考虑以下的代码片段

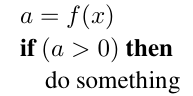
在这里，函数\(f\)可能返回“丑陋”的值，比如\(\infty\)或\(\mathrm{NaN}\)。对于\(\mathrm{NaN}\)和\(-\infty\)来说，\(if\)语句里的表达式会为假。而对于\(+\infty\)来说，会为真。

效率问题（Efficiency）

  对于让代码更加有效率来说没有什么魔法规则，效率是通过谨慎地衡量实现的。对于可见的未来来说一个良好的启发是，对于编程者来说，相比于操作次数应该更加关心内存访问方式。这和20几年前的想法是不一样的，因为内存速度没有跟上处理器的速度的发展。正是因为这样，有限且一致的内存访问对于优化只会越来越重要。
  让代码更快的一个合理方法是采用如下的步骤：

1. 以尽可能最直接的方式编写代码，在运行中直接计算中间值而不是存储它们。

2. 以优化模式编译代码。

3. 使用任何性能分析工具来找到最重要的性能瓶颈。

4. 检查数据结构来找到更好的方式提升局部性，如果可能的话，让数据单元的大小匹配上目标架构上的缓存或页的大小。

5. 如果性能分析揭示在数值计算方面有瓶颈，可以检查编译器生成的汇编代码，来找到效率低的地方。接着重写源代码来解决你找到的任何问题。

最重要的也就是第一个步骤，作者也说明了KISS即keep it simple,stupid的准则，大多数优化会让代码更难阅读，而没有速度上的提升。此外，最好把时间更多地投入到修复BUG以及增加新的特性上。最后还要注意下有些老的技巧可能不管用了，因为众所周知的是处理器在各种方面正在变得越来越快速。在所有情况下，对于特定机器或编译器的优化都需要进行性能分析，以确定优化是否有价值。

设计和编写图形程序（Designing and Coding Graphics Programs）

  对于设计和编写图形程序来说，有些常用的策略。这个部分将提供一些或许对你有帮助的建议。

类设计（Class Design）

  图形程序中的一个关键部分是对图形实体和几何实体有良好的类和函数设计。这些函数应该尽可能的简单且高效。对于设计来说，有个问题是位置和位移是否应该在分开的类，因为它们有不同的运算。对于位置来说，乘以\(0.5\)会显得没意义，而对于位移来说却有。抛开这种有争议的类设计，一些基础的类应该包括

• 二维向量（vector2）：存储x、y分量，此外应该还要支持加、减、点乘、叉乘等基础操作。

• 三维向量（vector3）：和二维向量类相似，不过多了一个z分量

• 齐次向量（hvector）：比三维向量多了个齐次坐标w

• RGB颜色（rgb）：RGB颜色存储三个分量，应该支持加、减、乘等操作

• 变换（transform）：应该包括4x4的用于变换的矩阵，还应该支持与矩阵和向量相乘的操作

• 图像（image）：带有输出操作的RGB像素的二维数组。

单精度VS双精度（Float vs. Double）

  现代架构倾向于通过降低内存使用以及保持连续的内存访问来提高效率，这就意味着使用单精度浮点数。然而，有时为了避免数值问题，会使用双精度浮点数。比如现在想要生成一张分形的图像，如下图所示。当放大倍率过高时，会超出单精度浮点数的精度极限，这个时候使用双精度浮点数可以良好地解决这一问题。

调试图形程序（Debugging Graphics Programs）

  以下是在计算机图形学中的一些特别有用的调试策略。

科学探究方法（The Scientific Method）

  在图形程序中，有一种有用的传统调试的替代方法。当我们创建图像并观察当中的错误时，这个时候必须提出一种为什么导致这个问题的猜想，并且进行测试。以光线追踪程序为例，有时候可能会看到一些很暗的像素。这是大多数人在写光线追踪器会遇到的一个经典的叫阴影痤疮（shadow acne）的问题。传统的调试在这里不起作用，我们应该意识到阴影光线击中了正在被着色的表面，所以看到的暗像素实际上是环境光颜色，正是因为自遮蔽的发生导致了直接光照的缺失。所以你可能假设被着色的位置被错误地判断为在阴影中，为了测试这个假设可以关闭阴影检测，在重新编译后进行验证。

把图像作为调试输出（Images as Coded Debugging Output）

  在很多情况下，获得调试信息的方法就是输出图像本身。如果想知道对于每个像素的计算的某个部分的变量，可以修改程序，直接把值输出到图像。打个比方就是，如果猜测着色的问题是由表面法线引起的，这个时候可以直接输出法线到图像。

使用一个调试器（Using a Debugger）

  有时使用科学探究方法会很难。比如当看不出来到底发生了什么时。图形程序可能涉及非常多的相同代码的执行，使得单步调试变得很难。而且最难的BUG通常只发生在复杂的输入时。
  一个有用的方法是为BUG“设置一个陷阱”。首先确保以单线程运行程序，并且让随机数的种子固定。接着找到是哪个像素或三角形出现了问题，如果发现是像素\((126,247)\)出现了问题，那么可以在代码前面添加

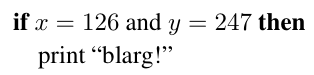
通过在print语句这里下断点，就能调试出问题的地方。有一些调试器有“条件断点”，使用它无需修改代码。
  当程序崩溃时，传统的调试器会定位崩溃的地方，接着，你应该在程序中使用断言和重新编译来回溯，找到出错的地方。这些断言应该留在程序中，为了那些在未来会遇到的潜在BUG。

数据可视化调试（Data Visualization for Debugging）

  有时，很难理解你的程序做了什么。因为直到出错前，程序会计算很多中间结果。在这种时候，可以采用更好的方式来说明计算的过程做了什么，比如对于光线追踪器来说可以写代码来可视化光线树，从而查看哪些路径对当前像素的值有贡献。这样能更好地理解计算机做了什么，而且还有利于代码优化。