改进版梯度下降
发展历史
标准梯度下降法的缺陷
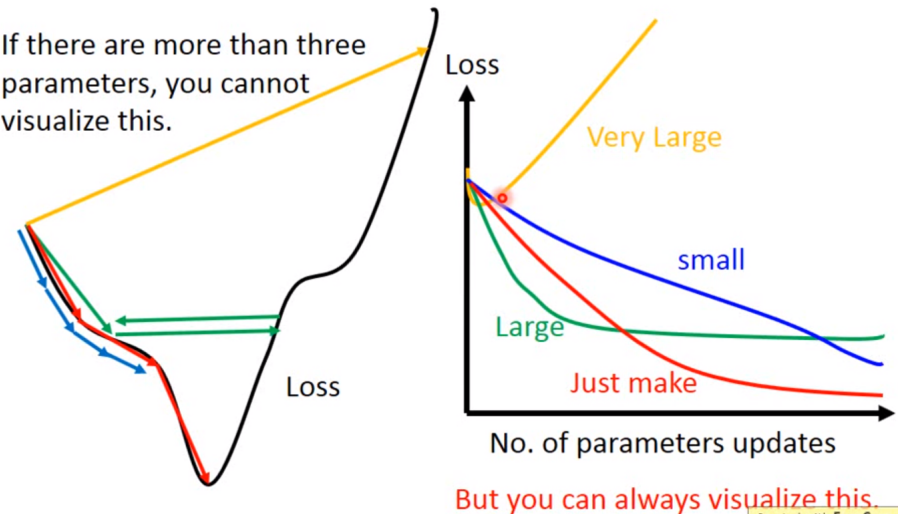
如果学习率选的不恰当会出现以上情况
因此有一些自动调学习率的方法。一般来说，随着迭代次数的增加，学习率应该越来越小，因为迭代次数增加后，得到的解应该比较靠近最优解，所以要缩小步长η，那么有什么公式吗？比如：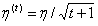
，但是这样做后，所有参数更新时仍都采用同一个学习率，即学习率不能适应所有的参数更新。
解决方案是：给不同的参数不同的学习率
Adagrad法
假设N元函数f(x)，针对一个自变量研究Adagrad梯度下降的迭代过程，
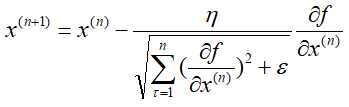
可以看出，Adagrad算法中有自适应调整梯度的意味（adaptive gradient），学习率需要除以一个东西，这个东西就是前n次迭代过程中偏导数的平方和再加一个常量最后开根号。
举例：使用Adagrad算法求y = x2的最小值点
导函数为g(x) = 2x
初始化x(0) = 4，学习率η=0.25，ε=0.1
第①次迭代：
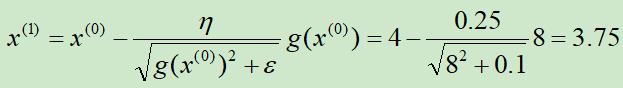
第②次迭代：
第③次迭代：
求解的过程如下图所示
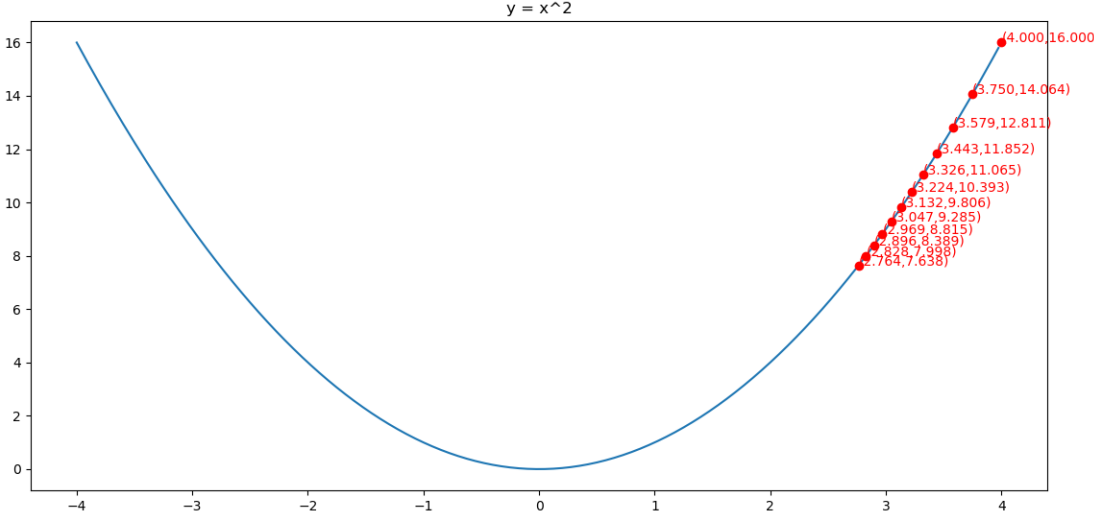
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() x = np.arange(-4, 4, 0.025) plt.plot(x,x**2) plt.title("y = x^2") def f(x): return x**2 def h(x): return 2*x η = 0.25 ε = 0.1 x = 4 iters = 0 sum_square_grad = 0 X = [] Y = [] while iters<12: iters+=1 X.append(x) Y.append(f(x)) sum_square_grad += h(x)**2 x = x - η/np.sqrt(sum_square_grad+ε)*h(x) print(iters,x) plt.plot(X,Y,"ro") ax = plt.subplot() for i in range(len(X)): ax.text(X[i], (X[i])**2, "({:.3f},{:.3f})".format(X[i], (X[i])**2), color='red') plt.show()
RMSprop法
AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。为了解决这一问题，RMSprop算法对Adagrad算法做了一点小小的修改，RMSprop使用了加权平均的方法,由累积平方梯度变成平均平方梯度,解决了后期学习率太小的缺点.(类似于动量梯度下降)
假设N元函数f(x)，针对一个自变量研究RMSprop梯度下降的迭代过程，
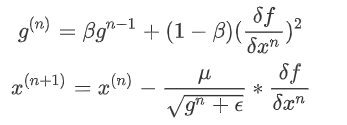
可以看出分母不再是一味的增加，它会重点考虑距离他较近的梯度（指数衰减的效果），也就不会出现Adagrad到后期收敛缓慢的问题
举例：使用RMSprop算法求y = x2的最小值点
导函数为h(x) = 2x
初始化g(0) = 1，x(0) = 4，ρ=0.9，η=0.01，ε=10-10
第①次迭代：
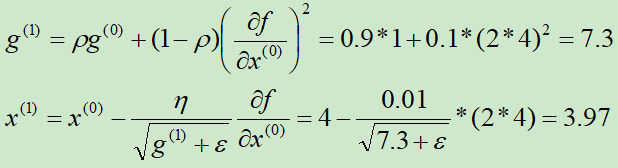
第②次迭代：
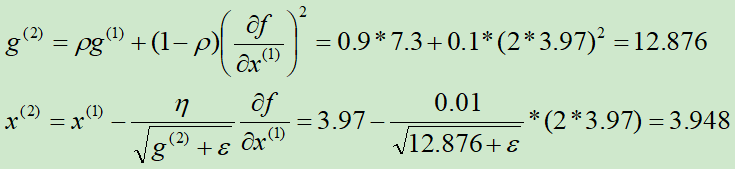
求解的过程如下图所示
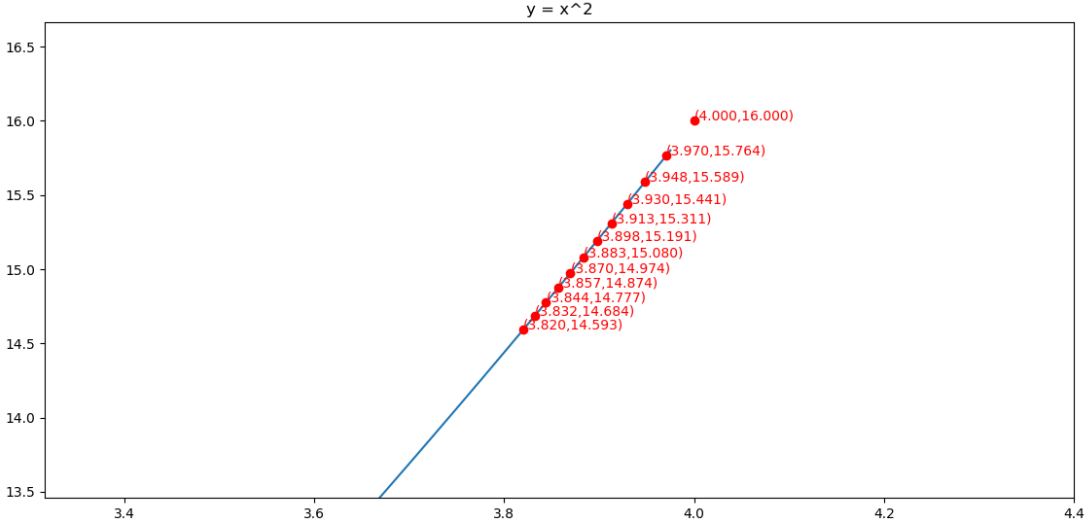
对应代码为：
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() x = np.arange(-4, 4, 0.025) plt.plot(x,x**2) plt.title("y = x^2") def f(x): return x**2 def h(x): return 2*x g = 1 x = 4 ρ = 0.9 η = 0.01 ε = 10e-10 iters = 0 X = [] Y = [] while iters<12: iters+=1 X.append(x) Y.append(f(x)) g = ρ*g+(1-ρ)*h(x)**2 x = x - η/np.sqrt(g+ε)*h(x) print(iters,x) plt.plot(X,Y,"ro") ax = plt.subplot() for i in range(len(X)): ax.text(X[i], (X[i])**2, "({:.3f},{:.3f})".format(X[i], (X[i])**2), color='red') plt.show()
Momentum是动量的意思，想象一下，一个小车从高坡上冲下来，他不会停在最低点，因为他还有一个动量，还会向前冲，甚至可以冲过一些小的山丘，如果面对的是较大的坡，他可能爬不上去，最终又会倒车回来，折叠几次，停在谷底。
如果使用的是没有动量的梯度下降法，则可能会停到第一个次优解
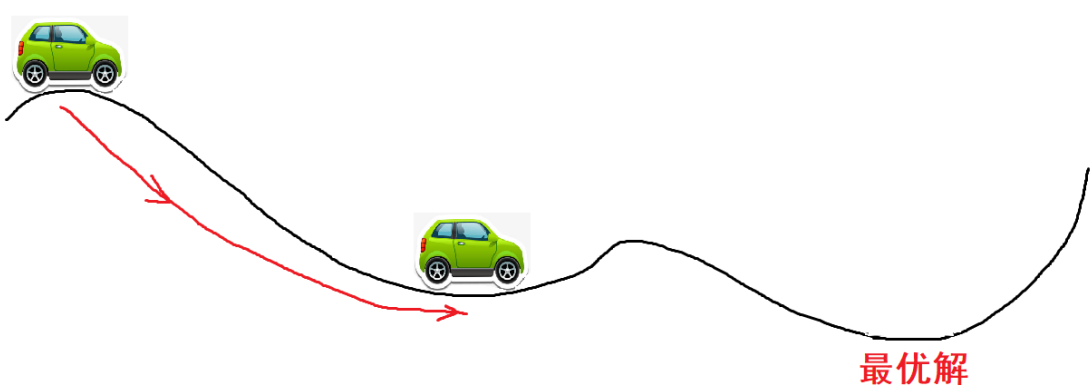
最直观的理解就是，若当前的梯度方向与累积的历史梯度方向一致，则当前的梯度会被加强，从而这一步下降的幅度更大。若当前的梯度方向与累积的梯度方向不一致，则会减弱当前下降的梯度幅度。
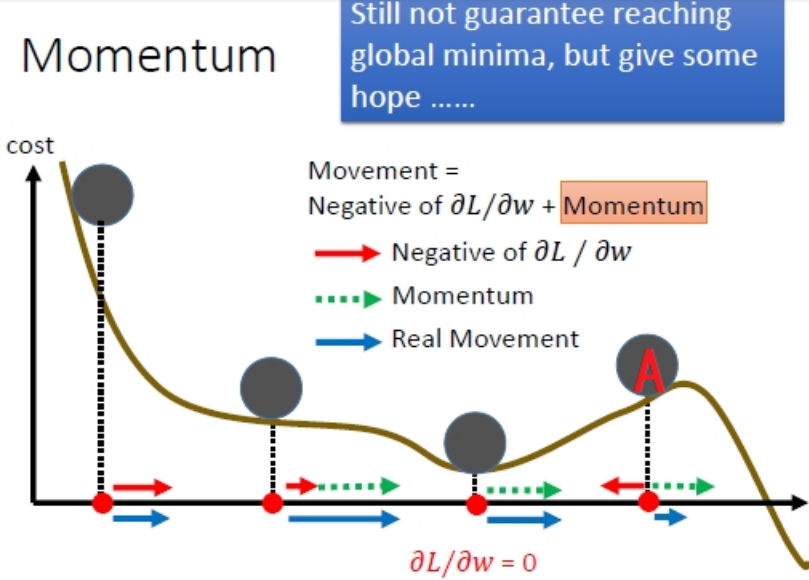
从这幅图可以看出来，当小球到达A点处，负梯度方向的红箭头朝着x轴负向，但是动量方向（绿箭头）朝着x轴的正向并且长度大于红箭头，因此小球在A处还会朝着x轴正向移动。
下面正式介绍Momentum法
假设N元函数f(x)，针对一个自变量研究Momentum梯度下降的迭代过程，
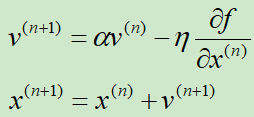
v表示动量，初始v=0
α是一个接近于1的数，一般设置为0.9，也就是把之前的动量缩减到0.9倍
η是学习率
下面通过一个例子演示一下，求y = 2*x^4-x^3-x^2的极小值点
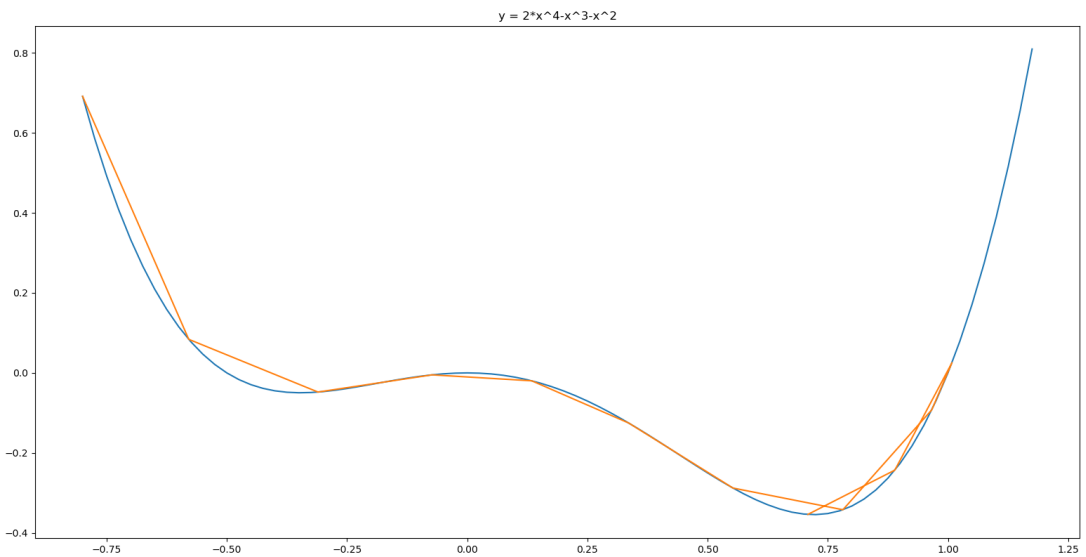
可以看出从-0.8开始迭代，依靠动量成功越过第一个次优解，发现无法越过最优解，折叠回来，最终收敛到最优解。对应代码如下:
from matplotlib import pyplot as plt import numpy as np fig = plt.figure() x = np.arange(-0.8, 1.2, 0.025) plt.plot(x,-x**3-x**2+2*x**4) plt.title("y = 2*x^4-x^3-x^2") def f(x): return 2*x**4-x**3-x**2 def h(x): return 8*x**3 - 3*x**2 - 2*x η = 0.05 α = 0.9 v = 0 x = -0.8 iters = 0 X = [] Y = [] while iters<12: iters+=1 X.append(x) Y.append(f(x)) v = α*v - η*h(x) x = x + v print(iters,x) plt.plot(X,Y) plt.show()
Adam法
假设N元函数f(x)，针对一个自变量研究Adam梯度下降的迭代过程，
下面依次解释这五个式子：
在②式中，借鉴的是RMSprop的指数衰减
③和④式目的是纠正偏差
⑤式进行梯度更新
举例：使用Adagrad算法求y = x2的最小值点
导函数为h(x) = 2x
初始化x(0) = 4，m(0) = 0，v(0) = 0，β1=0.9，β2=0.999，ε=10-8，η = 0.001
第①次迭代：
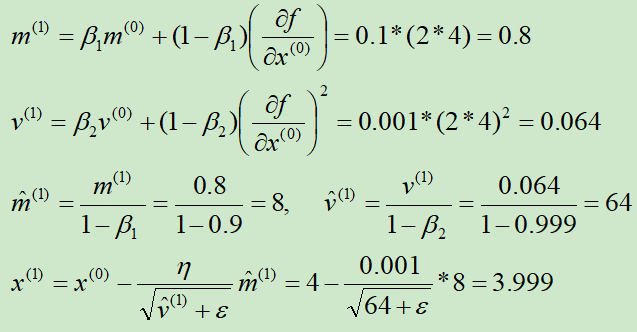
第②次迭代：
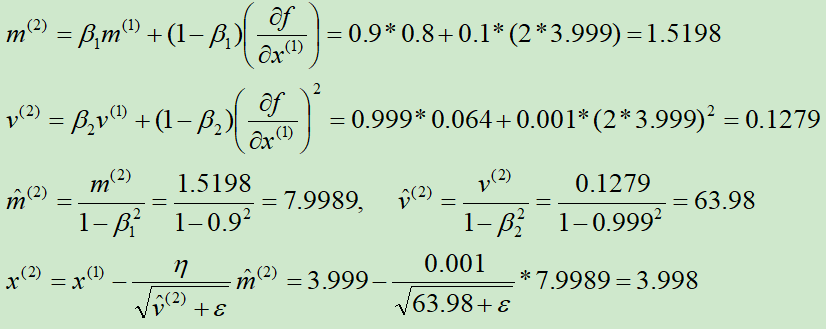
求解的过程如下图所示:
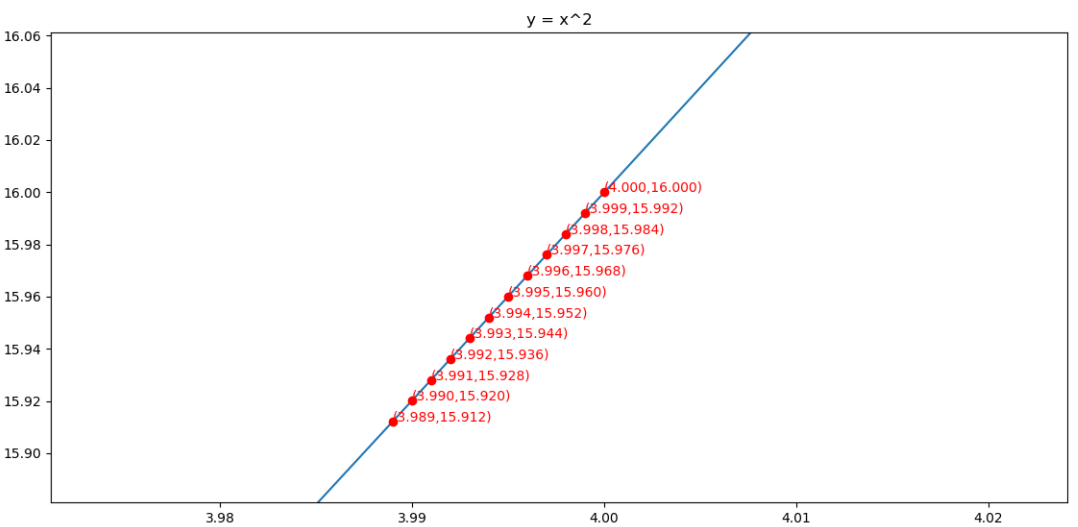
对应代码为：
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() x = np.arange(-4, 4, 0.025) plt.plot(x,x**2) plt.title("y = x^2") def f(x): return x**2 def h(x): return 2*x x = 4 m = 0 v = 0 β1 = 0.9 β2 = 0.999 η = 0.001 ε = 10e-8 iters = 0 X = [] Y = [] while iters<12: iters+=1 X.append(x) Y.append(f(x)) m = β1*m + (1-β1)*h(x) v = β2*v + (1-β2)*h(x)**2 m_het = m/(1-β1**iters) v_het = v/(1-β2**iters) x = x - η/np.sqrt(v_het+ε)*m_het print(iters,x) plt.plot(X,Y,"ro") ax = plt.subplot() for i in range(len(X)): ax.text(X[i], (X[i])**2, "({:.3f},{:.3f})".format(X[i], (X[i])**2), color='red') plt.show()
