深度分析-梯度下降
梯度下降
由于梯度下降法中负梯度方向作为变量的变化方向,所以有可能导 致最终求解的值是局部最优解,所以在使用梯度下降的时候,一般需 要进行一些调优策略: 学习率的选择:
- 学习率过大,表示每次迭代更新的时候变化比较大,有可能 会跳过最优解;
- 学习率过小,表示每次迭代更新的时候变化比较小,就会导 致迭代速度过慢,很长时间都不能结束;
算法初始参数值的选择:
- 初始值不同,最终获得的最小值也有可能不同,因为梯度下降法求解的是局部最优解,所以一般情况下,选择多次不同初始值 运行算法,并最终返回损失函数最小情况下的结果值;
标准化:由于样本不同特征的取值范围不同,可能会导致在各个不同参数上 迭代速度不同,为了减少特征取值的影响,可以将特征进行标准化操作。
梯度下降二维案例
import numpy as np import matplotlib.pyplot as plt import matplotlib as mpl mpl.rcParams['font.sans-serif'] = [u'simHei'] mpl.rcParams['axes.unicode_minus'] = False def f(x): return 0.5*(x-0.25)**2 def h(x): return x-1/4 X = [] Y = [] x =2 # 此时的学习率,是由一定区间的,过小会导致性能变慢,过大可能发散 step = 0.8 f_change = f(x) f_current = f(x) X.append(x) Y.append(f_current) # 当变化值小于1e-10的时候停止,也就是梯度 while f_change > 1e-10 and len(X)<100: # 这里是梯度下降的变化程度x = x - k*f(x)' x = x - step * h(x) tmp = f(x) f_change = np.abs(f_current - tmp) f_current = tmp X.append(x) Y.append(f_current) fig = plt.figure() X2 = np.arange(-2.1,2.65,0.05) Y2 = 0.5*(X2-0.25)**2 plt.plot(X2,Y2,'-',color="#666666",linewidth = 2) plt.plot(X,Y,'bo--') plt.title("$y= 0.5*(x-0.25)^2$通过梯度下降法得到目标值x=%.2f,y=%.2f迭代次数%d"%(x,f_current,len(X))) plt.show()
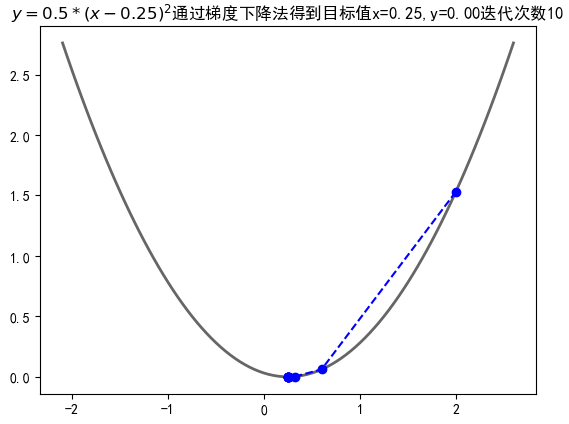
梯度下降三维案例
import numpy as np import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D def f(x, y): return x ** 2 + y ** 2 def h(t): return 2 * t X = [] Y = [] Z = [] x = 2 y = 2 f_change = x ** 2 + y ** 2 f_current = f(x, y) step = 0.1 X.append(x) Y.append(y) Z.append(f_current) while f_change > 1e-10: # 对于各自未知数求偏导 x = x - step * h(x) y = y - step * h(y) f_change = np.abs(f_current - f(x,y)) f_current = f(x,y) X.append(x) Y.append(y) Z.append(f_current) fig = plt.figure() ax = Axes3D(fig) X2 = np.arange(-2,2,0.2) Y2 = np.arange(-2,2,0.2) X2,Y2 = np.meshgrid(X2,Y2) Z2 = X2**2 + Y2**2 ax.plot_surface(X2,Y2,Z2,rstride=1,cstride=1,cmap='rainbow') ax.plot(X,Y,Z,'ro--') ax.set_title("") plt.show()
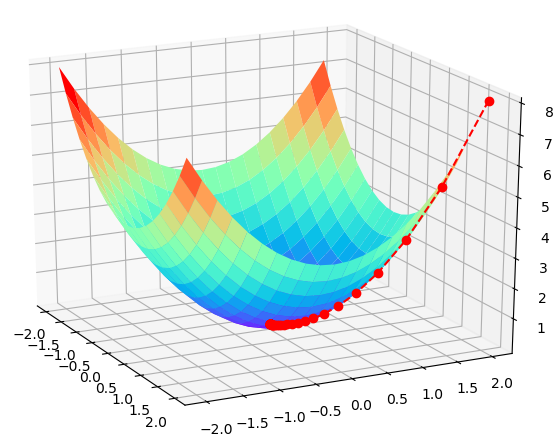
再机器学习中梯度算法简直是一个利刃,能够帮助我们求解很多参数
分析解题步骤
目标函数θ求解 初始化θ(随机初始化,可以初始为0) 沿着负梯度方向迭代,更新后的θ使J(θ)更小
![]()
![]()
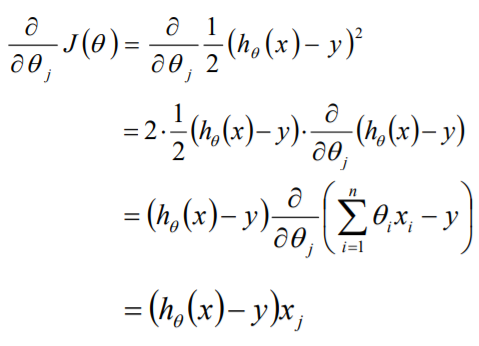
梯度下降研究每次迭代N个数
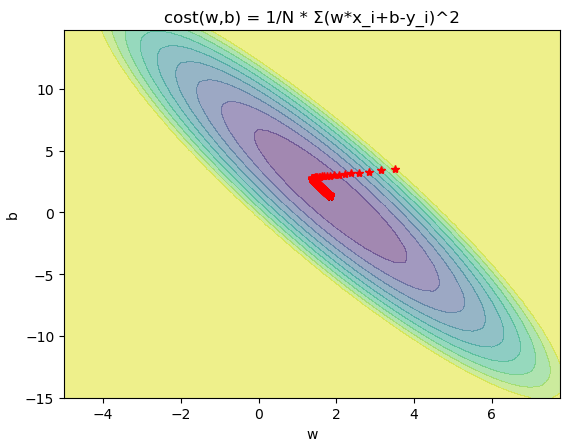
BGD
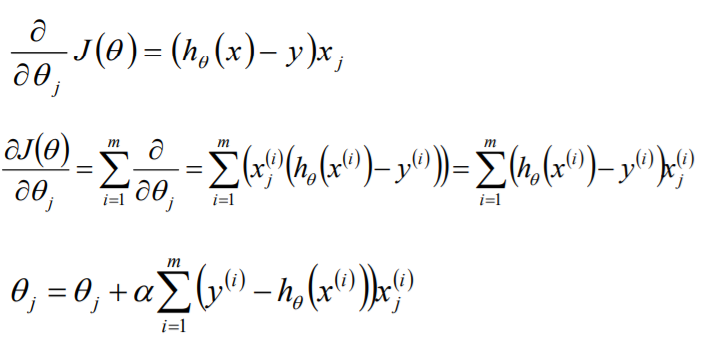
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() w = np.arange(-5, 8, .25) b = np.arange(-15, 15, .25) x = np.array([1,2,3,4]) y = np.array([3.2,4.7,7.3,8.5]) w, b = np.meshgrid(w, b) R = 0 for i in range(len(x)): R += (w*x[i]+b-y[i])**2 R /= len(x) a = R<50 R = ~a*50+R*a ax = plt.subplot() plt.contourf(w, b, R,10,alpha=0.5) plt.title("cost(w,b) = 1/N * Σ(w*x_i+b-y_i)^2") w = 3.5 b = 3.5 W = [] B = [] for i in range(2000): W.append(w) B.append(b) w -= 0.02*1/len(x)*sum((w*x+b-y)*x) b -= 0.02*1/len(x)*sum((w*x+b-y)) print(w,b) plt.plot(W,B,"r*") plt.xlabel("w") plt.ylabel("b") plt.show()
SGD
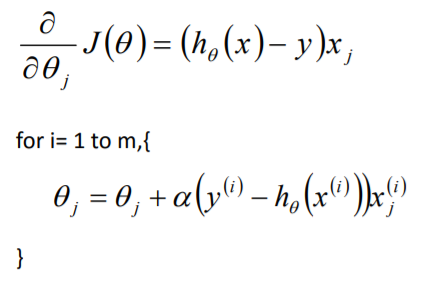
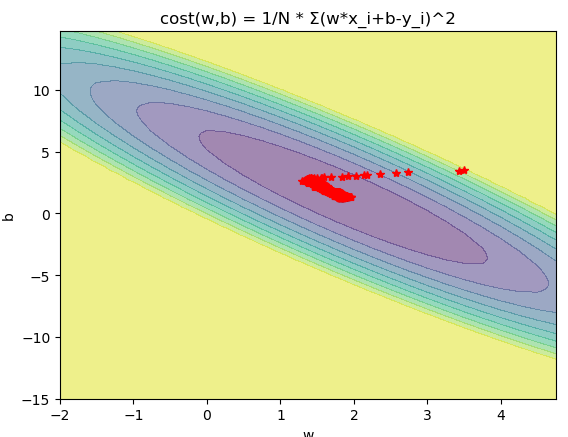
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D import random fig = plt.figure() w = np.arange(-2, 5, .25) b = np.arange(-15, 15, .25) x = np.array([1,2,3,4]) y = np.array([3.2,4.7,7.3,8.5]) w, b = np.meshgrid(w, b) R = 0 for i in range(len(x)): R += (w*x[i]+b-y[i])**2 R /= len(x) a = R<50 R = ~a*50+R*a ax = plt.subplot() plt.contourf(w, b, R,10,alpha=0.5) plt.title("cost(w,b) = 1/N * Σ(w*x_i+b-y_i)^2") w = 3.5 b = 3.5 W = [] B = [] for i in range(2000): W.append(w) B.append(b) p = random.randint(0, len(x)-1) w -= 0.02*(w*x[p]+b-y[p])*x[p] b -= 0.02*(w*x[p]+b-y[p]) print(w,b) plt.plot(W,B,"r*") plt.xlabel("w") plt.ylabel("b") plt.show()
- SGD速度比BGD快(迭代次数少)
- SGD在某些情况下(全局存在多个相对最优解/J(θ)不是一个二次),SGD有可能跳 出某些小的局部最优解,所以不会比BGD坏
- BGD一定能够得到一个局部最优解(在线性回归模型中一定是得到一个全局最优 解),SGD由于随机性的存在可能导致最终结果比BGD的差
- 注意:优先选择SGD
MBGD
如果即需要保证算法的训练过程比较快,又需要保证最终参数训练的准确率,而 这正是小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)的初 衷。MBGD中不是每拿一个样本就更新一次梯度,而且拿b个样本(b一般为10)的 平均梯度作为更新方向。

BGD、SGD、MBGD的区别:
- 当样本量为m的时候,每次迭代BGD算法中对于参数值更新一次,SGD算法 中对于参数值更新m次,MBGD算法中对于参数值更新m/n次,相对来讲 SGD算法的更新速度最快;
- SGD算法中对于每个样本都需要更新参数值,当样本值不太正常的时候,就 有可能会导致本次的参数更新会产生相反的影响,也就是说SGD算法的结果 并不是完全收敛的,而是在收敛结果处波动的;
- SGD算法是每个样本都更新一次参数值,所以SGD算法特别适合样本数据量 大的情况以及在线机器学习(Online ML)。
三个概念
导数反映的是函数y=f(x)在某一点处沿x轴正方向的变化率。
比如y=x2,在x=1处的导数=2。
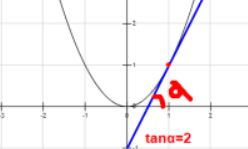
导数是通过极限来定义的,某一点的导数=tanψ,但是前提是△x趋近于0,此时tanψ=tanα=该点导数,公式如下:

![]()
偏导
在多元函数中,偏导数指的是函数y(x1,x2,…,xn)沿某一坐标轴(x1,x2,…,xn)正方向的变化率。
![]()
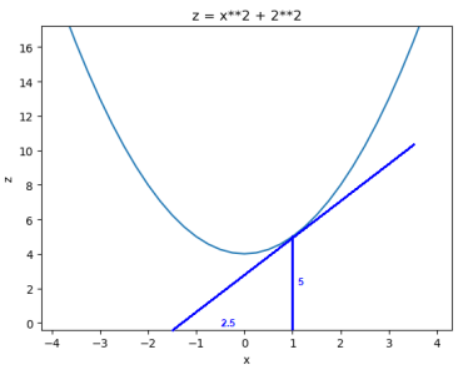
比如![]() ,在(1,2)处的在x方向上的偏导数:
,在(1,2)处的在x方向上的偏导数:![]()

截取y=2的曲线,可以发现在x方向的导数=2
导数和偏导数都是沿坐标轴正方向的变化率。那么当我们讨论函数沿任意方向的变化率时,也就引出了方向导数的定义,即:某一点在某一趋近方向上的导数值。
比如,可以计算函数在点A(2,2,8)的导数。

梯度
梯度是一个向量,表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。
![]()
比如z=x2+y2+xy在点A(2,2,12)处的梯度为
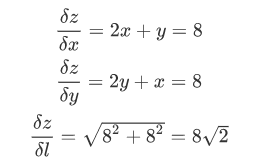
对所有的参数更新使用同样的学习率。对于稀疏数据或者特征,有时我们可能想更新快一些对于不经常出现的特征,对于常出现的特征更新慢一些,这时候SGD就不太能满足要求了
3.SGD容易收敛到局部最优
最直观的理解就是,若当前的梯度方向与累积的历史梯度方向一致,则当前的梯度会被加强,从而这一步下降的幅度更大。若当前的梯度方向与累积的梯度方向不一致,则会减弱当前下降的梯度幅度。
其中,μ是动量因子
- 下降初期,使用上一次参数更新,下降方向一致则乘上较大的μ能够进行很好的加速
- 下降中后期时,在局部最小值来回震荡的时候,gradient→0,μ使得更新幅度增大,跳出局部最优解
- 在梯度改变方向的时候,μ能够减少更新
总而言之,momentum项能够在相关方向加速SGD,抑制振荡,从而加快收敛。
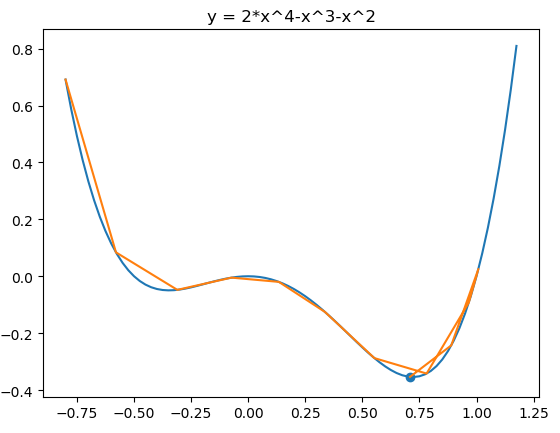
代码:
from matplotlib import pyplot as plt import numpy as np fig = plt.figure() x = np.arange(-0.8, 1.2, 0.025) plt.plot(x,2*x**4-x**3-x**2) plt.title("y = 2*x^4-x^3-x^2") def f(x): return 2*x**4-x**3-x**2 def h(x): return 8*x**3 - 3*x**2 - 2*x η = 0.05 α = 0.9 v = 0 x = -0.8 iters = 0 X = [] Y = [] while iters<12: iters+=1 X.append(x) Y.append(f(x)) v = α*v - η*h(x) x = x + v print(iters,x) plt.plot(X,Y) plt.scatter(X[-1],Y[-1]) plt.show()
Adagrad法
Adagrad其实是对学习率进行了一个约束。即: 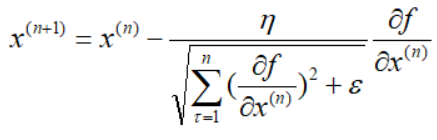
特点:
- 前期根号下的值较小的时候, 学习率较大,能够放大梯度
- 后期根号下的值较大的时候,学习率较小,能够约束梯度
- 适合处理稀疏梯度
缺点:
- 公式上可以看出,仍依赖于人工设置一个全局学习率η设置过大整个式子过于敏感,对梯度的调节太大
- 中后期,分母上梯度平方的累加将会越来越大,使gradient→0,训练过慢。
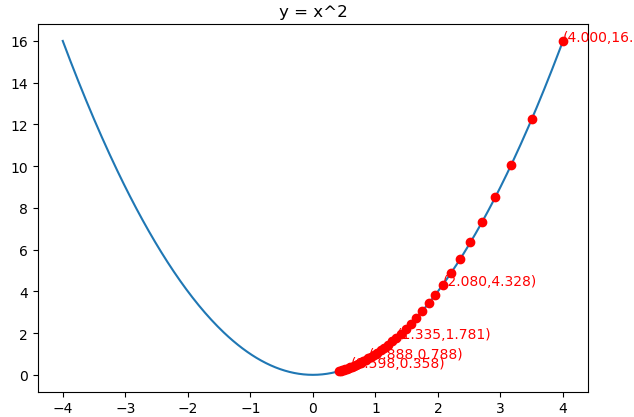
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() x = np.arange(-4, 4, 0.025) plt.plot(x,x**2) plt.title("y = x^2") def f(x): return x**2 def h(x): return 2*x η = 0.5 ε = 0.1 x = 4 iters = 0 sum_square_grad = 0 X = [] Y = [] while iters<40: iters+=1 X.append(x) Y.append(f(x)) sum_square_grad += h(x)**2 x = x - η/np.sqrt(sum_square_grad+ε)*h(x) print(iters,x) plt.plot(X,Y,"ro") ax = plt.subplot() for i in range(len(X)): if i%8==0: ax.text(X[i], (X[i])**2, "({:.3f},{:.3f})".format(X[i], (X[i])**2), color='red') plt.show()
RMSprop
当β等于0.5的时候,g再求根的话就变成了求RMSE(均方根)
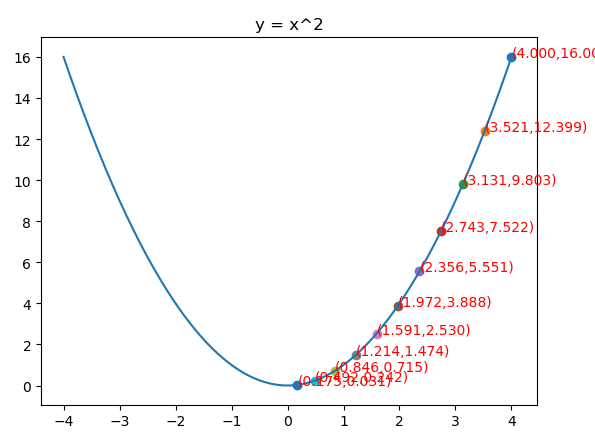
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() x = np.arange(-4, 4, 0.025) plt.plot(x,x**2) plt.title("y = x^2") def f(x): return x**2 def h(x): return 2*x g = 1 x = 4 ρ = 0.9 η = 0.01 ε = 10e-10 iters = 0 X = [] Y = [] while iters<420: iters+=1 X.append(x) Y.append(f(x)) g = ρ*g+(1-ρ)*h(x)**2 x = x - η/np.sqrt(g+ε)*h(x) print(iters,x) ax = plt.subplot() for i in range(len(X)): if i % 40==0: plt.scatter(X[i], Y[i]) ax.text(X[i], (X[i])**2, "({:.3f},{:.3f})".format(X[i], (X[i])**2), color='red') plt.show()
优点:
- RMSprop依然依赖于全局学习率
- RMSprop算是Adagrad的变体,效果趋于二者之间
- 适合处理非平稳目标
- 对于RNN效果很好
Adam实际上是把momentum和RMSprop结合起来的一种算法也就是带有动量项的RMSprop
假设N元函数f(x),针对一个自变量研究Adam梯度下降的迭代过程,

优点:
- 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
- 对内存需求较小
- 为不同的参数计算不同的自适应学习率
- 也适用于大多非凸优化
- 适用于大数据集和高维空间
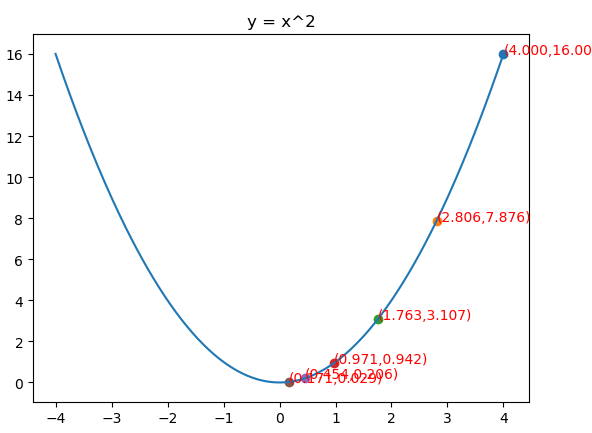
from matplotlib import pyplot as plt import numpy as np from mpl_toolkits.mplot3d import Axes3D fig = plt.figure() x = np.arange(-4, 4, 0.025) plt.plot(x,x**2) plt.title("y = x^2") def f(x): return x**2 def h(x): return 2*x x = 4 m = 0 v = 0 β1 = 0.9 β2 = 0.999 η = 0.061 ε = 10e-8 iters = 0 X = [] Y = [] while iters<120: iters+=1 X.append(x) Y.append(f(x)) m = β1*m + (1-β1)*h(x) v = β2*v + (1-β2)*h(x)**2 m_het = m/(1-β1**iters) v_het = v/(1-β2**iters) x = x - η/np.sqrt(v_het+ε)*m_het print(iters,x) ax = plt.subplot() for i in range(len(X)): if i %20==0: plt.scatter(X[i],Y[i],) ax.text(X[i], (X[i])**2, "({:.3f},{:.3f})".format(X[i], (X[i])**2), color='red') plt.show()


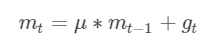
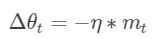
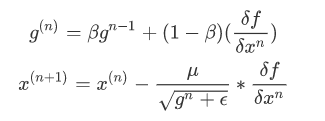

 浙公网安备 33010602011771号
浙公网安备 33010602011771号