后缀数组

后缀数组

定义

\(sa_i\) 表示排名为 \(i\) 的后缀起点下标。

\(rk_i\) 表示后缀 \(i\) 的排名。

求 SA

\(O(n\log^2 n)\) 的基本思路是倍增。

假设已知 \(i\) 开头长为 \(l\) 的串的排名为 \(rk_i\)，只需要根据 \(rk_i\) 和 \(rk_{i+l}\) 进行双关键字排序就能得到 \(i\) 开头长为 \(2l\) 的串的排名。每一次长度能倍增。最后得到每一个位置开头，长度为 \(l>n\) 的串的排名，相当于后缀的排名。

使用 sort 直接进行双关键字排序可以做到 \(O(n\log^{2}n)\)，使用基数排序可以优化至 \(O(n\log n)\)。

有几个小优化，优化较为明显。首先按照第二关键字排序，对于开头在 \([n-l+1,n]\) 的串，它们的 \(i+l\) 超过了 \(n\)，所以第二关键字为 \(0\)，按照第二关键字排序之后一定在最前面。剩下的部分，若 \(sa_i>w\)，则插入 \(sa_i-w\) 这个位置。也就是说由于上次已经对第二关键字的所有串排序了，直接插入即可。

实现有一些技巧，可以看看 OI-Wiki 上的代码。

height 数组

下文中 \(lcp(i,j)\) 表示后缀 \(i\) 和后缀 \(j\) 的最长公共前缀。

\(height_{i}\) 定义为 \(lcp(sa_i,sa_{i-1})\)。

引理：\(height[rk_i]\ge height[rk_{i-1}]-1\)。人话：后缀 \(i\) 与其前一名的最长公共前缀长度 至少 为 \(i-1\) 后缀与其前一名的最长公共前缀长度减一。

证明：

若 \(height[rk_{i-1}]\le 1\)，则右边不超过 \(0\)，显然成立。

否则，如图：

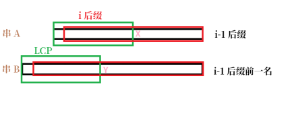
绿色部分即为 \(i-1\) 后缀 \(height[rk_{i-1}]\)，由定义知，绿色部分后一个字符 \(X>Y\)。

\(A\) 串红色部分 \(i\) 后缀。由于 \(X>Y\)，故 \(B\) 串红色部分字典序必小于 \(A\) 串红色部分。

若 \(B\) 红为 \(A\) 红前一名，引理成立。否则考虑中间夹着的串，容易发现，引理仍成立。

故求 \(height\) 数组可以 \(O(n)\)，具体地，利用引理暴力求，由于每一次只会减一，总共只能减 \(n\) 次，也就只能加 \(O(n)\) 次了。