第一次作业：深度学习基础

第一次作业：深度学习基础

0x00 人工智能和机器学习概述

人工智能(Artificial Intelligence)，使一部机器相认一样进行感知、认知、决策、执行的人工程序或系统。

人工智能历史

1956 达特茅斯会议标志AI诞生

1957 罗森布拉特发明感知机

1960 通用问题求解系统GPS系统

1968 DENDRAL专家系统问世

1969 M.Minsky和S.Papert指出感知机的局限性+本身技术条件的限制联结主义陷入谷底

1983 J.Jhop field解决NP难问题，使得连结主义重新受到人们关注

20世纪80年代 符号足以的代表方法是决策树和基于逻辑的学习

1986 D.E.Rumel-hart等人发明了BP算法

20世纪90年代 统计学习登场，并迅速占领了历史舞台，代表性技术是SVM

2006 Hlnton提出了深度学习的神经网络

人工智能的三个层面

计算智能：能存能算

感知智能：能听会说、能看会认

认知智能：能理解，会思考

逻辑演绎vs归纳总结

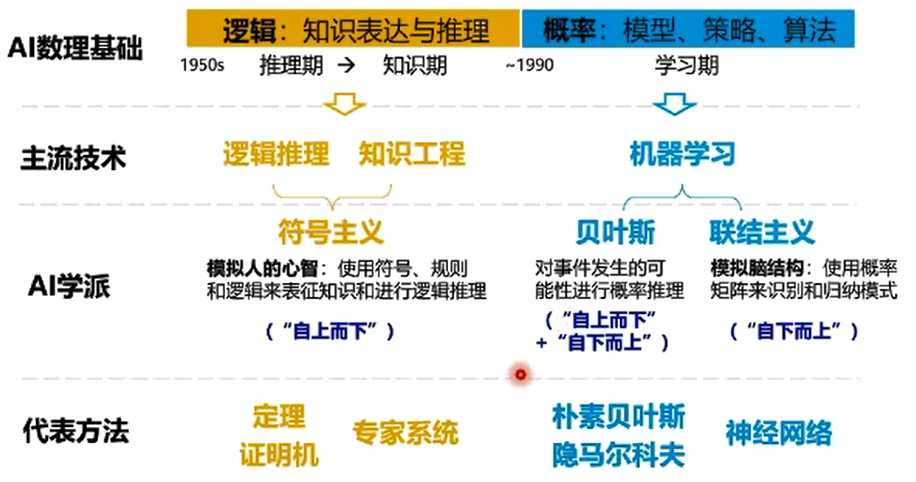
image-20211002123011133

知识工程/专家系统 根据专家定义的知识和经验，进行推理和判断，从而模拟人类专家的决策过程来解决问题

  • 基于手工设计规则建立专家系统
  • 结果容易理解
  • 系统构建费时费力
  • 依赖专家主观静安，难以保证一致性和准确性

机器学习 机器自动训练

  • 基于数据自动学习

  • 减少人工繁杂工作，但结果可能不易解释

  • 提高信息处理的效率，且准确率较高

  • 来源于真实数据，减少人工规则主观性，可信度高

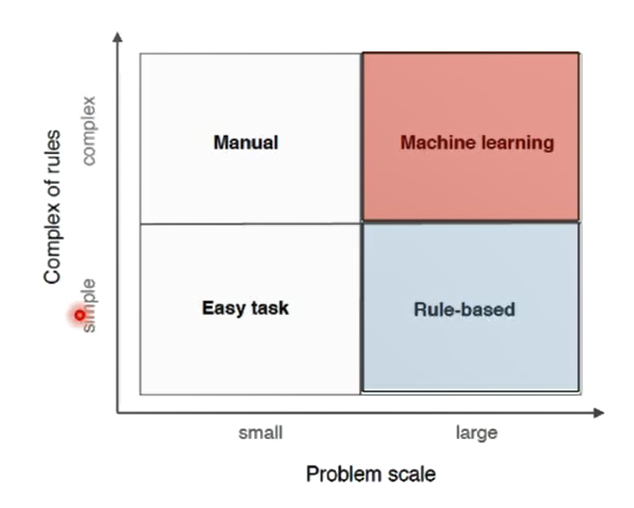
image-20211002123932460

0x01机器学习

定义

最常用定义：计算机系统能够利用经验提高自身的性能

可操作定义：机器学习本质是一个基于经验数据的函数估计问题

统计学定义：提取重要模式、趋势，并理解数据，即从数据中学习

怎么学

模型：对要学习问题映射的假设（问题建模，确定假设空间）

策略：从假设空间中学习/选择最优模型的准则（确定目标函数）

算法：根据目标函数求解最优模型的具体计算方法（求解模型参数）

分类
数据标记：监督学习vs无监督学习

无监督学习从数据中学习模式，适用于描述数据

监督学习从数据中学习标记分界面（输入-输出的映射函数），适用于预测数据标记

半监督学习：部分数据标记已知，监督学习和无监督学习的混合

强化学习：数据标记未知，但知道与输出目标相关的反馈，决策类问题

数据分布：参数vs无参数模型

参数模型：对数据进行假设，待求解的数据模式/映射可以用一组有限且固定数目的参数进行刻画

例：线性回归、逻辑回归、感知机、k均值聚类

非参数模型：不对数据分布进行假设，数据的所有统计特征都来源于数据本身

例：k近邻模型、SVM、决策树、随机森林

tips:

  • 非参≠无参，“参数”指数据分布的参数，而不是模型的参数。非参数模型的时空复杂度一般比参数模型大得多

  • 参数模型的模型参数固定，非参数模型是自适应数据的，模型参数随样本的变化而变化

建模对象：判别vs生成模型

生成模型：对输入X和输出Y的联合分布P(X, Y)建模

例：朴素贝叶斯、隐马尔科夫、马尔科夫随机场

优点：

  • 提供更多信息（建模边缘分布->采样生成样本）
  • 样本量大时，更快收敛到真实分布
  • 支持复杂训练情况（无监督训练、存在隐变量时）

缺点：

  • 数据需求大
  • 预测类问题准确率通常不如判别模型

判别模型：对已知输入X的条件下输出Y的条件分布P(Y|X)建模

例：SVM、逻辑回归、条件随机场、决策树

0x02深度学习概述

传统机器学习vs深度学习

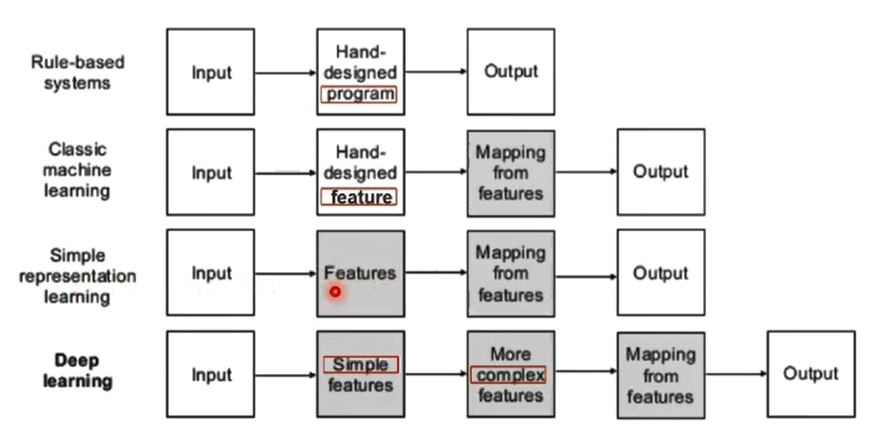
image-20211002132338569

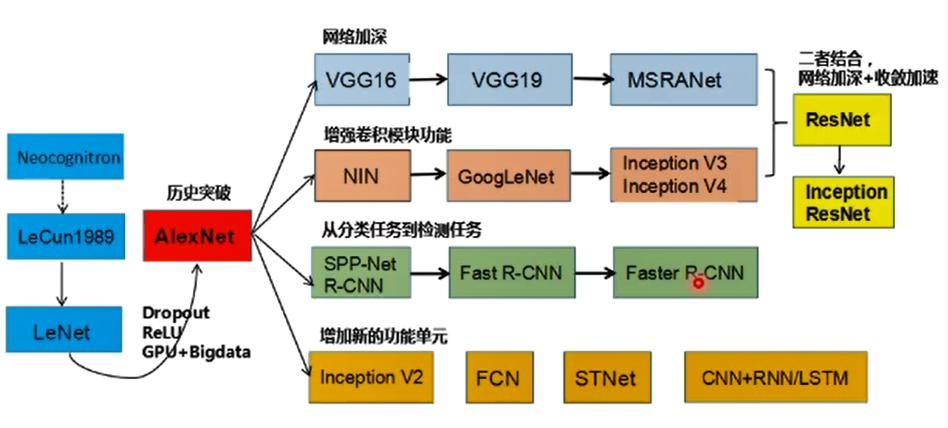
神经网络结构的发展

image-20211002134752650

深度学习的“不能”
  • 算法输出不稳定，容易被“攻击”
  • 模型复杂度高，难以纠错和调试
  • 模型层级复合程度高，参数不透明
  • 端到端训练方式对数据依赖性强，模型增量性差
  • 专注直观感知类问题，对开放性问题推理能力无能为力
  • 人类只是无法有效引入进行监督，机器偏见难以避免

0x03神经网络基础

生物神经元
  • 每个神经元都是一个多输入单输出的信息处理单元
  • 神经元具有空间整合和时间整合特性
  • 神经元输入分兴奋性输入和抑制性输入两种
  • 神经元具有阈值特性
M-P神经元
  • 多输入信号进行累加
  • 权值\(w_i\)正负模拟兴奋/抑制，大小模拟强度
  • 输入和超过阈值\(\theta\)​，神经元被激活（fire）
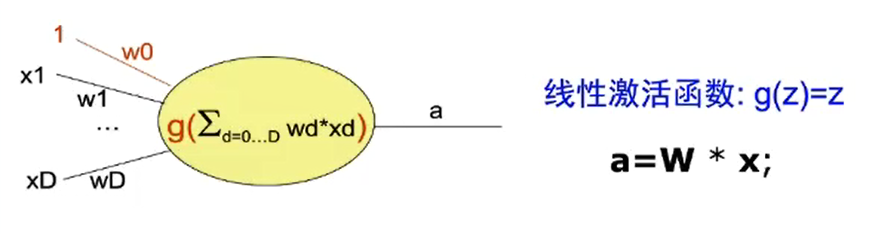
激活函数f

神经元继续传递信息、产生新连接的概率（超过阈值被激活，但不一定传递）

没有激活函数相当于矩阵相乘，多层和一层一样，只能拟合线性函数

例：

  • 线性函数

    \(f(x) = k * x + c\)

  • 斜面函数

    \(f(x) = \begin{cases} &T, & x \ge c \\ &k*x, &|x|\leq c \\ &-T, &x \lt -c \\ \end{cases}\)

  • 阈值函数（e.g.阶跃函数）

    \(f(x)=\begin{cases} &1, &x \ge c \\ &0, &x \lt c \\ \end{cases}\)​

  • 符号函数

    \(y = F(x) = \begin{cases}&1, &x \gt 0 \\ &2, &x \le 0\end{cases}\)

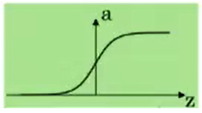
  • Sigmoid函数

    \(\sigma(z) = \frac {1}{1+e^{-z}}\)

    \(\sigma(z)^{'} = \sigma(z)(1-\sigma(z))\)​

    image-20211002205627614

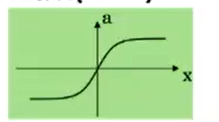
  • tanh函数

    \(\displaystyle tanh(x)=2sigmoid(2x)-1=\frac {e^z-e^{-z}} {e^z+e^{-z}}\)

    \(g(z)^{'}=1-g(z)^2\)

    image-20211002205636215

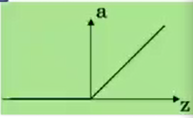
  • ReLU

    \(relu(z) = max(0,z)\)

    image-20211002210627389

  • Leaky ReLU

    \(leakyrelu(z)=max(0.01z, z)\)

单层感知器

M-P神经元的权重预先设置，无法学习

单层感知器是首个可以学习的人工神经网络

image-20211002210901967

多层感知器

解决了单层感知机不能解决非线性可分问题的问题

万有逼近定理

如果一个隐层包含足够多的神经元，三层前馈神经网络（输入-隐层-输出）能以任意精度逼近任意预定的连续函数

双隐层感知机逼近非连续函数

当隐层足够宽时，双隐层感知器（输入-隐层1-隐层2-输出）可以逼近任意非连续函数：可以解决任何复杂的分类问题。

神将网络每一层的作用
  • 神经网络学习如何利用矩阵的线性变换加激活函数的非线性变换，将原始输入空间投影到线性可分的空间去分类/回归。
  • 增加节点数：增加维度，即增加线性转换能力。
  • 增加层数：增加激活函数的次数，即增加非线性转换次数。
更宽or更深？

  • 在神经元总数相当的情况下，增加网络深度可以比增加宽度带来更强的网络表示能力：产生更多的线性区域

  • 深度和宽度对函数复杂度的贡献是不同的，深度的贡献是指数增长的，而宽度的贡献是线性的。

    \(FC=\prod\limits ^d_{l=1}(\alpha · \theta)^{\beta_l}\)

    其中\(\alpha\)表示参数每层对函数复杂度的贡献，\(\theta\)表示参数数量，\(\beta\)表示深度对函数复杂度的贡献，\(\alpha\)和\(\beta\)都是一个区间即相同的参数在不同数值下仍然有不同的复杂度。\(d\)表示最大深度，\(l\)表示第\(l\)层。

神经网络的参数学习：误差反向传播

  • 多层神经网络可看成一个复合的非线性多元函数\(F(·)：X\to Y\)

    \(F(x)=f_n(...f_3(f_2(f_1(x)*\theta_1+b)*\theta_2+b)...)\)

    给定训练数据\(\{x^i,y^i\}_{i=1:N}\)，希望损失\(\sum_iloss(F(x^i),y^i)\)​尽可能小

    image-20211002214151158

梯度和梯度下降

梯度：

  • 多元函数\(f(x,y)\)在每个点可以有多个方向
  • 每个方向都可以计算导数，称为方向导数
  • 梯度是一个向量
    • 方向是最大方向导数的方向
    • 模为方向导数的最大值
无约束优化：梯度下降

参数沿负梯度方向更新可以使函数值下降

\(\theta_j=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta)\)​

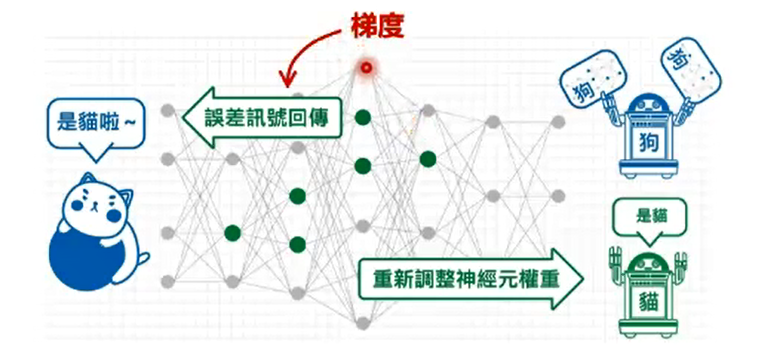
误差反向传播

复合函数的链式求导

image-20211002214851865

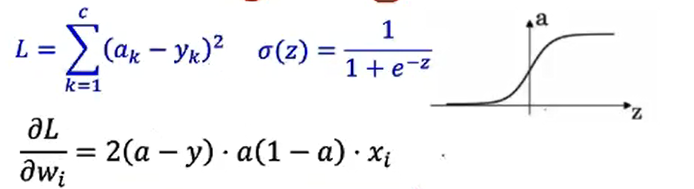
image-20211002220825221

梯度消失
  • 增加深度会造成梯度消失（gradient vanishing），误差无法传播
  • 多层网络容易陷入局部极值，难以训练
逐层预训练
受限玻尔兹曼机和自编码器
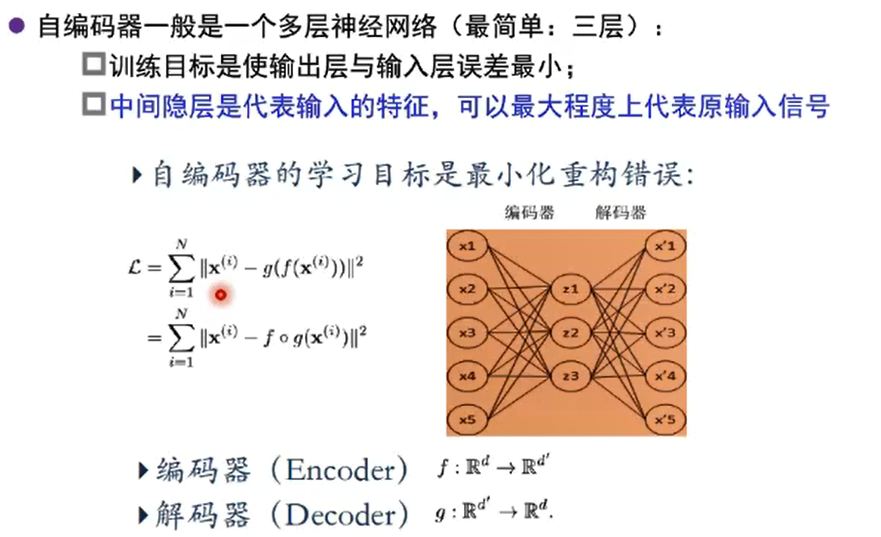
自编码器（autoencoder）

假设输入与输出相同（target=input），是一种尽可能复现输入信号的神经网络

将Input输入一个encoder编码器，就会得到一个code，加一个decoder解码器，输出信息。

通过调整encoder和decoder的参数，使得重构误差最小

没有额外监督信息:无标签数据，误差的来源是直接重构后信息与源输入相比得到

image-20211002222527426

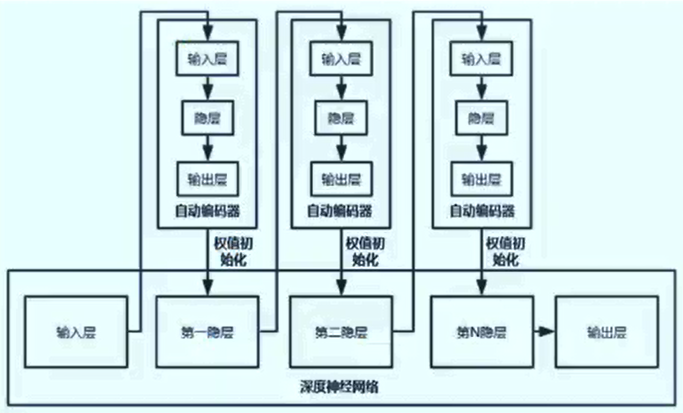
堆叠自编码器（stack autoencoder, SAE）

  • 将多个自编码器得到的隐层串联
  • 所有层预训练完成后，进行基于监督学习的全网络微调

image-20211002222659575

  • 数据输入\((x_1,x_1),(x_2,x_2),...,(x_N,x_N)\)
  • 期望回归函数为\((x,x)\)，实际学到的回归函数\((x, F(x))\)
  • 其中\(F(x)=S(W^{2r}(x)^{2r})=(x)^{2r+1}\)（r层编码，r层解码）
  • 一般编码层每层结点数递减，解码层每层的节点数递增（可用于降维）
  • 自编码器是一种网络结构，可**配合其他结构搭建深度网络（如卷积、池化等）
  • 根据经验风险最小化策略，应最小化的目标函数为\(|I-F|=\prod^N_{k=1}||x_k-F(x_k)||^2\)
  • 可使用BP算法求解
受限玻尔兹曼机（RBM）

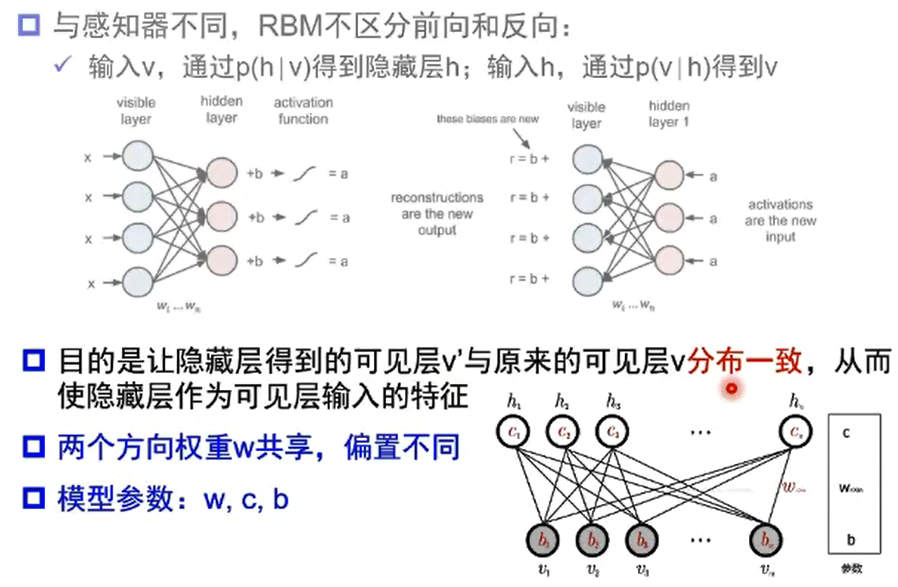
image-20211002223412904

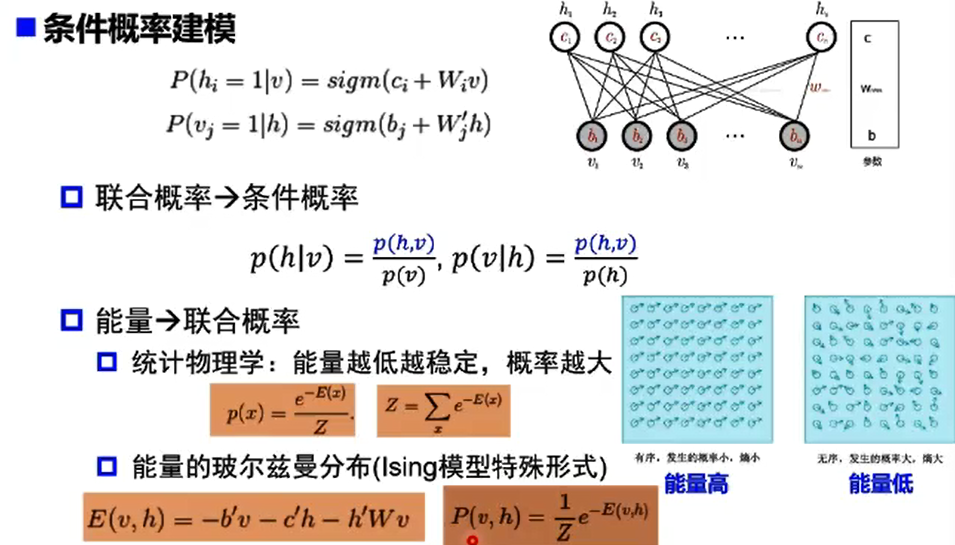
image-20211002223617844

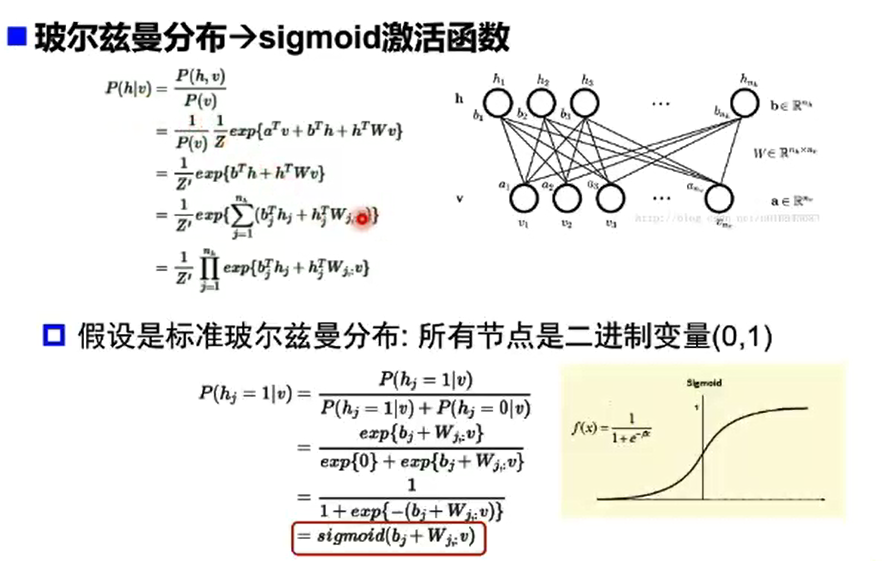
image-20211002223635660

image-20211002223723444

image-20211002223743421

image-20211002223824005

image-20211002223854721

自编码器vs受限玻尔兹曼机
  • 结构上
    • 自编码器编码和解码函数不同：W1, W2
    • RBM共享权重矩阵，两个偏置向量
  • 原理上
    • 自编码器通过非线性变换学习特征，是确定的，特征值可以为任何实数；
    • RBM基于概率分布定义，高层表示为底层特征的条件概率，输出只有两种状态（未激活/激活），用二进制0/1表示
  • 训练优化
    • 自编码器通过最损失函数L最小化重构输入数据，直接用BP优化求解
    • RBM基于最大似然，能量函数偏导无法直接计算，基于采样方法进行估计
  • 生成/判别模型
    • RBM对联合概率密度建模，是生成式模型
    • 自编码器直接对条件概率建模，是判别式模型
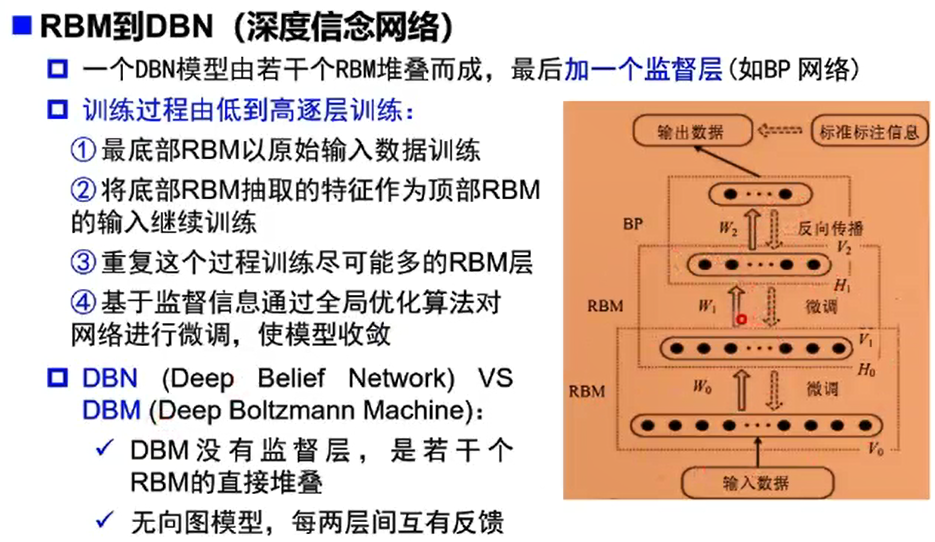
DNN vs DBN
  • DNN是前馈神经网络，训练方法是BP
  • 隐层激活函数使用ReLU\(\to\)改善梯度消失
  • 输出层激活函数是softmax，目标函数是交叉熵+大量标注数据\(\to\)避免差的局部极小值
  • 正则化+dropout\(\to\)改善过拟合
  • 没有使用逐层预训练
解决梯度消失
  • Layer-wise Pre-train：2006年Hinton等提出的训练深度网络的方法，用无监督数据作分层预训练，再用有监督数据fine-tune
  • ReLU：新的激活函数解析性质更好，克服了sigmoid函数和tanh函数的梯度消失问题
  • 辅助损失函数：e.g. GoogLeNet中的两个辅助损失函数，对浅层神经元直接传递梯度
  • Batch Normalization：逐层的尺度归一
  • LSTM：通过选择记忆和遗忘机制克服RNN的梯度消失问题，从而可以建模长时序列

0x04总结

人工智能是一个广阔的概念，机器学习是其中的一个方面，而深度学习是机器学习的一个方面。

神经网络仿照生物的神经元，由M-P神经元出现开始，到单层感知器（首个可以学习的人工网络），再到多层感知器和激活函数（解决了非线性可分问题），BP方法调整参数可以使loss函数向极小值靠近，再到ReLU函数改善梯度下降，直到今天的AlexNet、Inception家族、ResNet及一些变种。中间由于理论或硬件技术等难题经历过几次低谷，随着技术的发展和理论的更新，有过几次爆发。

当今的人工智能还在感知智能的方面发展（视觉、自然语言处理等），仍存在着很多不足和难以解决的问题。

问题
  1. 对于一些原理只知道了内容，但并不知道是怎么来的。比如：万有逼近定理。
  2. 激活函数相当于对原数据空间进行了一次空间变换？为什么这样的空间变换能够保证得到的结果一定线性可分？感觉比较模糊，不大理解。
  3. 受限玻尔兹曼机和自编码器基本上都没听懂。
posted @ 2021-10-03 01:07  小渔村x  阅读(301)  评论(0)    收藏  举报