一种低于根号 n 复杂度的块状链表

部分图片来自OI wiki

由于条件原因，部分图片可能略显粗糙，望轻喷。

我知道这是平凡的，但是我写这篇文章仅仅是因为没有人写过而已。

前置知识

块状链表，相信大家都会。

引入

众所周知，块状链表是一种形如下图的结构。

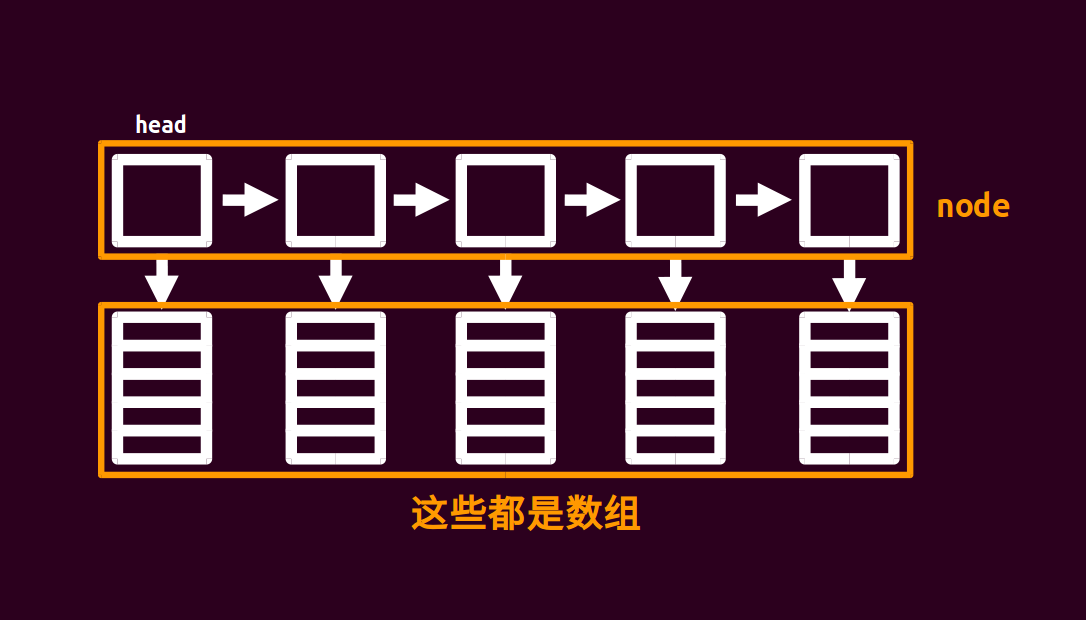
它通过遍历外层链表一次，来找到查询位置对应的位置，再遍历内层数组统计贡献。两个遍历的复杂度均为 \(O(n^\frac{1}{2})\)，因此单次操作复杂度为 \(O(n^\frac{1}{2})\)。

但是 \(O(n^\frac{1}{2})\) 的复杂度还是太高了，一旦遇到 \(n=10^6\) 的情况就很难跑过实际上常数小，基本不会被卡。有没有办法降低它的复杂度呢？

算法原理

事实上是有的。我们要降低复杂度，就要降低数组长度。降低数组长度就需要多加维度才能维护所有信息。

为了实现这一目标，我们将普通块状链表的内层数组换成块状链表，即块状链表套块状链表。这样就会形成下图所示的结构：

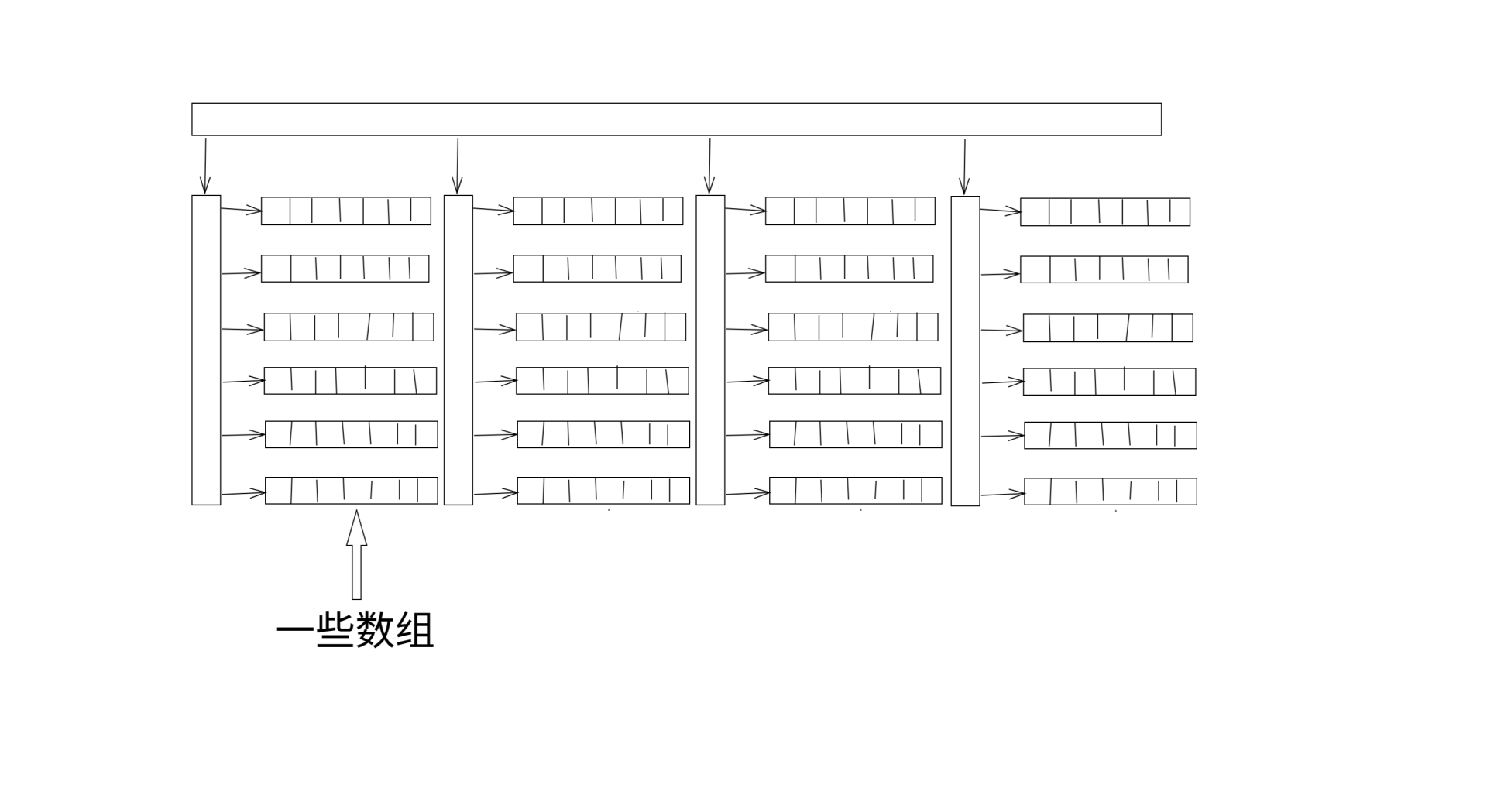
我们令块长为 \(len\)，那么我们每次只要遍历三次长为 \(len\) 的链表或数组就可以查询任意一个数。单次操作复杂度 \(O(\frac{n}{len^2}+len)\)，当 \(len=n^\frac{1}{3}\) 时达到理论最优复杂度 \(O(n^\frac{1}{3})\)。内层块状链表最多重构 \(O(\frac{n}{len})\) 次，每次重构复杂度 \(O(len)\)。外层块状链表最多重构 \(O(\frac{n}{len^2})\) 次，每次重构复杂度 \(O(len^2)\)，重构总复杂度 \(O(n)\)。

实际上，这样的块状链表可以无限制地套下去。套越多的块状链表，时间复杂度就越低，同时实现难度和常数也会相应升高。由于笔者码力有限，并没有实现过套 \(\ge 3\) 层的块状链表，但目测常数会很大，没有实现的必要。

实现细节

外层块状链表在内层链表长度达到 \(2\times len\) 时暴力重构，内层同普通块状链表。

例题

由于实际功能与普通块状链表相同，只是复杂度上的优化，因此不给出过多例题。（实际上用途并不大）

P6136 【模板】普通平衡树（数据加强版）

块状链表板子，支持查询排名即可。

提交记录

#include <bits/stdc++.h>
using namespace std;
constexpr int N=1e6+6,len=104,nel=105;
int n,m,a[nel][(len<<1)|1][(len<<1)|1],nxt[nel][(len<<1)|1],cnt[nel],maxn[nel];
int res[len*len*4+1],top;
void insert(int pos,int val){
    for(int i=1;i;i=nxt[i][0]){
        if(pos<=a[i][0][0]+1){
            if(pos==a[i][0][0]+1)maxn[i]=val;
            for(int j=1;j;j=nxt[i][j]){
                if(pos<=a[i][j][0]+1){
                    memmove(a[i][j]+pos+1,a[i][j]+pos,(a[i][j][0]-pos+1)<<2);
                    a[i][j][pos]=val;
                    a[i][j][0]++;
                    if(a[i][j][0]==len*2){ // 重构内层
                        memcpy(a[i][++cnt[i]]+1,a[i][j]+len+1,len<<2);
                        a[i][cnt[i]][0]=a[i][j][0]=len;
                        nxt[i][cnt[i]]=nxt[i][j];
                        nxt[i][j]=cnt[i];
                    }
                    break;
                }
                else pos-=a[i][j][0];
            }
            a[i][0][0]++;
            if(cnt[i]==len*2){ // 重构外层
                nxt[++cnt[0]][0]=nxt[i][0];
                nxt[i][0]=cnt[0];top=0;
                for(int j=1;j;j=nxt[i][j]){
                    for(int k=1;k<=a[i][j][0];k++){
                        res[++top]=a[i][j][k];
                    }
                }
                for(int j=1;j<=top/2;j++)a[i][(j-1)/len+1][(j-1)%len+1]=res[j];
                for(int j=1;j<=(top+1)/2;j++)a[cnt[0]][(j-1)/len+1][(j-1)%len+1]=res[j+top/2];
                cnt[i]=(top/2-1)/len+1;cnt[cnt[0]]=((top+1)/2-1)/len+1;
                a[i][0][0]=top/2;a[cnt[0]][0][0]=(top+1)/2;
                for(int j=1;j<cnt[i];j++)a[i][j][0]=len;a[i][cnt[i]][0]=top/2-(cnt[i]-1)*len;
                for(int j=1;j<cnt[cnt[0]];j++)a[cnt[0]][j][0]=len;a[cnt[0]][cnt[cnt[0]]][0]=(top+1)/2-(cnt[cnt[0]]-1)*len;
                for(int j=1;j<cnt[i];j++)nxt[i][j]=j+1;nxt[i][cnt[i]]=0;
                for(int j=1;j<cnt[cnt[0]];j++)nxt[cnt[0]][j]=j+1;nxt[cnt[0]][cnt[cnt[0]]]=0;
                maxn[i]=res[top/2];maxn[cnt[0]]=res[top];
            }
            break;
        }
        else pos-=a[i][0][0];
    }
}
void erase(int pos){
    for(int i=1;i;i=nxt[i][0]){
        if(pos<=a[i][0][0]){
            for(int j=1;j;j=nxt[i][j]){
                if(pos<=a[i][j][0]){
                    memmove(a[i][j]+pos,a[i][j]+pos+1,(a[i][j][0]-pos+1)<<2);
                    a[i][j][0]--;
                    break;
                }
                else pos-=a[i][j][0];
            }
            a[i][0][0]--;
            break;
        }
        else pos-=a[i][0][0];
    }
}
int get_rank(int val){
    int rank=0;
    for(int i=1;i;i=nxt[i][0]){
        if(val<=maxn[i]){
            for(int j=1;j;j=nxt[i][j]){
                if(val<=a[i][j][a[i][j][0]]){
                    for(int k=1;k<=a[i][j][0];k++,rank++)if(a[i][j][k]>=val)break;
                    break;
                }
                else rank+=a[i][j][0];
            }
            break;
        }
        else rank+=a[i][0][0];
    }
    return rank;
}
int search(int pos){
    for(int i=1;i;i=nxt[i][0]){
        if(pos<=a[i][0][0]){
            for(int j=1;j;j=nxt[i][j]){
                if(pos<=a[i][j][0])return a[i][j][pos];
                else pos-=a[i][j][0];
            }
        }
        else pos-=a[i][0][0];
    }
    return -1;
}
int get_pre(int x){return search(get_rank(x));}
int get_nxt(int x){return search(get_rank(x+1)+1);}
void print(){
    for(int i=1;i;i=nxt[i][0]){
        for(int j=1;j;j=nxt[i][j]){
            for(int k=1;k<=a[i][j][0];k++){
                cout<<a[i][j][k]<<' ';
            }
        }
    }
    cout<<'\n';
}
int lastans,ans;
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    for(int i=0;i<nel;i++)cnt[i]=1;
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        int x;cin>>x;
        insert(get_rank(x)+1,x);
    }
    for(int i=1;i<=m;i++){
        int op,x;cin>>op>>x;x^=lastans;
        if(op==1)insert(get_rank(x)+1,x);
        if(op==2)erase(get_rank(x)+1);
        if(op==3)ans^=(lastans=get_rank(x)+1);
        if(op==4)ans^=(lastans=search(x));
        if(op==5)ans^=(lastans=get_pre(x));
        if(op==6)ans^=(lastans=get_nxt(x));
    }
    cout<<ans<<'\n';
    return 0;
}