题解:[集训队互测 2011] Crash 的文明世界
题意分析
树上问题
首先,\(n\) 个点 \(n-1\) 条边,显然是一个树。
因此,\(\operatorname{dist}(i,j)\) 其实可以 \(\mathcal O(1)\) 计算出来。只需要 \(\mathcal O(n\log n)\) 预处理一个 DFS 序 LCA 即可。(详见此处)
斯特林数
对于整数 \(x\) 的 \(k\) 次方,其实可以通过第二类斯特林数展开:
因此,\(S(u)\) 就可以转化为:
树型 DP
不难发现,关键便在于对于每一个点 \(u\),求出 \(\sum\limits_{v=1}^n\dbinom{\operatorname{dist}(u,v)}{i}\),且 \(0\leq i\leq k\)。
如果 \(u\) 确定,其实很简单,只需要 DFS 一遍即可。但是需要对于每一个点 \(u\) 都求一次,暴力 DFS 的复杂度是 \(\mathcal O\left(n^2\right)\) 的,无法接受。
不难发现,设边 \((x,y)\),且 \(x\) 为 \(y\) 的父节点,则将树根从 \(x\) 变为 \(y\) 是会且仅会影响 \(x,y\) 的答案的。因此考虑换根 DP。
第一次 DP
设 \(\textit{dp}_{x,i}\) 表示节点 \(x\) 的子树内,\(i=i\) 时的 \(\sum\limits_{y=1}^n\dbinom{\operatorname{dist}(x,y)}{i}\)。
记 \(\textit{son}_x\) 表示 \(x\) 的子节点集。
显然,有:
-
\(i=0\) 时,无论 \(\operatorname{dist}(x,y)\) 取何值,总有 \(\dbinom{\operatorname{dist}(x,y)}{0}=1\)。因此,\(\textit{dp}_{x,0}\) 就是 \(x\) 子树内节点个数,包括自己。
-
\(i\neq0\) 时,考虑组合数递推公式:
\[\dbinom{\operatorname{dist}(x,y)}{i}=\dbinom{\operatorname{dist}(x,y)-1}{i}+\dbinom{\operatorname{dist}(x,y)-1}{i-1} \]\(\operatorname{dist}(x,y)-1\),即对应从 \(y\) 开始。因为 \(y\) 对应的是 \(y\) 的子树中的贡献,\(x\) 走进去必然经过长度为 \(1\) 的 \((x,y)\)。
故,有:
\[\textit{dp}_{x,i}=\textit{dp}_{y,i}+\textit{dp}_{y,i-1} \]
换根 DP
设根节点 \(x\) 为 \(y\) 的父节点,已知 \(\textit{dp}_{x,i}\),推出 \(y\) 为根节点时的 \(\textit{dp}_{y,i}\)。
如图:
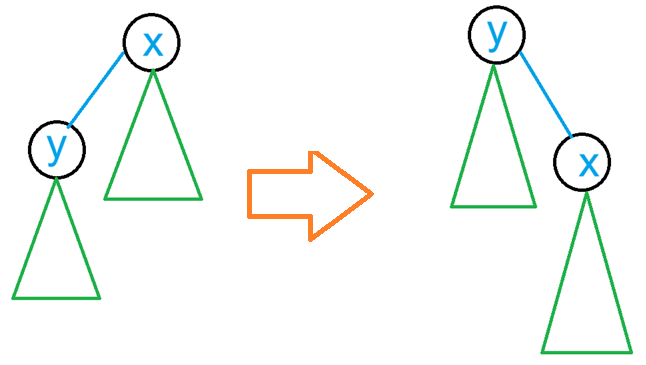
首先,要求出 \(x\) 作为根节点 \(y\) 的子节点时的子树内的 \(\textit{dp}'_{x,i}\)。
只需要减去 \(y\) 对 \(x\) 的贡献即可。
即:
这时,想求出根节点 \(y\) 的 \(\textit{dp}'_{y,i}\),只需要加上对应的 \(\textit{dp}'_{x,i}\) 即可:
这样,我们就将根节点从 \(x\) 换成了 \(y\),这时 \(\mathcal O(k)\) 统计答案即可。
AC 代码
注意答案非负。
时间复杂度:\(\mathcal O\left(n\log n+nk+n\right)\)。
其中,\(\mathcal O(nk)\) 是为了计算组合数、第二类斯特林数。
//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=5e4,K=150,P=10007;
int n,k,ans[N+1];
vector<int>g[N+1];
namespace base{
int dfn[N+1],order[N+1],dep[N+1],father[N+1],st[N+1][__lg(N+1)+1],reSt[N+1][__lg(N+1)+1];
void dfs(int x,int fx){
father[x]=fx;
dep[x]=dep[fx]+1;
static int cnt;
dfn[x]=++cnt;
order[dfn[x]]=x;
for(int i:g[x]){
if(i==fx){
continue;
}
dfs(i,x);
}
}
int qpow(int base,int n){
int ans=1;
while(n){
if(n&1){
ans=1ll*ans*base%P;
}
base=1ll*base*base%P;
n>>=1;
}
return ans;
}
int fact[K+1];
void pre(){
fact[0]=1;
for(int i=1;i<=K;i++){
fact[i]=1ll*fact[i-1]*i%P;
}
dfs(1,0);
for(int i=1;i<=n;i++){
st[i][0]=dep[order[i]];
reSt[i][0]=order[i];
}
for(int i=1;(1<<i)<=n;i++){
for(int x=1;x+(1<<i)-1<=n;x++){
if(st[x][i-1]<st[x+(1<<i-1)][i-1]){
st[x][i]=st[x][i-1];
reSt[x][i]=reSt[x][i-1];
}else{
st[x][i]=st[x+(1<<i-1)][i-1];
reSt[x][i]=reSt[x+(1<<i-1)][i-1];
}
}
}
}
int lca(int u,int v){
if(u==v){
return u;
}
if(dfn[u]>dfn[v]){
swap(u,v);
}
int s=__lg(dfn[v]-dfn[u]);
if(st[dfn[u]+1][s]<st[dfn[v]-(1<<s)+1][s]){
return father[reSt[dfn[u]+1][s]];
}else{
return father[reSt[dfn[v]-(1<<s)+1][s]];
}
}
int dist(int u,int v){
int lcaUV=lca(u,v);
return dep[u]+dep[v]-2*dep[lcaUV];
}
int C(int n,int m){
if(n<0||m<0||n<m){
return 0;
}
static int mem[N+1][K+1];
if(!m){
return 1;
}
if(mem[n][m]){
return mem[n][m];
}
return mem[n][m]=C(n-1,m)+C(n-1,m-1);
}
int Stirling2(int n,int k){
static int mem[K+1][K+1];
if(n<0||k<0||n<k){
return 0;
}
if(!k){
return !n;
}
if(mem[n][k]){
return mem[n][k];
}
return mem[n][k]=(Stirling2(n-1,k-1)+1ll*k*Stirling2(n-1,k)%P)%P;
}
}
namespace DP{
int dp[N+1][K+1];
void dfs0(int x,int fx){
dp[x][0]=1;
for(int y:g[x]){
if(y==fx){
continue;
}
dfs0(y,x);
dp[x][0]=(1ll*dp[x][0]+dp[y][0])%P;
for(int i=1;i<=k;i++){
dp[x][i]=(1ll*dp[x][i]+dp[y][i]+dp[y][i-1])%P;
}
}
}
void dfs1(int x,int fx){
for(int i=0;i<=k;i++){
ans[x]=(1ll*ans[x]+1ll*dp[x][i]*base::Stirling2(k,i)%P*base::fact[i]%P)%P;
if(ans[x]<0){
ans[x]+=P;
}
}
for(int y:g[x]){
if(y==fx){
continue;
}
dp[x][0]=(dp[x][0]-dp[y][0])%P;
for(int i=1;i<=k;i++){
dp[x][i]=(dp[x][i]-dp[y][i]-dp[y][i-1])%P;
}
dp[y][0]=(dp[y][0]+dp[x][0])%P;
for(int i=1;i<=k;i++){
dp[y][i]=(dp[y][i]+dp[x][i]+dp[x][i-1])%P;
}
dfs1(y,x);
dp[y][0]=(dp[y][0]-dp[x][0])%P;
for(int i=1;i<=k;i++){
dp[y][i]=(dp[y][i]-dp[x][i]-dp[x][i-1])%P;
}
dp[x][0]=(dp[x][0]+dp[y][0])%P;
for(int i=1;i<=k;i++){
dp[x][i]=(dp[x][i]+dp[y][i]+dp[y][i-1])%P;
}
}
}
int main(){
dfs0(1,0);
dfs1(1,0);
return 0;
}
}
int main(){
/*freopen("test.in","r",stdin);
freopen("test.out","w",stdout);*/
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin>>n>>k;
for(int i=1;i<n;i++){
int u,v;
cin>>u>>v;
g[u].push_back(v);
g[v].push_back(u);
}
base::pre();
DP::main();
for(int i=1;i<=n;i++){
cout<<ans[i]<<'\n';
}
cout.flush();
/*fclose(stdin);
fclose(stdout);*/
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号