树上最近公共祖先（LCA）问题

参考链接：OI Wiki

倍增LCA

倍增思想

可以参考ST表。

设 \(\large f_{x,i}\) 表示 \(x\) 的 \(2^i\) 级祖先，用 \(father_i\) 表示节点 \(i\) 的父节点，则显然：

\[\large f_{x,0}=father_x \]

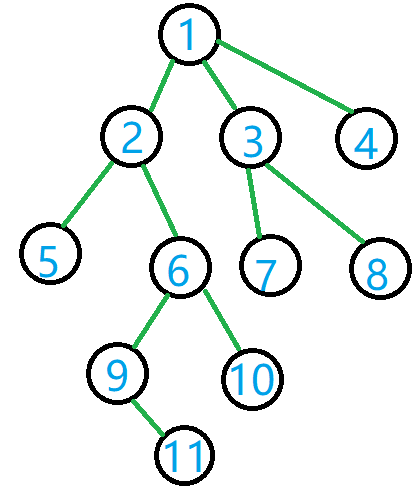
例如对于这棵树：

014

\(\large f_{9,0}=\normalsize father_9=6\)。
节点 \(9\) 的 \(2^1\) 级祖先 \(\large f_{9,1}=father_6=2\)。
节点 \(11\) 的 \(2^2\) 级祖先：

\[\begin{aligned}\large f_{11,2}&=\large 1\\\\&=\large f_{6,1}\\\\&=\large f_{f_{11,1},1}\end{aligned} \]

一个易于发现的事实是，节点 \(x\) 的 \(2^i\) 级祖先是其 \(2^{i-1}\) 级祖先的 \(2^{i-1}\) 级祖先。

那么状态转移方程为：

\[\Large f_{x,i}=f_{f_{x,i-1},i-1} \]

预处理

同ST表，代码很简单（\(f[x][i]\) 同上文 \(\large f_{x,i}\)）：

const int N=500000;
//邻接表
struct edge{
	int v,r;
}a[2*N+1];
//d:深度,h:链式前向星链头
int h[N+1],d[N+1],f[N+1][(int)log2(N)+1],lg[N+1];
//邻接表建边
void create(int u,int v){
	static int top=0;
	a[++top]={v,h[u]};
	h[u]=top;
}
//q:p的父节点 
void dfs(int p,int q){
	//基本信息 
	f[p][0]=q;//2^0=1,即p的父节点,q 
	d[p]=d[q]+1;//下一层 
	for(int i=h[p];i>0;i=a[i].r){
		if(a[i].v!=q)dfs(a[i].v,p);
	}
}
void lca_pre(){
	dfs(s,0);//s:树根
	for(int i=1;i<=n;i++)lg[i]=lg[i/2]+1;
	for(int i=1;i<=lg[n];i++){
		for(int x=1;x<=n;x++)f[x][i]=f[f[x][i-1]][i-1];
	}
}

时间复杂度：\(\mathcal O(n\log n)\)。

查询

为了便于查找节点 \(u,v\) 的最近公共祖先 \(LCA(u,v)\)，我们可以先使 \(u,v\) 跳至同一高度（令 \(d[u]>d[v]\)），这时，我们便可以使用倍增算法 \(\mathcal O(\log n)\) 代替朴素 \(\mathcal O(n)\) 向上跳。

类似于二进制，从 \(2^{\log_2n+1}\) 到 \(2^0\) 依次尝试，如果从 \(u\) 跳至 \(f[u][i]\) 满足 \(d[f[u][i]] \geq d[v]\)，那就可以从 \(u\) 跳至 \(f[u][i]\)。

跳至同一高度后，再次倍增跳至相等的下一层，则 \(LCA(u,v)=f[u][0]=f[v][0]\)。（因为如果直接跳至 \(u=v\)，可能不是最近公共祖先）。

但是这样存在的问题就是，当 \(v\) 为 \(u\) 的祖先时，第一次跳完后便有 \(u=v\)，第二次倍增虽然不会跳，但是返回的 \(f[u][0]\) 是错误答案。因此，在第一次倍增跳完后加上特判：if(u==v)return u;。

查询代码如下：

int lca(int u,int v){
	if(d[u]<d[v])swap(u,v);
	for(int i=lg[d[u]-d[v]]-1;i>=0;i--){
		if(d[f[u][i]]>=d[v])u=f[u][i];
	}if(u==v)return u;
	for(int i=lg[d[u]]-1;i>=0;i--){
		if(f[u][i]!=f[v][i]){
			u=f[u][i];v=f[v][i];
		}
	}return f[u][0];
}

时间复杂度：\(\mathcal O(\log n)\)。

欧拉序+ST表

欧拉序是什么

DFS序的一种，但是DFS序只会在第一次访问的时候记录，而欧拉序无论访问还是回溯都需要记录。

比如这棵树的欧拉序：~~绝对不是我懒得画图~~

014

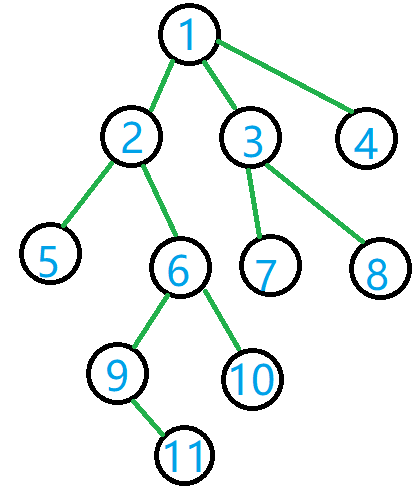
欧拉序为 \(1,2,5,2,6,9,11,9,6,10,6,2,1,3,7,3,8,3,1,4\)。

对于一棵节点数为 \(n\) 的树，其欧拉序长度为 \(2n-1\)。因为共有 \(n-1\) 条边，每条边访问两次会往欧拉序中加入两个节点，共计 \(2n-2\) 个节点，再加上根节点，共计 \(2n-1\) 个。

原理

令 \(f_x\) 表示节点 \(x\) 在欧拉序中第一次出现的位置。

那么：

\[LCA(u,v)=\Large \min_{i=f_u}^{f_v}d_{o_i} \]

其中，\(d_{o_i}\) 表示欧拉序中第 \(i\) 项的深度，且 \(f_u<f_v\)（不然直接交换 \(u,v\) 即可）。

那么这成为了一个RMQ问题，使用ST表求解即可。

关于其正确性，参考下图：

015

访问至 \(u\) 后，会回溯至 \(LCA(u,v)\)，随即访问 \(v\) 所在子树并最终访问至 \(v\)。

实现

预处理

先DFS一遍维护基本信息，包括：

点 \(x\) 的深度 \(d_x\)；
欧拉序第 \(i\) 项为 \(o_i\)；
点 \(x\) 在欧拉序中第一次出现的位置 \(f_x\)。

然后对 \(o\) 进行ST表求最小值的预处理即可。

代码如下：

const int N=500000,M=500000,N2=2*N; 
struct edge{
	int v,r;
}a[2*M+1];
int n,m,s,top,h[N+1],d[N+1],lg[N2+1],o[N2+1],st[N2+1][(int)log2(N2+1)+1],rest[N2+1][(int)log2(N2+1)+1],f[N+1];
void create(int u,int v){//链式前向星
	static int top=0;
	a[++top]={v,h[u]};
	h[u]=top;
}
void dfs(int p,int q){
	d[p]=d[q]+1;//深度
	o[++top]=p;//欧拉序
	if(f[p]==0)f[p]=top;//第一次出现的位置
	for(int i=h[p];i>0;i=a[i].r){
		if(a[i].v!=q){
			dfs(a[i].v,p);
			o[++top]=p;
		}
	}
}
void st_pre(){
	int n2=2*n-1;
	for(int i=0;i<=n2;i++)lg[i]=lg[i/2]+1;//常数优化
	for(int i=1;i<=top;i++){
		st[i][0]=d[o[i]];
		rest[i][0]=o[i]; 
	}
	for(int i=1;i<=lg[n2];i++){
		for(int x=1;x+(1<<i)-1<=n2;x++){
			st[x][i]=min(st[x][i-1],st[x+(1<<i-1)][i-1]);
			rest[x][i]=(st[x][i]==st[x][i-1]?rest[x][i-1]:rest[x+(1<<i-1)][i-1]);
		}
	}
}
void lca_pre(){
	dfs(s,0);
	st_pre();
}

时间复杂度：\(\mathcal O(n\log n)\)。

注意事项

需要注意的是，维护ST表求区间最小值时，还需要维护一个数组记录 \(st[x][i]\) 所对应的点 \(rest[x][i]\)。
ST表需要维护至欧拉序的长度 \(2n-1\)，而不是 \(n\)。

查询

这真的就没什么好说了，上代码：

int lca(int u,int v){
	if(f[u]>f[v])swap(u,v);
	int s=log2(f[v]-f[u]+1);
	return (st[f[u]][s]<st[f[v]-(1<<s)+1][s]?rest[f[u]][s]:rest[f[v]-(1<<s)+1][s]);
}

时间复杂度：\(\mathcal O(1)\)。

DFS序+ST表

其实，实质上也可以说成压缩欧拉序。

我们可以发现，“欧拉序+ST表”的解决方案预处理时，尽管时间复杂度为 \(\mathcal O(n\log n)\)，但常数较大。

因为欧拉序长度为 \(2n-1\)。

那么我们考虑在此基础上进行优化，可以发现欧拉序中会有重复的点，尝试去除这些点，由此，便有了此方案。

同时，由于这是上一个方案的优化版本，并不会进行详细解释。

同样对于这棵树：

014

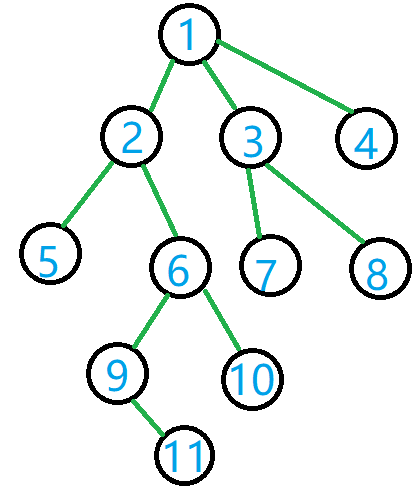
其DFS序为：\(1,2,5,6,9,11,10,3,7,8,4\)，长度为 \(n\)。

设 \(f_x\) 为节点 \(x\) 在DFS序中的位置。

对于节点 \(u,v\)，不妨令 \(f_u<f_v\)（不然交换）。

考虑到 \(u=v\) 时，直接返回 \(u\) 作为答案，因此 \(f_u<f_v\) 且 \(u\ne v\)。

\(u\) 不为 \(v\) 祖先时

考虑DFS遍历时是先从 \(LCA(u,v)\) 向下遍历至 \(u\)，随后回溯至 \(LCA(u,v)\) 的包含 \(v\) 的子树树根或其他子节点，再下行至 \(v\)。

那么在区间 \([f_u,f_v]\) 中任意深度最小的点的父节点即 \(LCA(u,v)\)。
\(u\) 为 \(v\) 的祖先时

显然，\(LCA(u,v)=u\)，且此时 \(u\) 至 \(v\) 为一条下行链。

考虑到此时再在区间 \([f_u,f_v]\) 中查找深度最小节点，必定查找到点 \(u\)，使最终答案不正确。

那么在区间 \([f_u+1,f_v]\) 中查找即可，因为这样必定查找到 \(f_u+1\) 对应点，其父节点即 \(u\)。

1.中同样可以查询 \([f_u+1,f_v]\)，因为 \(u\) 不为 \(v\) 祖先时，\(LCA(u,v)\) 不为 \(u\)，去除并不影响答案。

事实上，也可以查询区间 \([f_u+1,f_v-1]\)，然而在ST表 \(\mathcal O(1)\) 查询下，这不重要。

查询代码如下：

int lca(int u,int v){
	if(u==v)return u;
	if(f[u]>f[v])swap(u,v);
	int s=log2(f[v]-(f[u]+1)+1);
	return father[(st[f[u]+1][s] < st[f[v]-(1<<s)+1][s] ? rest[f[u]+1][s] : rest[f[v]-(1<<s)+1][s])];
}

仅仅是多了一个 \(father\) 数组表示父节点。

同时，原本需要开至 \(2n-1\) 大小的 \(lg,st,rest\) 等数组可以只需要开 \(n\) 个。

查询时间复杂度：\(\mathcal O(1)\)。

Tarjan 离线算法（DFS+并查集）

思想

问题存储

先一次性读入所有的询问（所有的 \(u_i,v_i\)）。随后以类似邻接表的方式存储，“建无向边”。

比如，输入：

那么建出来的“邻接表”便长这样：（事实上，这样做仅仅是为了能够快速找到有关节点，而又不浪费空间，与邻接表本身在图上的思想无关，请避免误会）

019

DFS+并查集

记：

节点 \(x\) 在图中的父节点为 \(father_x\)；
节点 \(x\) 在并查集中的父节点为 \(f_x\)；

当节点 \(x\) 需要回溯至 \(father_x\) 时，尝试计算LCA的答案并将 \(x\) 和 \(father_x\) 并入一个集合。即：\(f_x=father_x\)。

假设当前访问节点 \(x=v_i\)，那么如果 \(u_i\) 已经访问过，则 \(LCA(u_i,v_i)=find(u_i)=find(v_i)\)，其中 \(find(x)\) 表示 \(x\) 所在集合的根。

关于正确性：同样地，参考此图。
015
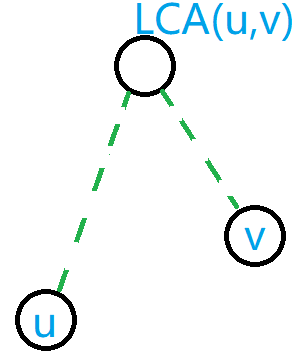
此时 \(u_i,v_i\) 都属于包含 \(LCA(u_i,v_i)\) 的集合，则 \(find(u_i)=find(v,i)=LCA(u_i,v_i)\)。

最后，当DFS结束时，所有答案便离线得出了。

预处理

首先初始化一个并查集，即对于整数 \(i\in[1,n]\)，使得\(f_i=i\)。

随后使用类“邻接表”存储询问 \(u_i,v_i\)。

再调用 tarjan()：

void tarjan(int x){
    //三种状态：0-没有访问到,1-访问到了没有回溯,2-已经回溯
	static int vis[N+1];
	vis[x]=1;
	for(int i=h[x];i>0;i=a[i].r){
		if(vis[a[i].v])continue;//其实就是访问到了父节点,跳过
		tarjan(a[i].v);
		f[a[i].v]=x;//并查集合并
	}for(int i=hq[x];i>0;i=q[i].r){
		if(q[i].v)ans[q[i].id]=find(q[i].v);//通过id找到对应问题记录答案
	}vis[x]=2;
}

最后一个简单的输出：

for(int i=1;i<=m;i++)printf("%d\n",ans[i]);

树链剖分 LCA

树链剖分 LCA 在不考虑树链剖分代码长度下，甚至可以说是最简单的。

然而考虑到树链剖分代码冗长，且树链剖分 LCA 完完全全以树链剖分为基础，本文不再赘述。

参见此处。

各种LCA算法的比较

倍增算法

预处理时间复杂度：\(\mathcal O(n\log n)\)。

查询时间复杂度：\(\mathcal O(\log n)\)。

空间复杂度：\(\mathcal O(n\log n)\)。

欧拉序+ST表

预处理时间复杂度：\(\mathcal O(2n\log 2n)\)。

查询时间复杂度：\(\mathcal O(1)\)。

空间复杂度：\(\mathcal O(2n\log 2n)\)。

注：使用 \(2n\) 是为了与”DFS序+ST表“形成对比。

DFS序+ST表

预处理时间复杂度：\(\mathcal O(n\log n)\)。

查询时间复杂度：\(\mathcal O(1)\)。

空间复杂度：\(\mathcal O(n\log n)\)。

Tarjan 离线算法

预处理时间复杂度：\(\mathcal O(n)\)。

求解时间复杂度：\(\mathcal O(m\alpha(m+n,n)+n)\)。

空间复杂度：\(\mathcal O(n+m)\)。

并不存在「朴素 Tarjan LCA 算法中使用的并查集性质比较特殊，单次调用 find() 函数的时间复杂度为均摊 \(\mathcal O(1)\)」这种说法。

以下的朴素 Tarjan 实现复杂度为 \(\mathcal O(m\alpha(m+n,n)+n)\)。如果需要追求严格线性，可以参考 Gabow 和 Tarjan 于 1983 年的论文。其中给出了一种复杂度为 \(\mathcal O(n+m)\) 的做法。——OI Wiki

树链剖分 LCA

预处理时间复杂度：\(\mathcal O(n)\)。

查询时间复杂度：\(\mathcal O(\log n)\)。

空间复杂度：\(\mathcal O(n)\)。

汇总

倍增相对而言更加好理解，更加适合初学者，但复杂度较劣。

DFS序+ST表的复杂度较优，代码也并不难理解，适合使用。

欧拉序+ST表不如DFS序+ST表。

Tarjan 离线算法虽然复杂度最优，但常数较大，且可能并不是那么的好理解。

树链剖分除非是题目已经使用了树链剖分，否则不建议使用。

练习题（参考代码）

【模板】最近公共祖先（LCA）

倍增算法

参考代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=500000;
//邻接表:链式前向星 
struct edge{
	int v,r;
}a[2*N+1];
//d[i]:节点i的深度(第几层),f[i][j]:节点i的2^j级祖先(向上寻找2^j次父节点) 
int n,m,s,x,y,h[N+1],d[N+1],f[N+1][32],lg[N+1];
//创建一条边(u,v) 
void create(int u,int v){
	static int top=0;
	a[++top]={v,h[u]};
	h[u]=top;
}
//q:p的父节点 
void dfs(int p,int q){
	//基本信息 
	f[p][0]=q;//2^0=1,即p的父节点,q 
	d[p]=d[q]+1;//下一层 
	for(int i=h[p];i>0;i=a[i].r){
		if(a[i].v!=q)dfs(a[i].v,p);
	}
}
void lca_pre(){
	dfs(s,0);
	for(int i=1;i<=n;i++)lg[i]=lg[i/2]+1;
	for(int i=1;i<=lg[n];i++){
		for(int x=1;x<=n;x++)f[x][i]=f[f[x][i-1]][i-1];
	}
}
int lca(int u,int v){
	if(d[u]<d[v])swap(u,v);
	for(int i=lg[d[u]-d[v]]-1;i>=0;i--){
		if(d[f[u][i]]>=d[v])u=f[u][i];
	}if(u==v)return u;
	for(int i=lg[d[u]]-1;i>=0;i--){
		if(f[u][i]!=f[v][i]){
			u=f[u][i];v=f[v][i];
		}
	}return f[u][0];
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/

	scanf("%d %d %d",&n,&m,&s);
	for(int i=1;i<n;i++){
		scanf("%d %d",&x,&y);
		create(x,y);create(y,x);
	}lca_pre(); 
	while(m--){
		scanf("%d %d",&x,&y);
		printf("%d\n",lca(x,y));
	}
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

欧拉序+ST表

参考代码

//#include<bits/stdc++.h>
#include<algorithm> 
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=500000,M=500000,N2=2*N; 
struct edge{
	int v,r;
}a[2*M+1];
int n,m,s,top,h[N+1],d[N+1],lg[N2+1],o[N2+1],st[N2+1][(int)log2(N2+1)+1],rest[N2+1][(int)log2(N2+1)+1],f[N+1];
void create(int u,int v){
	static int top=0;
	a[++top]={v,h[u]};
	h[u]=top;
}
void dfs(int p,int q){
	d[p]=d[q]+1;
	o[++top]=p;
	if(f[p]==0)f[p]=top;
	for(int i=h[p];i>0;i=a[i].r){
		if(a[i].v!=q){
			dfs(a[i].v,p);
			o[++top]=p;
		}
	}
}
void st_pre(){
	int n2=2*n-1;
	for(int i=0;i<=n2;i++)lg[i]=lg[i/2]+1;
	for(int i=1;i<=top;i++){
		st[i][0]=d[o[i]];
		rest[i][0]=o[i]; 
	}
	for(int i=1;i<=lg[n2];i++){
		for(int x=1;x+(1<<i)-1<=n2;x++){
			st[x][i]=min(st[x][i-1],st[x+(1<<i-1)][i-1]);
			rest[x][i]=(st[x][i]==st[x][i-1]?rest[x][i-1]:rest[x+(1<<i-1)][i-1]);
		}
	}
}
void lca_pre(){
	dfs(s,0);
	st_pre();
}
int lca(int u,int v){
	if(f[u]>f[v])swap(u,v);
	int s=log2(f[v]-f[u]+1);
	return (st[f[u]][s]<st[f[v]-(1<<s)+1][s]?rest[f[u]][s]:rest[f[v]-(1<<s)+1][s]);
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/

	scanf("%d %d %d",&n,&m,&s);
	for(int i=1;i<n;i++){
		int x,y;
		scanf("%d %d",&x,&y);
		create(x,y);create(y,x);
	}lca_pre(); 
	while(m--){
		int x,y;
		scanf("%d %d",&x,&y);
		printf("%d\n",lca(x,y));
	}
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

DFS序+ST表

参考代码

//#include<bits/stdc++.h>
#include<algorithm> 
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=500000,M=500000; 
struct edge{
	int v,r;
}a[2*M+1];
int n,m,s,top,h[N+1],d[N+1],lg[N+1],o[N+1],st[N+1][(int)log2(N+1)+1],rest[N+1][(int)log2(N+1)+1],f[N+1],father[N+1];
void create(int u,int v){
	static int top=0;
	a[++top]={v,h[u]};
	h[u]=top;
}
void dfs(int p,int q){
	father[p]=q;
	d[p]=d[q]+1;
	o[++top]=p;
	if(f[p]==0)f[p]=top;
	for(int i=h[p];i>0;i=a[i].r){
		if(a[i].v!=father[p])dfs(a[i].v,p);
	}
}
void st_pre(){
	for(int i=0;i<=n;i++)lg[i]=lg[i/2]+1;
	for(int i=1;i<=top;i++){
		st[i][0]=d[o[i]];
		rest[i][0]=o[i]; 
	}
	for(int i=1;i<=lg[n];i++){
		for(int x=1;x+(1<<i)-1<=n;x++){
			st[x][i]=min(st[x][i-1],st[x+(1<<i-1)][i-1]);
			rest[x][i]=(st[x][i]==st[x][i-1]?rest[x][i-1]:rest[x+(1<<i-1)][i-1]);
		}
	}
}
void lca_pre(){
	dfs(s,0);
	st_pre();
}
int lca(int u,int v){
	if(u==v)return u;
	if(f[u]>f[v])swap(u,v);
	int s=log2(f[v]-(f[u]+1)+1);
	return father[(st[f[u]+1][s] < st[f[v]-(1<<s)+1][s] ? rest[f[u]+1][s] : rest[f[v]-(1<<s)+1][s])];
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/

	scanf("%d %d %d",&n,&m,&s);
	for(int i=1;i<n;i++){
		int x,y;
		scanf("%d %d",&x,&y);
		create(x,y);create(y,x);
	}lca_pre(); 
	while(m--){
		int x,y;
		scanf("%d %d",&x,&y);
		printf("%d\n",lca(x,y));
	}
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

Tarjan 离线算法（DFS+并查集）

参考代码

//#include<bits/stdc++.h>
#include<algorithm> 
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=5e5,M=5e5;
//邻接表
struct edge{
	int v,r;
}a[2*N+1];
struct problem{
	int v,r,id;
}q[2*M+1];
int n,m,s,h[N+1],hq[N+1],f[N],ans[N];
void create(int u, int v) {
	static int top;
	a[++top]={v,h[u]};
	h[u]=top;
}
void create2(int u,int v,int id){
	static int top;
	q[++top]={v,hq[u],id};
	hq[u]=top;
}
int find(int x){//路径压缩
	if(f[x]!=x)return f[x]=find(f[x]);
	return x;
}
void tarjan(int x){
	static int vis[N+1];
	vis[x]=1;
	for(int i=h[x];i>0;i=a[i].r){
		if(vis[a[i].v])continue;
		tarjan(a[i].v);
		f[a[i].v]=x;//加入并查集
	}for(int i=hq[x];i>0;i=q[i].r){
		if(vis[q[i].v]==2)ans[q[i].id]=find(q[i].v);//记录答案
	}vis[x]=2;//已经回溯过
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/

	scanf("%d %d %d",&n,&m,&s);
	for(int i=1;i<=n;i++)f[i]=i;
	for(int i=1;i<n;i++){
		int u,v;
		scanf("%d %d",&u,&v);
		create(u,v);create(v,u);
	}for(int i=1;i<=m;i++){
		int x,y;
		scanf("%d %d",&x,&y);
		if(x==y)ans[i]=x;
		else create2(x,y,i),create2(y,x,i);
	}tarjan(s);
	for(int i=1;i<=m;i++)printf("%d\n",ans[i]);
	
	/*fclose(stdin); 
	fclose(stdout);*/
	return 0;
}

树链剖分 LCA

参见此处。

[NOIP2013 提高组] 货车运输

思路分析

让每一辆车的载重限制都尽可能大，在图上建最大生成树，然后树上求LCA即可。（本处仅给出倍增算法的参考代码）

参考代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=1e4,M=5e4;
struct edge{
	int u,v,w;
}x[M+1];
struct edge_tree{
	int v,r,w;
}a[2*M+1];
int n,m,u,v,w,q,f[N+1],h[N+1],lg[N+1],d[N+1],pl[N+1][31],dis[N+1][31];
bool vis[N+1];
void create(int u,int v,int w){
	static int top=0;
	a[++top]={v,h[u],w};
	h[u]=top;
}
int find(int x){
	if(f[x]!=x)return f[x]=find(f[x]);
	return x;
}
void unite(int x,int y){
	f[find(x)]=find(y);
}
bool cmp(edge a,edge b){
	return a.w>b.w;
}
void Kruskal(){
	sort(x+1,x+m+1,cmp);
	for(int i=1;i<=n;i++)f[i]=i;
	for(int i=1,cnt=0;i<=m&&cnt<n-1;i++){
		if(find(x[i].u)!=find(x[i].v)){
			unite(x[i].u,x[i].v);
			create(x[i].u,x[i].v,x[i].w);
			create(x[i].v,x[i].u,x[i].w);
		}
	}
}
void dfs(int p,int q,int w){
	vis[p]=true;
	pl[p][0]=q;
	dis[p][0]=w;
	d[p]=d[q]+1;
	for(int i=1;i<=lg[d[p]];i++){
		pl[p][i]=pl[pl[p][i-1]][i-1];
		dis[p][i]=min(dis[p][i-1],dis[pl[p][i-1]][i-1]);
	}for(int i=h[p];i>0;i=a[i].r){
		if(a[i].v!=q)dfs(a[i].v,p,a[i].w);
	}
}
int lca(int u,int v){
	if(find(u)!=find(v))return -1;
	int ans=2147483647;
	if(d[u]<d[v])swap(u,v);
	while(d[u]>d[v]){
		ans=min(ans,dis[u][lg[d[u]-d[v]]-1]);
		u=pl[u][lg[d[u]-d[v]]-1];
	}if(u==v)return ans;
	for(int i=lg[d[u]]-1;i>=0;i--){
		if(pl[u][i]!=pl[v][i]){
			ans=min(ans,min(dis[u][i],dis[v][i]));
			u=pl[u][i];
			v=pl[v][i];
		}
	}ans=min(ans,min(dis[u][0],dis[v][0]));
	return ans;
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/

	scanf("%d %d",&n,&m);
	for(int i=1;i<=m;i++)scanf("%d %d %d",&x[i].u,&x[i].v,&x[i].w);
	Kruskal();
	for(int i=1;i<=n;i++)lg[i]=lg[i/2]+1;
	for(int i=1;i<=n;i++){
		if(vis[i]==false)dfs(i,0,0);
	}
	scanf("%d",&q);
	while(q--){
		scanf("%d %d",&u,&v);
		printf("%d\n",lca(u,v));
	}
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

posted @ 2025-07-19 22:45 TH911 阅读(10) 评论(0) 收藏举报

刷新页面返回顶部

TH911 Blog

光阴不可测，岁月亦无歌。

树上最近公共祖先（LCA）问题

倍增LCA

倍增思想

预处理

查询

欧拉序+ST表

欧拉序是什么

原理

实现

预处理

注意事项

查询

DFS序+ST表

Tarjan 离线算法（DFS+并查集）

思想

问题存储

DFS+并查集

预处理

树链剖分 LCA

各种LCA算法的比较

倍增算法

欧拉序+ST表

DFS序+ST表

Tarjan 离线算法

树链剖分 LCA

汇总

练习题（参考代码）

【模板】最近公共祖先（LCA）

倍增算法

欧拉序+ST表

DFS序+ST表

Tarjan 离线算法（DFS+并查集）

树链剖分 LCA

[NOIP2013 提高组] 货车运输

思路分析

公告