题解：[POI2008] BLO-Blockade

题目传送门

前置知识：Tarjan 求割点

不会可以看看。

题意分析

给定 \(n\) 个点，\(m\) 条边的无向图，点从 \(1\) 至 \(n\) 标号。

求对于每一个点 \(i\)，删除该点后不连通的有序点对 \((x,y)\) 的个数。

保证给定图连通。

割点

因为原图连通，所以最开始时对于任意两个点都是连通的。

而删去某个点 \(i\) 后如果存在点对 \((x,y)\) 满足点 \(x\) 和点 \(y\) 不连通，显然点 \(i\) 是一个割点。

不为割点时的答案

当点 \(i\) 不为割点时，那么答案就是其他点和点 \(i\) 不连通形成的点对，即 \(2(n-1)\)。

为割点时的答案

以求样例中点 \(4\) 的答案为例。

首先点 \(4\) 的答案 \(14\) 对应的是以下几组（和反过来的）：

编号	\(x\)	\(y\)
\(1\)	\(1\)	\(4\)
\(2\)	\(1\)	\(5\)
\(3\)	\(2\)	\(4\)
\(4\)	\(2\)	\(5\)
\(5\)	\(3\)	\(4\)
\(6\)	\(3\)	\(5\)
\(7\)	\(4\)	\(5\)

画一下样例的 DFS 生成树：

显然，点 \(3,4\) 是割点。

删除点 \(4\) 后，原图会断成两个连通块：\((1,3,4)\) 和 \((5)\)。

如图：

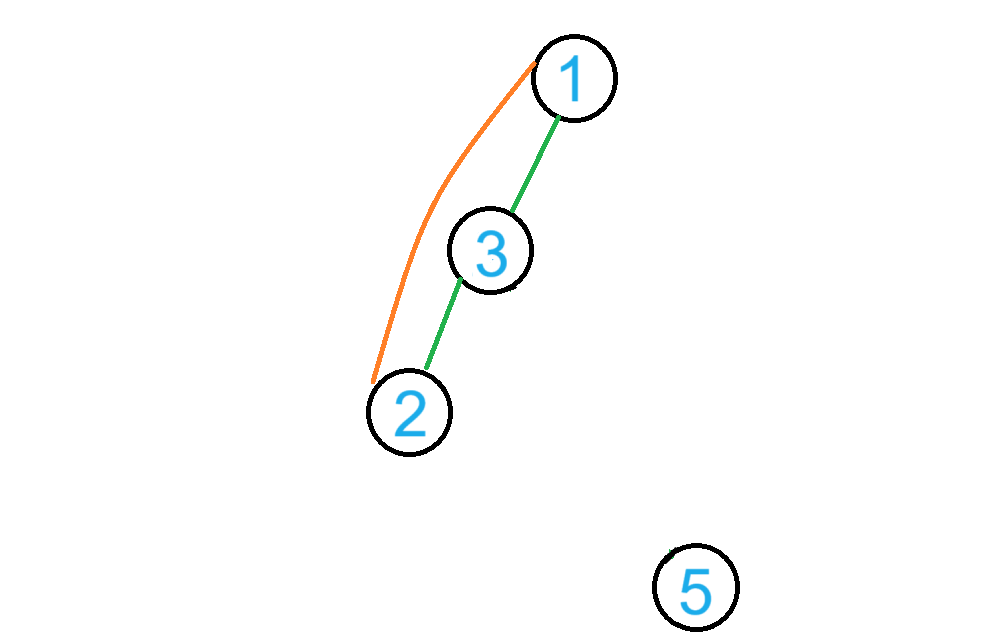
用各个连通块乘起来即可。

具体而言，就是令连通块的个数分别为 \(y_1,y_2,y_3,\cdots,y_k\)，则答案为：

\[\sum_{i=1}^k y_i\times(n-y_i) \]

解释：连通块中的每一个点都不能到达连通块外的点，\(n\) 为总点数。

因为 Tarjan 算法的本质就是个 DFS，我们可以在 Tarjan 的过程中来计算。

对于在 DFS 生成树上不是父节点的能够到达的节点，可以使用 \(n-\sum\limits_{i=1}^ky_i-1\) 来求出该连通块大小。

但是需要注意的是，由于回溯边在 DFS 生成树上的存在，直接算答案可能会出问题。

以求点 \(3\) 的答案为例，直接求会重复计算 \(1,2\) 的答案，然而实际上 \(1,2\) 是一个连通块。

解决方法就是令 \(size_x\) 表示在 DFS 生成树上点 \(x\) 的子树大小，\(sonSize\) 表示当前点 \(x\) 的不重复统计的子树大小。具体而言就是对于子节点 \(v\)，当且仅当 \(low_v\geq dfn_x\) 时，才会将 \(size_v\) 计入 \(sonSize\) 内。

这样，就有效避免了重复计数。

注：\(n-sonSize-1\) 表示的就是节点 \(x\) 及其子树的大小。

AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
#define int long long 
using namespace std;
const int N=100000,M=500000;
struct graph{
	struct edge{
		int v,r;
	}a[2*M+1];
	
	int h[N+1];
	void create(int u,int v){
		static int top;
		a[++top]={v,h[u]};
		h[u]=top;
	}
}g;
int n,m,ans[N+1];
void Tarjan(int x,int fx,int root){
	static int cnt,dfn[N+1],low[N+1],size[N+1];
	dfn[x]=low[x]=++cnt;
	size[x]=1;
	int son=0,pl=n-1,sonSize=0;
	for(int i=g.h[x];i;i=g.a[i].r){
		int &v=g.a[i].v;
		if(!dfn[v]){
			Tarjan(v,x,root);
			low[x]=min(low[x],low[v]);
			size[x]+=size[v];
			if(low[v]>=dfn[x]){
				son++;
				sonSize+=size[v];
				if(v!=fx){
					pl+=(n-size[v])*size[v];
				}
			}
		}else{
			low[x]=min(low[x],dfn[v]);
		}
	}sonSize++;
	pl+=(n-sonSize)*sonSize;
	bool cut=false;
	if(x==root){
		if(son>1)cut=true;
	}else{
		if(son>0)cut=true;
	}
	if(!cut)ans[x]=(n-1)<<1;
	else ans[x]=pl;
}
main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	scanf("%lld %lld",&n,&m);
	while(m--){
		int u,v;
		scanf("%lld %lld",&u,&v);
		g.create(u,v);
		g.create(v,u);
	}Tarjan(1,0,1);
	for(int i=1;i<=n;i++)printf("%lld\n",ans[i]);
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}