题解：[USACO12DEC] First! G

题目传送门

如果你还不会 Trie树：看这里

题意分析

策略

看到字典序，很容易想到考虑使用 Trie 树解决。

假设 \(s\) 为更改字典序后可能的最小值，那么相当于钦定了 \(s_i\) 小于其兄弟节点。（如图）

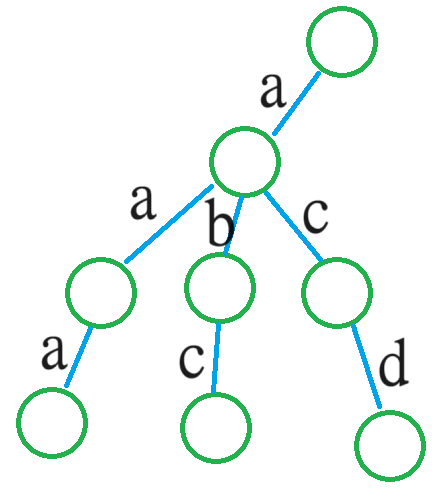
假设 \(s=\texttt{acd}\)，那么就钦定了 \(c<a,c<b\)，否则最小值不可能为 \(\texttt{acd}\)。

至此，思路就比较明确了：遍历字典树，如果走到了模式串末端节点（依据权值判断）那么就记录答案，否则继续走。

走的时候需要判断是否符合我们钦定的规则，即不能同时出现类似于 \(a<b\land a>b\) 的情况。

（不会有人不知道 \(\land\) 是什么意思吧......“且”）

那么我们只需要再遍历时记录下我们钦定的规则，至于这个怎么存，建立一个有向图即可。

如果 \(u<v\)，那么就建一条有向边从 \(u\) 指向 \(v\)，判断是否存在规则的时候判断联通即可。

注意：不可直接判断边，需要跑图。

因为可能存在于类似 \(a<b\land b<c\)​ 的情况，此时 \(a<c\) 依然成立，但 \(a,c\) 之间没有边。

然后判断能否钦定 \(u<v\)，就先在建的图上判断 \(u,v\) 是否联通，联通则代表不能钦定。

最后按照顺序输出即可。

为什么可以使用图

这其实就涉及到图的本质了。 图本质就是多对多元素间的关系，所以不要被局限了。

输出

其实这个输出实现的方法有很多，这里给出一种牺牲一点时间但是好理解的：

1. 按照字典序排序
2. 去重
3. 按照输入顺序排序
4. 顺序输出

代码也很简单：

sort(ans.begin(),ans.end());
ans.resize(unique(ans.begin(),ans.end())-ans.begin());
sort(ans.begin(),ans.end(),cmp);
cout<<ans.size()<<endl;
for(int i=0;i<ans.size();i++)cout<<ans[i]<<endl;

当然，如果你想追求极致的时间，可以考虑双关键字排序或者存储答案的出现次序然后排序、去重、输出。

时间复杂度

没什么好说的：\(\mathcal O\left(n\log n\right)\)。

AC代码

//#include<bits/stdc++.h>
#include<algorithm> 
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
#include<unordered_map>
using namespace std;
const int N=30000,X=300000;
unordered_map<string,int>order;
int top,e[26][26];
vector<string>ans;
struct node{
	int m[26];//值域不大,直接开数组即可,无需map/unordered_map
	bool flag;
}a[X+1];
void insert(string &s){
	int p=0;
    for(int i=0;i<s.size();i++){
        if(a[p].m[s[i]-'a']==0)a[p].m[s[i]-'a']=++top;
        p=a[p].m[s[i]-'a'];
    }a[p].flag=true;
}
bool cmp(string &a,string &b){
	return order[a]<order[b];//牺牲点常数,节约点脑子
}//判断联通
bool check(int u,int v){
	if(u==v)return true;
	for(int i=0;i<26;i++){
		if(e[u][i]&&check(i,v))return true;
	}return false;
}
void dfs(int p,string step){
	if(a[p].flag){
		ans.push_back(step);
		return;
	}
	for(int i=0;i<26;i++){
		if(!a[p].m[i])continue;
		bool flag=true;
		for(int j=0;j<26;j++){
			if(i==j||!a[p].m[j])continue;
			if(check(j,i)){
				flag=false;
				break;
			}
		}if(!flag)continue;
		for(int j=0;j<26;j++){
			if(i==j||!a[p].m[j])continue;
			e[i][j]++;
		}
		dfs(a[p].m[i],step+(char)(i+'a'));
		for(int j=0;j<26;j++){
			if(i==j||!a[p].m[j])continue;
			e[i][j]--;
		}
	}
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	int n;
	scanf("%d",&n);
	string s;
	for(int i=1;i<=n;i++){
		cin>>s;
		order[s]=i;
		insert(s);
	}dfs(0,"");
	sort(ans.begin(),ans.end());
	ans.resize(unique(ans.begin(),ans.end())-ans.begin());
	sort(ans.begin(),ans.end(),cmp);
	cout<<ans.size()<<endl;
	for(int i=0;i<ans.size();i++)cout<<ans[i]<<endl;
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}