题解：字典树

题目传送门

字典树（Trie树）

字典树其实就是一种空间换时间的策略。

比如我们使用 \(\texttt{aa,ab,ac,abc,acd,aac}\) 来构造一棵字典树，则如下图：

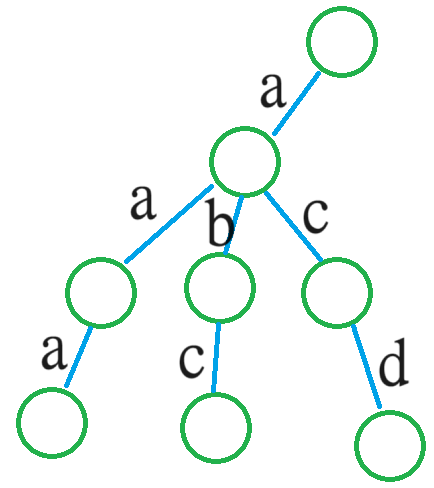
简单而言，就是将每一位字符都视作连接节点的两条边，那么便形成了如上的树。

这么做有什么好处呢？

节约时间。

这样查询前缀，仅仅需要在字典树上找到 \(t\) 的最后一个字符，然后统计字数权值和即可。

每一个节点如果其是某个模式串的最后一个节点，那么其权值为 \(1\)，否则为 \(0\)。

代码实现

更新：$2025/1/19$

请不要使用 unordered_map，极其容易导致 $\text{MLE}$。

首先，存储每一个节点：

struct node{
	unordered_map<char,int>m;
	int value;
}a[X+1];

这里使用了 unordered_map，但你当然也可以手写离散化字符然后在里面开数组存储。

然后是插入函数：

void insert(char s[]){
	int p=0,len=strlen(s);
    for(int i=0;i<len;i++){
        if(a[p].m[s[i]]==0)a[p].m[s[i]]=++top;
        p=a[p].m[s[i]];
    }a[p].value++;
}

如果有则直接走，没有就创建子节点。

最后将 \(p.value\) 增加 \(1\)，含义同上权值。

查询函数：

int query(char t[]){
	int p=0,len=strlen(t);
	for(int i=0;i<len;i++){
		if(a[p].m[t[i]])p=a[p].m[t[i]];
		else return 0;
	}return a[p].value;
}

如果走着走着 \(t\) 没走完但是没有路走了，那就证明 \(t\) 不是任何一个 \(s_i\) 的前缀，返回 \(0\)。

---

但是，到这里就会发现一个问题：\(value\) 没有计算。

所以再写一个预处理：

void dfs(int p){
	for(auto i:a[p].m){
		dfs(i.second);
		a[p].value+=a[i.second].value;
	}
}

应当注意的是，不应该每一次都进行搜索，就算不预处理，也应该使用记忆化。

AC代码

//#include<bits/stdc++.h>
#include<algorithm> 
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
#include<unordered_map>
using namespace std;
const int N=1e5,X=3e6;
char s[X+1],t[X+1];
int top;
struct node{
	unordered_map<char,int>m;
	int value;
}a[X+1];
void dfs(int p){
	for(auto i:a[p].m){
		dfs(i.second);
		a[p].value+=a[i.second].value;
	}
}
void insert(char s[]){
	int p=0,len=strlen(s);
    for(int i=0;i<len;i++){
        if(a[p].m[s[i]]==0)a[p].m[s[i]]=++top;
        p=a[p].m[s[i]];
    }a[p].value++;
}
int query(char t[]){
	int p=0,len=strlen(t);
	for(int i=0;i<len;i++){
		if(a[p].m[t[i]])p=a[p].m[t[i]];
		else return 0;
	}return a[p].value;
}
void Start(){
	for(int i=0;i<=top;i++)a[i]={};
	top=0;
} 
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	int T;
	scanf("%d",&T);
	while(T--){
		Start();
		int n,q;
		scanf("%d %d",&n,&q);
		for(int i=1;i<=n;i++){
			scanf("%s",s);
			insert(s);
		}dfs(0);
		while(q--){
			scanf("%s",t);
			printf("%d\n",query(t));
		}
	} 
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

注意事项

多测清空

多测不清空，光速见祖宗。

清空的时候，要么 fill()，不然就 memset() 部分。如果直接使用 memset(a,0,sizeof(a))，会 \(\text{TLE}\)。

空间大小

\(26\) 倍。

字典序的空间复杂度是 \(\mathcal O(VL)\) 的，\(V\) 表示字符集大小，\(L\) 表示总输入字符串长度。