题解：[NOI2005] 维护数列

考虑到P2710 数列和P2042 [NOI2005]维护数列的区别仅仅是一个可以被转换为其他操作的操作和数组大小，放到一篇。

题意分析

需要维护的操作有：

区间插入
区间删除
区间翻转
区间覆盖
区间求和
单点查询
求区间最大子段和

我们可以通过平衡树 FHQ Treap 来维护区间信息。

FHQ Treap 维护区间信息见 FHQ Treap 之区间操作。

以下代码基于：

struct node{
    int left,right;
    int value,rand,size;
    //maxsum:最大子段和
    //pre/suf:子树区间的最大前缀/后缀和,可以为0
    int set,sum,maxsum,pre,suf;
    bool reverse;
    node(){
        set=114514;
    }
    void clear(){
        left=right=value=rand=size=set=sum=maxsum=pre=suf=0;
        reverse = false;
    }
}t[N+1];

区间插入、删除

FHQ Treap 分裂后操作即可。

注意 INSERT 操作时最好不要将整棵树分裂 \(n\) 次再合并 \(n\) 次，因为这样常数较大。

建议先将 \(n\) 个数建一棵树，然后再合并到整棵树上。

例如：

void insert(int x,int n){
    int pl;
    scanf("%d",&pl);
    int p=create(pl);
    for(int i=2;i<=n;i++){
        scanf("%d",&pl);
        p=merge(p,create(pl));
    }
    int l,r;
    split(root,x,l,r);
    root=merge(merge(l,p),r);
}

区间翻转

打标记 t[i].reverse 即可。

警告

更新 reverse 时，需要交换左右子节点和前后缀最大和（见下文）。

区间覆盖

打标记 t[i].set 传递即可。

注意：set 不能设为 \(0\)，请设置为值域 \([-10^3,10^3]\) 之外。

~~我设置的 114514~~。

区间求和

维护标记 t[i].sum。

求区间最大子段和

维护标记 t[i].maxsum。

标记下传与更新上传

更新上传：\(up()\)

首先明确需要更新的信息：size、sum、maxsum、pre 和 suf。

size 明显是左右子节点的 size 加 \(1\)。

sum 是左右子节点的 sum 加自己的权值。

如图，pre 分两种情况：

013

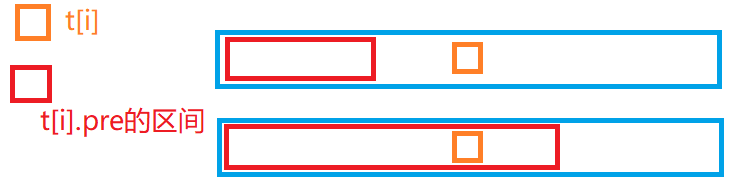
pre 有可能不过当前节点 t[p]，那么就是左子树区间的 pre，即 t[t[p].left].pre。或者经过 t[i]，那么就是整个左子树区间的和（sum）加上自己的权值（value）再加右子树区间的最大 pre。

可能会存在不选择右子树区间的 pre 的情况，因此我们令 pre 与 \(0\) 取 max即可。当 \(pre>0\) 的时候，明显选择会比不选更优。

即：

t[p].pre = max(t[t[p].left].pre,t[t[p].left].sum + t[p].value + t[t[p].right].pre,0);

同理：

t[p].suf = max(t[t[p].right].suf,t[t[p].left].suf + t[p].value + t[t[p].right].sum,0);

类似的，maxsum 要么不过当前节点：

max(t[t[p].left].maxsum,t[t[p].right].maxsum);

要么就是：

t[p].maxsum = t[t[p].left].suf + t[p].value + t[t[p].right].pre;

参考代码

void up(int p){
	/*
	int left,right;
	int value,rand,size;
	int set,sum,maxsum,pre,suf;
	*/
	
	t[0].clear();
	int &left = t[p].left;
	int &right = t[p].right;
	
	t[p].size = t[left].size + 1 + t[right].size;
	t[p].sum = t[left].sum + t[p].value + t[right].sum;
	t[p].pre = max(t[left].pre,t[left].sum + t[p].value + t[right].pre,0);
	t[p].suf = max(t[right].suf,t[left].suf + t[p].value + t[right].sum,0);
	t[p].maxsum = t[left].suf + t[p].value + t[right].pre;
	if(left){
		t[p].maxsum = max(t[p].maxsum,t[left].maxsum);
	} 
	if(right){
		t[p].maxsum = max(t[p].maxsum,t[right].maxsum);
	}
}

标记下传：\(down()\)

我们一共打了两个懒标记：set 和 reverse。

首先对于 reverse，很好理解，左右子节点的 reverse 分别取反后交换其左右子节点和 pre、suf 即可。

警告

请不要忘记交换 pre 和 suf，因为区间翻转了，前、后缀也会交换，因此最大和也应当交换。

对于 set，需要在下传之前判断子节点是否存在，不存在则不下传。

然后记得 pre、suf 可以取 \(0\)。

注意 set 要清空为一个值域之外的值。

void down(int p){
    t[0].clear();
    int &left = t[p].left;
    int &right = t[p].right;
    if(t[p].set != 114514){

        if(left){
            t[left].sum = t[left].size * t[p].set;
            t[left].maxsum = max(t[p].set,t[left].sum);
            t[left].pre = max(t[left].sum,0);
            t[left].suf = max(t[left].sum,0);
            t[left].value = t[p].set;
            t[left].set = t[p].set;
        }
        if(right){
            t[right].sum = t[right].size * t[p].set;
            t[right].maxsum = max(t[p].set,t[right].sum);
            t[right].pre = max(t[right].sum,0);
            t[right].suf = max(t[right].sum,0);
            t[right].value = t[p].set;
            t[right].set = t[p].set;
        }
        t[p].set=114514;
    }if(t[p].reverse){
        if(left){
            t[left].reverse = !t[left].reverse;
            swap(t[left].left,t[left].right);
            swap(t[left].pre,t[left].suf);
        } 
        if(right){
            t[right].reverse = !t[right].reverse;
            swap(t[right].left,t[right].right);
            swap(t[right].pre,t[right].suf);
        }
        t[p].reverse = false;
    }
    t[0].clear();
}

内存回收

需要回收，因为保证数列中的数的数量不超过 \(200000\)，而直接开最大为 \(N+M\times 1000=2(10^7+10^5)\)，会导致 \(\text{MLE}\)。

封装一个结构体：

struct mem{
    vector<int>q;
    mem(){
        q.resize(0);
    }
    int ask(){
        if(q.size()){
            int x=q.back();
            q.pop_back();
            return x;
        }else{
            static int top;
            return ++top;
        }
    }
    void remove(int p){
        q.push_back(p);
    }
}mem;

需要分配内存时，调用 mem.ask() 即可。

具体操作

~~没什么好说的~~。

注意事项

维护的 pre、suf 可以为 \(0\)，无论是创建节点、更新上传还是标记下传，都需要和 \(0\) 取 max。
维护的 maxsum 不能为 \(0\)，即连续子序列不能为空。
翻转区间时需要交换 pre、suf 值。
随时清空 \(0\) 号节点，不然就处处判断是否有子节点。

AC 代码

保留了调试的注释。~~让你们看看我调了 7h 的结果。~~

P2710 数列

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath> 
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
#include<random>
#define cerr cout
//#define int long long
using namespace std;
typedef long long ll;
mt19937 Rand(123456/*time(0)*/);
const int N=2e5;
int max(int a,int b){
	return (a>b?a:b);
}
int max(int a,int b,int c){
	return (a>b?(a>c?a:c):(b>c?b:c));
}
int root;
struct treap{
	struct node{
		int left,right;
		int value,rand,size;
		//pre/suf:node所在子树对应的区间的前/后缀最大和. 
		int set,sum,maxsum,pre,suf;
		bool reverse;
		node(){
			set=114514;
		}
		void clear(){
			left=right=value=rand=size=set=sum=maxsum=pre=suf=0;
			reverse = false;
		}
	}t[N+1];
	
	struct mem{
		vector<int>q;
		mem(){
			q.resize(0);
		}
		int ask(){
			if(q.size()){
				int x=q.back();
				q.pop_back();
				return x;
			}else{
				static int top;
				return ++top;
			}
		}
		void remove(int p){
			q.push_back(p);
		}
	}mem;
	
	void up(int p){
		/*
		int left,right;
		int value,rand,size;
		int set,sum,maxsum,pre,suf;
		*/
		
		t[0].clear();
//		//cerr<<"::"<<t[0].left<<endl;
//		t[0].maxsum = -2147483647/2;
		//cerr<<"   p=   "<<p<<endl;
		int &left = t[p].left;
		int &right = t[p].right;
		
		t[p].size = t[left].size + 1 + t[right].size;
		t[p].sum = t[left].sum + t[p].value + t[right].sum;
		/*t[p].maxsum = max(t[left].maxsum,t[left].suf + t[p].value + t[right].pre,t[right].maxsum);
		t[p].maxsum = max(t[p].maxsum,t[left].suf + t[p].value,t[p].value + t[right].pre);*/
		t[p].pre = max(t[left].pre,t[left].sum + t[p].value + t[right].pre,0);
		t[p].suf = max(t[right].suf,t[left].suf + t[p].value + t[right].sum,0);
		
		t[p].maxsum = t[left].suf + t[p].value + t[right].pre;
		
		if(left){
			t[p].maxsum = max(t[p].maxsum,t[left].maxsum);
		} 
		if(right){
			t[p].maxsum = max(t[p].maxsum,t[right].maxsum);
		}
		
//		if(left && right){
//			//cerr<<"1:\n";
//			t[p].maxsum = max(t[p].maxsum,t[left].maxsum,t[right].maxsum);
//			t[p].maxsum = max(t[p].maxsum,t[left].suf + t[p].value + t[right].pre);
//			//cerr<<"t["<<p<<"].maxsum = max("<<t[left].maxsum<<","<<t[left].suf + t[p].value + t[right].pre<<","<<t[right].maxsum<<endl;
//			t[p].maxsum = max(t[p].maxsum,t[left].suf + t[p].value,t[p].value + t[right].pre);
//			//cerr<<"t["<<p<<"].maxsum = max("<<t[p].maxsum<<","<<t[left].suf + t[p].value<<","<<t[p].value + t[right].pre<<endl;
//		}else if(left){
//			//cerr<<"2:\n";
//			//cerr<<"t[left].suf = "<<"t["<<left<<"].suf"<<" = "<<t[left].suf<<endl;
//			t[p].maxsum = max(t[p].maxsum,t[left].maxsum,t[left].suf + t[p].value);
//			//cerr<<"t["<<p<<"].maxsum = max("<<t[left].maxsum<<","<<t[left].suf + t[p].value<<endl;
//		}else if(right){
//			//cerr<<"3:\n";
//			t[p].maxsum = max(t[p].maxsum,t[p].value + t[right].pre,t[right].maxsum);
//			//cerr<<"t["<<p<<"].maxsum = max("<<t[p].value + t[right].pre<<","<<t[right].maxsum<<endl;
//		}
		
//		t[0] = {};
//		int &left = t[p].left;
//		int &right = t[p].right;
//		t[p].size = 1;
//		t[p].sum = t[p].value;
//		t[p].maxsum = t[p].value;
//		if(left){
//			t[p].size += t[left].size;
//			t[p].sum += t[left].sum;
//			t[p].maxsum = max(t[p].maxsum,t[left].maxsum,t[left].suf + t[p].value);
//			if(right){
//				t[p].pre = max(t[left].pre,t[left].sum + t[p].value + t[right].pre,t[left].sum + t[p].value);
//			}else{
//				t[p].pre = max(t[left].pre,t[left].sum + t[p].value);
//			}
////			if(right){
////				t[p].suf = max(t[p].suf,t[left].suf + t[p].value + t[right].sum)
////			}else{
////				t[p].suf = max(t[p].value,t[left].suf + t[p].value);
////			}
//		}
//		if(right){
//			t[p].size += t[right].size;
//			t[p].sum += t[right].sum;
//			t[p].maxsum = max(t[p].maxsum,t[right].maxsum,t[p].value + t[right].pre);
//			if(left){
//				t[p].suf = max(t[right].suf,t[left].suf + t[p].value + t[right].sum,t[p].value + t[right].sum);
//			}else{
//				t[p].suf = max(t[right].suf,t[p].value + t[right].sum);
//			}
//		}
//		if(left && right){
//			t[p].maxsum = max(t[p].maxsum,t[left].maxsum + t[p].value + t[right].maxsum);
//			t[p].pre = max(t[p].pre,t[left].sum + t[p].value + t[right].pre);
//		}
//		cerr<<"t["<<p<<"].maxsum = max("<<t[t[p].left].maxsum<<","<<t[t[p].right].maxsum<<","<<t[t[p].left].suf+t[p].value+t[t[p].right].pre<<")\n";;
//		t[p].pre = max(t[t[p].left].pre,t[t[p].left].sum+t[p].value+t[t[p].right].pre);
//		t[p].suf = max(t[t[p].right].suf,t[t[p].left].suf+t[p].value+t[t[p].right].sum); 
	}//不一定记得在推平后删除翻转标记! 
	void down(int p){
//		if(p==0){
//			return;
//		} 
		
		t[0].clear();
		int &left = t[p].left;
		int &right = t[p].right;
		if(t[p].set != 114514){
			
			if(left){
				t[left].sum = t[left].size * t[p].set;
				t[left].maxsum = max(t[p].set,t[left].sum);
				t[left].pre = max(t[left].sum,0);
				t[left].suf = max(t[left].sum,0);
				t[left].value = t[p].set;
				t[left].set = t[p].set;
//				cerr<<"t["<<left<<"].value="<<t[p].set<<endl;
			}
			if(right){
				t[right].sum = t[right].size * t[p].set;
				t[right].maxsum = max(t[p].set,t[right].sum);
				t[right].pre = max(t[right].sum,0);
				t[right].suf = max(t[right].sum,0);
				t[right].value = t[p].set;
				t[right].set = t[p].set;
//				cerr<<"t["<<right<<"].value="<<t[p].set<<endl;	
			}
			t[p].set=114514;
		}/*else*/ if(t[p].reverse){
			if(left){
				t[left].reverse = !t[left].reverse;
				swap(t[left].left,t[left].right);
				swap(t[left].pre,t[left].suf);
			} 
			if(right){
				t[right].reverse = !t[right].reverse;
				swap(t[right].left,t[right].right);
				swap(t[right].pre,t[right].suf);
			}
			t[p].reverse = false;
		}
		t[0].clear();
	}
	
	void split(int p,int x,int &l,int &r){
		if(!p){
			l=r=0;
			return;
		}
		down(p);
		if(t[t[p].left].size+1<=x){
			l=p;
			split(t[l].right,x-t[t[p].left].size-1,t[l].right,r);
		}else{
			r=p;
			split(t[r].left,x,l,t[r].left);
		}up(p);
	}
	int merge(int l,int r){
		if(!l||!r)return l|r;
		if(t[l].rand<t[r].rand){
			down(l);
			t[l].right=merge(t[l].right,r);
			up(l);
			return l;
		}else{
			down(r);
			t[r].left=merge(l,t[r].left);
			up(r);
			return r;
		}
	}
	
	int create(int x){
		int p=mem.ask();
		t[p].left = t[p].right=0;
		t[p].rand = Rand();
		t[p].size = 1;
		t[p].value = t[p].sum = t[p].maxsum /*= t[p].pre = t[p].suf*/ = x;
		t[p].pre = t[p].suf = max(x,0); 
		t[p].set = 114514;
		t[p].reverse = false;
		return p; 
	}
	void insert(int x){
		root=merge(root,create(x)); 
	}
	void remove(int p){
		if(p==0)return;
		remove(t[p].left);
		mem.remove(p);
		remove(t[p].right);
	}
	void print(int p=root){
		if(!p)return;
		down(p);
		print(t[p].left);
		printf("%d ",t[p].value);
		print(t[p].right);
	}
	
	void insert(int x,int n){
		int pl;
		scanf("%d",&pl);
		int p=create(pl);
		for(int i=2;i<=n;i++){
			scanf("%d",&pl);
			p=merge(p,create(pl));
		}
		int l,r;
		split(root,x,l,r);
		root=merge(merge(l,p),r);
	}
	void remove(int x,int n){
		int l,r;
		split(root,x-1,l,root);
		split(root,n,root,r);
		remove(root);
		root=merge(l,r);
	}
	void reverse(int x,int n){
		int l,r;
		split(root,x-1,l,root);
		split(root,n,root,r);
		t[root].reverse = !t[root].reverse;
		swap(t[root].left,t[root].right);
		swap(t[root].pre,t[root].suf);
		root = merge(merge(l,root),r);
	} 
	void set(int x,int n,int tt){
		int l,r;
		split(root,x-1,l,root);
		split(root,n,root,r);
		t[root].sum = t[root].size * tt;
		t[root].maxsum = max(tt,t[root].sum);
		t[root].pre = max(tt,t[root].sum,0);
		t[root].suf = max(tt,t[root].sum,0);
		t[root].value = tt;
		t[root].set = tt;
		root = merge(merge(l,root),r);
	}
	int sum(int x,int n){
		int l,r;
		split(root,x-1,l,root);
		split(root,n,root,r);
//		up(root);
		int ans=t[root].sum;
		root = merge(merge(l,root),r);
		return ans; 
	}
	int maxsum(){
		return t[root].maxsum;
	}
	int maxsum(int x,int n){
		int l,r;
		split(root,x-1,l,root);
		split(root,n,root,r);
//		cerr<<"::";print(root);cerr<<endl;
//		cerr<<"root="<<root<<endl;
//		cerr<<"----------------------\nup("<<root<<") IS RUNNING!!!!!!\n";
//		up(root);
//		cerr<<"----------------------\nup("<<root<<") ISN'T RUNNING NOW.\n";
		int ans=t[root].maxsum;
//		cerr<<"maxsum("<<x<<","<<n<<"):root="<<root<<endl;
		root=merge(merge(l,root),r);
		return ans;
	}
}t;
main(){
//	freopen("test.in","r",stdin);
//	freopen("test.out","w",stdout);
	
	int n,m;
	scanf("%d %d",&n,&m);
	for(int i=1;i<=n;i++){
		int a;
		scanf("%d",&a);
		t.insert(a);
	}
	while(m--){
		string op;
		int x,n,tt;
		cin>>op;
		if(op=="INSERT"){
			scanf("%d %d",&x,&n);
			t.insert(x,n);
		}else if(op=="DELETE"){
			scanf("%d %d",&x,&n);
			t.remove(x,n);
		}else if(op=="REVERSE"){
			scanf("%d %d",&x,&n);
			t.reverse(x,n); 
		}else if(op=="MAKE-SAME"){
			scanf("%d %d %d",&x,&n,&tt);
			t.set(x,n,tt);
		}else if(op=="GET-SUM"){
			scanf("%d %d",&x,&n);
			printf("%d\n",t.sum(x,n));
		}else if(op=="GET"){
			scanf("%d",&x);
			printf("%d\n",t.sum(x,1));
		}else if(op=="MAX-SUM"){
			scanf("%d %d",&x,&n);
			printf("%d\n",t.maxsum(x,n));
//			t.print();
//			cerr<<endl; 
		}
	}
    
    /*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

P2042 [NOI2005]维护数列

更改 \(N=5\times 10^5\)，并将 .maxsum(x,n) 改为 .maxsum() 即可。

posted @ 2025-07-20 22:37 TH911 阅读(8) 评论(0) 收藏举报

刷新页面返回顶部

TH911 Blog

光阴不可测，岁月亦无歌。