题解：间谍网络

题目传送门

一道水的 提高+/省选−，但是可能会降 普及+/提高。

因为这个请求升 提高+/省选− 的理由是另一道差不多的题目是 提高+/省选−，但是该题已经降 普及+/提高。

$\text{Updated at 2025/7/21}$

真的降 普及+/提高 了……

前置知识

Tarjan 缩点和拓扑排序。

题意分析

有 \(n\) 个间谍，我们可以花费一些金额来收买一些间谍，某些间谍能够控制另外一些间谍，求能否全部控制。若能，求最少花费金额；否则输出编号最小的不能被控制的间谍。

建图

若 \(a\) 能够控制 \(b\)，则在图上连有向边 \(a\to b\)，表示 \(a\) 能控制 \(b\)。

无解的情况

即存在节点不能被控制。

因为我们建图时，像所有能够被控制的节点都连了边，因此我们可以从所有能够被收买的节点开始跑图，能够达到的节点就打上标记代表能控制，最终检查是否有节点没被标记即可。

需要注意，跑图的时候如果跑到了已经标记过的节点，就不再跑了。因为前面能够跑到的节点都已经跑过了。否则时间复杂度可能会被卡成 \(\mathcal O\left(n^2\right)\)。

求最小花费

我们可以将所有的环进行 Tarjan 缩点，环上最小花费代价即新点的花费代价，因为只要从花费最小的点开始，就能够控制整个环上的节点，

因此整个环可以在求解时视为一个整体，考虑缩点。

缩点之后原图就变成了一个有向无环图。

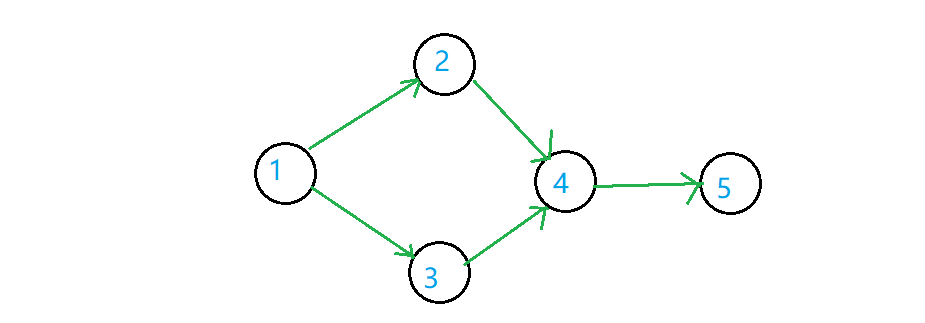
如图中的有向无环图，肯定是从 \(1\) 开始收买最优（也只能从 \(1\) 开始）。

因为从 \(1\) 开始收买就能够控制所有的节点，而从其他节点则不能控制节点 \(1\)，不符合题目要求。

统计答案

因为已经判断过是否有解，因此一定有解，也就是说从新图中所有入度为 \(0\) 的节点开始一定能够控制所有节点。

则直接找出入度为 \(0\) 的节点统计即可。

AC 代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
constexpr const int N=3000,M=8000;
struct graph{
	struct edge{
		int v,r;
	}a[M+1];
	
	int top,n,value[N+1],h[N+1];
	void create(int u,int v){
		a[++top]={v,h[u]};
		h[u]=top;
	}
}old,build;
bool vis[N+1];
void dfs(int x){
	if(vis[x])return;//走过的路不重复走
	vis[x]=true;
	for(int i=old.h[x];i;i=old.a[i].r){
		dfs(old.a[i].v);
	}
}
int dfn[N+1],id[N+1];
void Tarjan(int x){
	static bool flag[N+1];
	static int top,cnt,s[N+1],low[N+1];
	dfn[x]=low[x]=++cnt;
	s[++top]=x;
	flag[x]=true;
	for(int i=old.h[x];i;i=old.a[i].r){
		if(!dfn[old.a[i].v]){
			Tarjan(old.a[i].v);
			low[x]=min(low[x],low[old.a[i].v]);
		}else{
			if(flag[old.a[i].v]){
				low[x]=min(low[x],dfn[old.a[i].v]);
			}
		}
	}
	if(dfn[x]==low[x]){
		build.n++;
		while(s[top]!=x){
			flag[s[top]]=false;
			id[s[top]]=build.n;
			int &valueBuild = build.value[build.n];
			int &valueOld = old.value[s[top]];
			if(!valueBuild)valueBuild=valueOld;
			else if(valueOld)valueBuild=min(valueBuild,valueOld);
			top--;
		}flag[s[top]]=false;
		id[s[top]]=build.n;
		int &valueBuild = build.value[build.n];
		int &valueOld = old.value[s[top]];
		if(!valueBuild)valueBuild=valueOld;
		else if(valueOld)valueBuild=min(valueBuild,valueOld);
		top--;
	}
}
void Build(){
	for(int i=1;i<=old.n;i++){
		for(int j=old.h[i];j;j=old.a[j].r){
			int &u=id[i],&v=id[old.a[j].v];
			if(u==v)continue;
			build.create(u,v);
		}
	}
}
int topSort(){
	static int in[N+1];
	for(int i=1;i<=build.n;i++){
		for(int j=build.h[i];j;j=build.a[j].r){
			in[build.a[j].v]++;
		}
	}
	int ans=0;
	for(int i=1;i<=build.n;i++){
		if(!in[i]){
			ans+=build.value[i];
		}
	}return ans;
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	int p;
	scanf("%d %d",&old.n,&p);
	for(int i=1;i<=p;i++){
		int x,y;
		scanf("%d %d",&x,&y);
		old.value[x]=y;
	}
	int r;
	scanf("%d",&r);
	while(r--){
		int a,b;
		scanf("%d %d",&a,&b);
		old.create(a,b);
	}for(int i=1;i<=old.n;i++){
		if(old.value[i])dfs(i);
	}for(int i=1;i<=old.n;i++){
		if(!vis[i]){
			printf("NO\n%d\n",i);
			return 0;
		}
	}for(int i=1;i<=old.n;i++){
		if(!dfn[i])Tarjan(i);
	}Build();
	printf("YES\n%d\n",topSort());
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}