题解：中位数

题目传送门

权值树状数组

很好理解，\(i\) 枚举 \(1\sim n\)，每次往权值状数组中加入 \(a_i\)，这样我们就能知道对于一个数 \(x\)，\(a[1...i]\) 中小于等于 \(x\) 的数的个数。

• 二分答案，在值域上二分第 \(k\) 大的数，时间复杂度，\(\mathcal O(n\log^2 n)\)。

• 倍增查询最大的 \(pl\) 使得 \(a[1...i]\) 中有 \(k-1\) 个数小于等于 \(pl\)，\(pl+1\) 即第 \(k\) 大的数。

  时间复杂度：\(\mathcal O(n\log n)\)。

参考代码

//#include<bits/stdc++.h>
#include<algorithm> 
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
const int N=100000;
int n,m,a[N+1],b[N+1],c[N+1];
int lowbit(int x){
	return x&-x;
}
void add(int x,int k){
	while(x<=m){
		c[x]+=k;
		x+=lowbit(x);
	}
}
//倍增查询
int query(int k){
	int cnt=0,pl=0;
	for(int i=1<<20;i>0;i/=2){
		pl+=i;
		if(pl>m||cnt+c[pl]>=k)pl-=i;
		else cnt+=c[pl];
	}return pl+1;
}
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",a+i);
		b[i]=a[i];
	}sort(b+1,b+n+1);
	m=unique(b+1,b+n+1)-b-1;
	for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+n+1,a[i])-b;
	for(int i=1;i<=n;i++){
		add(a[i],1);
		if(i%2)printf("%d\n",b[query((i+1)/2)]);
	}
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

权值线段树

这也是此处的方法，考虑到此方法复杂、代码冗长、常数较大，此处不予代码。

事实上，与上一种方法几乎一模一样，区别仅仅在于将树状数组改为线段树。

对顶堆

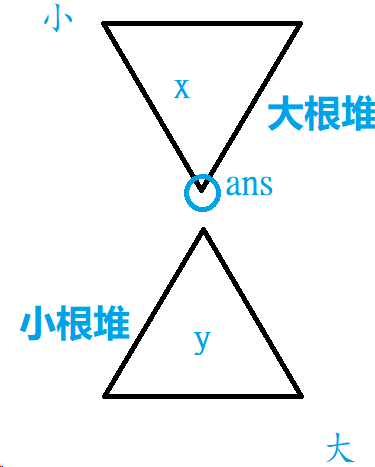
我们维护一个大根堆 \(x\) 和一个小根堆 \(y\)，让 \(x\) 中的元素小于 \(y\) 中的元素，即 \(x.top()<y.top()\)。

每次插入元素 \(a_i\) 时，若 \(a_i \leq x.top()\)，则将 \(a_i\) 加入 \(x\)，否则将 \(a_i\) 加入 \(y\)。

而答案即调整 \(x,y\) 的元素数量，使得 \(x.size()=y.size()+1\)，此时 \(x.top()\) 即答案。

---

其实堆可以说是一个弱化版的排序，而数据结构的本质就是不去处理不需要的信息（比如懒标记、堆），因此复杂度得以提升。

时间复杂度：\(\mathcal O(n\log n)\)。

参考代码

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
int n,pl;
priority_queue<int>x;
priority_queue<int,vector<int>,greater<int> >y;
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	scanf("%d",&n);
	scanf("%d",&pl);
	x.push(pl);
	printf("%d\n",pl); 
	for(int i=2;i<=n;i++){
		scanf("%d",&pl);
		if(pl>x.top())y.push(pl);
		else x.push(pl);
		while(y.size()>x.size()){
			x.push(y.top());
			y.pop();
		}
		while(x.size()>y.size()+1){
			y.push(x.top());
			x.pop();
		}
		if(i%2)printf("%d\n",x.top());
	}
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

插入排序

这是个什么鬼方法......数据过水（

声明：本方法时间复杂度为 \(\mathcal O\left(n^2\right)\)，但因为常数较小且数据过水，可以通过此题。

依题意模拟进行插入排序即可。

插入时间复杂度：\(\mathcal O(n)\)。

以下代码使用二分求出了应该插入的位置，然而还是 \(\mathcal O(n)\)。

参考代码（数组）

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
int n,pl;
int a[100001];
void insert(int x,int p,int size){
	for(int i=size+1;i>=p;i--)a[i+1]=a[i];
	a[p]=x;
} 
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&pl);
		insert(pl,upper_bound(a,a+i,pl)-a,i-1);
		if(i%2){
			printf("%d\n",a[i/2+1]);
		}
	}
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}

参考代码（vector）

//#include<bits/stdc++.h>
#include<algorithm>
#include<iostream>
#include<cstring>
#include<iomanip>
#include<cstdio>
#include<string>
#include<vector>
#include<cmath>
#include<ctime>
#include<deque>
#include<queue>
#include<stack>
#include<list>
using namespace std;
int n,pl;
vector<int>a;
int main(){
	/*freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);*/
	
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&pl);
		a.insert(upper_bound(a.begin(),a.end(),pl),pl);
		if(i%2){
			printf("%d\n",a[a.size()/2]);
		}
	}
	
	/*fclose(stdin);
	fclose(stdout);*/
	return 0;
}