(笔记)决策单调性 四边形不等式优化 WQS 二分 Slope Trick
文中所有图片引用来自【学习笔记】WQS二分详解及常见理解误区解释。
学了,但是没学明白,再学一遍。花一晚上没写题,整理这些东西。
WQS 二分
用于解决一类问题:
给定 \(n\) 个物品,要求恰好选 \(m\) 个,最大化/最小化选择物品的权值和(下文称为最优答案)。
使用条件:令 \(g(i)\) 表示恰好选择 \(i\) 个的最优答案,则点集 \((i,g(i))\) 拟合图形为一个凸包(上凸包/下凸包)。显然,我们要求的东西就是 \(g(m)\)。重要性质是随着额外权值 \(k\) 的递增,相应最优选择次数递增或递减,此性质与凸包模型互为充要条件。
朴素思路
显然这个东西可以直接背包做到 \(O(nm)\),具体方法可以令 \(f(i,j)\) 表示前 \(i\) 个,选了 \(j\) 次的最优答案,有转移 \(f(i,j)=\max / \min f(k,j-1)+cost(k,i)\)。但是我们不能止步于此,用 WQS 二分就可以优化到 \(O(n\log V)\)。
算法内容
我们画出这个凸包:
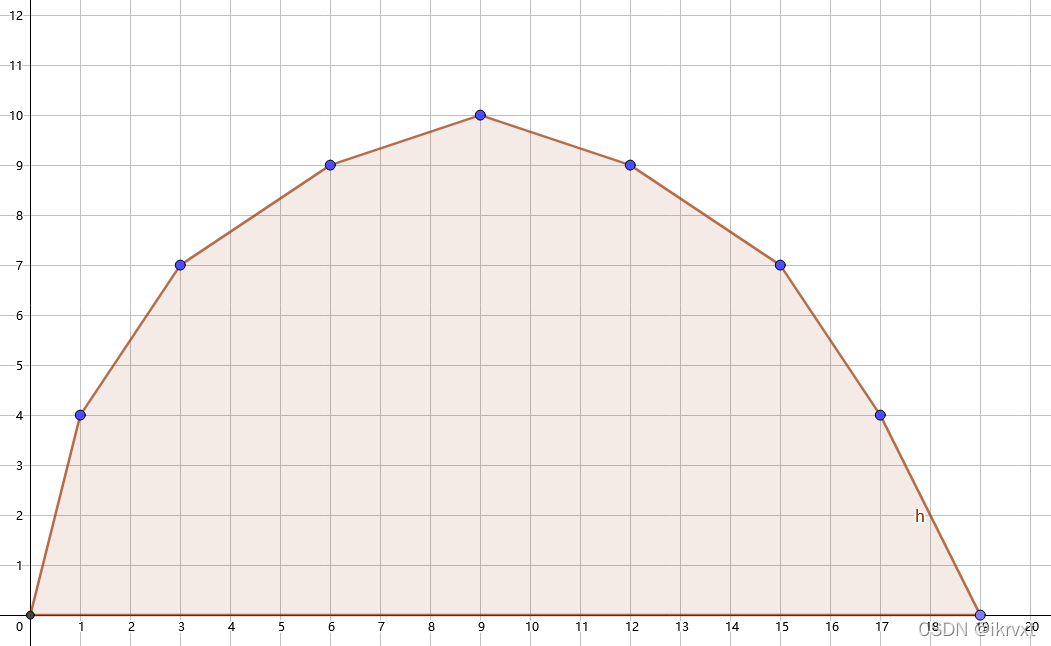
我们的算法所做的东西就是用一条斜率为 \(k\) 的直线不停地截这个凸包,\(\text{check(k)}\) 函数做的就是找到我们能截到的那个最值(截距的最值)。
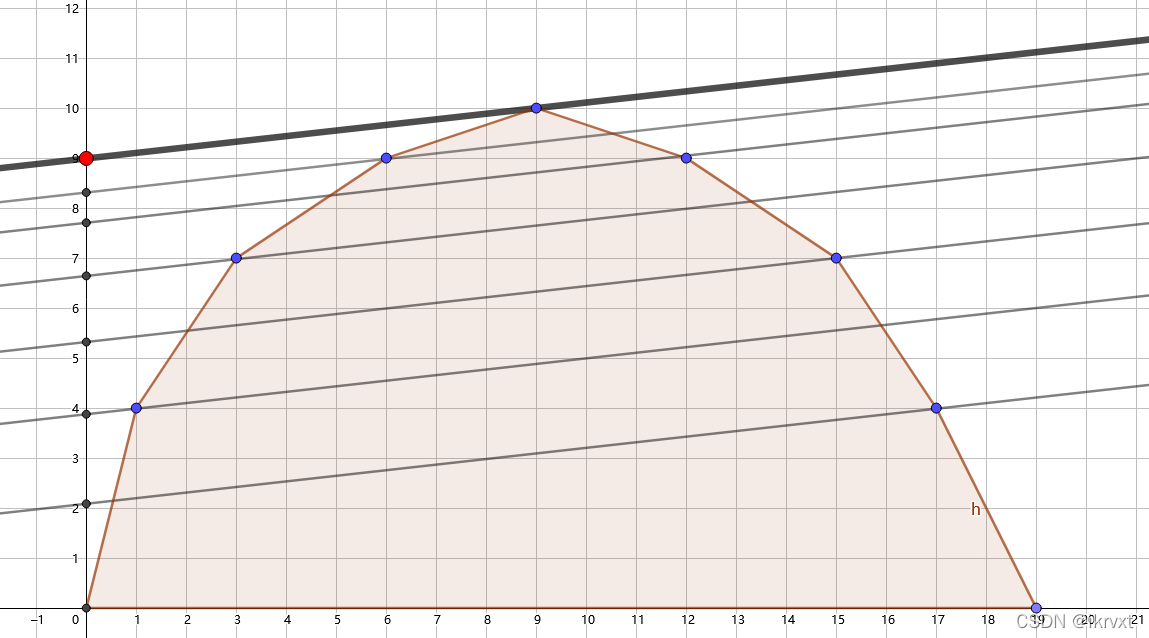
这是一种类比。具体来说,你需要在每次多选一次时加一个额外权值 \(k\) 即斜率,这个东西的大小可以随意调控,然后让 \(\text{check(k)}\) 告诉你它的最优解选择了几个物品,根据这个返回值调整输入的 \(k\)。然后你最终得到的答案其实就是 \(b(m)=g(m)-km\),这就契合了我们的直线截凸包形式,类似的思路在(笔记)斜率优化 DP 李超线段树
可见一斑。
然后其实就完成了算法的主体内容。每次二分会告诉你截到的截距和点横坐标,你只需要在二分外层调整斜率 \(k\) 截到 \(x=m\) 的最优解即可。
算法细节
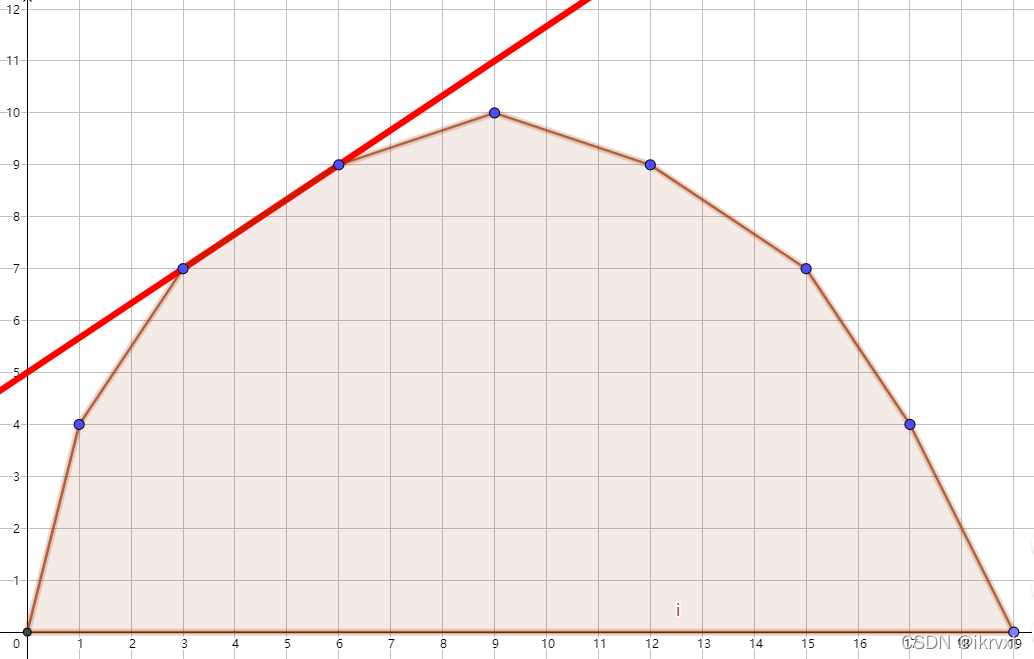
最终答案我们需要加上 \(km\) 而不是 \(k\times\) 二分实际选择的 \(x\)。
这其实是个比较简单的思维问题,不需要多少文字来描述。在实际情况中,我们可能遇到这种东西:上面这条直线切了 \(x=3,4,5,6\) 这四个点,再假设 \(m=4\text{ or }5\),你的二分在标准写法下应该找到的是左端点 \(x=3\) 或右端点 \(x=6\),但是你实际上要找的答案 \(g(m)=b(m)+km\),这个 \(b(m)\) 是你求出来的,而且作为截距,它和 \(b(3),b(4),b(5),b(6)\) 都是一样的,但是你的 \(m\) 可能是不同的。然后就解决了为什么要加的东西是 \(km\) 了。
WQS 二分的精髓重在理解与模型猜想(构造)。前提是这是一种凸包,然后就可以简单地进行优化把一维变成 \(\log\) 级别的,真正写起来其实并不难。
决策单调性 四边形不等式优化 DP
一般化地,我们要解决以下问题:
对于 \(i\),取得的最优值 \(f(i)\) 称为状态 \(f(i)\),问题 \(i\) 中在 \(j\) 的取值 \(w(j,i)\) 称为决策 \(j\),记最小最优决策点为 \(opt(i)\)。
- 决策单调性:\(\forall i_1<i_2\),有 \(opt(i_1)\le opt(i_2)\)。
- 四边形不等式:\(\forall a\le b\le c\le d\),有费用函数 \(w(a,c)+w(b,d)\le w(a,d)+w(b,c)\)。
(交叉小于包含)
Theorem 1:对于满足四边形不等式的 \(w\),它一定满足决策单调性。
Proof:采用反证法,证明不存在任意一个同时不满足决策单调性且满足四边形不等式的 \(w\)。具体推理见 OI-wiki。
分治优化
对于问题 \(i\rightarrow[l,r]\),先 \(O(n)\) 求出 \(opt(i/2)\),然后递归 \([l,mid-1],[mid+1,r]\)。根据决策单调性,其中左区间的 \(opt\) 上限为 \(opt(i/2)\),右区间 \(opt\) 下限为 \(opt(i/2)\)。这样不断限制可以使每层的总时间为 \(O(n)\),\(O(n\log n)\) 的总时间复杂度。
二分队列优化
这类问题的转移是二维的:
Theorem 2:对于满足四边形不等式的 \(w\),一定有满足四边形不等式的 \(f(k,i)\)。
证明繁杂,略。
Theorem 3:\(opt(i-1,j)\le opt(i,j)\le opt(i,j+1)\)。
证明略。第二个不等式就是决策单调性。第一个由 Theorem 2 可得。
对于每个决策 \(j\),寻找它最优的问题区间 \([l_j,r_j]\)。怎么快速地算出这些东西?单调队列+二分可以做到。\(i\) 表示当前加入的决策点(同时也代表我们当前处理到的问题),我们的过程是这样的:
- 初始出队:把队头每个 \(r<i\) 的决策扔掉。
- 计算答案(最优解在队头)。
- 入队:假设要加入决策 \(j\),替换队尾决策 \(j'\),讨论一些情况。对于问题 \(l_{j'}\) 来说,如果 \(j\) 更优或贡献相同,那么对于比 \(i\) 更靠后的问题,更优决策点肯定在后面,所以可以直接
pop掉队尾。此时如果队列空了,入队 \((j,j+1,n)\)。非空那么就会处于这么一个状态:\(j\) 在 \(l_{j'}\) 严格劣于 \(j'\),但在 \(r_{j'}\) 非严格优于 \(j'\)(可以取等)。这时就可以用二分找到第一个满足 \(j\) 非严格优于 \(j'\) 的问题作为加入决策的左边界,更新队尾的有边界。
结合上面的 WQS 二分可以去掉一维,再用决策单调性(二分队列)优化转移,就可以做到 \(O(n\log n\log C)\)。
代码实现如下:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=5e5+5;
int n,m,a[N];
LL pre[N],f[N],cnt[N];
LL w(int i,int j){
int mid=(i+j)/2;
int lsiz=mid-i+1;
int rsiz=j-mid;
return 1ll*lsiz*a[mid]-(pre[mid]-pre[i-1])+(pre[j]-pre[mid])-1ll*rsiz*a[mid];
}
LL ant;
LL val(int j,int i){
return f[j-1]+w(j,i)+ant;
}
int q[N],hd=1,tl;
int lt[N],rt[N];
int check(){
for(int i=1;i<=n;i++)f[i]=0,cnt[i]=0;
hd=1,tl=0;
for(int i=1;i<=n;i++){
while(hd<=tl&&rt[q[hd]]<i)hd++;
if(hd<=tl)lt[q[hd]]=i;//如果该决策点到 i 才被访问,说明在 1~i-1 时它都不是最优决策点。
while(hd<=tl&&val(i,lt[q[tl]])<=val(q[tl],lt[q[tl]]))
tl--;
if(hd>tl){
lt[i]=i;
rt[i]=n;
q[++tl]=i;
}
else if(val(i,rt[q[tl]])<=val(q[tl],rt[q[tl]])){
int l=lt[q[tl]],r=rt[q[tl]],res=rt[q[tl]];
while(l<=r){
int mid=(l+r)>>1;
if(val(i,mid)<=val(q[tl],mid))res=mid,r=mid-1;//res 记录第一个满足 i 可以完全替换 q[tl] 的位置。
else l=mid+1;
}
rt[q[tl]]=res-1;
lt[i]=res;
rt[i]=n;
q[++tl]=i;
}
else if(rt[q[tl]]<n){
lt[i]=rt[q[tl]]+1;
rt[i]=n;
q[++tl]=i;
}
f[i]=val(q[hd],i);
cnt[i]=cnt[q[hd]-1]+1;
}
return cnt[n];
}
LL ans;
void solve(){
LL l=0,r=2e12;
while(l<=r){
LL mid=(l+r)>>1;
ant=mid;
int pmid=check();
if(pmid>=m)ans=mid,l=mid+1;
else r=mid-1;
}
ant=ans;check();
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
sort(a+1,a+1+n);
for(int i=1;i<=n;i++)
pre[i]=pre[i-1]+a[i];
solve();
printf("%lld",f[n]-m*ans);
return 0;
}
Slope Trick
待更新。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号