(笔记)斜率优化 DP 李超线段树
下午没什么事,听 Lgx_Q 神犇的课又听不懂,遂补个 blog。
斜率优化 DP
单调队列维护凸包
这是一类较为经典的 DP 优化问题。
具体来说,它们都具有这样的转移形式:
它的转移里面有一项和 \(i,j\) 都有关。处理这类问题的方式就是先把 \(\min\)(或者 \(\max\))拆掉,然后把 \(j\) 看成是常数,式子整理成 \(y=kx+b\) 的形式,\(b,k\) 只和 \(i\) 有关,\(y,x\) 只和 \(j\) 有关。这样我们要求的 \(f_i\) 就一定在 \(b=y-kx\) 里面,令该值最大/最小化即可。这就是斜率优化 DP 截距的来源。
每次转移的时候,只需要在某种结构里面记录 \((x,y)\),然后找出当前对应 \(k\) 下最大化/最小化的截距 \(b\) 即可。
具体来说,如果 \(b_j\) 具有单调性,那么仍可以用单调队优化,每次记录 \((x,y)\) 往队尾(或队头)丢个值即可。甚至于当 \(k\) 不单调时,你也可以通过在单调队列上二分找出最优解。
但是万一 \(b_j\) 也不单调,这时你就老实了,这里我们下文会介绍一种解决方法叫李超线段树,在 \(O(n\log n)\) 的时间内解决这个问题。
例题
转移:
这里容易观察到 \(A_i,B_j\) 都具有单调性,我们考虑找最优决策点。我们存下来的 \((x,y)\) 点集应该构成一个凸包,在这里我们每次在队尾加入点,每次改变斜率 \(k\) 去截这个凸包上的点,要使截出来的截距最大化。
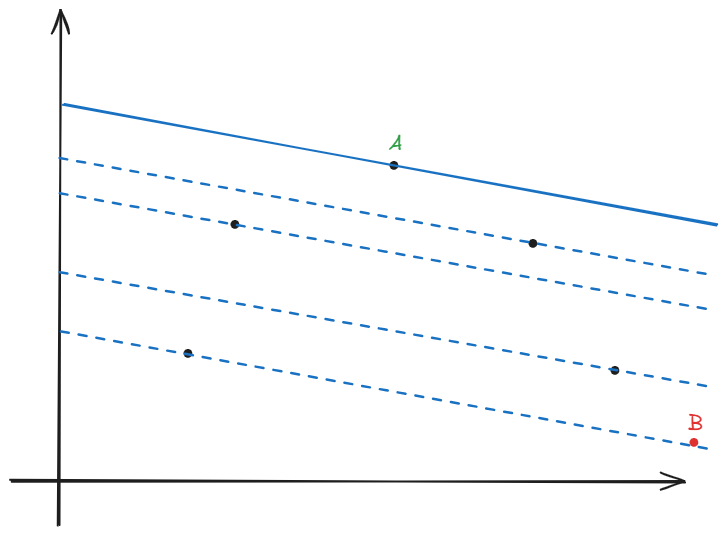
这是上凸包的形态。
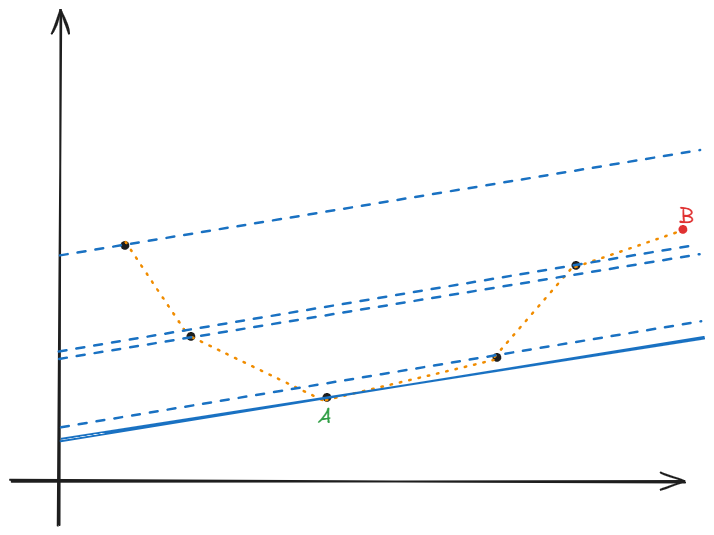
这是下凸包的形态。
直线斜率(正)递增,所以动态处理应该是不停在逆时针旋转的。我们要取到的是最优决策点 \(A\),为了让接下来的决策也能取到可能的最优决策点,我们维护一个下凸包。截到的最优的点 \(A\),想象一下,一定在该凸包与直线的斜率拟合处。由于斜率(正)递增,有些队列前面的节点永远取不到了,这时候我们可以把队头的一些没用的节点扔掉,这些节点比它们右边的节点截出来的东西严格更劣。那就变成了这样:
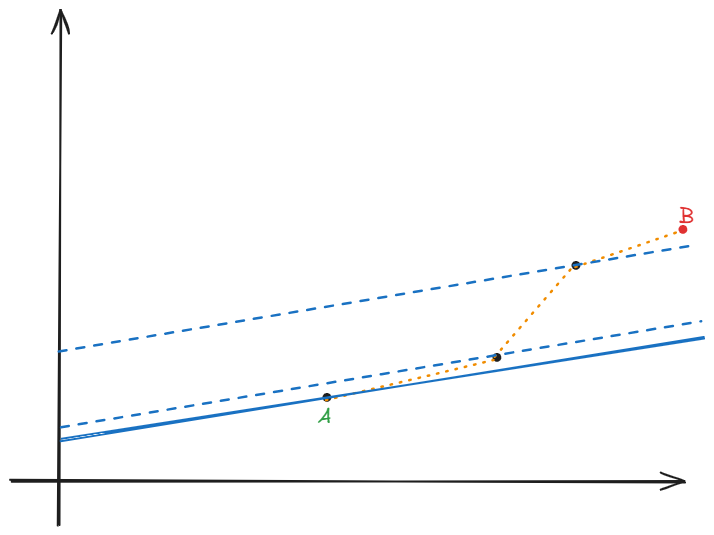
然后我们再考虑在队尾插入一些节点,这些都建立在单调性的基础上。如插入一个节点 \(B\),我们需要不断地扔掉队尾的点直到加入节点 \(B\) 不会破坏下凸包。为什么这样是对的?考虑我们加入 \(B\) 破坏了下凸包结构的状态,那么此时直线拟合到队尾那个点的时候决策一定更劣(感性理解)。再者,如果发生冲突,为什么不能保留队尾而是要保留最新的 \(B\)?因为对于到达那里的直线,截取 \(B\) 一定要比截取旧队尾要更优。
代码实现:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL,LL> PII;
const int N=5e4+5;
LL n,L,c[N],pre1[N],pre2[N];
struct dq{
PII val[N];
int hd=1,tl;
void push(PII a){val[++tl]=a;}
void pop_back(){tl--;}
void pop_front(){hd++;}
int siz(){return tl-hd+1;}
PII front(){return val[hd];}
PII back(){return val[tl];}
PII sfront(){return val[hd+1];}
PII sback(){return val[tl-1];}
}q;
LL dp[N];
LL gt(PII a,LL k){return a.second-k*a.first;}
bool cmp(PII a,PII b,LL k){return gt(a,k)>=gt(b,k);}
bool bet(PII a,PII b,PII c){
return 1.0*(b.second-a.second)*(c.first-a.first)>1.0*(c.second-a.second)*(b.first-a.first);
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>L;
for(int i=1;i<=n;i++){
cin>>c[i];
c[i]+=c[i-1];
pre1[i]=c[i]+i;
pre2[i]=c[i]+i+L+1;
}
q.push(make_pair((L+1),(L+1)*(L+1)));
for(int i=1;i<=n;i++){
while(q.siz()>=2&&cmp(q.front(),q.sfront(),2*pre1[i]))q.pop_front();
dp[i]=gt(q.front(),2*pre1[i])+pre1[i]*pre1[i];
PII id=make_pair(pre2[i],pre2[i]*pre2[i]+dp[i]);
while(q.siz()>=2&&bet(q.sback(),q.back(),id)){
q.pop_back();
}
q.push(id);
}
cout<<dp[n];
return 0;
}
李超线段树
解决的是在平面直角坐标系中,加入一些线段 \(y=kx+b(x\in [A,B])\),然后询问 \(x\in[A,B]\) 中取到的 \(y\) 最大/最小值是多少。基本思想是用线段树来拆开找到查询/修改的所有完整子区间,然后再在这些区间里面操作。具体地,每个区间都标上一个编号为 \(tg_p\) 的线段,表示在节点 \(p\) 所代表的区间 \([l,r],mid=\lfloor\frac{l+r}{2}\rfloor\) 中 \(x=mid\) 取到的 \(y\) 最大值。如果我们丢进来一条线段,找到一个空节点 \(tg_p=0\),就直接挂在 \(tg_p\) 上。如果它在 \(x=mid\) 的时候比原线段更劣,那我们考虑这两个线段的交点在哪里。如果在左区间就往左区间递归,反之亦然。如果都不在,说明被完全偏序了,直接丢掉即可。如果更优,那么直接进行 \(tg_p\) 和新线段的交换,然后把原来的 \(tg_p\) 当作更劣情况继续递归,时间复杂度 \(O(n\log^2n)\)。
具体地,在斜率优化一类问题中,我们不用分割这些区间,而是直接在全局上做,不用考虑线段端点的问题,所以时间复杂度是 \(O(n\log n)\)的。我们的具体应用是把加入的点 \((x,y)\) 中 \(-x\) 当作斜率,\(y\) 当作截距,\((k,b)\) 作为取到的值与对应点值。这个应用和单调队列优化是相反的,但是更加自然。
这里给出模板题 P4097 【模板】李超线段树 / [HEOI2013] Segment 的代码实现:
#include<bits/stdc++.h>
typedef double LD;
using namespace std;
const int N=1e5+10;
const int mod=39989,MOD=1e9;
int n,op,lst;
const LD eps=1e-9;
struct Seg{
LD k,b;
LD val(int x){
return 1.0*k*x+1.0*b;
}
}s[N];
Seg Sg(int xa,int ya,int xb,int yb){
Seg ans;
if(xa==xb){
ans.k=0;
ans.b=1.0*max(ya,yb);
}
else {
ans.k=(yb-ya)*1.0/(xb-xa);
ans.b=ya-1.0*ans.k*xa;
}
return ans;
}
int cmp(LD x,LD y){
if(y-x>eps)return 0;
if(x-y>eps)return 1;
return 2;
}
int mx(int x,int y,int v){
int op=cmp(s[x].val(v),s[y].val(v));
if(op==2)return (x<y?x:y);
return (op ? x : y);
}
int idx;
struct Sgt{
#define ls (p<<1)
#define rs (p<<1|1)
#define mid ((l+r)>>1)
int tg[N<<2];
void update(int p,int l,int r,int val){
if(!tg[p]){tg[p]=val;return ;}
if(mx(tg[p],val,mid)==val)swap(tg[p],val);
if(l==r)return ;
if(mx(tg[p],val,l)==val)update(ls,l,mid,val);
if(mx(tg[p],val,r)==val)update(rs,mid+1,r,val);
}
void fids(int p,int l,int r,int L,int R,int val){
if(L<=l&&r<=R){update(p,l,r,val);return ;}
if(L<=mid)fids(ls,l,mid,L,R,val);
if(R>mid)fids(rs,mid+1,r,L,R,val);
}
int que(int p,int l,int r,int x){
if(l==r)return tg[p];
if(x<=mid)return mx(tg[p],que(ls,l,mid,x),x);
else return mx(tg[p],que(rs,mid+1,r,x),x);
}
#undef ls
#undef rs
#undef mid
}T;
const int siz=39990;
signed main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n;
while(n--){
cin>>op;
if(op){
int xa,xb,ya,yb;
cin>>xa>>ya>>xb>>yb;
xa=(xa+lst-1)%mod+1;
ya=(ya+lst-1)%MOD+1;
xb=(xb+lst-1)%mod+1;
yb=(yb+lst-1)%MOD+1;
if(xa>xb)swap(xa,xb),swap(ya,yb);
s[++idx]=Sg(xa,ya,xb,yb);
T.fids(1,1,siz,xa,xb,idx);
}
else {
int k;
cin>>k;
k=(k+lst-1)%mod+1;
lst=T.que(1,1,siz,k);
cout<<lst<<'\n';
}
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号