概述
通常支持向量机用于分类,如下图中两类点。
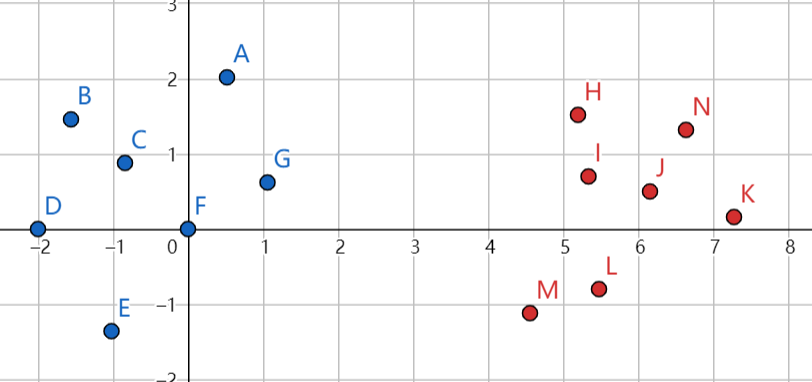
显然,可以正确分类的直线有很多,如紫色的直线和灰色的直线,但是在测试时,紫色的直线更不容易出错,我们希望支持向量机找的就是这类超平面。
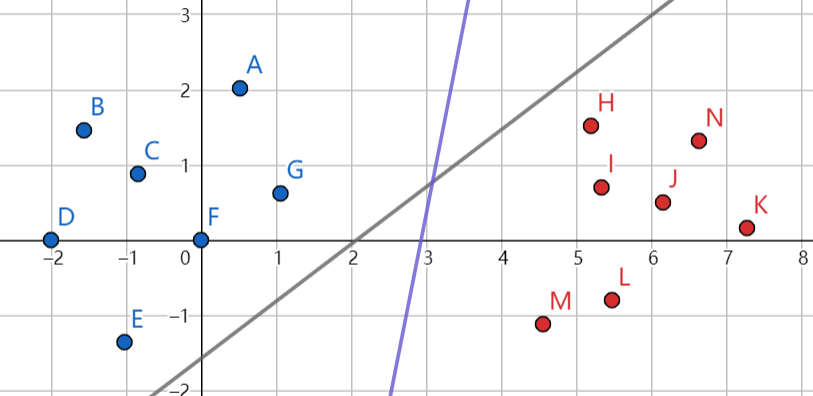
线性可分
线性可分和线性不可分很好理解,顾名思义,在某些情况下由于噪声的影响,本来两类互不交叉的点混到一起了。
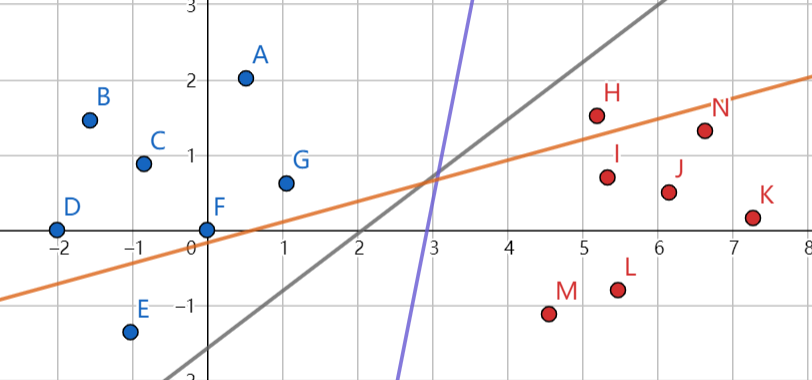
我们需要找的是图中紫色的线。它的特征就是两侧(类)点中到它距离最近的点距离最远。
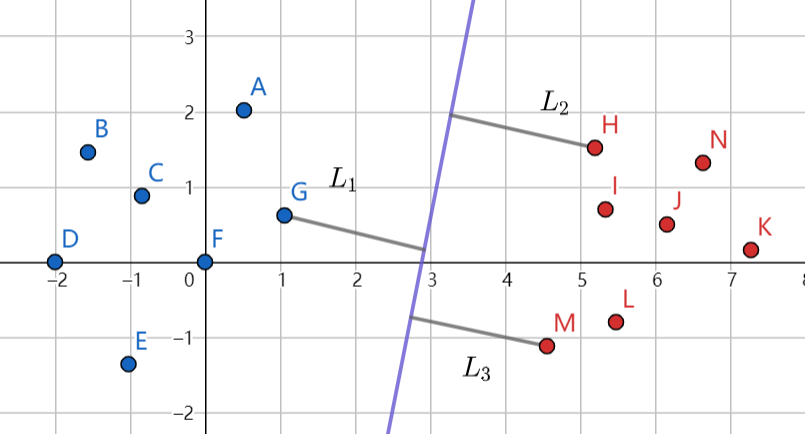
图中距离较远的点,对这个平面没有影响,我们称这些有影响的点,也就是距离最近的点,为支持向量(G、H、M)。
\(x\)形如\(\begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix}\),\(w\)形如\(\begin{bmatrix} w_1 \\ w_2 \\ \vdots \\w_n \end{bmatrix}\)
定义:
\[y^i(w^T x^i + b)
\]
\[\frac{y_i(w^T x^i + b)}{||w||_2}
\]
现在我们要做的,其实就是最大化几何距离,这样在线性可分情况下就可以最大化两类点到超平面的最小距离。
即
\[\max_{w, b} \frac{y^i(w^T x^i + b)}{||w||_2}
\]
由于我们最大化的是最小距离,所以可以规定一个最小的距离限制\(\lambda '\),一般取1即可。
\[\max_{w,b} \frac{1}{||w||_2}\\
\text{s.t. } y^i (w^T x^i + b) \geq 1
\]
等价于
\[\min_{w,b} \frac{1}{2}||w||^2_2\\
\text{s.t. } y^i (w^T x^i + b) \geq 1 \tag{2.1}
\]
拉格朗日乘子法
\[\min_{x} f(x)\\
\text{s.t. } g_i(x) = 0 \quad i=0, 1, 2\dots n
\]
构造拉格朗日函数
\[L(x, \alpha) = f(x) + \sum_i \alpha_i g_i(x)
\]
计算\(\min_{x, \alpha} L(x, \alpha)\)
\[\frac{\partial L}{x_i} = 0 \quad i=0,1,2\dots n\\
\frac{\partial L}{\alpha_i} = 0 \quad i=0,1,2\dots m
\]
\[\min_{x, y} x^2 + y^2\\
\text{s.t. } xy = 3
\]
构造拉格朗日函数
\[L = x ^2 + y^2 + \alpha (xy - 3)
\]
\[\left \{
\begin{matrix}
\frac{\partial L}{\partial x} = 2x+\alpha y = 0\\
\frac{\partial L}{\partial y} = 2y + \alpha x = 0\\
\frac{\partial L}{\partial \alpha} = xy - 3 = 0
\end{matrix}
\right .
\]
解得\(
\left \{ \begin{matrix}
x = \sqrt{3}\\
y = \sqrt{3}
\end{matrix} \right .\) 或 \(\left \{ \begin{matrix}x = -\sqrt{3}\\y = -\sqrt{3}\end{matrix} \right .\)
对于含有不等条件的约束
\[\begin{align}
& \min_{x}f(x)\\
\text{s.t. } & g_i(x) = 0 \quad i=0,1,2\dots\\
& h_i(x) \leq 0 \quad i=0,1,2\dots
\end{align} \tag{2.2}
\]
构造拉格朗日函数
\[L(x, \alpha, \beta) = f(x) + \sum_i \alpha_i g_i(x) + \sum_j \beta_j h_i(x)\\
\beta_j \geq 0 \quad j=1,2\dots
\]
若两个约束是可行的
\[\max_{\alpha, \beta} L(x, \alpha, \beta) = \left \{ \begin{matrix}
f(x) & \text{满足约束}\\
\infty & \text{otherwise}
\end{matrix} \right .
\]
所以\(\max_{\alpha, \beta} L(x, \alpha, \beta) = f(x)\),原始问题的解可以通过求解对偶问题得到
\[\min_{x} \max_{\alpha, \beta} L(x, \alpha, \beta)
\]
在满足slater条件下,原始问题的解和对偶问题的解是等效的,即\(\min_{x} \max_{\alpha, \beta} L(x, \alpha, \beta)\)和\(\max_{\alpha, \beta} \min_{x} L(x, \alpha, \beta)\)有相同的解\(\hat x\)
现在我们去求解\((2.1)\)式。
构造拉格朗日函数
\[\begin{align}L(w, b, \alpha, \beta) = & \frac{1}{2}||w||^2 + \sum_i \alpha_i (1 - y^i (w^T x^i + b))\\\text{s.t. } & \alpha_i \geq 0\\& 1 - y^i (w^T x^i + b) \leq 0\end{align} \tag{2.2}
\]
\[\frac{\partial L}{\partial w} = w - \sum_i \alpha_i x^i y^i = 0\\\frac{\partial L}{\partial b} = -\sum_i \alpha_i y^i = 0 \tag{2.3}
\]
将\((2.3)\)代入\((2.2)\)
\[\min_{w, b} L(w,b,\alpha) = \min_{w, b} -\frac{1}{2}\sum_i \sum_j \alpha_i \alpha_j y^i y^j {x^i}^{T} x^j + \sum_i \alpha_i \tag{2.4}
\]
对\((2.4)\)求关于\(\alpha\)的最大值过程可以使用SMO算法。
假设最优值已经解出
\[\hat w = \sum_i \alpha_i y^i x^i \tag{2.5}
\]
由\((2.5)\)可以观察出,只有\(\alpha_i \neq 0\)的点,\(x^i, y^i\)才对\(w\)的值有影响,这些点我们称为支持向量。
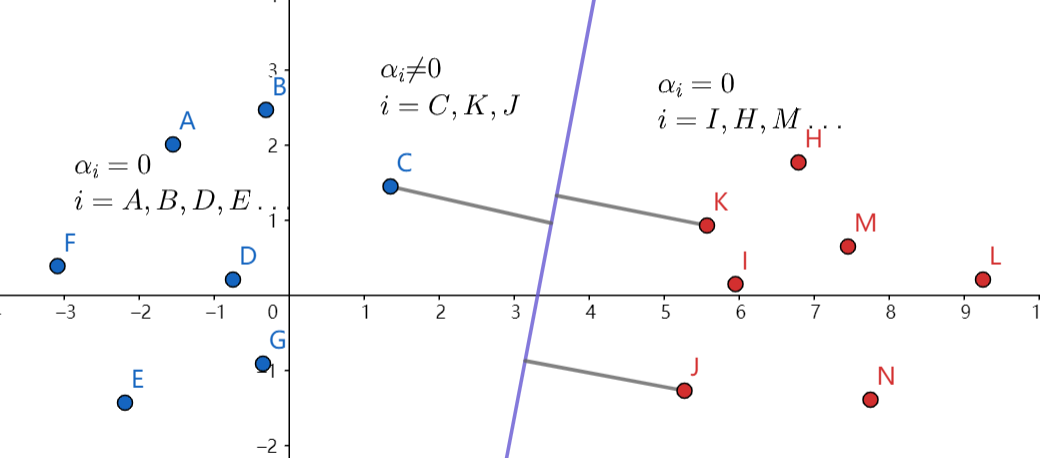
线性不可分
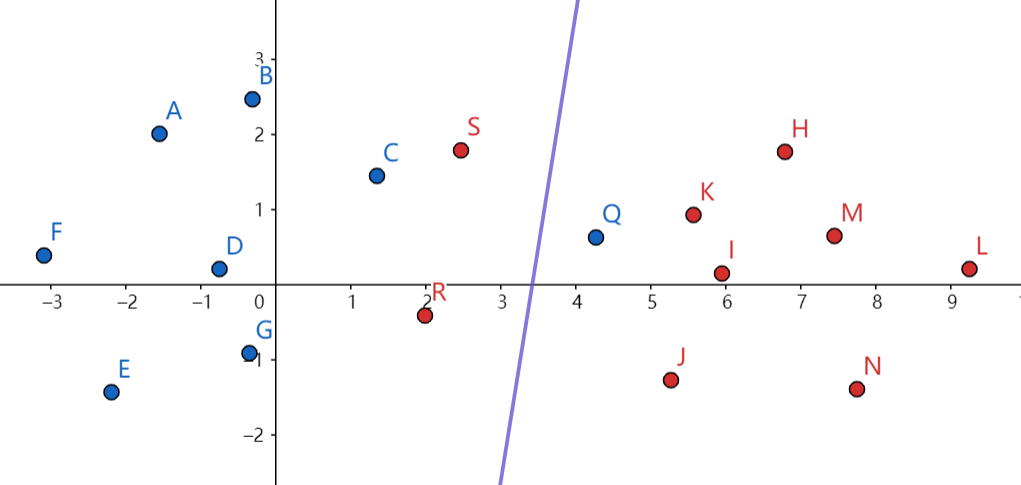
如图这样的数据点分布就是线性不可分的。
我们定义如下函数来作为错误分类的量化值。
\[\xi_i = \max (0, 1-y^i (w^T x^i + b))
\]
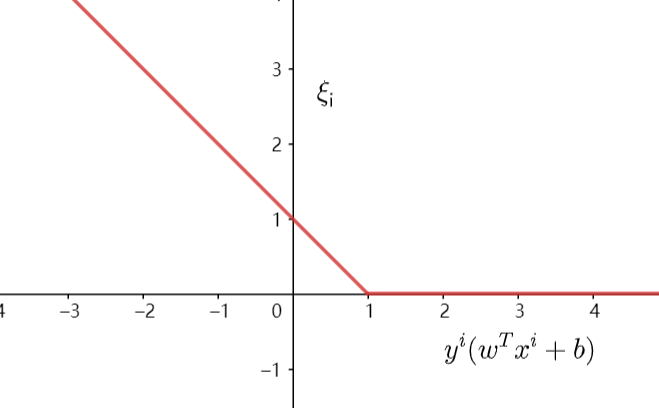
\[\begin{align}& \min \frac{1}{2}||w||^2 + C \sum_i \xi_i\\\text{s.t. } & \xi_i \geq 0\\& \xi_i \geq 1 - y^i(w^T x^i + b)\end{align}
\]
构造拉格朗日函数
\[L(w, b, \alpha, \beta, \xi) = \frac{1}{2}||w||^2 + C\sum_i \xi_i + \sum_i \alpha_i (-\xi_i+1-y^i(w^Tx^i + b)) - \sum_i \beta_i \xi_i
\]
求解方法和线性可分情况下是一样的。
其中不同参数情形请参考下图。

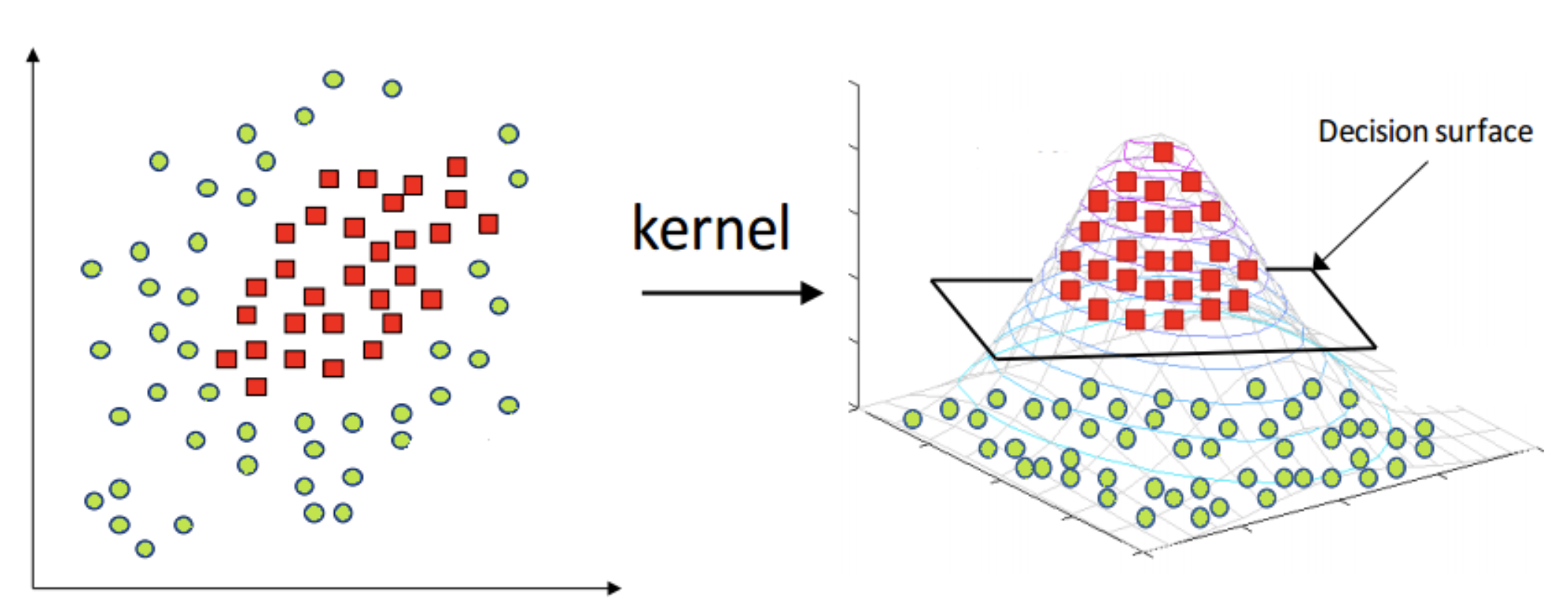
非线性分类
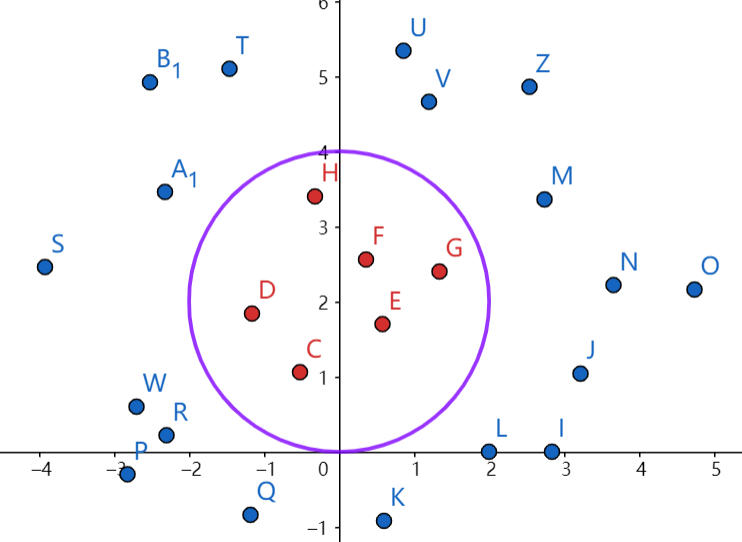
如图是线性不可分的数据,但是这样一个圆可以把数据分的很好。
虽然没办法直接用线性平面将两类点分开,但是只要对数据做一个映射,就变得可分了。
\[\begin{pmatrix} x \\ y \end{pmatrix} \rightarrow \begin{pmatrix} x^2 \\ (y-2)^2 \end{pmatrix}
\]
核函数
设\(X\)是输入空间,\(H\)是特征空间,如果存在一个\(X\)到\(H\)的映射
\[\phi(x):X \rightarrow H
\]
使得所有的\(x,z \in X\),函数\(K(x,z)\)满足
\[K(x,z) = \phi(x) \cdot \phi(z)
\]
则称\(K(x,z)\)为核函数,\(\phi(x)\)为映射函数。
再回顾一下之前的两种情形。由于最后要用SMO算法计算的式子形如
\[\begin{align}
\min_{\alpha} & \frac{1}{2} \sum_i \sum_j \alpha_i \alpha_j y^i y^j K(x^i, x^j) - \sum_i \alpha_i\\
\text{s.t. } & \sum_i \alpha_i y^i = 0\\
& \alpha_i \geq 0
\end{align}
\]
对输入数据决策,形如
\[y_{predict} = \text{sign} (\sum_{i \in SV} y^i \alpha_i K(x, x^i) + b)
\]
所以,我们并不需要明确知道\(\phi(x)\)是什么映射,只需要知道核函数就可以了。
一种很常见的核函数是高斯核函数。
\[K(x, z) = \exp(-\frac{||x-z||^2}{2\sigma^2})
\]
参考
看了这篇文章你还不懂SVM你就来打我
拉格朗日对偶性













 浙公网安备 33010602011771号
浙公网安备 33010602011771号