深度学习入门-基于Python的理论与实现(鱼书)学习笔记-Chapter7-卷积神经网络
Chapter7. 卷积神经网络
卷积神经网络(CNN)主要用于图像识别,语音识别等场合
之前的神经网络是全连接的,即相邻层的所有神经元之间都有连接,这称为全连接
卷积神经网络新增了卷积层和池化层,而没有使用全连接
我们来看一下对比
全连接网络(FNN)
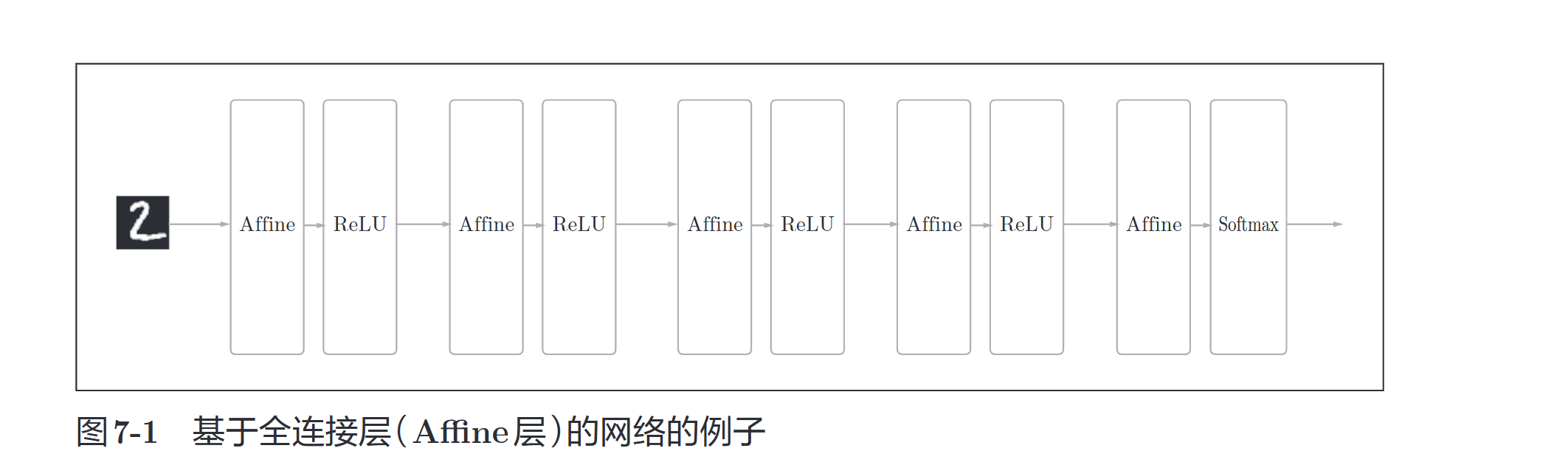
卷积神经网络(CNN)

7.1 卷积层
7.1.1 全连接层存在的问题
数据的形状被忽视了
比如输入数据是图像时,图像通常是高、长、通道方向上的3维形状,但是,向全连接层输入时,需要将3维数据拉平为1维数据
卷积层可以保持形状不变
当输入为图像时,卷积层会以3维数据的形式接收输入数据,并同样以3维数据的形式输出至下一层。因此,在CNN中,可以(有可能)正确理解图像等具有形状的数据
在CNN中,有时将卷积层的输入输出数据称为特征图,其中,卷积层的输入数据称为输入特征图,输出数据称为输出特征图
7.1.2 卷积运算
这个看图最好理解了

滤波器有时也别称为核
具体计算流程
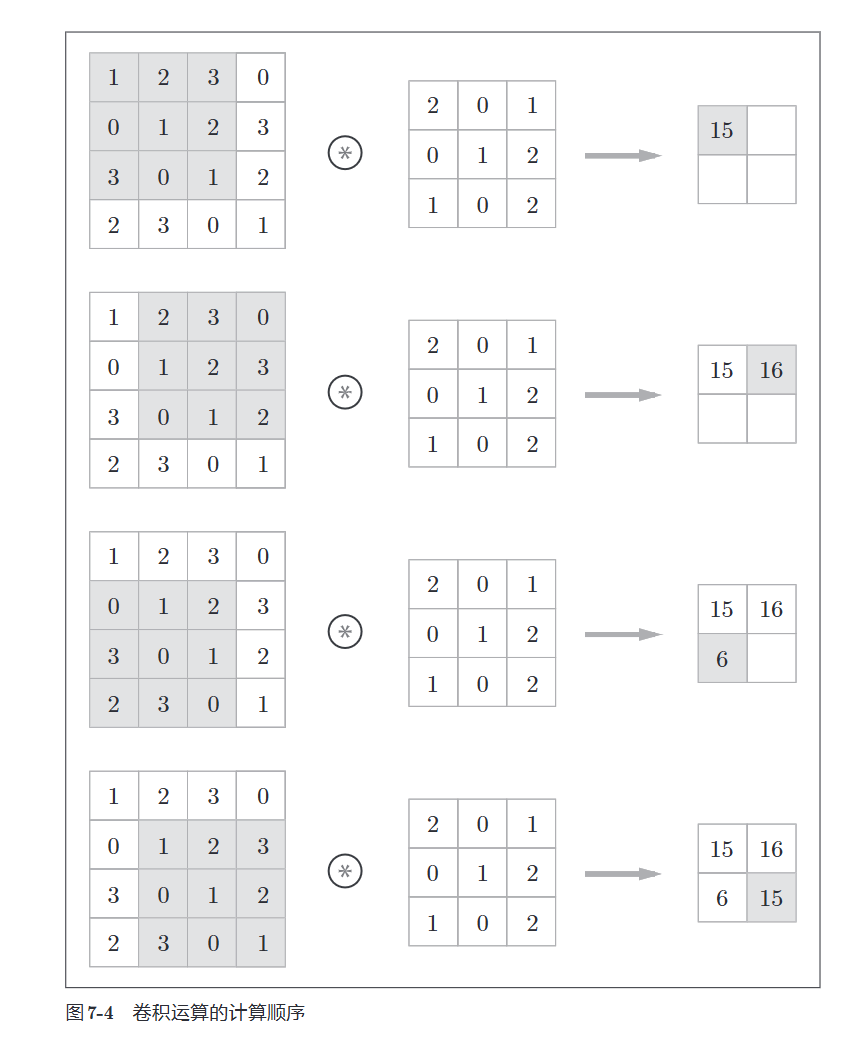
加上偏置(相当于广播运算了这里)
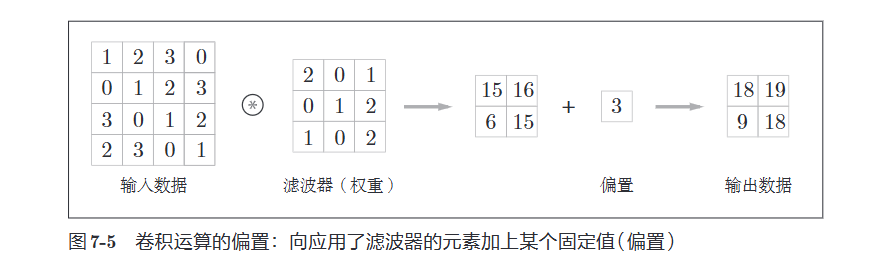
7.1.3 填充(padding)
为什么要进行填充(padding)
使用填充是为了调整输出的大小,因为使用一次卷积操作,数据就会变小一次,反复进行多次的话,那么在某个时刻输出大小可能就会变成1,导致无法再进行卷积运算,所以我们要进行填充
填充过程看图很好理解
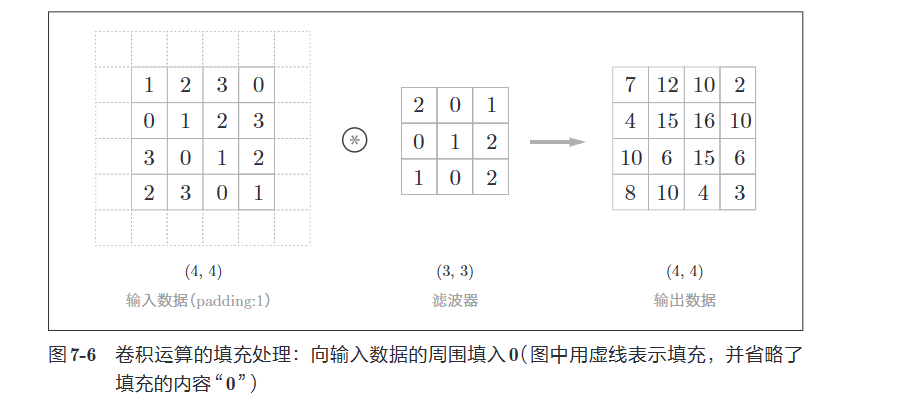
7.1.4 步幅(stride)
应用滤波器的位置间隔称为步幅(stride)
看图直接理解
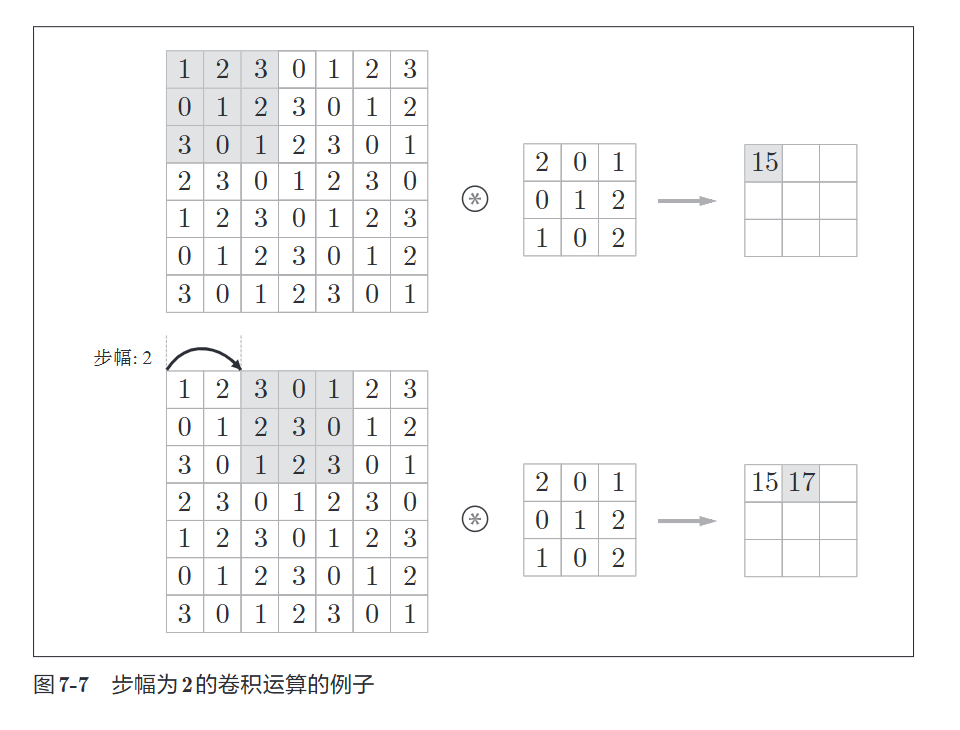
这里我们可以计算一下输出的大小
假设输入大小\((H, W)\), 滤波器大小\((FH, FW)\), 输出大小\((OH, OW)\), 填充为\(P\), 步幅为\(S\)
7.1.5 3维数据的卷积运算
与2维数据相比,纵深方向(通道方向)上的特征图增加了。通道方向上有多个特征图时,会按照通道方向进行输入数据和滤波器的卷积运算,并将结果相加得到输出
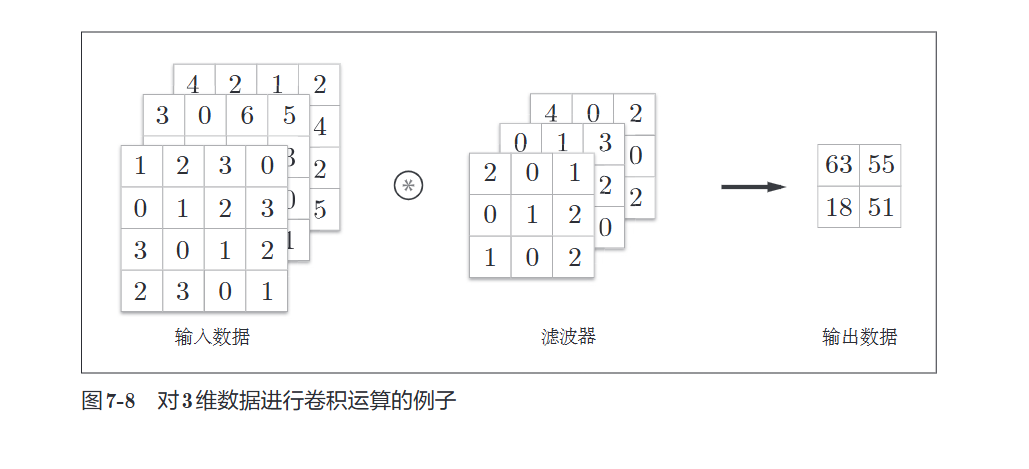
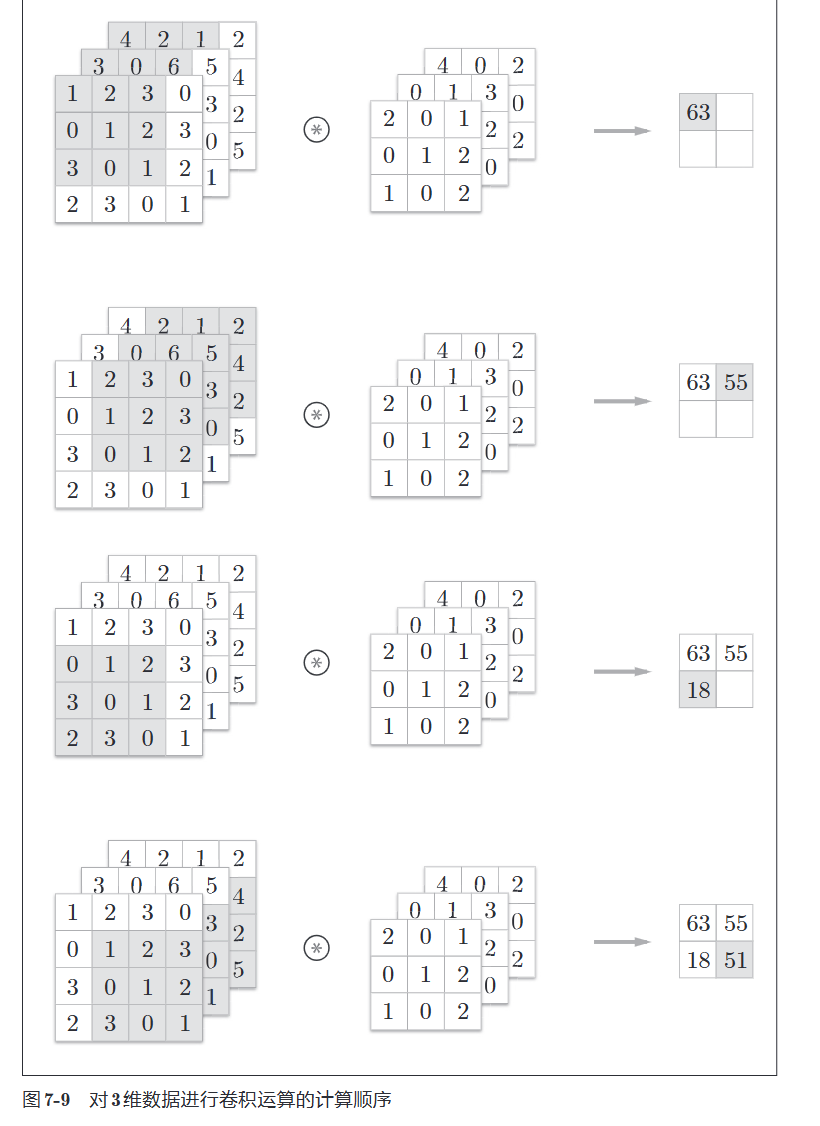
注意
在3维数据的卷积运算中,输入数据和滤波器的通道数要设为相同的值
7.1.6 结合方块思考
将数据和滤波器结合长方体的方块来考虑,3维数据的卷积运算很容易理解
这里按(通道数,高度,长度)的顺序书写
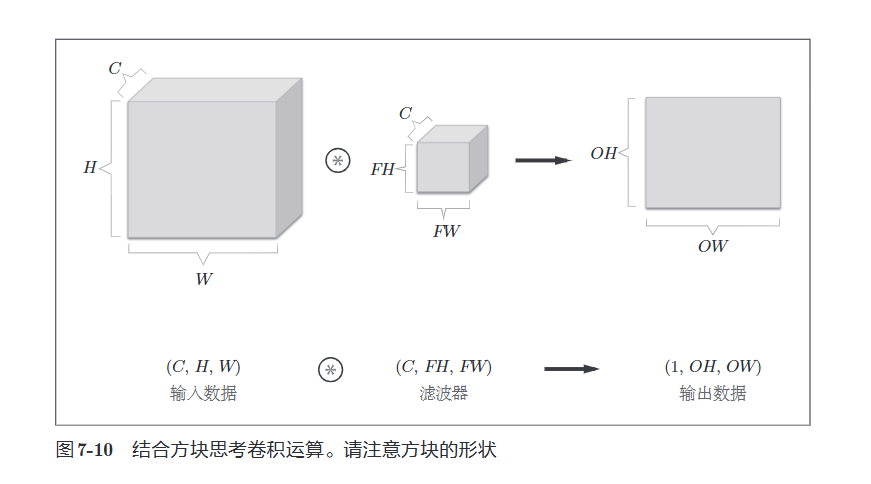
输出时1张特征图,即为通道数为1的特征图,如果要在通道方向上也拥有多个卷积运算的输出怎么做呢?
就需要多个滤波器(权重)
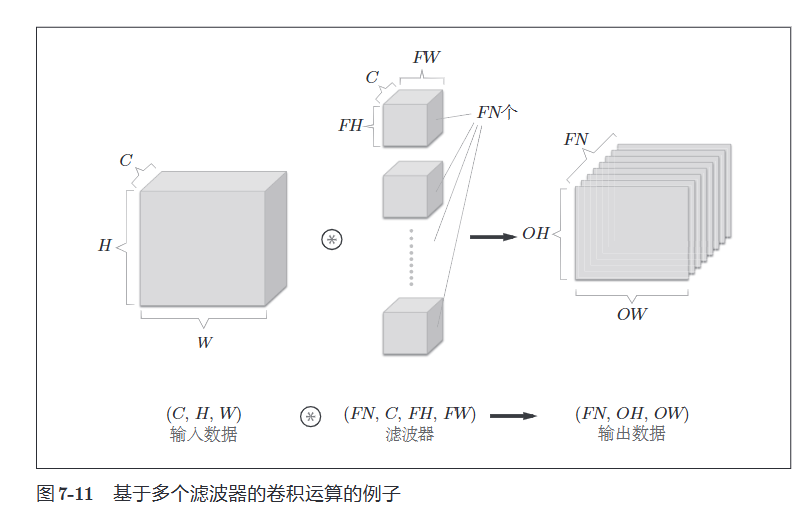
这里有一些细节还是需要注意一下
在上图中,通过应用\(FN\)个滤波器,输出特征图也生成了\(FN\)个,如果将这\(FN\)个特征图汇集在一起,就得到了形状为\((FN, OH, OW)\)的方块,将方块传给下一层,就是 \(CNN\)的处理流
关于卷积运算的滤波器,也必须考虑滤波器的数量。因此,作为\(4\)维数据,滤波器的权重数据要按(output_channel,input_channel,height,width)的顺序书写。比如,通道数为\(3\)、大小为\(5×5\)的滤波器有\(20\)个时,可以写成\((20,3,5,5)\)
卷积运算中(和全连接层一样)存在偏置,这里偏置的形状时\((FN, 1, 1)\),滤波器的输出结果的形状是\((FN,OH,OW)\)。这两个方块相加时,要对滤波器的输出结果\((FN,OH,OW)\)按通道加上相同的偏置值。另外,不同形状的方块相加时,可以基于\(NumPy\)的广播功能轻松实现
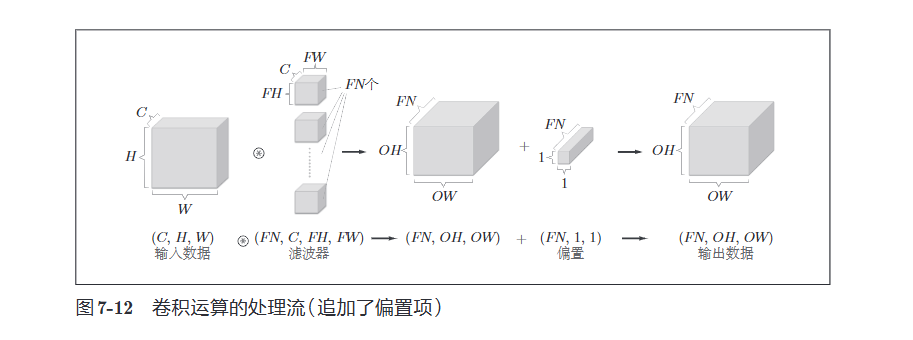
7.2.7 批处理
我们希望卷积运算也能同之前的全连接网络一样对应批处理。为此,需要将在各层间传递的数据保存为4维数据,具体地讲,就是按照(batch_num, channel, height, width)的顺序保存数据
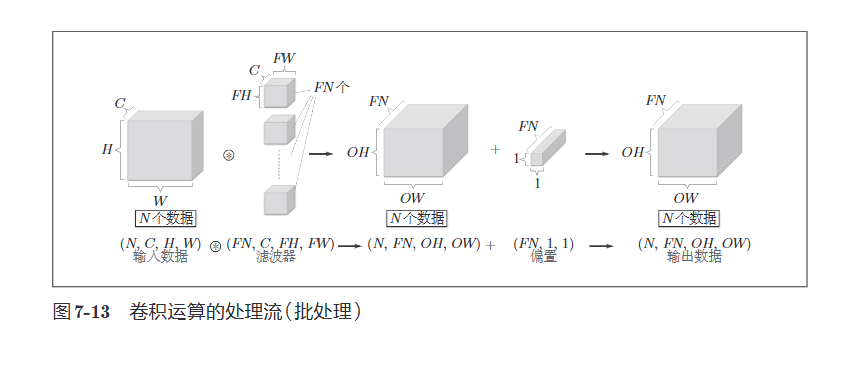
在各个数据的开头添加了批用的维度。像这样,数据作为\(4\)维的形状在各层间传递。这里需要注意的是,网络间传递的是\(4\)维数据,对这\(N\)个数据进行了卷积运算。也就是说,批处理将\(N\)次的处理汇总成了\(1\)次进行。
7.3 池化层(pooling)
池化时缩小高、长方向上的空间运算。
看图就理解了
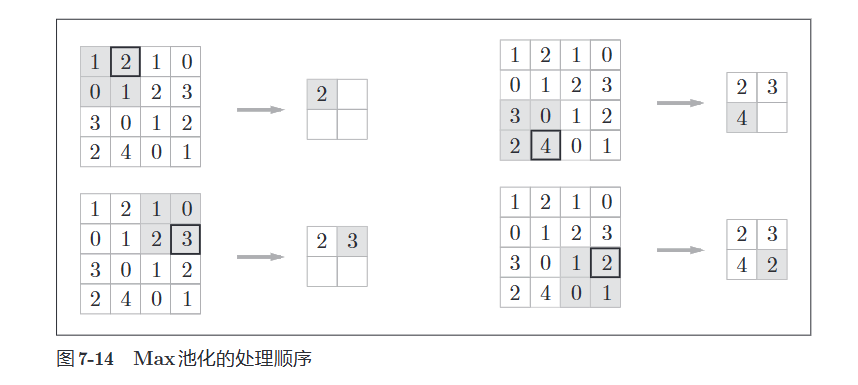
除了\(Max\), 还可以取平均等
池化层的特征
-
没有要学习的参数
实际上,池化就是一个操作,本来就不存在要学习的参数 -
通道数不发生变化
-
对微小位置变化具有鲁棒性(健壮)
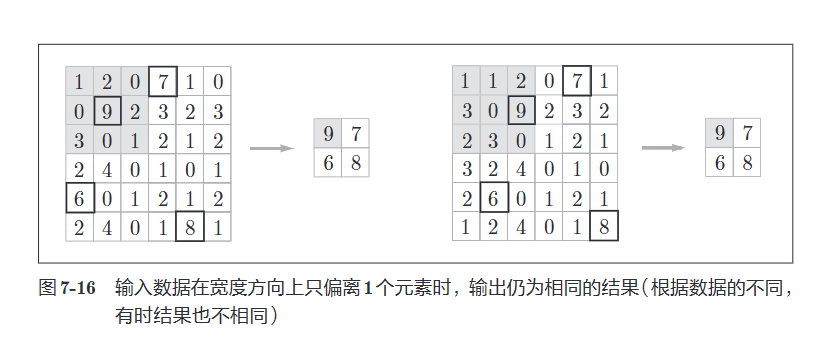
输入数据发生微小偏差时,池化仍会返回相同的结果
后话
池化的目的是缩小数据量以来减少运算成本的,所以池化的训练效果一般没有不池化的训练效果好,但是随着如今算力的越来越强大,很多模型都不再使用池化了,当算力足够的时候没有必要池化,训练效果可能还会好一些
7.4 卷积层和池化层的实现
7.4.1 基于im2col的展开
im2col 这个名称是“image to column”的缩写,翻译过来就是“从图像到矩阵”的意思。Caffe、Chainer等深度学习框架中有名为im2col的函数,并且在卷积层的实现中,都使用了im2col。
如果老老实实地实现卷积运算,估计要重复好几层for语句,这样处理会使训练变慢,这里使用im2col
传统运算
# 需要多层嵌套循环
for n in range(N): # 遍历批次
for fn in range(FN): # 遍历滤波器
for h in range(out_h): # 遍历输出高度
for w in range(out_w): # 遍历输出宽度
# 计算卷积...
im2col是一个函数,将输入数据展开以合适滤波器(权重)
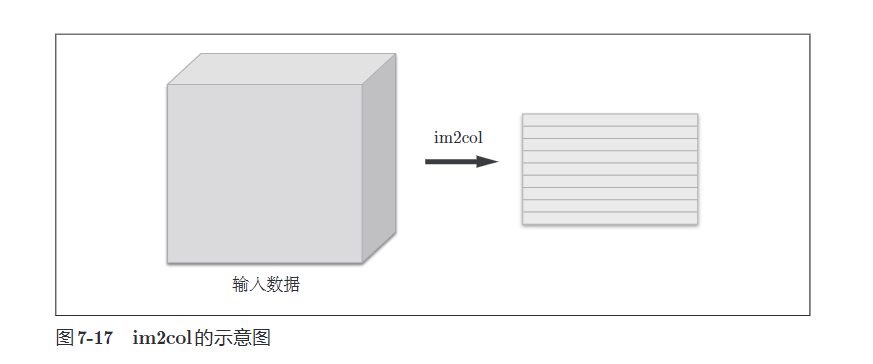
对\(3\)维的输入数据应用im2col后,数据转换为\(2\)维矩阵(准确地讲,是把包含批数量的\(4\)维数据转换成了\(2\)维数据)。
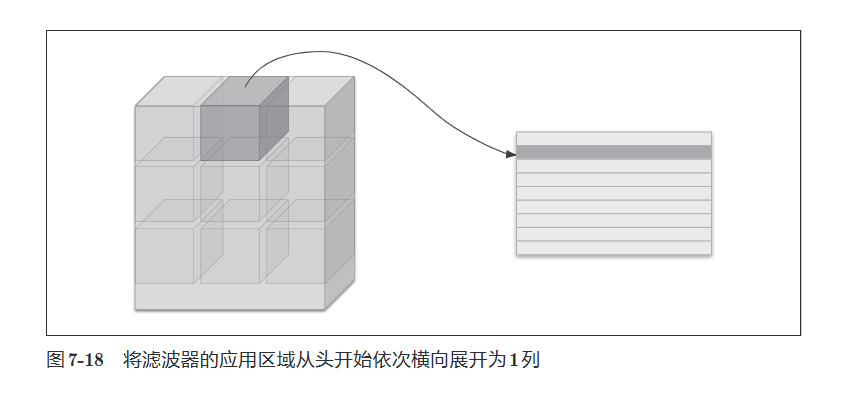
im2col会把输入数据展开以适合滤波器(权重)。具体地说,对于输入数据,将应用滤波器的区域(\(3\)维方块)横向展开为\(1\)列。im2col会在所有应用滤波器的地方进行这个展开处理。
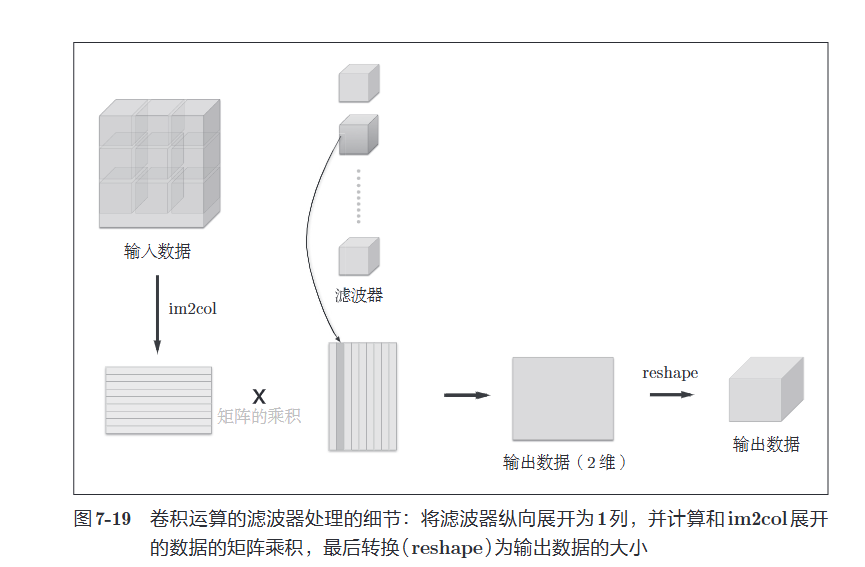
使用im2col展开输入数据后,之后就只需将卷积层的滤波器(权重)纵向展开为$$1$列,并计算\(2\)个矩阵的乘积即可。这和全连接层的Affine层进行的处理基本相同。如图7-19所示,基于im2col 方式的输出结果是\(2\)维矩阵。因为CNN中数据会保存为\(4\)维数组,所以要将\(2\)维输出数据转换为合适的形状。以上就是卷积层的实现流程。
原理理解
输入图像 (1, 1, 4, 4): 展开后 col:
[1 2 3 4] [1 2 3 │ 2 3 4 │ ...]
[5 6 7 8] [5 6 7 │ 6 7 8 │ ...]
[9 10 11 12] [9 10 11 │ 10 11 12 │ ...]
[13 14 15 16]
每列对应一个滤波器窗口
3×3滤波器,步长1 →
col.shape = (4, 9) # 4个窗口位置,每个窗口9个元素

7.4.3 卷积层的实现
im2col函数
def im2col(input_data, filter_h, filter_w, stride=1, pad=0):
"""
Parameters
----------
input_data : 由(数据量, 通道, 高, 长)的4维数组构成的输入数据
filter_h : 滤波器的高
filter_w : 滤波器的长
stride : 步幅
pad : 填充
Returns
-------
col : 2维数组
"""
N, C, H, W = input_data.shape
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant')
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
for y in range(filter_h):
y_max = y + stride*out_h
for x in range(filter_w):
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
这里来实现卷积层
class Convolution:
def __init__(self, W, b, stride = 1, pad = 0):
self.W = W
self.b = b
self.stride = stride
self.pad = pad
def forward(self, x):
FN, C, FH, FW = self.W.shape
N, C, H, W = x.shape
out_h = int(1 + (H + 2 * self.pad - FH) / self.stride)
out_w = int(1 + (W + 2 * self.pad - FW) / self.stride)
# FN: Filter Number - 滤波器数量(输出通道数)
# C: Channels - 输入通道数(RGB图像为3)
# FH: Filter Height - 滤波器高度
# FW: Filter Width - 滤波器宽度
# N: 批次大小
# C: 输入通道数
# H: 输入图像高度
# W: 输入图像宽度
col = im2col(x, FH, FW, self.stride, self.pad)
col_W = self.W.reshape(FN, -1).T
out = np.dot(col, col_W) + self.b
out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
return out
展开滤波器的部分,将各个滤波器的方块纵向展开为\(1\)列。这里通过reshape(FN,-1) 将参数指定为\(-1\),这是reshape 的一个便利的功能。通过在reshape 时指定为\(-1\),reshape 函数会自动计算\(-1\) 维度上的元素个数,以使多维数组的元素个数前后一致。比如,\((10,3,5,5)\)形状的数组的元素个数共有\(750\)个,指定reshape(10,-1) 后,就会转换成\((10,75)\)形状的数组。
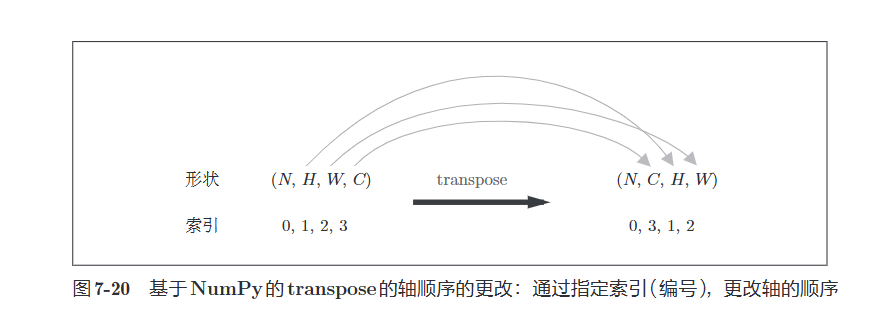
forward的实现中,最后会将输出大小转换为合适的形状。转换时使用了NumPy的transpose函数。transpose会更改多维数组的轴的顺序。如图7-20所示,通过指定从\(0\)开始的索引(编号)序列,就可以更改轴的顺序
接下来是卷积层的反向传播,注意必须进行im2col的逆处理
这里先挖个坑, 逆函数col2im先用着,稍后再学习 <\font>
def backward(self, dout):
FN, C, FH, FW = self.W.shape
dout = dout.transpose(0,2,3,1).reshape(-1, FN)
self.db = np.sum(dout, axis=0)
self.dW = np.dot(self.col.T, dout)
self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)
dcol = np.dot(dout, self.col_W.T)
dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)
return dx
7.4.4 池化层的实现
池化层的实现和卷积层相同,都使用im2col展开输入数据。不过,池化的情况下,在通道方向上是独立的,这一点和卷积层不同。具体地讲,池化的应用区域按通道单独展开。
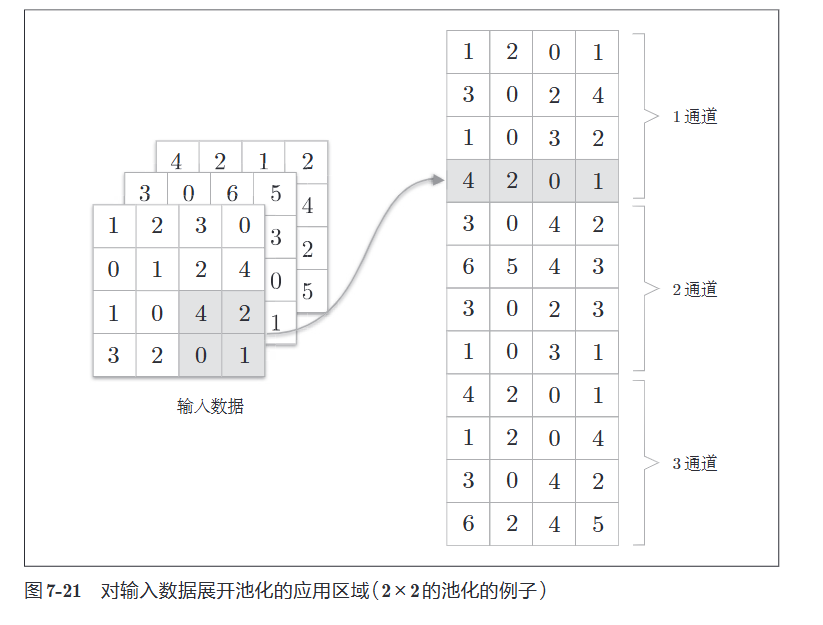
像这样展开之后,只需对展开的矩阵求各行的最大值,并转换为合适的形状即可
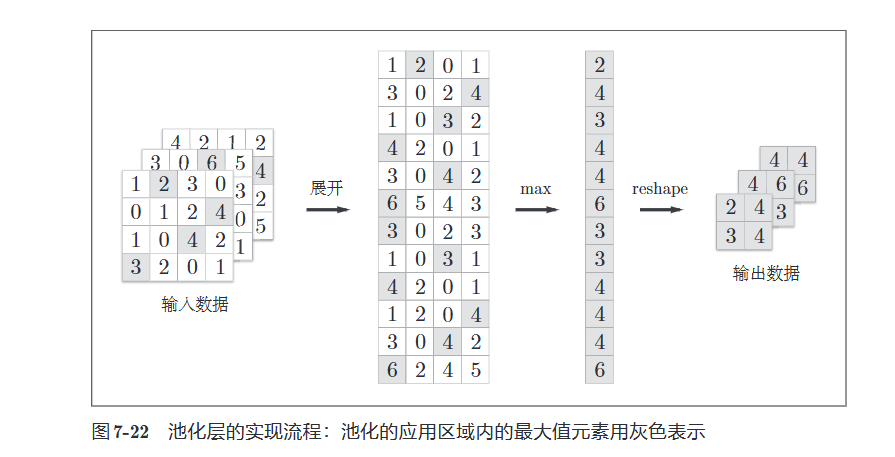
池化层的实现按下面3个阶段进行
- 展开输入数据
- 求各行的最大值
- 转换为合适的输出大小
class Pooling:
def __init__(self, pool_h, pool_w, stride = 1, pad = 0):
self.pool_h = pool_h
self.pool_w = pool_w
self.stride = stride
self.pad = pad
self.x = None
self.arg_max = None
def forward(self, x):
N, C, H, W = x.shape
out_h = int(1 + (H - self.pool_h) / self.stride)
out_w = int(1 + (W - self.pool_w) / self.stride)
col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
col = col.reshape(-1, self.pool_h * self.pool_w)
arg_max = np.argmax(col, axis = 1)
out = np.max(col, axis = 1)
out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
self.x = x
self.arg_max = arg_max
return out
def backward(self, dout):
dout = dout.transpose(0, 2, 3, 1)
pool_size = self.pool_h * self.pool_w
dmax = np.zeros((dout.size, pool_size))
dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
dmax = dmax.reshape(dout.shape + (pool_size,))
dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)
return dx
7.5 CNN的实现
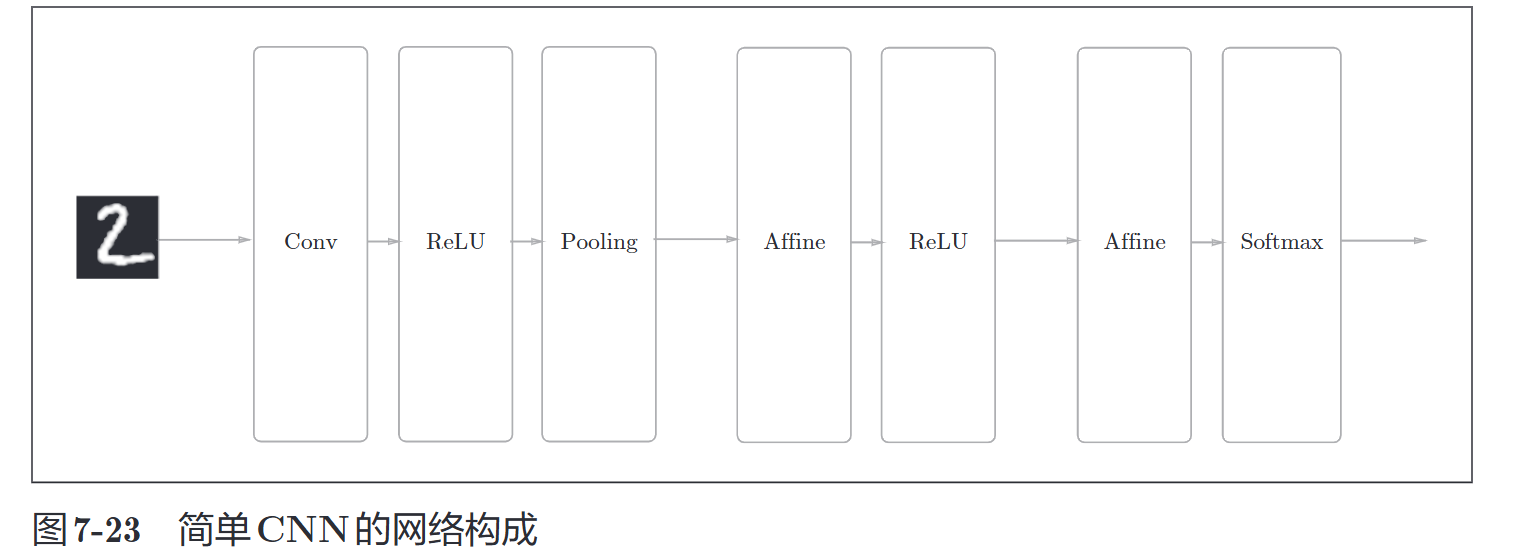
首先来看一下初始化,去下面这些参数
- input_dim : 输入数据的维度:(通道, 高, 长)
- conv_param : 卷积层的超参数(字典):
- filter_num : 滤波器的数量
- filter_size : 滤波器的大小
- stride : 步幅
- pad : 填充 - hidden_size : 隐藏层(全连接)神经元数量
- output_size : 输出层(全连接)神经元数量
- weight_int_std : 初始化时权重的标准差


 浙公网安备 33010602011771号
浙公网安备 33010602011771号