深度学习入门-基于Python的理论与实现(鱼书)学习笔记-Chapter5-误差反向传播

Chapter5 误差反向传播

5.1 计算图

通过一些问题来了解这个方法

问题1
太郎在超市买了2个100日元一个的苹果，消费税是10%，请计算支付金额

图解如下

也可以这样表示

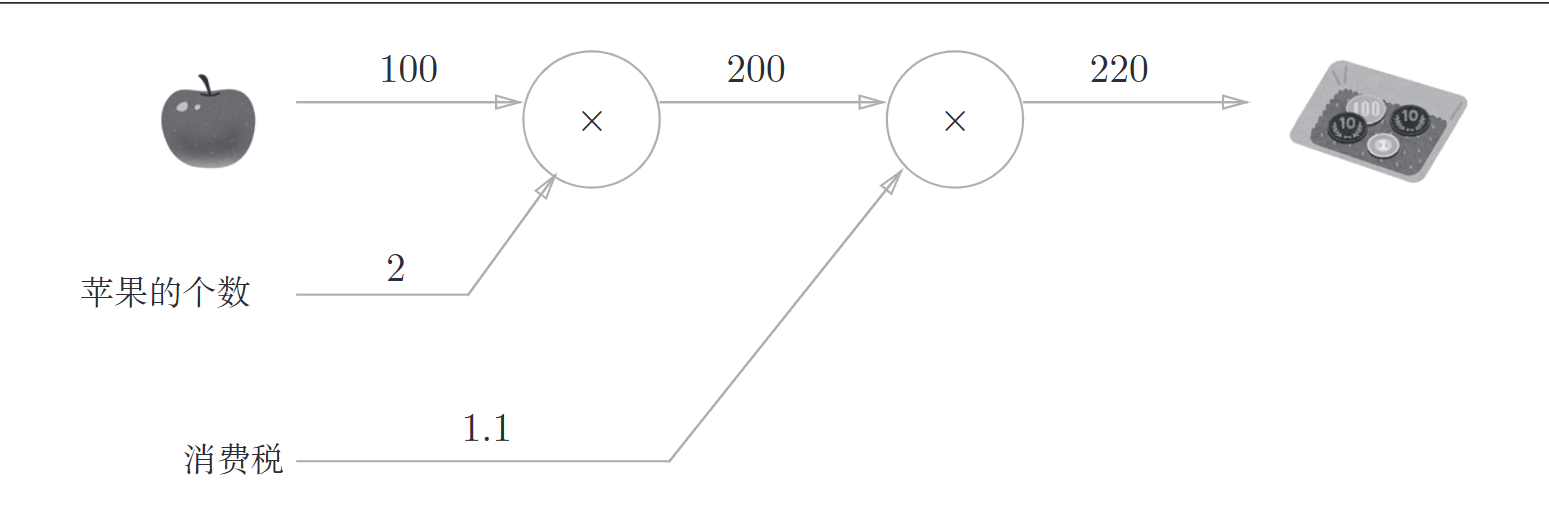
问题2
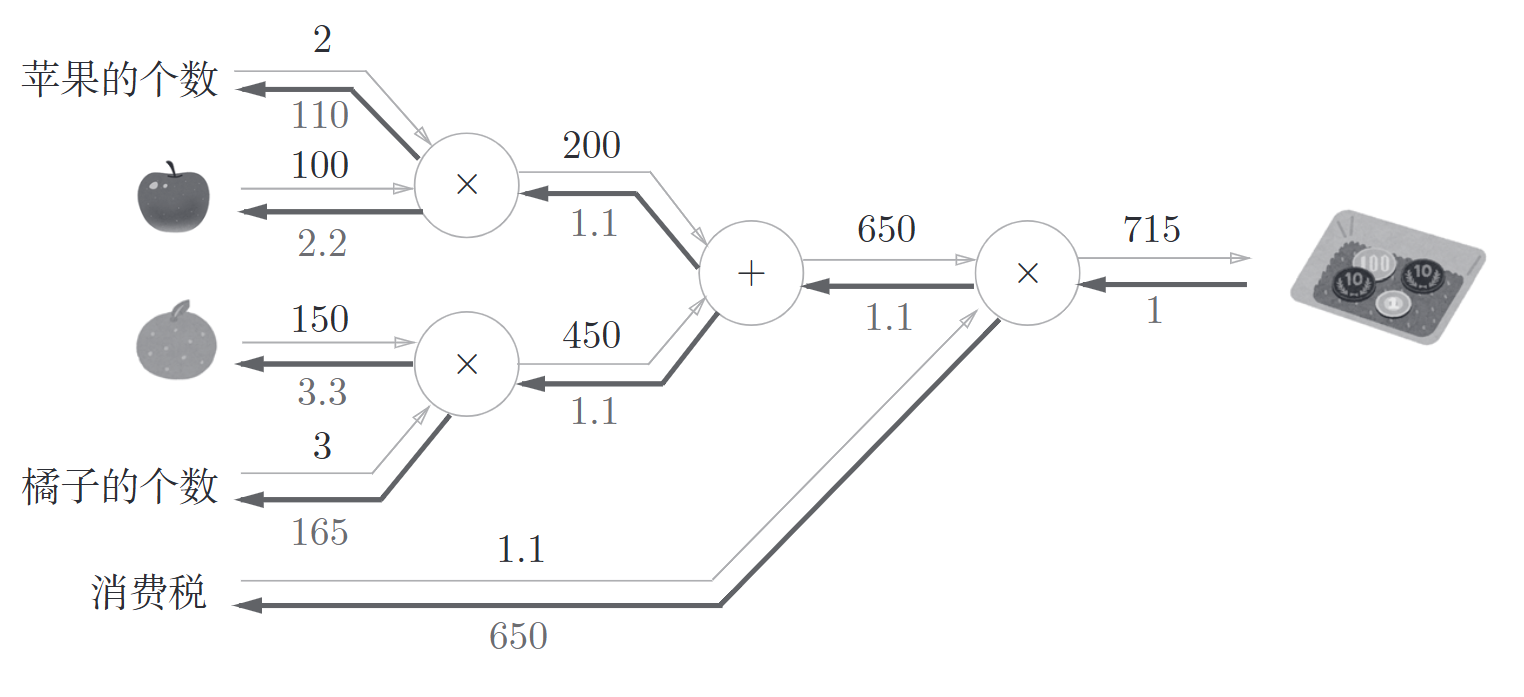
太郎在超市买了2个苹果，3个橘子。其中，苹果每个100日元，橘子每个150日元，消费税10%，请计算支付金额

图解如下

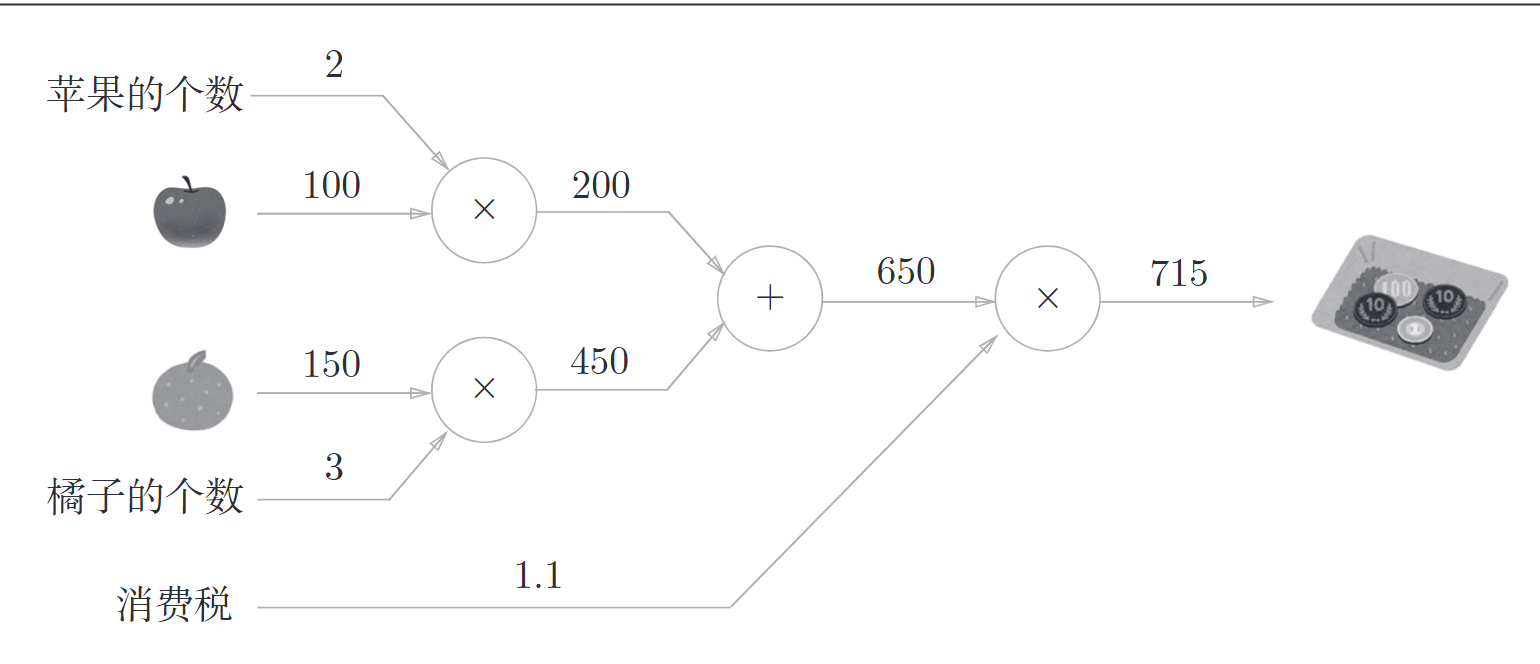
计算图按照一下流程计算：

1. 构建计算图
2. 在计算图上，从左到右进行计算(正向传播)

计算图可以通过传递局部计算获得最终结果，无论全局是多么复杂的计算，都可以通过局部计算使各个节点致力于简单的计算，从而简化问题，计算图还可以将中间的计算结果保存起来。

计算图最大的优点是可以通过反向传播高效计算导数

假设我们想知道苹果价格的上涨会多大程度上影响最终支付的金额，也就是求消费金额对苹果价格的导数，设消费金额为L，苹果价格为x, 则\(\frac{\partial L}{\partial x}\)表示当苹果价格上涨时，消费金额会上涨多少

用计算图表示

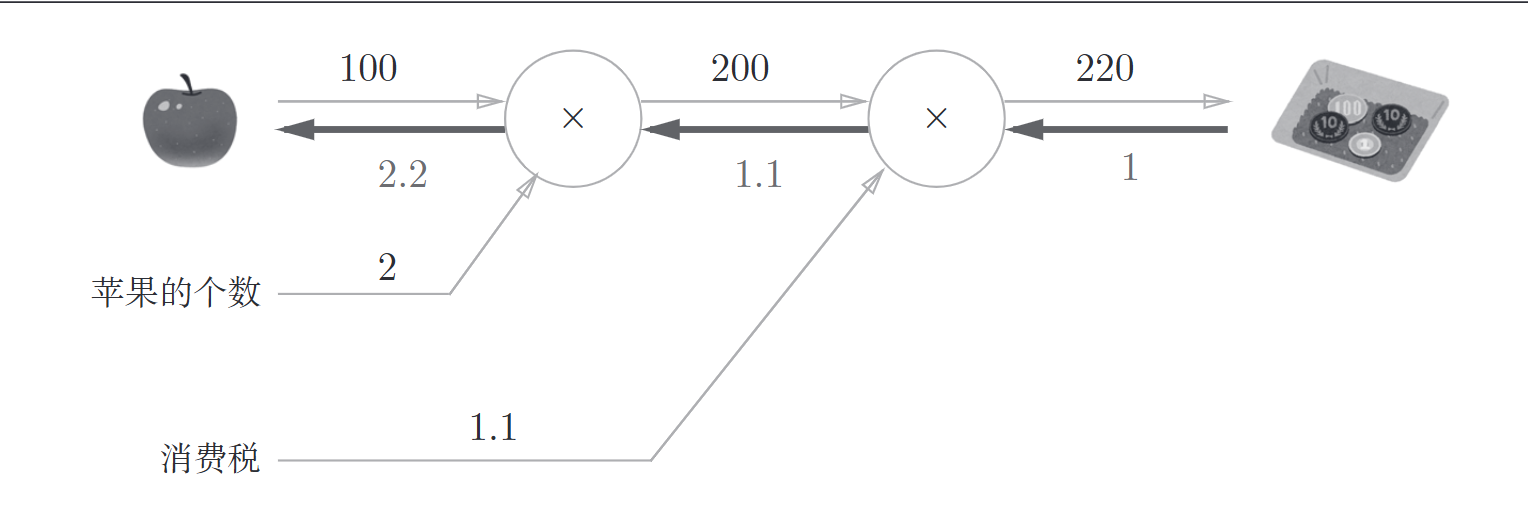
5.2 链式法则

其实就是高等数学中的内容
比如有一个函数 $$z = (x + y)^2$$
它由如下两个式子构成

\[ \begin{cases} z = t^2\\\ t = x + y \end{cases} \]

那么

\[ \frac{\partial z}{\partial x} = \frac{\partial z}{\partial t}\frac{\partial t}{\partial x} = 2t \times 1 = 2t = 2(x + y) \]

\[ \frac{\partial z}{\partial y} = \frac{\partial z}{\partial t}\frac{\partial t}{\partial y} = 2t = 2(x + y) \]

计算图表示

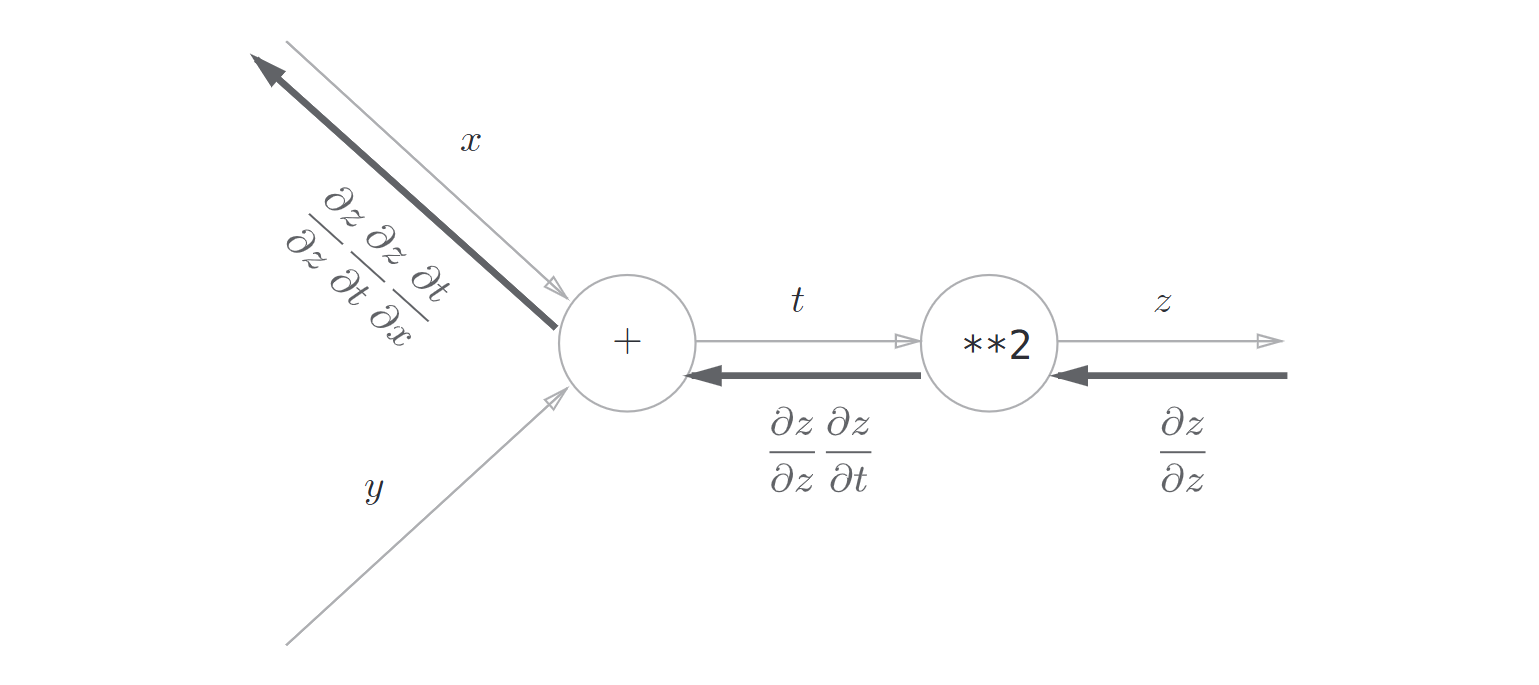
5.3 反向传播

计算图的反向传播是基于链式法则成立的，下面举两个例子

5.3.1 加法节点的反向传播

考虑函数\(z = x + y\)，那么它的导数如下

\[ \frac{\partial z}{\partial x} = 1\\\ \\\ \frac{\partial z}{\partial y} = 1 \]

也就是说从上游传过来的导数会\(\times 1\)然后流向下一个节点

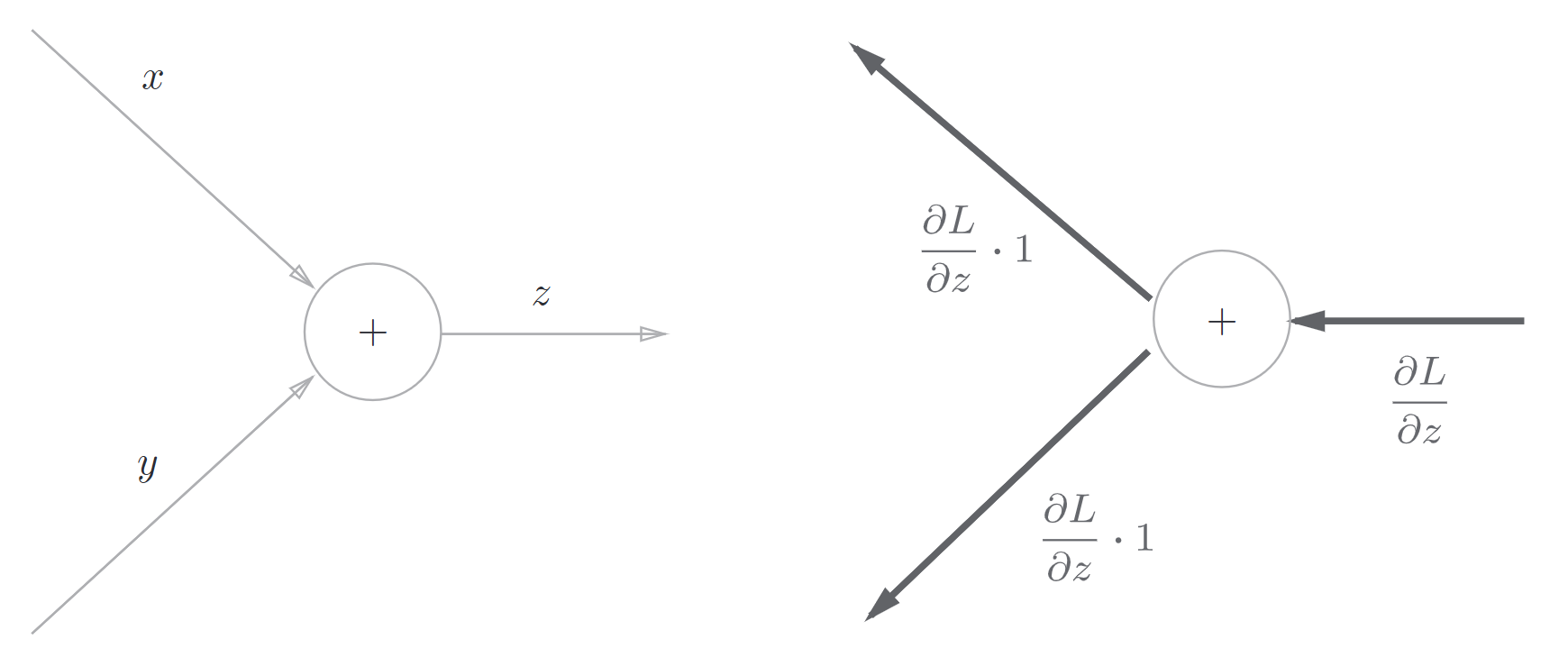
这里假设上游传过来的导数是\(\frac{\partial L}{\partial x}\)

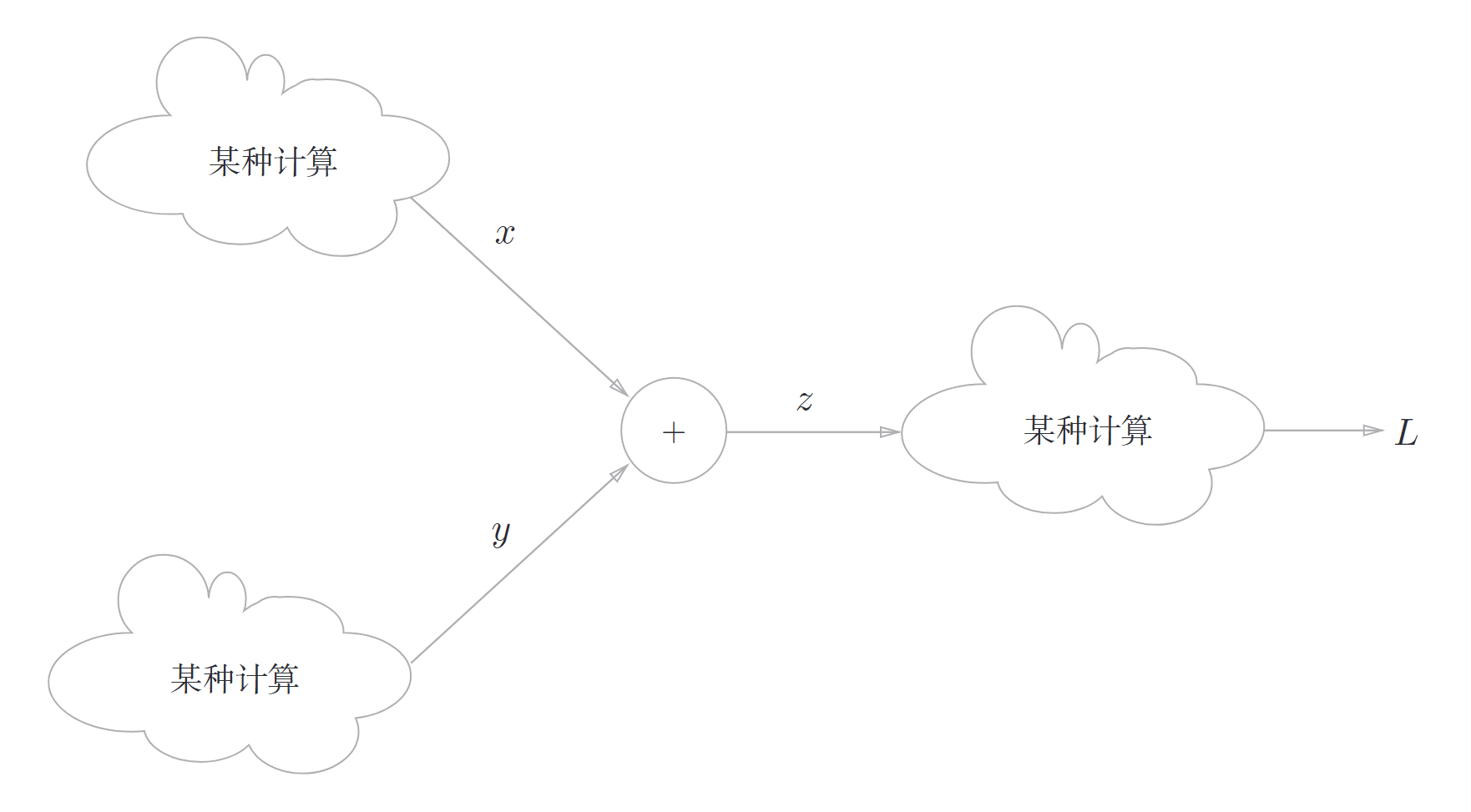
\(z = x + y\)的计算位于这个大型计算图的某个地方，从上游会传来\(\frac{\partial L}{\partial z}\)的值，并向下游传递\(\frac{\partial L}{\partial x}\) 和 \(\frac{\partial L}{\partial y}\)

5.3.2 乘法节点的反向传播

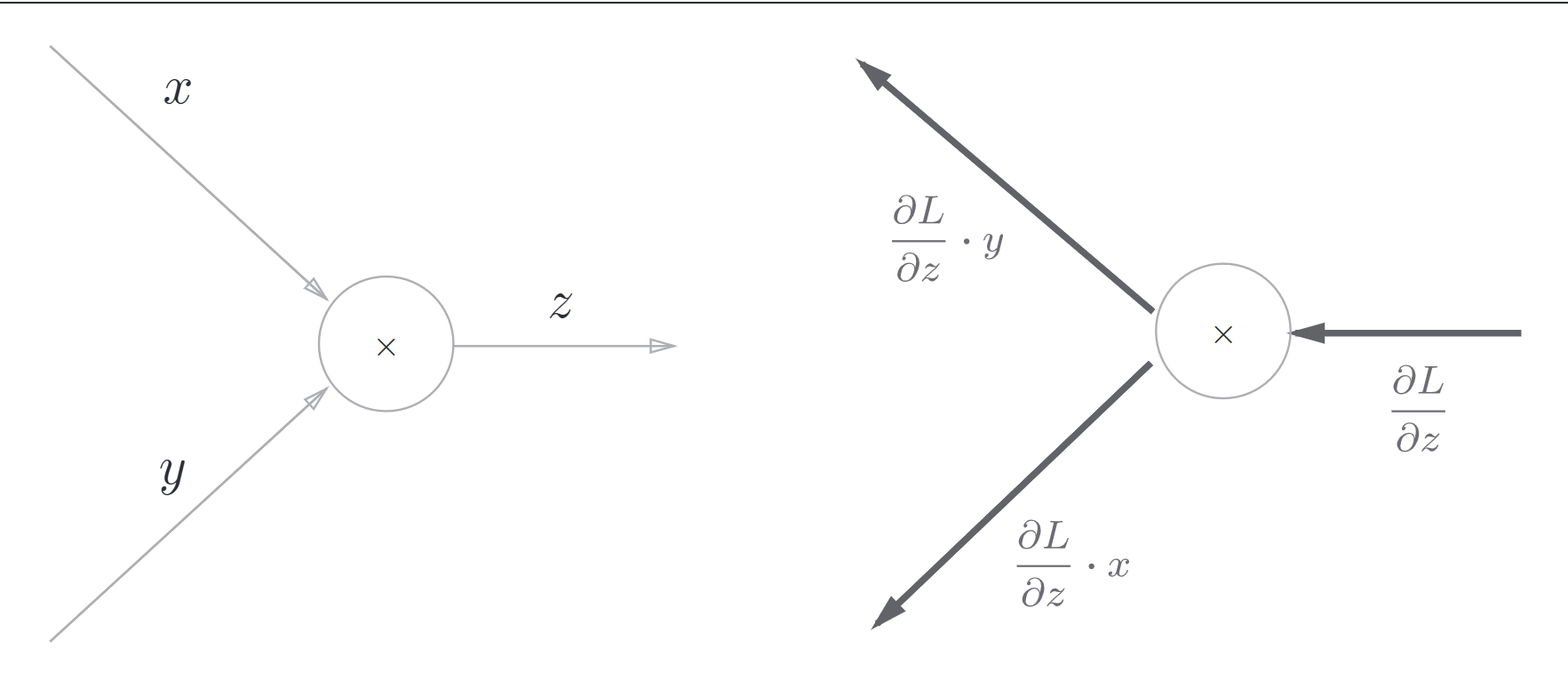
考虑函数\(z = xy\)，那么它的导数如下

\[ \frac{\partial z}{\partial x} = y\\\ \\\ \frac{\partial z}{\partial y} = x \]

原理基本类似

5.4 简单层的实现

简单实现前面买苹果的例子，这里把是实现计算图的乘法节点称为乘法层，加法节点称为加法层

5.4.1 乘法层的实现

# layer_naive.py
class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x * y

        return out
    
    def backward(self, dout):
        dx = dout * self.y
        dy = dout * self.x

        return dx, dy
    

class AddLayer:
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y

        return out
    
    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1

        return dx, dy

举个例子，计算之前的计算图

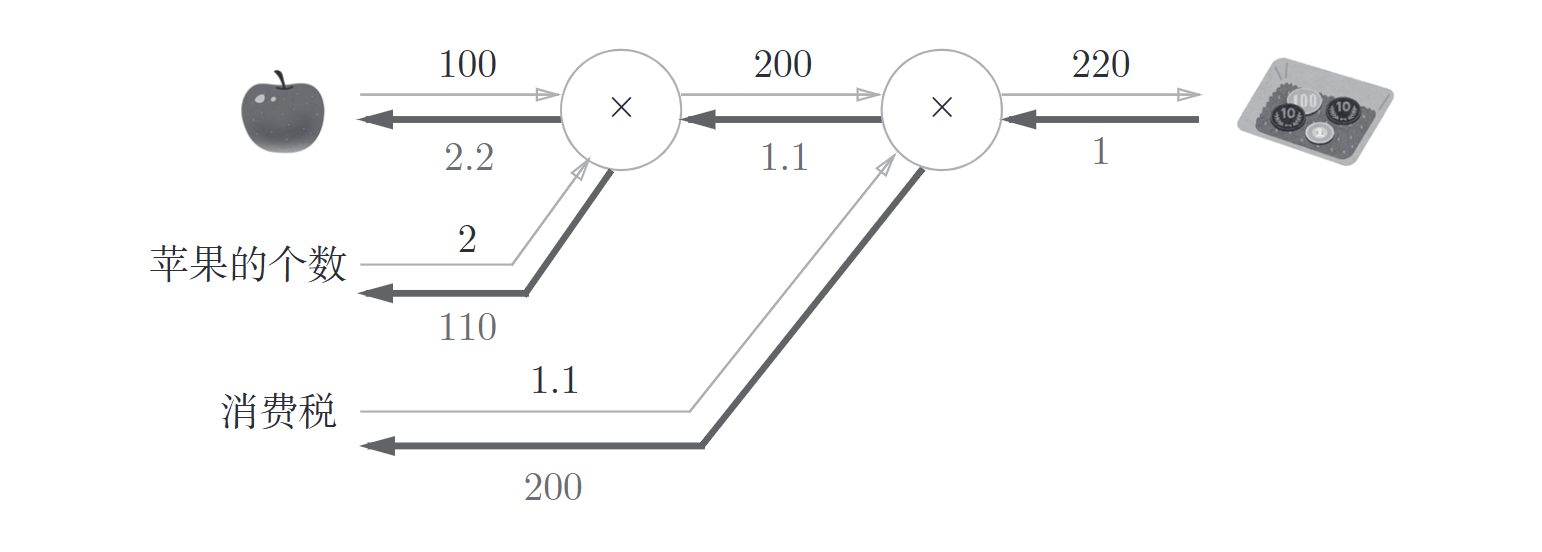
from layer_naive import *

apple = 100
apple_num = 2
tax = 1.1

mul_apple_layer = MulLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num)
price = mul_tax_layer.forward(apple_price, tax)

# backward
dprice = 1
dapple_price, dtax = mul_tax_layer.backward(dprice)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)

print("price:", int(price))
print("dapple:", dapple)
print("dapple_num:", int(dapple_num))
print("dtax:", dtax)

5.4.2 加法层的实现

class AddLayer:
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y

        return out
    
    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1

        return dx, dy

接下来实现一个购买2个苹果和3个橘子的例子

from layer_naive import *

apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1

# layer
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num)                         # (1)
orange_price = mul_orange_layer.forward(orange, orange_num)                     # (2)
all_price = add_apple_orange_layer.forward(apple_price, orange_price)           # (3)
price = mul_tax_layer(all_price, tax)                                           # (4)

# backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice)                               # (4)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)       # (3)
dorange, dorange_num = mul_orange_layer.backward(dorange_price)                 # (2)
dapple, dapple_num = mul_apple_layer.backward(dall_price)                       # (1)

计算图中层的实现(这里是加法层和乘法层)非常简单，使用这些层可以进行复杂的导数计算。下面，我们来实现神将网络中使用的层。

5.5 激活函数层的实现

5.5.1 ReLU层

激活函数ReLU为

\[ y = \begin{cases} x \ (x > 0) \\\ 0 \ (x \leq 0) \end{cases} \]

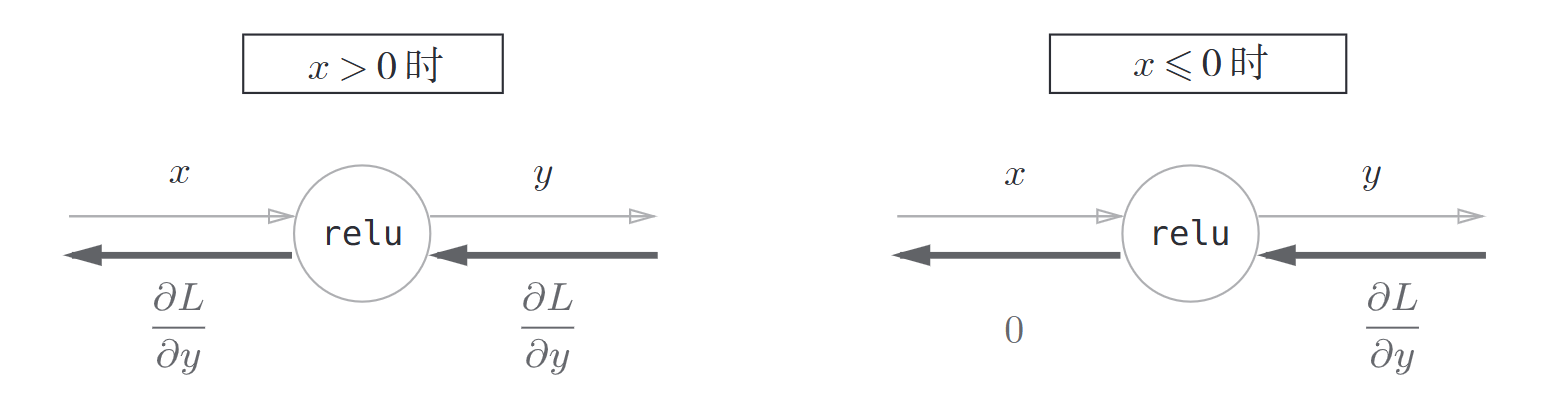
求导得到

\[ \frac{\partial y}{\partial x} = \begin{cases} 1 \ (x > 0) \\\ 0 \ (x \leq 0) \end{cases} \]

如果正向传播中输入\(x\)大于0，则反向传播会将上游的值原封不动传给下游。反之，反向传播中传给下游的信号将会停在此处

class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0

        return out
    
    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout

        return dx

mask是由True/False构成的NumPy数组,它会把正向传播时输入x的元素中小于等于0的地方保存为True，其他地方保存为False

理解
ReLU层的作用就像电路中的开关一样。正向传播时，有电流通过的话，就将开关设为ON，没有电流通过的话，就将开关设为OFF。反向传播时，开关为ON的话，电流会直接通过，否则不会有电流通过。

5.5.2 Sigmoid层

\[ y = \frac{1}{1 + e^{-x}} \]

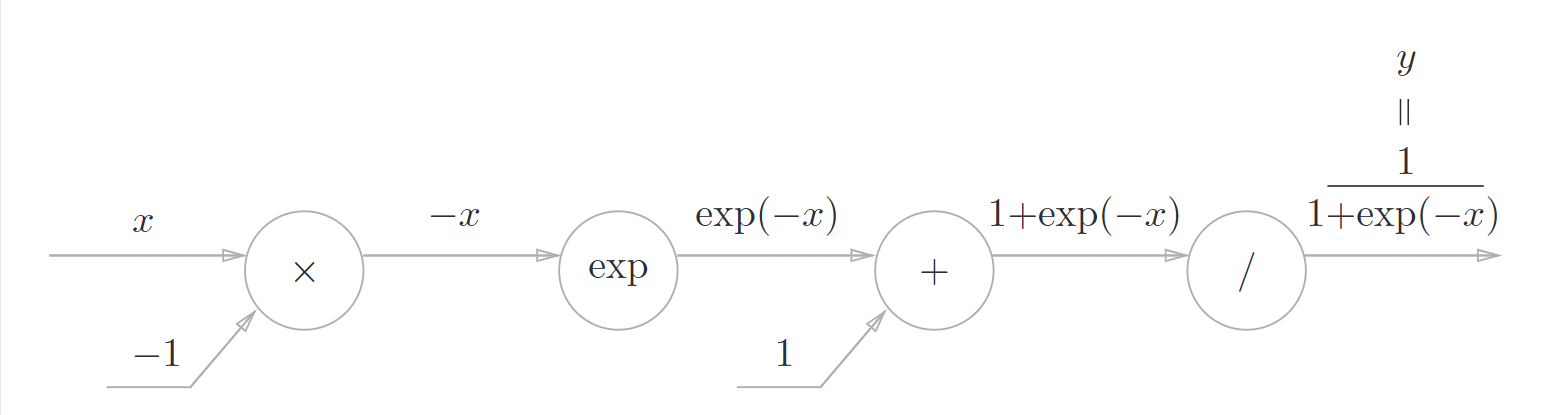
反向传播如图所示

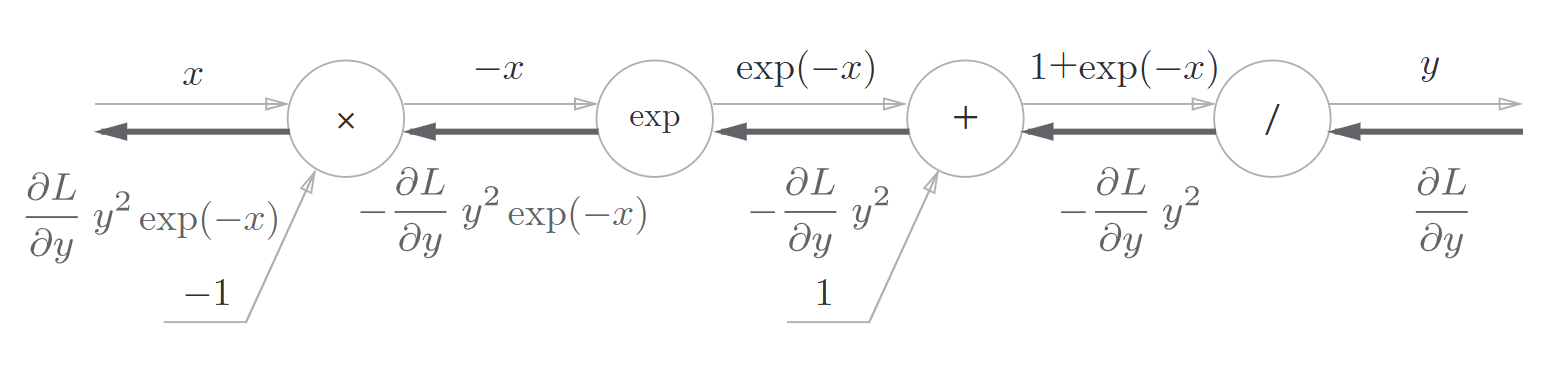
另外，可以进一步整理

\[ \frac{\partial L}{\partial y}y^2\exp(-x) = \frac{\partial L}{\partial y}y(1 - y) \]

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = sigmoid(x)
        self.out = out
        
        return out
    
    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out

        return dx

在这个实现中，正向传播时将输出保存在了实例变量out中。然后，反向传播时，使用该变量out进行计算

5.6 Affine/Softmax层的实现

神经网络的正向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”。因此，这里将进行仿射变换的处理实现为“Affine”层

Affine层的计算图

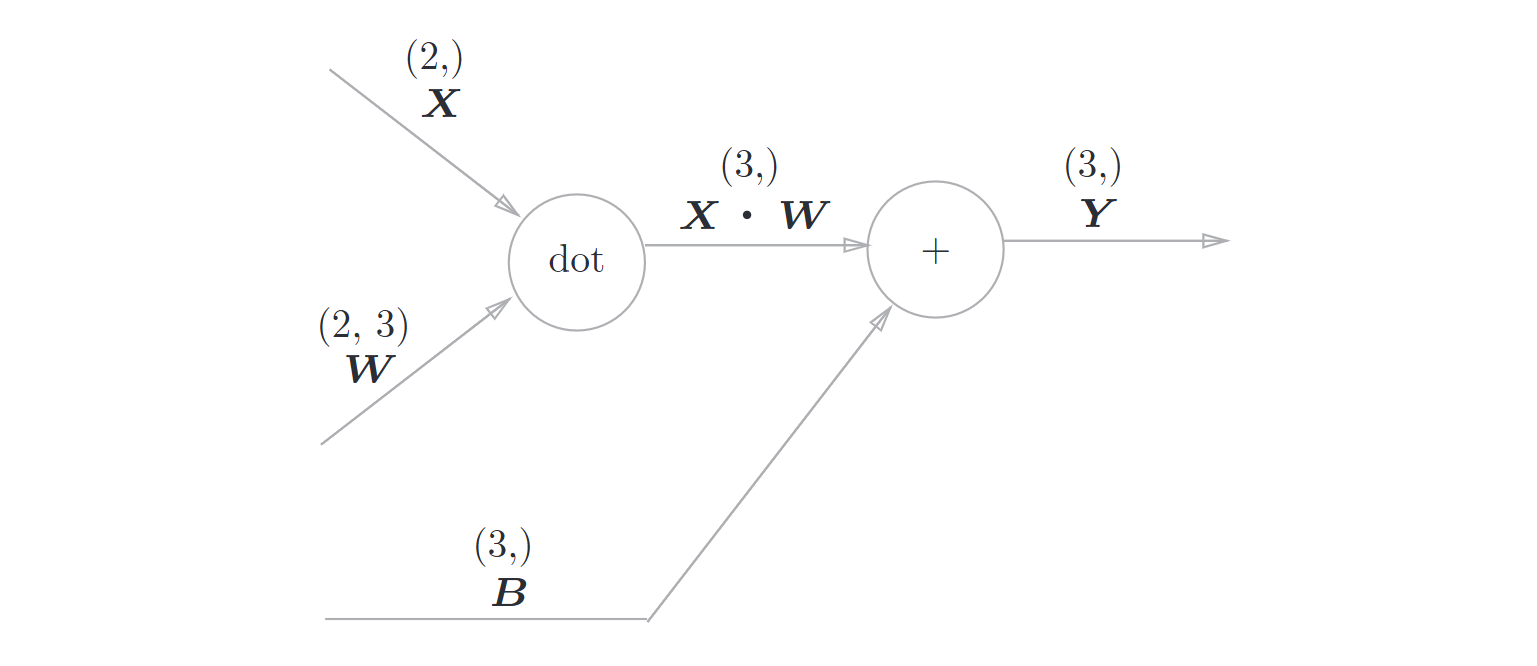
反向传播如图

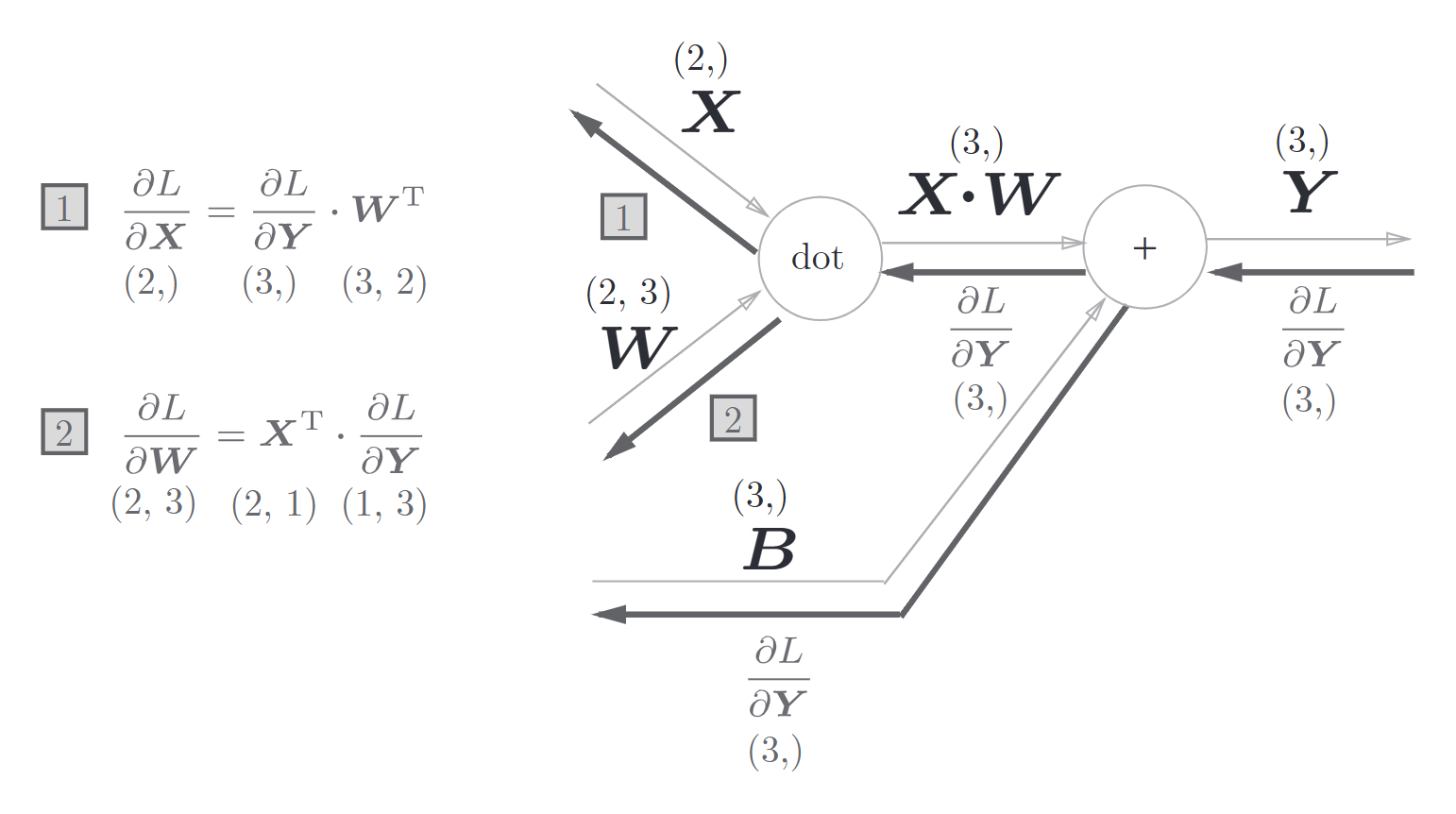
批版本的Affine层

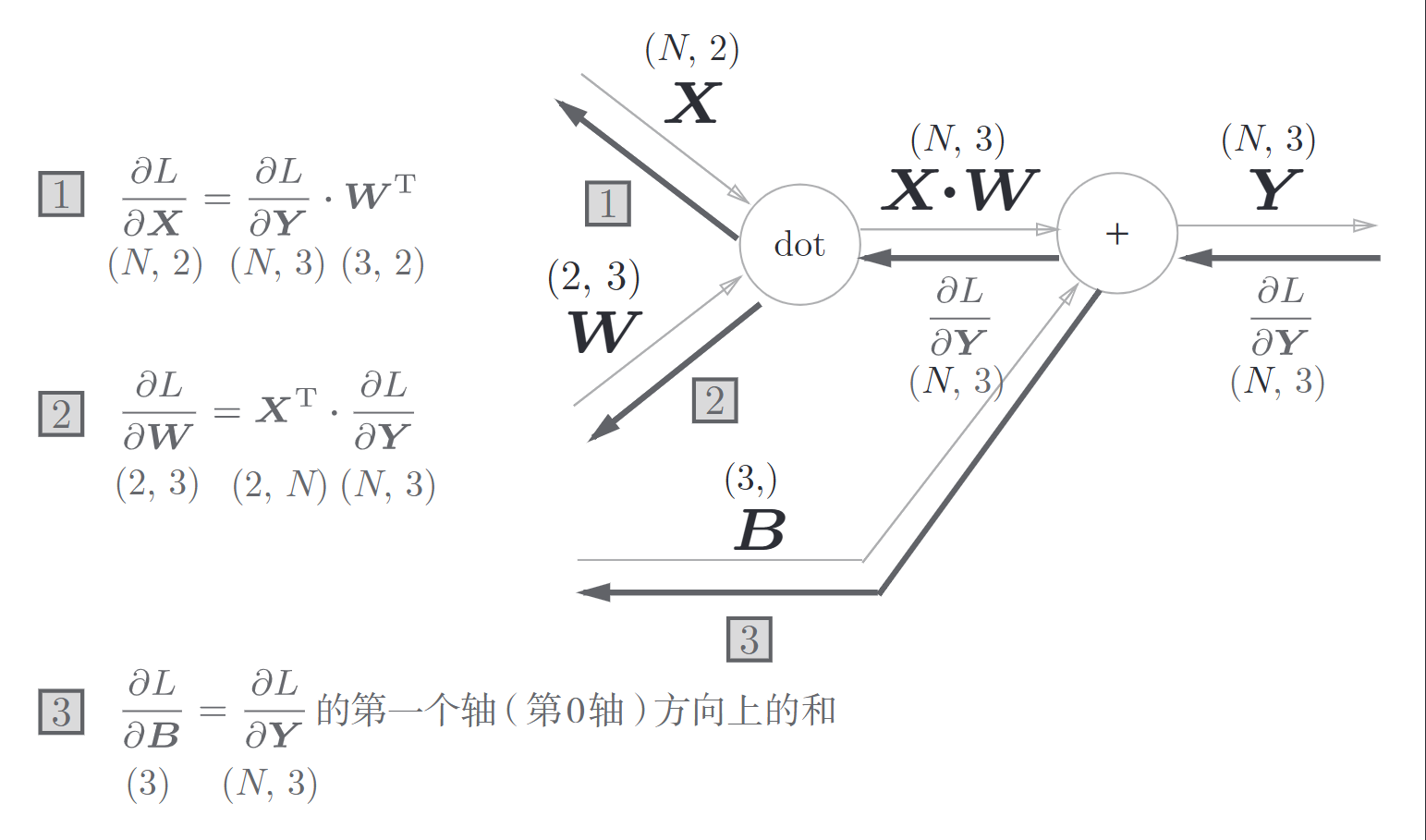
(挖个新坑，这里的矩阵微分也许还要总结一下)

加上偏置时需要特别注意的是：正向传播时，偏置被加到\(X\cdot W\)的各个数据上，这里相当于NumPY的广播。

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b

        self.x = None
        self.original_x_shape = None
        # 权重和偏置参数的导数
        self.dW = None
        self.db = None

    def forward(self, x):
        # 对应张量
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x
        out = np.dot(self.x, self.W) + self.b
        
        return out
    
    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis = 0)
        # 这里求和是因为偏置对每个样本都有影响
        dx = dx.reshape(*self.original_x_shape) #还原输入数据的形状（对应张量）
        return dx

Softmax-with-loss层

输出层的\(softmax\)函数会将输出值正规化之后再输出(这里可以理解为转化为了概率输出)

神经网络中进行的处理有推理和学习两个阶段。神经网络的推理通常不使用\(Softmax\)层。神经网络未被正规化的输出结果有时被称为“得分”。也就是说，当神经网络的推理只需要给出一个答案的情况下，因为此时只对得分最大值感兴趣，所以不需要\(Softmax\)层。不过，神经网络的学习阶段则需要\(Softmax\)层

这里来实现\(Softmax\)层，考虑到这里包含作为损失函数的交叉熵误差，所以称为\(Softmax-with-Loss\)层

计算图如下：

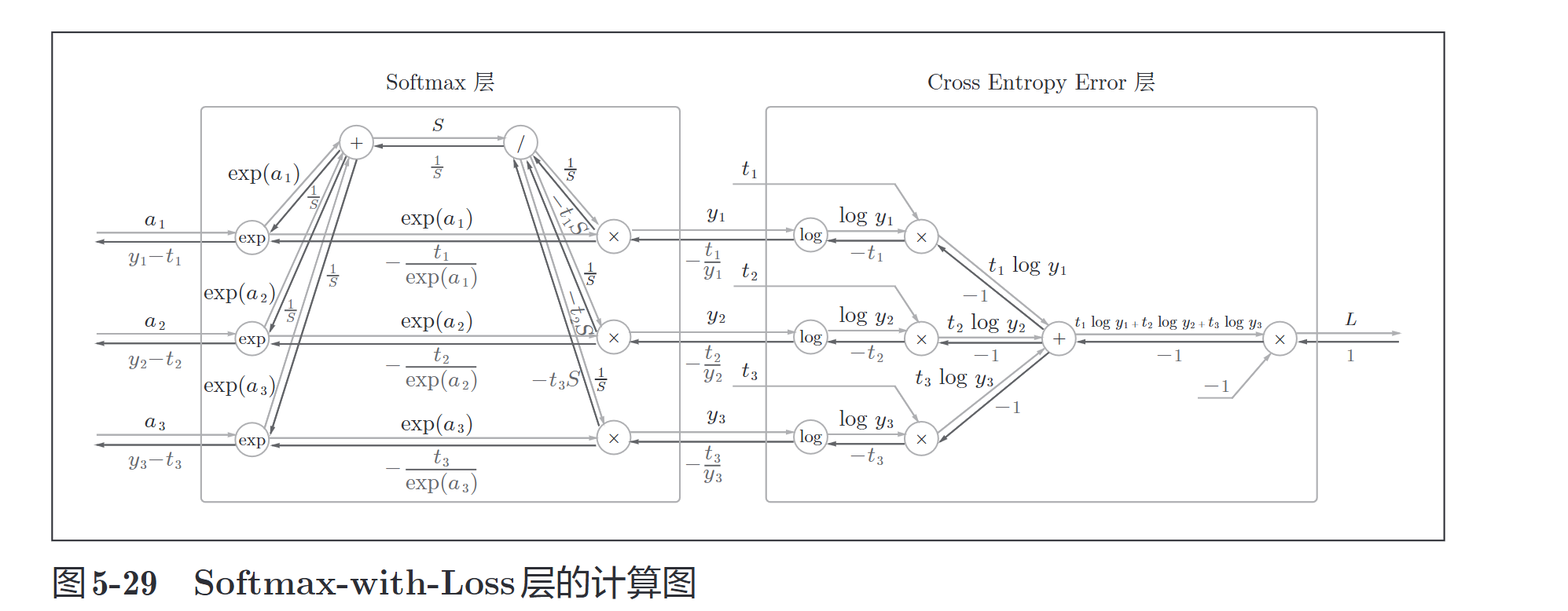
简化版

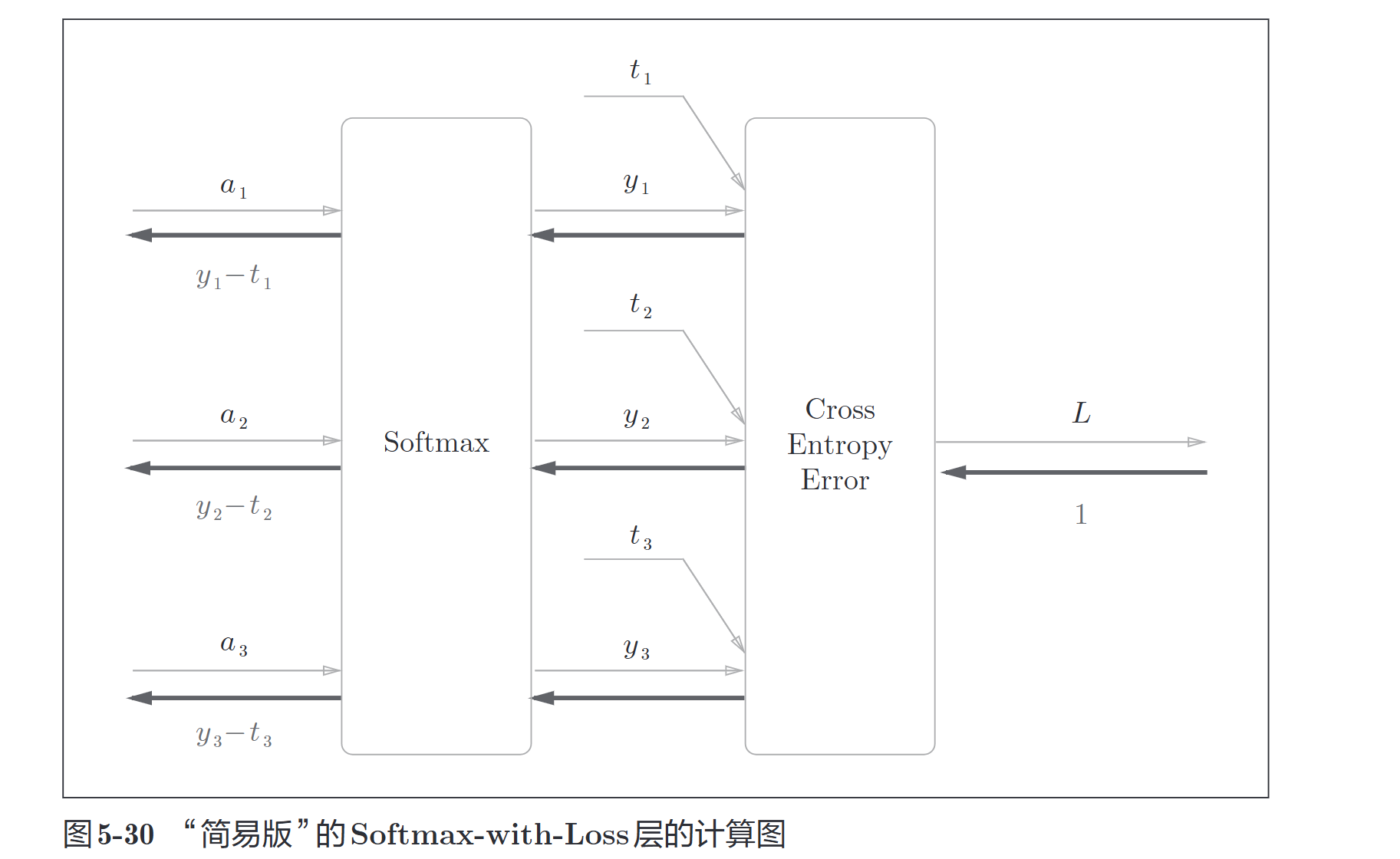
注意

使用交叉熵误差作为\(softmax\)函数的损失函数后，反向传播得到\(（y1−t1,y2−t2,y3−t3）\)这样 “漂亮”的结果。实际上，这样“漂亮”的结果并不是偶然的，而是为了得到这样的结果，特意设计了交叉熵误差函数。回归问题中输出层使用“恒等函数”，损失函数使用“平方和误差”，也是出于同样的理由。也就是说，使用“平方和误差”作为“恒等函数”的损失函数，反向传播才能得到\(（y1−t1,y2−t2,y3−t3）\)这样“漂亮”的结果。

class SoftmaxWithLoss:
    def __init___(self):
        self.loss = None
        self.y = None #softmax的输出
        self.t = None #监督数据

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        
        return self.loss
    
    def backward(self, dout = 1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size: #监督数据是ont-hot-vector的情况
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size

        return dx

5.7 误差反向传播法的实现

5.7.1 神经网络学习的全貌图

前提
神经网络中有合适的权重和偏置，调整权重和偏置以便拟合训练数据的过程称为学习。神经网络的学习分为下面4个步骤。

• 步骤1（\(mini-batch\)）
  从训练数据中随机选择一部分数据。
  
  
• 步骤2（计算梯度）
  计算损失函数关于各个权重参数的梯度。
  
  
• 步骤3（更新参数）
  将权重参数沿梯度方向进行微小的更新。
  
  
• 步骤4（重复）
  重复步骤1、步骤2、步骤3。

而误差反向传播法会在步骤2中出现

5.7.2 对应误差反向传播法的神经网络的实现

我们来建一个两层的神经网络

各种参数如下

import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.layers import *
from common.gradient import numerical_gradient
from collections import OrderedDict

class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
        # 初始化权重
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)


        # 生成层
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])

        self.lastLayer = SoftmaxWithLoss()

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
        
        return x
    
    # x:输入数据，t:监督数据
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)
    
    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis = 1)
        if t.ndim != 1 : t = np.argmax(t, axis = 1)
        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy
    
    # x:输入数据，t:监督数据
    def numerical_gradient(self, x, t):
        loss_W = lambda W : self.loss(x, t)

        grads = {}
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads
    
    def gradient(self, x, t):
        # forward
        self.loss(x, t)

        # backward
        dout = 1
        dout = self.lastLayer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 设定
        grads = {}
        grads['W1'] = self.layers['Affine1'].dW
        grads['b1'] = self.layers['Affine1'].db
        grads['W2'] = self.layers['Affine2'].dW
        grads['b2'] = self.layers['Affine2'].db

        return grads

OrderedDict是有序字典，“有序”是指它可以记住向字典里添加元素的顺序。因此，神经网络的正向传播只需按照添加元素的顺序调用各层的\(forward()\)方法就可以完成处理，而反向传播只需要按照相反的顺序调用各层即可。因为\(Affine\)层和\(ReLU\)层的内部会正确处理正向传播和反向传播，所以这里要做的事情仅仅是以正确的顺序连接各层，再按顺序（或者逆序）调用各层。

5.7.3 误差反向传播法的梯度确认（验证）

数值微分一般不会出错，但是反向传播很容易出错，为了验证我们的反向传播写得对不对，就用数值微分去进行验证，说白了就是暴力打表对拍

import sys, os
sys.path.append(os.pardir)
import numpy as np
from MNIST.mnist import load_mnist
from two_layer_net import TwoLayerNet

# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

x_batch = x_train[:3]

t_batch = t_train[:3]

grad_numerical = network.numerical_gradient(x_batch, t_batch)
grad_backprop = network.gradient(x_batch, t_batch)

# 求各个权重的绝对误差的平均值
for key in grad_numerical.keys():
    diff = np.average(np.abs(grad_backprop[key] - grad_numerical[key]))
    print(key + ":" + str(diff))

5.7.4 使用误差反向传播法的学习

import sys, os
sys.path.append(os.pardir)
import numpy as np
from MNIST.mnist import load_mnist
from two_layer_net import TwoLayerNet

# 读入数据
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

iters_num = 10000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
train_acc_list = []
test_acc_list = []

iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    
    # 梯度
    #grad = network.numerical_gradient(x_batch, t_batch)
    grad = network.gradient(x_batch, t_batch)

    # 更新
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)

    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print(train_acc, test_acc)