tarjan练习-量子芯片交易问题
量子芯片交易问题(tarjan缩点 + 拓扑排序/BFS)
题目描述
D 国有 n 个研究基地和 m 条运输通道,每条通道连接这 n 个研究基地中的两个。任意两个基地之间至多只有一条直接通道。这 m 条通道中有的为单向运输,有的为双向运输,在统计条数时双向运输也计为 1 条。
D 国地广人稀,各基地之间的科研物资价格并不一致。某一种重要的实验材料——"量子芯片",在不同基地的价格可能不同,但在同一个基地,买入价与卖出价始终相同。
年轻的科研人员小林受邀前往 D 国进行学术考察。他计划从 1 号基地出发,并最终在 n 号基地结束考察之旅。在旅途中,小林可以多次经过同一个基地,也不要求经过所有基地。为了补贴差旅费用,他打算在途中最多进行一次材料买卖:选择某个基地买入量子芯片,在之后经过的另一个基地卖出,从而赚取差价。如果全程没有差价可赚,他也可以不进行交易。
输入格式
n m
val[1] val[2] ... val[n]
x1 y1 z1
x2 y2 z2
...
xm ym zm
- 第一行:两个整数 \(n, m\),分别表示基地数量与通道数量
- 第二行:\(n\) 个正整数,表示各基地的量子芯片价格(按编号顺序)
- 接下来 m 行:每行三个整数 \(x, y, z\)
- 若 \(z = 1\),表示一条从 \(x\) 到 \(y\) 的单向通道
- 若 \(z = 2\),表示 \(x\) 与 \(y\) 之间存在一条双向通道
数据范围
- \(1 ≤ n ≤ 100000\)
- \(1 ≤ m ≤ 500000\)
- \(1 ≤ x, y ≤ n\)
- \(1 ≤ z ≤ 2\)
- \(1 ≤\) 各基地的编号$ ≤ n$
- "量子芯片"价格 \(≤ 100\)
输出格式
ans
输出一个整数,表示最多能赚取的费用。若没有合适的交易,输出 0。
样例
输入
5 5
4 3 5 6 1
1 2 1
1 4 1
2 3 2
3 5 1
4 5 2
输出
5
样例解释
原图结构:
1(4) → 2(3) ⇄ 3(5) → 5(1)
↓ ↙
4(6) ⇄⇄⇄⇄⇄⇄
可能的交易策略:
-
路径 1 → 2 → 3 → 5:
- 在基地 2 买入,价格 3
- 在基地 3 卖出,价格 5
- 利润 = 5 - 3 = 2
-
路径 1 → 4 → 5 → 4 → 5:
- 在基地 5 买入,价格 1
- 回到基地 4 卖出,价格 6
- 利润 = 6 - 1 = 5
最优策略利润为 5。
思路
我们先来考虑有向无环图的情况
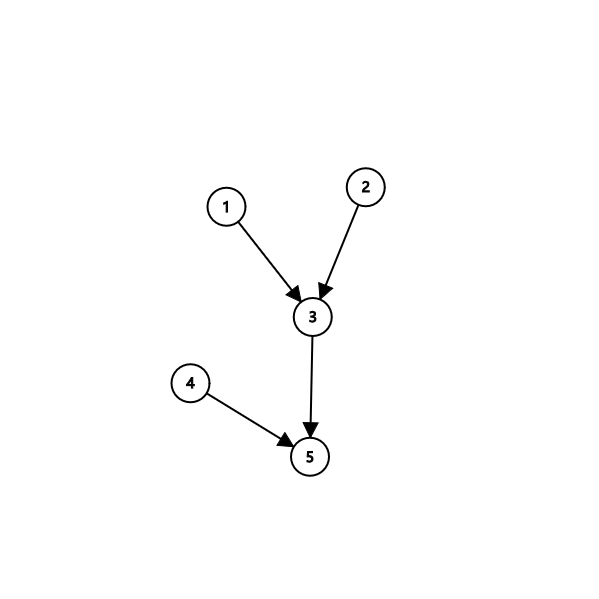
我们先来看最低买入的价钱
\(mn[1], mn[2], mn[4]\)都已经锁死不能再改变了
\(mn[4] = min(mn[4], mn[1], mn[2]), mn[5] = min(mn[4], mn[3], mn[1], mn[2])\)
可以发现最低买入的价钱是可以传递给后继节点的
然后最大收入就好算了,用自己卖出的价钱减去最低买入价钱就好了
回到本题
本题最麻烦的一点就是如果图连通的话,可以随时往回走
但是注意是图连通的情况下哦,也就是说,只能在它所在的连通分量里任意走,结合有向无环图的情况,我们可以先把它变成一个有向无环图,然后就好办了,每个连通分量的最小买入价钱就是这个连通分量的点中买入价钱最小的那一个
此外需要注意的是,有一些点既不能从1走到,也不能走到n,这些点我们需要剔除
我们可以建图的同时建一个反图,从1走一遍,从n走一遍,都走不到的点就是需要剔除的点
std::vector<int> g[maxn], rg[maxn]; // 建图和建反图
std::vector<int> SCC[maxn], dag[maxn]; // SCC[i]: i这个连通分量中有哪些点 dag[i]缩点后形成的新图
int vis1[maxn], vis2[maxn], valid[maxn], val[maxn];
int n, m, cur = 0, top = 0, cnt = 0;
int dfn[maxn], low[maxn], stk[maxn], instk[maxn], scc[maxn];
int mnprice[maxn], indeg[maxn]; // mnprice[i] i这个连通分量的最小买入价钱
const int inf = 1e14;
std::vector<int> topo;
std::queue<int> q;
Step 1. 剔除无关点
void dfs1(int u)
{
vis1[u] = 1;
for (int v : g[u])
{
if (!vis1[v]) dfs1(v);
}
}
void dfs2(int u)
{
vis2[u] = 1;
for (int v : rg[u])
{
if (!vis2[v]) dfs2(v);
}
}
dfs1(1); dfs2(n);
for(int i = 1; i <= n; i++)
{
if (vis1[i] && vis2[i]) valid[i] = 1;
}
Step 2. 缩点
void tarjan(int x)
{
dfn[x] = low[x] = ++cur;
stk[++top] = x; instk[x] = 1;
for (int v : g[x])
{
if (!dfn[v])
{
tarjan(v);
low[x] = std::min(low[x], low[v]);
}
else if (instk[v])
{
low[x] = std::min(dfn[v], low[x]);
}
}
if (dfn[x] == low[x])
{
int y; cnt++;
while(true)
{
if (y == x) break;
y = stk[top--];
instk[y] = 0;
scc[y] = cnt;
SCC[cnt].push_back(y);
}
}
}
for (int i = 1; i <= n; i++)
{
if (!dfn[i]) tarjan(i);
}
Step 3. 构建新图并拓扑排序
for (int i = 1; i <= cnt; i++) mnprice[i] = inf;
for (int i = 1; i <= cnt; i++)
{
for (int u : SCC[i])
{
mnprice[i] = std::min(mnprice[i], val[u]);
}
}
for (int u = 1; u <= n; u++)
{
if (!valid[u]) continue;
for (int v : g[u])
{
if (!valid[v]) continue;
int su = scc[u], sv = scc[v];
if (su != sv)
{
dag[su].push_back(sv);
indeg[sv]++;
}
}
}
for (int i = 1; i <= cnt; i++)
{
if (indeg[i] == 0) q.push(i);
}
while(!q.empty())
{
int u = q.front(); q.pop();
topo.push_back(u);
for (int v : dag[u])
{
mnprice[v] = std::min(mnprice[v], mnprice[u]);
indeg[v]--;
if (indeg[v] == 0) q.push(v);
}
}
Step 4. 计算并输出答案
int ans = 0;
for (int i = 1; i <= n; i++)
{
if (!valid[i]) continue;
ans = std::max(ans, std::max(0ll, val[i]) - mnprice[scc[i]]);
}
std::cout << ans << endl;
代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
const int maxn = 1e5 + 5;
const int maxm = 5e5 + 5;
std::vector<int> g[maxn], rg[maxn];
std::vector<int> SCC[maxn], dag[maxn];
int vis1[maxn], vis2[maxn], valid[maxn], val[maxn];
int n, m, cur = 0, top = 0, cnt = 0;
int dfn[maxn], low[maxn], stk[maxn], instk[maxn], scc[maxn];
int mnprice[maxn], indeg[maxn];
const int inf = 1e14;
std::vector<int> topo;
std::queue<int> q;
void dfs1(int u)
{
vis1[u] = 1;
for (int v : g[u])
{
if (!vis1[v]) dfs1(v);
}
}
void dfs2(int u)
{
vis2[u] = 1;
for (int v : rg[u])
{
if (!vis2[v]) dfs2(v);
}
}
void tarjan(int x)
{
dfn[x] = low[x] = ++cur;
stk[++top] = x; instk[x] = 1;
for (int v : g[x])
{
if (!dfn[v])
{
tarjan(v);
low[x] = std::min(low[x], low[v]);
}
else if (instk[v])
{
low[x] = std::min(dfn[v], low[x]);
}
}
if (dfn[x] == low[x])
{
int y; cnt++;
while(true)
{
if (y == x) break;
y = stk[top--];
instk[y] = 0;
scc[y] = cnt;
SCC[cnt].push_back(y);
}
}
}
void solve()
{
std::cin >> n >> m;
for (int i = 1; i <= n; i++) std::cin >> val[i];
for (int i = 1; i <= m; i++)
{
int x, y, z; std::cin >> x >> y >> z;
g[x].push_back(y);
rg[y].push_back(x);
if (z == 2)
{
g[y].push_back(x);
rg[x].push_back(y);
}
}
dfs1(1); dfs2(n);
for(int i = 1; i <= n; i++)
{
if (vis1[i] && vis2[i]) valid[i] = 1;
}
for (int i = 1; i <= n; i++)
{
if (!dfn[i]) tarjan(i);
}
for (int i = 1; i <= cnt; i++) mnprice[i] = inf;
for (int i = 1; i <= cnt; i++)
{
for (int u : SCC[i])
{
mnprice[i] = std::min(mnprice[i], val[u]);
}
}
for (int u = 1; u <= n; u++)
{
if (!valid[u]) continue;
for (int v : g[u])
{
if (!valid[v]) continue;
int su = scc[u], sv = scc[v];
if (su != sv)
{
dag[su].push_back(sv);
indeg[sv]++;
}
}
}
for (int i = 1; i <= cnt; i++)
{
if (indeg[i] == 0) q.push(i);
}
while(!q.empty())
{
int u = q.front(); q.pop();
topo.push_back(u);
for (int v : dag[u])
{
mnprice[v] = std::min(mnprice[v], mnprice[u]);
indeg[v]--;
if (indeg[v] == 0) q.push(v);
}
}
int ans = 0;
for (int i = 1; i <= n; i++)
{
if (!valid[i]) continue;
ans = std::max(ans, std::max(0ll, val[i]) - mnprice[scc[i]]);
}
std::cout << ans << endl;
}
signed main()
{
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr); std::cout.tie(nullptr);
int _t = 1;
while (_t--) solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号