三分(两种写法)

三分搜索(单峰函数求极值)

算法原理

三分法一般用来求单峰（谷）函数的极值，这里以单峰函数为例，是二分法的拓展

它可以每次将搜索区间划分为三个部分，根据目标函数值的情况丢弃一部分区间

算法步骤

1. 将区间划分为等长的三个区间 分别为\([l, midl], [midl, midr], mid[midr, r]\)

2. 无非只有这样三种情况

   • \(f(midl) > f(midr)\)
     
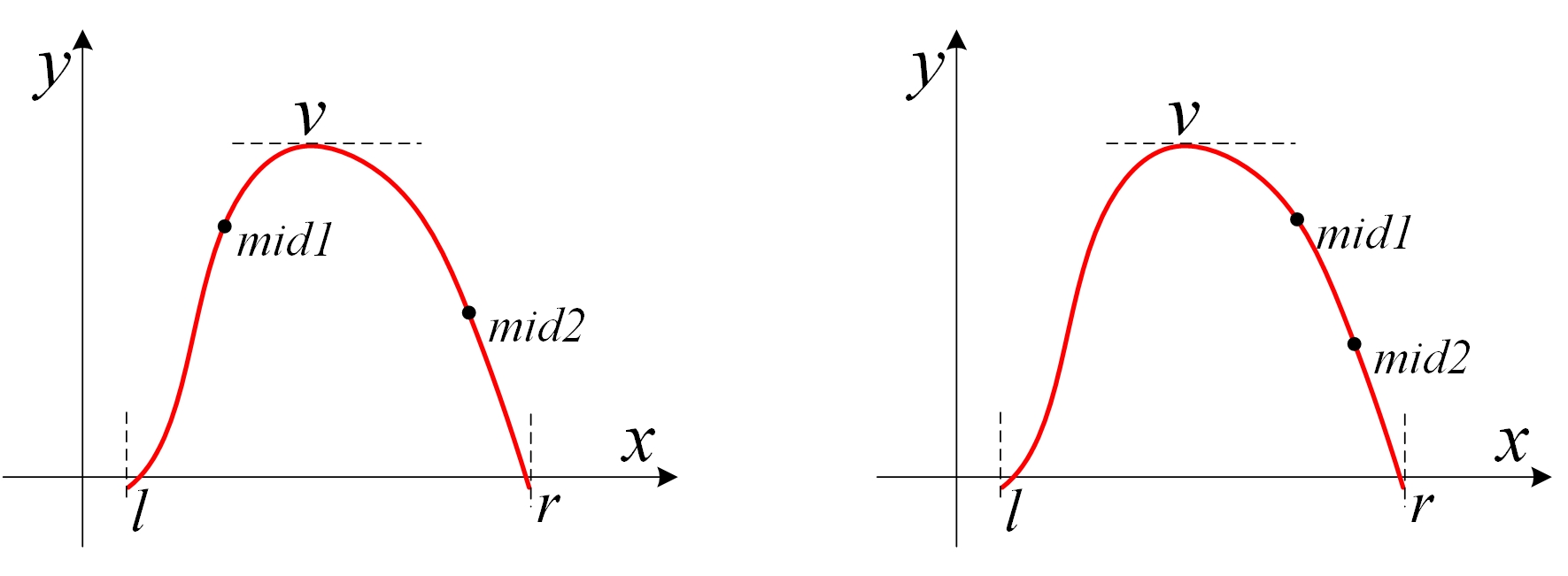
     这个时候就可以丢掉\(midr\)右边的区间了，——— 令 \(r = midr\)，然后继续分成三段

   • \(f(midl) < f(midr)\)
     
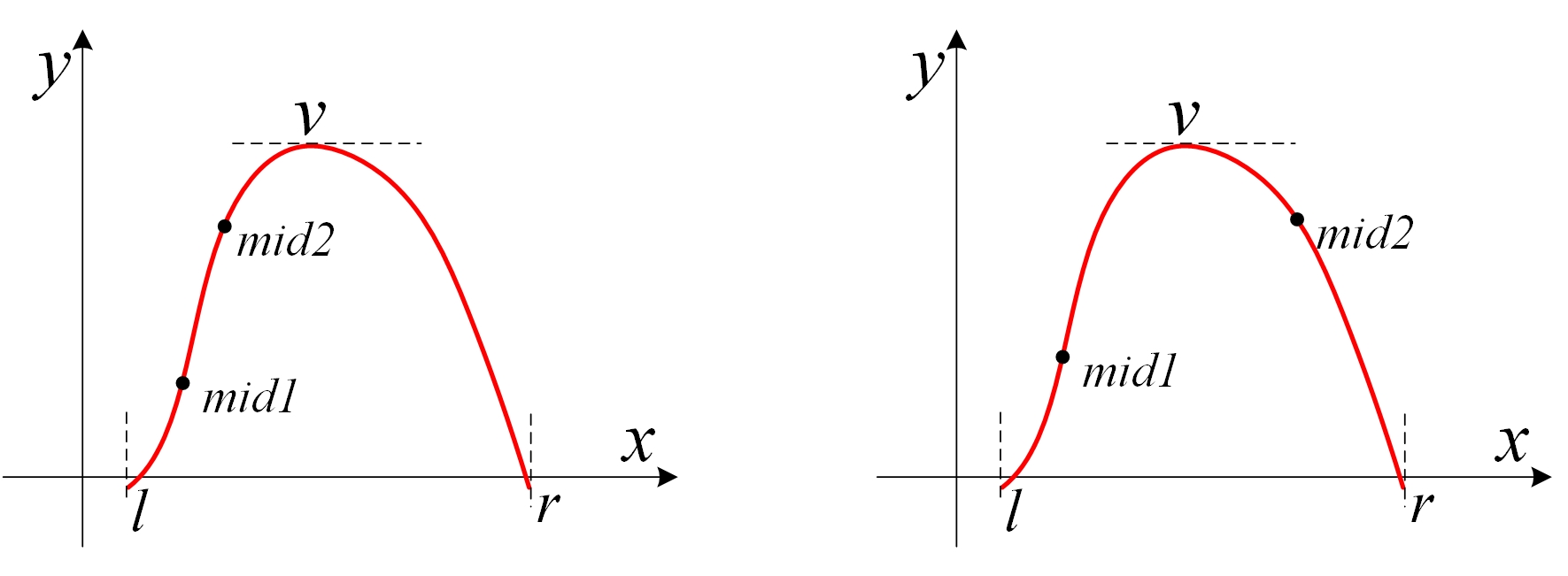
     这个时候就可以丢掉\(midl\)左边的区间了，——— 令 \(l = midl\)，然后继续分成三段

   • \(f(midl) = f(midr)\)
     这个时候两边的区间都可以丢掉了， ——— 令 \(l = midl, r = midr\)，然后继续分成三段

3. 另外一种取\(mid\)的方法：计算\([l, r]\)中间点\(mid = (l + r) / 2\)，然让\(midl\)和\(midr\)非常接近\(mid\)，例如\(midl = mid - eps，midr = mid + eps\)，其中\(eps\)是一个很小的值。那么区间每次可以减少接近一半。

例子

题目描述

如题，给出一个 \(N\) 次函数，保证在范围 \([l, r]\) 内存在一点 \(x\)，使得 \([l, x]\) 上单调增，\([x, r]\) 上单调减。试求出 \(x\) 的值。

输入格式

第一行一次包含一个正整数 \(N\) 和两个实数 \(l, r\)，含义如题目描述所示。

第二行包含 \(N + 1\) 个实数，从高到低依次表示该 \(N\) 次函数各项的系数。

输出格式

输出为一行，包含一个实数，即为 \(x\) 的值。若你的答案满足以下二者之一，则算正确：

• 你的答案 \(x'\) 与标准答案 \(x\) 的相对或绝对误差不超过 \(10^{-5}\)。
• 你的答案 \(x'\) 与标准答案 \(x\) 对应的函数值，即 $f(x') $ 和 \(f(x)\) 的相对或绝对误差不超过 \(10^{-5}\)。

样例 #1

样例输入 #1

3 -0.9981 0.5
1 -3 -3 1

样例输出 #1

-0.41421

提示

对于 \(100\%\) 的数据，\(6 \le N \le 13\)，函数系数均在 \([-100,100]\) 内且至多 \(15\) 位小数，\(|l|,|r|\leq 10\) 且至多 \(15\) 位小数。\(l\leq r\)。

【样例解释】

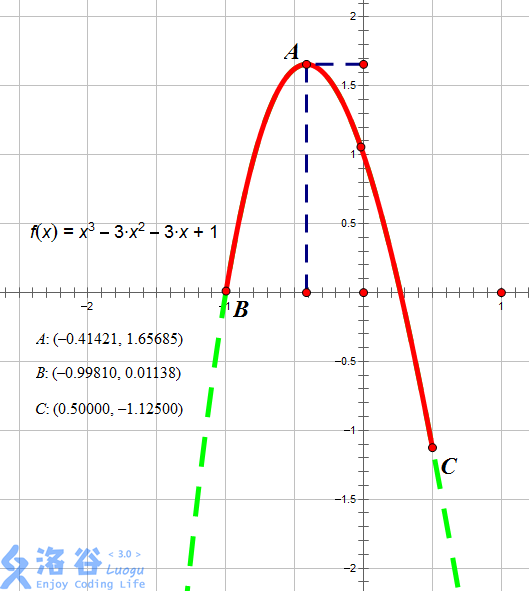
如图所示，红色段即为该函数 \(f(x) = x^3 - 3 x^2 - 3x + 1\) 在区间 \([-0.9981, 0.5]\) 上的图像。

当 \(x = -0.41421\) 时图像位于最高点，故此时函数在 \([l, x]\) 上单调增，\([x, r]\) 上单调减，故 \(x = -0.41421\)，输出 \(-0.41421\)。

写法一

void t_search(ld l, ld r)
{
    while(r - l > eps)
    {
        ld midl = l + (r - l) / 3;
        ld midr = r - (r - l) / 3;
        if (f(midl) < f(midr))
        {
            l = midl;
        }
        else if (f(midl) > f(midr))
        {
            r = midr;
        }
        else
        {
            l = midl;
            r = midr;
        }
    }
    std::cout << l;
}

写法二

void t_search2(ld l, ld r)
{
    ld mid = 0, lmid = 0, rmid = 0;
    while(r - l > eps)
    {
        mid = (l + r) / 2;
        lmid = mid - eps;
        rmid = mid + eps;
        if (f(lmid) < f(rmid))
        {
            l = mid;
        }
        else
        {
            r = mid;
        }
    }
    std::cout << l;
}

完整代码

#include <bits/stdc++.h>
#define endl '\n'
// #define int long long
using ld = long double;
using lli = long long;
const ld eps = 1e-10;
int n = 0;
ld coefficient[20];
// 秦九韶算法
ld f(ld x)
{
    ld sum = 0;
    for(int i = 0; i <= n; i++)
    sum = sum * x + coefficient[i];
    return sum; 
}

void t_search(ld l, ld r)
{
    while(r - l > eps)
    {
        ld midl = l + (r - l) / 3;
        ld midr = r - (r - l) / 3;
        if (f(midl) < f(midr))
        {
            l = midl;
        }
        else if (f(midl) > f(midr))
        {
            r = midr;
        }
        else
        {
            l = midl;
            r = midr;
        }
    }
    std::cout << l;
}

void t_search2(ld l, ld r)
{
    ld mid = 0, lmid = 0, rmid = 0;
    while(r - l > eps)
    {
        mid = (l + r) / 2;
        lmid = mid - eps;
        rmid = mid + eps;
        if (f(lmid) < f(rmid))
        {
            l = mid;
        }
        else
        {
            r = mid;
        }
    }
    std::cout << l;
}

signed main()
{
    ld l = 0, r = 0;
    std::cin >> n >> l >> r;
    for (int i = 0; i <= n; i++)
    {
        std::cin >> coefficient[i];
    }
    t_search2(l, r);
}