第四节小组学习

开营测试 B 题小贝的饭量题解

题目描述

小贝现在上六年级，正是长身体的时候，小贝的妈妈给小贝规定了每天要吃的饭量。

小贝要连续吃 $n$ 天的饭，有 $n + 1$ 个碗，第 $i$ 个碗的容量为 $a_i$，所有的碗每天都会重新盛满饭。小贝妈妈规定小贝在第 $i$ 天要吃第 $i$、$i + 1$ 两碗饭。而小贝的饭量有限，每天最多只能吃 k 的饭量。但是小贝妈妈永远都觉得小贝吃的不够多，以至于可能会有小贝吃不下的剩饭。

浪费粮食可耻！现在小贝请你帮他调整序列 $a$ 变为 $a′$，也就是减少一些碗的容量（可以不减），使得小贝每天吃饭的总量不会超过 k。但是减去的容量总和不能太大，否则小贝妈妈会觉得小贝是故意不想吃饭。

请你回答满足条件的序列 $a′$，表示调整之后每个碗的容量，并且减去的容量总和要最小。

不同的碗减去的容量可以不一样，最后每个碗的容量不可以是负数！

如果有多个满足条件的序列 $a′$ ，则输出 字典序最大 的那一个。

假设序列 $x$ 和序列 $y$ 都符合要求，则序列 $x$ 的字典序比序列 $y$ 的字典序大，当且仅当存在一个 $i$ 满足

$1≤i≤n+1$
$x_i>y_i$
对于所有的 j(1≤j<i) 均有 $x_j=y_j$

输入格式

第 $1$ 行 $2$ 个正整数 $n,k$。

第 $2$ 行 $n+1$ 个正整数表示序列 $a$。

输出格式

输出一行 $n+1$ 个整数，表示调整后的序列 $a′$。

样例

Input 1

5 6 3 4 2 7 3 1

Output 1

3 3 2 4 2 1

Input 2

5 6 7 4 3 7 2 8

Output 2

6 0 3 3 2 4

数据范围

前 50% : $1≤n≤2×10^3$ , $1≤a_i,k≤10^4$
后 50% : $1≤n≤2×10^5$, $1≤a_i,k≤10^4$

样例解释

第 $1$ 个样例中

第 $2$ 个碗容量减少了 $1$，第 $4$ 个碗容量减少了 $3$，第 $5$ 个碗容量减少了 $1$。

总共减少了 $5$ 的容量，这是最少的减少容量之和。

思路

此题重点就是输出字典序最大的。

编译结果
compiled successfully
time: 158ms, memory: 1136kb, score: 100, status: Accepted
> test 01: time: 1ms, memory: 1136kb, points: 10, status: Accepted
> test 02: time: 1ms, memory: 1136kb, points: 10, status: Accepted
> test 03: time: 1ms, memory: 1136kb, points: 10, status: Accepted
> test 04: time: 1ms, memory: 1136kb, points: 10, status: Accepted
> test 05: time: 1ms, memory: 1136kb, points: 10, status: Accepted
> test 06: time: 24ms, memory: 1136kb, points: 10, status: Accepted
> test 07: time: 35ms, memory: 1136kb, points: 10, status: Accepted
> test 08: time: 53ms, memory: 1136kb, points: 10, status: Accepted
> test 09: time: 18ms, memory: 1136kb, points: 10, status: Accepted
> test 10: time: 23ms, memory: 1136kb, points: 10, status: Accepted

#include<iostream>
using namespace std;
#define MAXN 200005

int n, a[MAXN], k;

int main() {
	cin >> n >> k;
	for(int i = 1; i <= n + 1; i ++) cin >> a[i];
	for(int i = 1; i <= n; i ++) {
		if(a[i] + a[i + 1] > k)
			if(a[i] > k) a[i] = k, a[i + 1] = 0;
			else a[i + 1] -= a[i] + a[i + 1] - k;
		else continue;
	}
	for(int i = 1; i <= n + 1; i ++) cout << a[i] << " ";
	return 0;
}

开营测评 D 题小贝的影分身题解

题目描述

小贝是一名忍者，他所在的仓前村出现了一名叛忍，叛忍藏匿在仓前村的某一个位置，现在组织要求你去追捕这名叛忍。小贝刚学会了影分身，所以他不用亲自出手，只需要派遣分身去执行任务即可。小贝可以在某些位置召唤分身，召唤的分身会赶往叛忍所在的位置实行抓捕。每个分身需要相对应的查克拉能量。此叛忍实力十分强大，所以小贝会召唤尽可能多的能够到达叛忍位置的分身，在满足这一前提下，希望消耗的查克拉能量最少。

整个仓前村可以看作一个 $n×m$ 的地图，’#‘ 表示障碍物，'.' 表示空地，’O‘ 表示叛忍，'X' 表示小贝可以召唤分身的位置。相邻位置（四连通）之间的距离为 $1$，每个分身所需要的查克拉能量值为该分身赶路的路程长度。如果有的分身位置无法到达叛忍所在地，则这些位置不必召唤分身。

请你帮小贝计算，需要放置几个分身，并且最少一共需要多少查克拉能量值。

输入格式

第 $1$ 行 $2$ 个正整数 $n 和 m$。

接下来 $n$ 行表示仓前村 $n×m$ 的地图。

输出格式

一行两个整数，分别表示需要派遣的分身数量和最少的一共需要的查克拉能量值。

样例

Input 1

4 3
O#X
X..
.X#
.#X

Output 1

3 8

数据范围
前 50%： $1≤n,m≤50$
后 50%： $1≤n,m≤2000$

思路

首先很容易看出此题是个搜索，但他是深搜还是广搜？第一问要求分身数量，很显然深搜和广搜都可以轻易完成此问题，而第二问最少能量值就需要求最短路的路径长，所以需用广搜完成搜索，并在搜索过程中进行标记每个点到终点的最短路径长。

有了这个思路，就很容易可以写出广搜代码了。

编译结果
compiled successfully
time: 500ms, memory: 23908kb, score: 100, status: Accepted
> test 01: time: 1ms, memory: 7524kb, points: 10, status: Accepted
> test 02: time: 1ms, memory: 3740kb, points: 10, status: Accepted
> test 03: time: 1ms, memory: 9672kb, points: 10, status: Accepted
> test 04: time: 1ms, memory: 9616kb, points: 10, status: Accepted
> test 05: time: 1ms, memory: 7420kb, points: 10, status: Accepted
> test 06: time: 110ms, memory: 23908kb, points: 10, status: Accepted
> test 07: time: 69ms, memory: 16928kb, points: 10, status: Accepted
> test 08: time: 188ms, memory: 23808kb, points: 10, status: Accepted
> test 09: time: 91ms, memory: 19680kb, points: 10, status: Accepted
> test 10: time: 37ms, memory: 19484kb, points: 10, status: Accepted

#include<iostream>
#include<queue>
using namespace std;
#define MAXN 2005

int n, m, x, y, ans1 = 0, ans2 = 0, num = 0;
int a[MAXN][MAXN];
char mp[MAXN][MAXN];
bool vis[MAXN][MAXN];
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};

struct node {
	int qx, qy, num;
};

void bfs(int x, int y) {
	queue<node> q;
	q.push({x, y, 0});
	a[x][y] = 0;
	vis[x][y] = true;
	while(!q.empty()) {
		for(int i = 0; i < 4; i ++) {
			node p = q.front();
			int xx = p.qx + dx[i], yy = p.qy + dy[i];
			if(xx > n || xx < 1 || yy > m || yy < 1 || vis[xx][yy] || mp[xx][yy] == '#') continue;
			a[xx][yy] = p.num + 1;
			if(mp[xx][yy] == 'X') ans1 ++, ans2 += a[xx][yy];
			q.push({xx, yy, p.num + 1});
			vis[xx][yy] = true;
		}
		q.pop();
	}
}

int main() {
	cin >> n >> m;
	for(int i = 1; i <= n; i ++) 
		for(int j = 1; j <= m; j ++) {
			cin >> mp[i][j];
			if(mp[i][j] == 'O') x = i, y = j; 
		}
	bfs(x, y);
	cout << ans1 << " " << ans2;
	return 0;
}

初赛内容：数据结构

常见的数据结构

栈（Stack）：栈是一种特殊的线性表，它只能在一个表的一个固定端进行数据结点的插入和删除操作。
队列（Queue）：队列和栈类似，也是一种特殊的线性表。和栈不同的是，队列只允许在表的一端进行插入操作，而在另一端进行删除操作。
数组（Array）：数组是一种聚合数据类型，它是将具有相同类型的若干变量有序地组织在一起的集合。
链表（Linked List）：链表是一种数据元素按照链式存储结构进行存储的数据结构，这种存储结构具有在物理上存在非连续的特点。
树（Tree）：树是典型的非线性结构，它是包括，$2$ 个结点的有穷集合 $K$。
图（Graph）：图是另一种非线性数据结构。在图结构中，数据结点一般称为顶点，而边是顶点的有序偶对。
堆（Heap）：堆是一种特殊的树形数据结构，一般讨论的堆都是二叉堆。
散列表（Hash table）：散列表源自于散列函数(Hash function)，其思想是如果在结构中存在关键字和T相等的记录，那么必定在 $F(T)$ 的存储位置可以找到该记录，这样就可以不用进行比较操作而直接取得所查记录。

详见第一节 $STL$ 中的介绍。

前中后缀表达式

前缀表达式：所有的符号都是在要运算数字的前面出现
中缀表达式：平时用的标准四则运算表达式：$9 +（3 - 1）* 3 + 10 / 2$
后缀表达式：所有的符号都是在要运算数字的后面出现
中缀表达式转化为后缀表达式：$9$ $3$ $1$ $-$ $3$ $*$ $+$ $10$ $2$ $/$ $+$
规则：从左到右遍历中缀表达式每个数字和符号，若是数字就输出，即成为后缀表达式的一部分；若是符号，则判断其与栈顶符号的优先级，是右括号或优先级低于栈顶符号（乘除优先加减）则栈顶元素依次出栈并输出，并将当前符号进栈，一直到最终输出后缀表达式为止；

树

树的定义

树是由一个集合以及在该集合上定义的一种关系构成的，集合中的元素称为树的结点，所定义的关系称为父子关系。父子关系在树的结点之间建立了一个层次结构，在这种层次结构中有一个结点具有特殊的地位，这个结点称为该树的根结点。

数据结构中有很多树的结构，其中包括二叉树、二叉搜索树、2-3树、红黑树等等，本文着重介绍二叉树。

树的基本术语

节点的度：一个节点含有的子树的个数称为该节点的度
叶节点或终端节点：度为0的节点称为叶节点
非终端节点或分支节点：度不为0的节点
双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点
兄弟节点：具有相同父节点的节点互称为兄弟节点
树的度：一棵树中，最大的节点的度称为树的度
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推
树的高度或深度：树中节点的最大层次
堂兄弟节点：双亲在同一层的节点互为堂兄弟
节点的祖先：从根到该节点所经分支上的所有节点；
子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
森林：由 $m$（$m>=0$）棵互不相交的树的集合称为森林

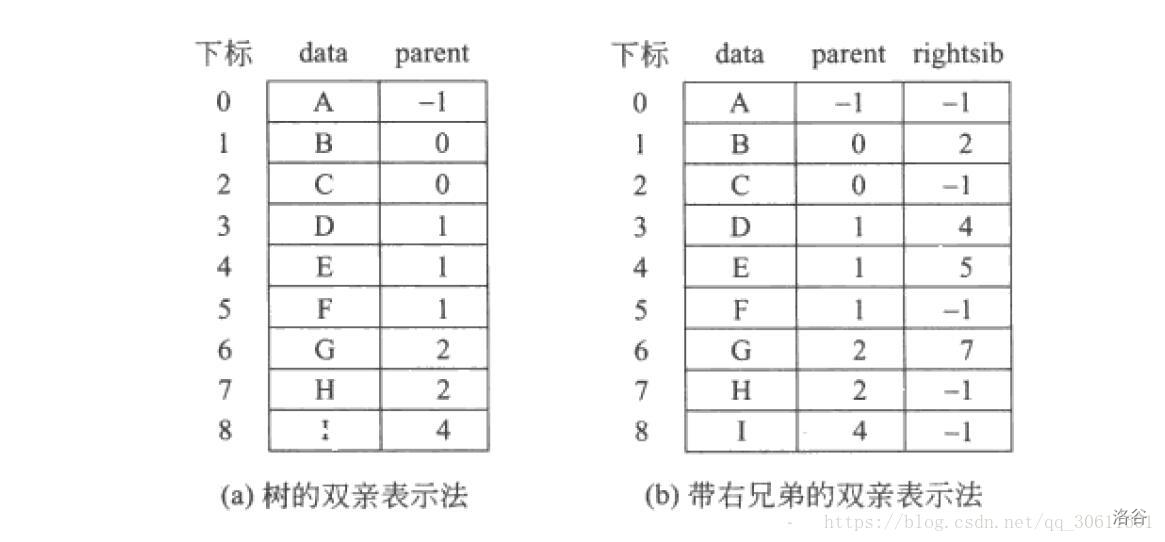
树的存储结构

双亲表示法

孩子表示法

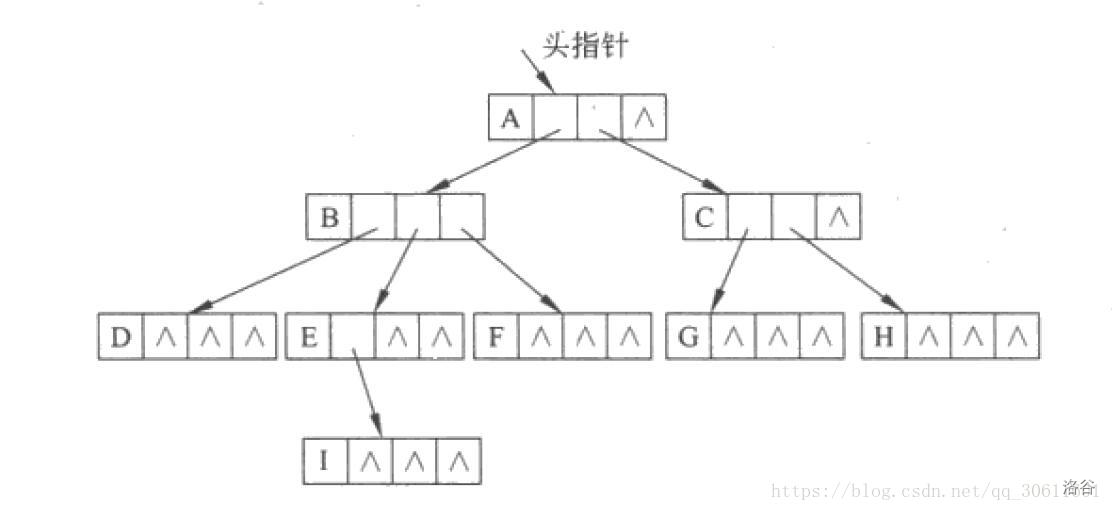
二叉树

二叉树是数据结构中一种重要的数据结构，也是树表家族最为基础的结构。

二叉树的定义：二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。

二叉树的性质

二叉树的第 $i$ 层至多有 $2 ^ {i − 1}$ 个结点；
深度为 $k$ 的二叉树至多有 $2 ^ k − 1$ 个结点；
对任何一棵二叉树 $T$ ，如果其终端结点数为 $n_0$ ，度为 $2$ 的结点数为 $n_2$ ，则 $n_0 = n_2 + 1$ 。

二叉树的实现

结构

template <class DataType>
struct BiNode
{
    DataType data;
    BiNode<DataType> * lchild,*rchild;
};

template <class DataType>
class BiTree
{
public:
    BiTree(){root = Create(root);}
    ~BiTree(){Release(root);}
    void PreOrder(){PreOrder(root);}	//前序遍历
    void InOrder(){InOrder(root);}		//中序遍历
    void PostOrder(){PostOrder(root);}	//后序遍历
private:
    BiNode<DataType> * root;
    BiNode<DataType> * Create(BiNode<DataType> *bt);
    void Release(BiNode<DataType> *bt);
    void PreOrder(BiNode<DataType> *bt);
    void InOrder(BiNode<DataType> *bt);
    void PostOrder(BiNode<DataType> *bt);
};

建立二叉树

template <class DataType>
BiNode<DataType> *BiTree<DataType>::Create(BiNode<DataType> *bt)
{
    DataType ch;
    cin>>ch;
    if(ch == '#') bt = NULL;
    else{
        bt = new BiNode<DataType>;
        bt->data = ch;
        bt->lchild = Create(bt->lchild);
        bt->rchild = Create(bt->rchild);
    }
    return bt;
}

释放二叉树

template <class DataType>
void BiTree<DataType>::Release(BiNode<DataType> *bt)
{
    if(bt != NULL){
        Release(bt->lchild);
        Release(bt->rchild);
        delete bt;
    }
}

前序遍历

template <class DataType>
void BiTree<DataType>::PreOrder(BiNode<DataType> *bt)
{
    if(bt == NULL) return;
    else{
        cout<<bt->data;
        PreOrder(bt->lchild);
        PreOrder(bt->rchild);
    }
}

中序遍历

template <class DataType>
void BiTree<DataType>::InOrder(BiNode<DataType> *bt)
{
    if(bt == NULL) return;
    else{
        InOrder(bt->lchild);
        cout<<bt->data;
        InOrder(bt->rchild);
    }
}

后序遍历

template <class DataType>
void BiTree<DataType>::PostOrder(BiNode<DataType> *bt)
{
    if(bt == NULL) return;
    else{
        PostOrder(bt->lchild);
        PostOrder(bt->rchild);
        cout<<bt->data;
    }
}

满二叉树

一棵深度为 $k$ 且有 $2 ^ k − 1$ 个结点的二叉树称为满二叉树。

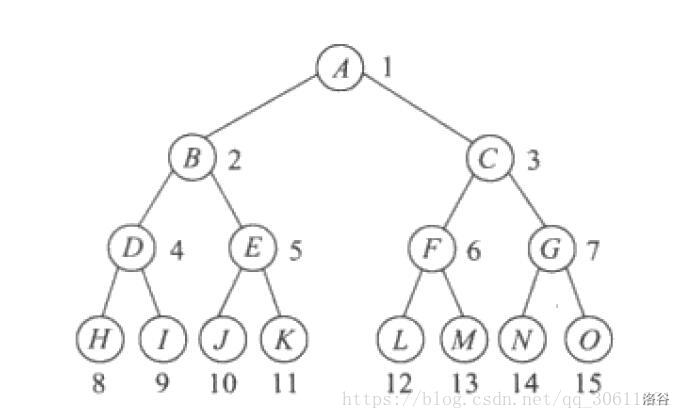
满二叉树的性质：

一颗树深度为 $h$ ，最大层数为 $k$ ，深度与最大层数相同，$k = h$

叶子数为 $2 ^ h$

第 $k$ 层的结点数是：$2 ^ {k − 1}

总结点数是：$2 ^ k − 1$ ，且总节点数一定是奇数。

完全二叉树

深度为 $k$ 的，有 $n$ 个结点的二叉树，当且仅当其每一个结点都与深度为 $k$ 的满二叉树中编号从 $1$ 至 $n$ 的结点一一对应时，称之为完全二叉树。

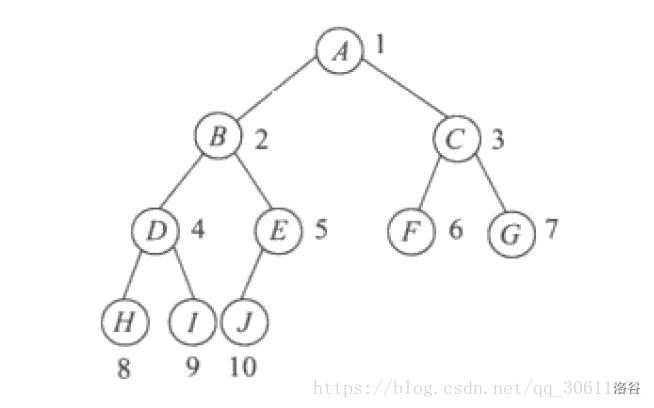
注：完全二叉树是效率很高的数据结构，堆是一种完全二叉树或者近似完全二叉树，所以效率极高，像十分常用的排序算法、$Dijkstra$ 算法、$Prim$ 算法等都要用堆才能优化，二叉排序树的效率也要借助平衡性来提高，而平衡性基于完全二叉树。

二叉排序树

二叉查找树定义：又称为是二叉排序树（Binary Sort Tree）或二叉搜索树。

二叉排序树或者是一棵空树，或者是具有下列性质的二叉树：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于或等于它的根结点的值；
它的左、右子树也分别为二叉排序树。

平衡二叉树

平衡二叉树（Balanced Binary Tree）又被称为 $AVL$ 树。它或者是一棵空树，或者是具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过 $1$。（注：平衡二叉树应该是一棵二叉排序树）

哈夫曼树

定义

给定 $N$ 个权值作为 $N$ 个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

基本术语

哈夫曼树又称最优树

哈夫曼树的构造

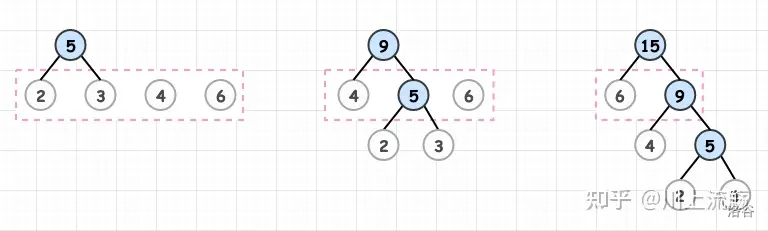
假设有 $n$ 个权值，则构造出的哈夫曼树有 $n$ 个叶子结点。 $n$ 个权值分别设为 $w_1$、$w_2$、…、$w_n$，则哈夫曼树的构造规则为：

将 $w_1$、$w_2$、…，$w_n$ 看成是有 $n$ 棵树的森林(每棵树仅有一个结点)；
在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；
从森林中删除选取的两棵树，并将新树加入森林；
重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

例如：对 2，3，4，6 这四个数进行构造

posted @ 2023-07-13 15:58 So_noSlack 阅读(110) 评论(0) 收藏举报

刷新页面返回顶部

So_noSlack 的博客

第四节小组学习

开营测试 B 题小贝的饭量题解

题目描述

输入格式

输出格式

样例

Input 1

Output 1

Input 2

Output 2

数据范围

样例解释

思路

开营测评 D 题小贝的影分身题解

题目描述

输入格式

输出格式

样例

思路

初赛内容：数据结构

常见的数据结构

前中后缀表达式

树

二叉树

哈夫曼树

公告

So_noSlack 的博客

第四节 小组学习

开营测试 B 题小贝的饭量题解

题目描述

输入格式

输出格式

样例

Input 1

Output 1

Input 2

Output 2

数据范围

样例解释

思路

开营测评 D 题小贝的影分身题解

题目描述

输入格式

输出格式

样例

思路

初赛内容 ： 数据结构

常见的数据结构

前中后缀表达式

树

二叉树

哈夫曼树

公告

第四节小组学习

初赛内容：数据结构