近期总结2024.1.24
CF981E Addition on Segments
题意:有 \(n\) 个数 \(a_{1..n}\),一开始都是 \(0\)。有 \(m\) 个操作,每个操作 \([l,r,k]\) 表示把 \(a_{l...r}\) 都加上 \(k\)。现在选其中的一些操作,求对于每个 \(i(i\in [1,n])\),是否能使得操作后 \(a_{1...n}\) 中的最大值为 \(i\)。 \(1\le n,m\le 10^4,\space 1\le l\le r\le n,\space 1\le k\le n\)
简单题,一眼秒了
北文用 bitset背包+分治,其实不需要那么麻烦。我们考虑一个数 \(a_i\) 的贡献,只选区间包含 \(i\) 的操作选出来就一定能保证 \(a_i\) 为最大值。
因此我们只考虑区间包含 \(i\) 的操作,每个操作选或不选,这个不难想到背包。
考虑从 \(i\) 到 \(i+1\) 的变化,由于是区间,在左端点加入这个区间,在右端点 \(+1\) 删掉这个区间,需要退背包。
如果是退背包,不能简单 \(0/1\)。需要算方案数,然后类似于哈希,对一个特定模数取模。时间复杂度 \(O(nm)\)。
AGC021E Ball Eat Chameleons
题意:有 \(n\) 只变色龙,可能为红色或蓝色,一开始都是蓝色。你给他们喂小球共 \(m\) 次,小球有红/蓝两种颜色。当一个变色龙已食用的红球数量大于蓝球,他会变成红色,反之亦然。求有多少个可能的喂球颜色序列,两个喂球颜色序列不同当且仅当存在一次喂的球的颜色不同,答案模 \(998244353\)。
记红色为 \(\text{R}\),蓝色为 \(\text{B}\)。我们需要计算有多少个可能的 \(\text{RB}\) 序列。
考虑序列中的任意一个 \(\text{R}\) 都可以使一个没有喂过球的变色龙变红。因此,我们可以把所有的 \(\text{R}\) 拎出来,设有 \(r\) 个 \(\text{R}\),则可以使 \(r\) 个变色龙变红。
此时序列还剩下一些 \(\text{B}\),设有 \(b\) 个,我们考虑把这些 \(\text{B}\) 和 \(\text{R}\) 合并起来。
一个变色龙喂下 \(\text{RB}\) 会变红,喂下 \(\text{BR}\) 后会变蓝。因此,我们应把每个 \(\text{B}\) 尽量和前面的一个 \(\text{R}\) 匹配起来,匹配完后剩余的 \(\text{B}\) 只能和后面的 \(\text{R}\) 组成 \(\text{BR}\),此时不满足条件,这样的 \(\text{BR}\) 和把原来的一个 \(\text{R}\) 一起组合成 \(\text{BRR}\) 才行。
综上,这样的 \(\text{RB}\) 序列能满足的变色龙数量为 \(r-b+\)组成 RB 的最大匹配数。
\(n\) 个变色龙都要满足,则 \(r-b+\)组成 RB 的最大匹配数 \(\ge n\)。
我们可以枚举 \(r\),则 \(b=m-r\),容易计算出组成 \(\text{RB}\) 的最大匹配数需要 \(\ge p=n-r+b=n+m-2r\)。
贪心思考,相当于前 \(p\) 个 \(\text{R}\) 和后 \(p\) 个 \(\text{B}\) 一定能全部匹配。
那么第 \(1\) 个 \(\text{R}\) 前面最多有 \(b-p\) 个 \(\text{B}\),第 \(2\) 个 \(\text{R}\) 前面最多有 \(b-p+1\) 个 \(\text{B}\)……
那么任意一个前缀 R 的数量\(-\)B 的数量\(<b-p+1\)
把序列对应到以 \(\text{R,B}\) 数量为横纵坐标的平面图折线,例如 \(r=6,b=6, p=2\), 合法序列为 \(rbbrbrrbbbrr\)。
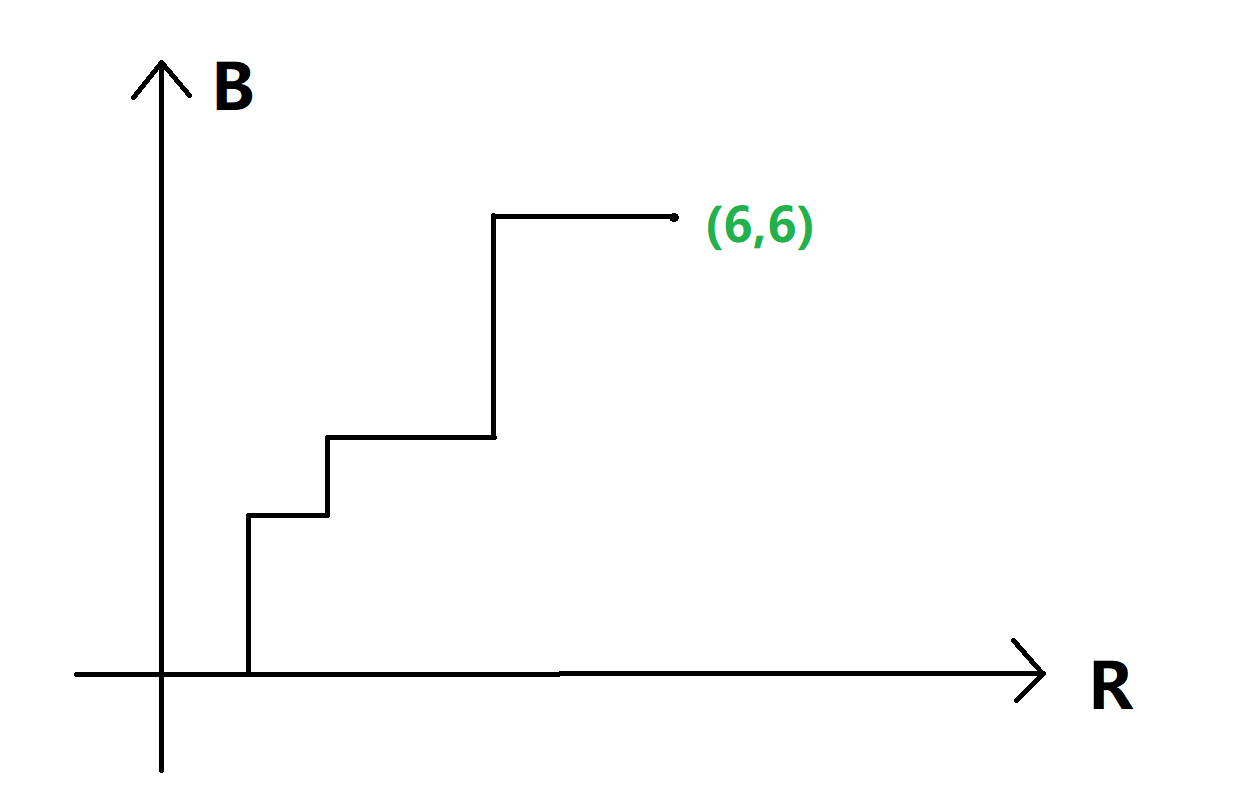
把 \(<b-p+1\) 的限制加上,相当于有一条斜率为 \(1\),截距为 \(b-p+1\) 的直线,我们的折线不能碰到这条直线。
在上图中 \(b-p+1=6-2+1=3\)。
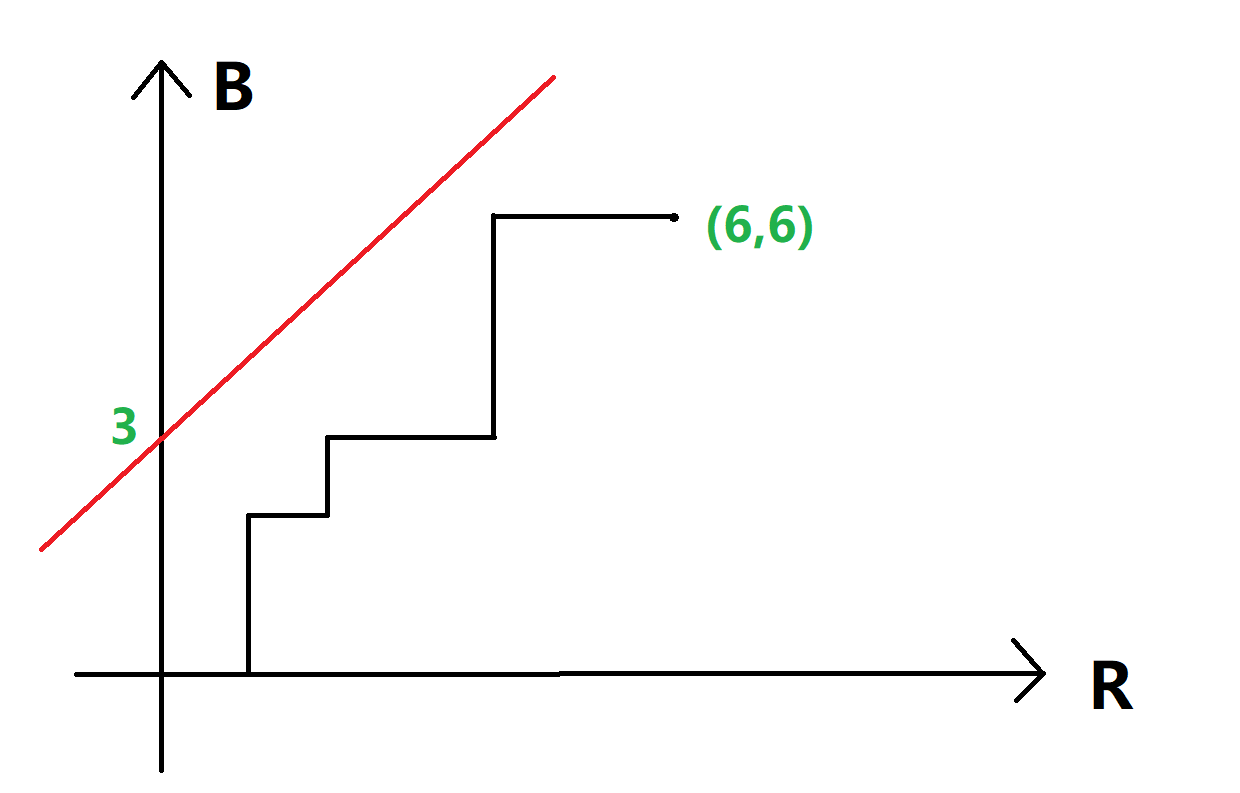
我们要算的答案就是从 \((0,0)\) 走到 \((6,6)\) 的方案数,且不碰到截距为 \(3\) 的直线。
这是一个经典的不碰线折线计数问题,这里普及一下。
考虑作 \((6,6)\) 关于这条直线的对称点,不难发现为 \((3,9)\),我们考虑一条从 \((0,0)\) 到 \((3,9)\) 的折线。
取出这条折线与直线的第一个交点,把交点后面的部分沿直线作对称。
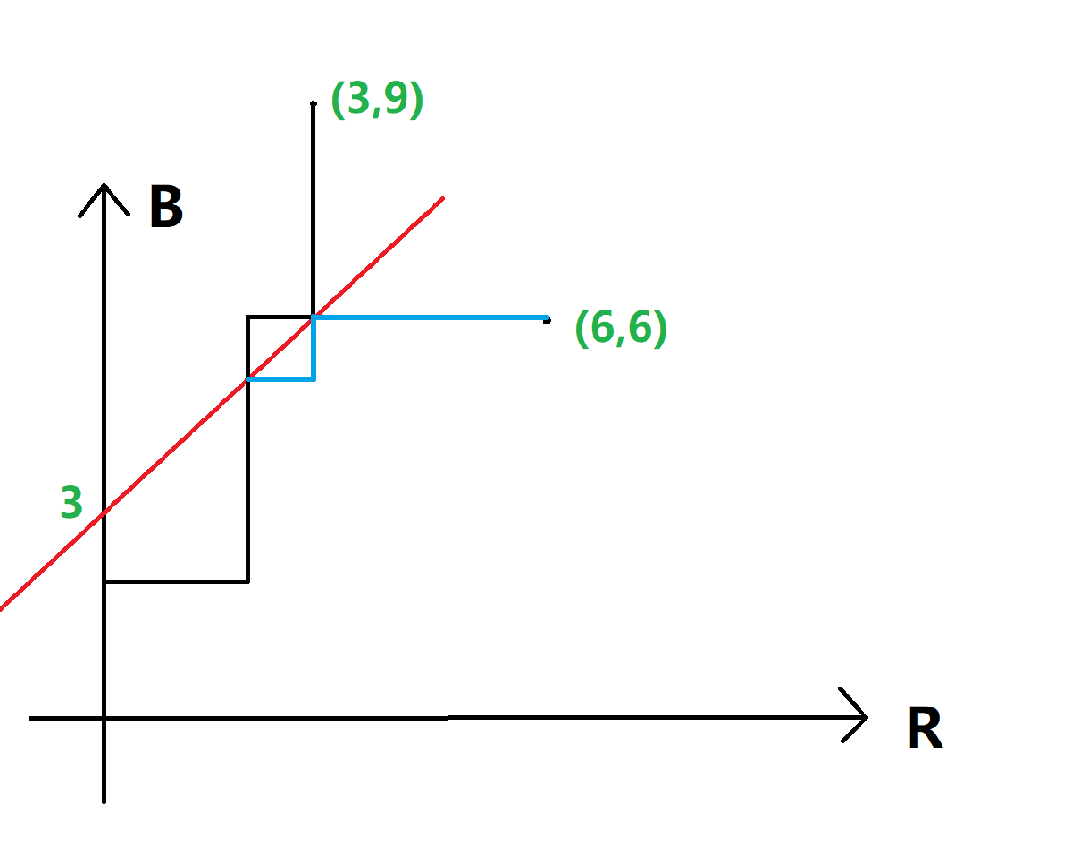
不难发现其实这就是一条碰到直线的折线,因此碰到/穿过直线的到达 \((6,6)\) 的折线数量就是 \((0,0)\to (3,9)\) 的折线数量,这个容易用组合数算。
因此,对于一条截距为 \(b-p+1\) 的直线,算有多少条 \((0,0)\to (r,b)\) 的不碰到直线的折线,作 \((r,b)\) 对称点 \((p-1,b+r-p+1)\),组合数算即可。注意直线在 \((0,0)\) 下方的情况。
时间复杂度 \(O(n)\)。
CF568E Longest Increasing Subsequence
题意:给出一个长度为 \(n\) 的序列 \(a_{1...n}\),其中有些位置是空的,记有 \(k\) 个空位置。给出 \(m\) 和 \(m\) 个正整数,你需要把这 \(m\) 个数选 \(k\) 个填入空位置,满足填完后 \(a\) 的最长严格上升子序列最大,求填完后的 \(a\),输出任意一个合法的答案即可。\(1\le n,m\le 10^5,\space 1\le k\le \min(10^3,m)\)
报表,实际上不需要 \(k\le 10^3\) 这个条件。
考虑可以 \(\text{DP}\) 出这个最长上升子序列。先在 \(a\) 的前面加一个 \(0\),后面加一个 \(+\infty\),在 \(m\) 个数中加入一个 \(+\infty\)。
然后把这 \(m+1\) 个数排个序,并去重。
预处理 \(c_i\) 表示 \(a_{1...i}\) 中的空位数,\(x_i,y_i\) 表示 \(a_i\) 在 \(m+1\) 中的严格前驱后继分别排第几。
设 \(f[i]\) 表示对于 \(a_i\) 非空的 \(i\),以 \(i\) 结尾的最长上升子序列长度。
把 \(\min\) 拆掉,分成两部分:
然后 \(c_i-c_j\le x_i-y_j+1 \Longleftrightarrow x_i-c_i\ge y_j-c_j-1\),\(x_i-y_j+1\le c_i-c_j \Longleftrightarrow c_i-x_i\ge c_j-y_j+1\)
直接 \(\text{cdq}\) 即可,最后方案随便搞搞即可,时间复杂度 \(O(n\log^2 n)\)。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号