近期总结2024.1.23

CF1097G Vladislav and a Great Legend

题意：一棵有 \(n\) 个点的树，设 \(w(S)\) 为使点集 \(S\) 连通的最小边数。给定 \(k\)，求 \(\sum\limits_{S} w^k(S)\pmod {10^9+7}\)。\(1\le n\le 10^5,\space 1\le k\le 200\)

---

考虑第二类斯特林数：

\[\begin{aligned} \sum_S w^k(S) &= \sum_S \sum_{i=0}^{\min(w(S),k)} {w(S) \choose i} {k \brace i} i! \\ &= \sum_{i=0}^k {k \brace i} i! \sum_S {w(S) \choose i} \end{aligned} \]

我们只需要求对于每个 \(i\)，\(\sum\limits_S {f(S) \choose i}\) 的值。

这个式子意思是对于所有的 \(S\)，选对应连通块中的 \(i\) 条边的方案数，其实就是树上背包。

设 \(f[u,i]\) 表示在 \(u\) 子树中考虑了包含 \(u\) 的所有连通块，选其中 \(i\) 条边的方案数总和。

然后乱 DP 一波即可，根据经典结论，时间复杂度为 \(O(nk)\)。

---

AGC030F Permutation and Minimum

题意：给出 \(n\)，有一个 \(1...2n\) 的排列 \(a\)，部分数字未知。现在将排列 \(a\) 填完，设 \(b_i=\min_(a_{2i-1},a_{2i})\)，问可以得到多少种不同的 \(b\) 序列，模 \(10^9+7\)。 \(1\le n\le 300\)

---

首先，若 \(a_{2i-1}\) 和 \(a_{2i}\) 都已知，那么 \(b_i\) 可以直接确定，我们把这些位置扔掉。

那么 \(a\) 中剩下的，对于位置 \(2i-1\) 和 \(2i\)，对应的数字要么已确定、一个未知，要么都是未知。

由于 \(b_i\) 的取值只和最小值有关，考虑把数字从大到小填入 \(a\)。填的过程中，可能有的数字已经确定位置，有的未确定，我们不可能把两个位置一确定的数放在同一组（一组定义为 \(2i-1\) 和 \(2i\)）。

设 \(f[i,j,k]\) 表示填了后 \(i\) 个数字，这 \(i\) 个数字中还未和其他数字匹配在一组的有 \(j+k\) 个，其中 \(j\) 个位置未确定，\(k\) 个已确定。

转移先考虑这个数是否已确定。

若已确定，他有两种选择：

• 和一个更小的数字分在同一组：\(f[i,j,k+1]\gets f[i-1,j,k]\)

• 和之前一个较大的数分在同一组，这个数是 \(j\) 个中的一个：\(f[i,j-1,k]\gets f[i-1,j,k]\)

若未确定，也有两种选择：

• 和一个更小的数字分在同一组：\(f[i,j+1,k]\gets f[i-1,j,k]\)

• 和之前一个较大的未知位置的数分在同一组，设有两个未知数字的组，除去之前已占用的组个数为 \(b\)（可以算出来）：\(f[i,j-1,k]\gets f[i-1,j,k]\times b\)

• 和之前一个较大的已知位置的数分在同一组：\(f[i,j,k-1]\gets f[i-1,j,k]\)

时间复杂度 \(O(n^3)\)。

---

CF516D Drazil and Morning Exercise

题意：一棵树，\(n\) 个点，有边权。对于点 \(u\)，设 \(d_u=\max\limits_v \{\text{dist}(u,v)\}\)。有 \(q\) 次询问，每次给出一个 \(k\)，找一个连通块 \(S\)，满足 \(\max\limits_{u\in S}\{d_u\}-\min\limits_{u\in S}\{d_u\}\le k\)，求最大的 \(|S|\)。 \(1\le n\le 10^5,\space 1\le q\le 50\)

---

考虑一棵树的“中心”，设其为点 \(r\)，满足 \(d_r\) 是 \(d_{1...n}\) 中最小的。类似于重心，我们可以证明 \(d\) 最小的点至多有 \(2\) 个。

以点 \(r\) 为根，不难发现，对于点 \(u(u\not =r)\)，设其父亲为 \(f\)，总有 \(d_u\le d_f\)，一个点的祖先的 \(d\) 总是 \(\ge\) 他的 \(d\)。

考虑直接把树遍历一遍，扫到一个点 \(u\) 时，通过二分得出他能贡献到的一条链，差分即可。

时间复杂度 \(O(qn\log n)\)，用双指针代替二分可以做到 \(O(qn)\)。

---

CF1149D Abandoning Roads

题意：一张无向连通图，有 \(n\) 个点和 \(m\) 条边，边权只有 \(a,b\) 两种，对于每个 \(1\le i\le n\)，求所有可能的最小生成树中 \(\text{dist}(1,i)\) 的最小值。

\(1\le n\le 70,\space n-1\le m\le 200,\space 1\le a<b\le 10^7\)

---

删去所有的边权为 \(b\) 的边，会剩下一些连通块，每条边权值都是 \(a\)。

显然，一个连通块内的点互相到达时，只能走权值为 \(a\) 的边。

如果需要在多个连通块内互相到达，需要经过权值为 \(b\) 的边。

可以用并查集来维护所有连通块，然后跑最短路。每次遍历一条边时，检查两点是否处于同一个连通块。仅仅如此，我们仍然无法保证“同一个连通块只走权值为 \(a\) 的边”这个条件。

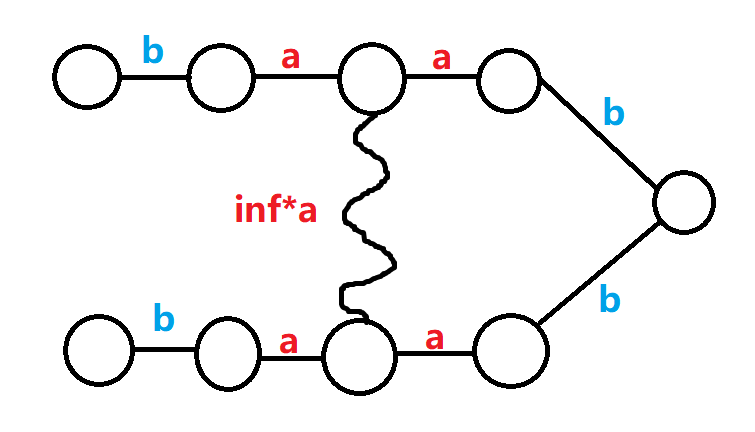
如图，按照上述的方式跑最短路，会经过右边的部分，经过两条权值为 \(b\) 的边后又回到了原来的连通块，这样是错误的。

因此，为了防止回到原来的连通块，需要状态压缩记录经过的连通块编号，时间复杂度 \(O(2^nnm\log m)\)。

不难发现点数 \(\le 3\) 的连通块无需考虑可能走回的情况，实际上只有 \(\frac n4\) 个连通块需要记录，时间复杂度 \(O(2^{\frac n4}nm\log m)\)。

由于边权只有两种，可以开两个队列来 BFS，一个满足头尾 \(\le a\)，一个满足头尾 \(\le b\)，每次取两个队头中最小的，遍历权值为 \(a\) 的边后加入第一个队列，\(b\) 的加入第二个队列。

时间复杂度 \(O(2^{\frac n4}m)\)。