[题解]P14469 [COCI 2025/2026 #1] 皇后 / Kraljica

P14469 [COCI 2025/2026 #1] 皇后 / Kraljica

怎么连剪枝都不会写了（哭）

---

可以想到用 BFS 求解。对于位置 \((x,y)\)，八方向枚举走到的位置进行扩展。

状态数是 \(O(nm)\) 的，但是转移是 \(O(n+m)\) 的，不剪枝过不去。

考虑到同一直线（八方向）上的元素两两间可以一步到达。

所以对于某一方向能走到的 \((x',y')\)，若 \(f[x][y]\ge f[x'][y']\)，就直接结束这个方向的求解，这是因为该直线上的元素已经有 \(f[x'][y']\) 进行更新了。

为什么不是 \(f[x][y]+1\ge f[x'][y']\)？因为转移方向不同，拿样例二举例：

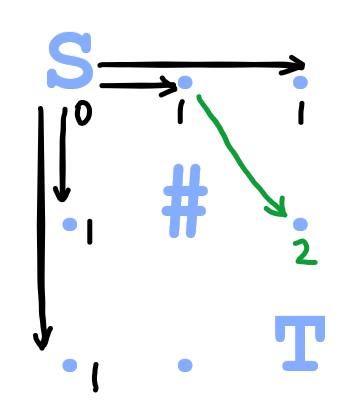
如果接下来从 \((1,3)\) 向下扩展，到 \((2,3)\) 就会 break 掉。\((3,3)\) 从 \((2,3)\) 转移过来，答案就变成 \(3\) 了。

如果将传送门看作权值为 \(0\) 的边，可以采用 01-BFS 求解。或者在扩展到的位置判断是否为传送门，这样边权就全是 \(1\) 了，普通 BFS 即可解决。

01-BFS

#include<bits/stdc++.h>
#define C (s[x][y])
#define _C (s[i][j])
using namespace std;
const int N=1005;
int n,m,tx,ty,dx[8]{-1,-1,-1,0,1,1,1,0},dy[8]{-1,0,1,1,1,0,-1,-1};
int px[10],py[10],f[N][N],inf;
string s[N];
struct Node{int x,y;}tmp[10];
deque<Node> q;
signed main(){
	memset(f,0x3f,sizeof f),inf=f[0][0];
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	s[0].resize(m+2,'#'),s[n+1].resize(m+2,'#');
	for(int i=1;i<=n;i++) cin>>s[i],s[i]='#'+s[i]+'#';
	for(int x=1;x<=n;x++){
		for(int y=1;y<=m;y++){
			if(C=='S') f[x][y]=0,q.emplace_back(Node{x,y});
			else if(C=='E') tx=x,ty=y;
			else if(C>='1'&&C<='9'){
				px[C-'1']+=x,py[C-'1']+=y;
			}
		}
	}
	while(!q.empty()){
		if(f[tx][ty]^inf) break;
		Node t=q.front();
		q.pop_front();
		int i=t.x,j=t.y,d=f[i][j];
		for(int p=0;p<8;p++){
			int x=i,y=j;
			while(1){
				x+=dx[p],y+=dy[p];
				if(d>=f[x][y]) break;//剪枝
				if(f[x][y]^inf) continue;
				if(C=='#') break;
				f[x][y]=d+1,q.push_back(Node{x,y});
			}
		}
		if(_C>='1'&&_C<='9'){
			int x=px[_C-'1']-i,y=py[_C-'1']-j;
			if(f[x][y]==inf) f[x][y]=d,q.push_front(Node{x,y});
		}
	}
	cout<<(f[tx][ty]==inf?-1:f[tx][ty])<<"\n";
	return 0;
}

BFS

#include<bits/stdc++.h>
#define C (s[x][y])
using namespace std;
const int N=1005;
int n,m,tx,ty,dx[8]{-1,-1,-1,0,1,1,1,0},dy[8]{-1,0,1,1,1,0,-1,-1};
int px[10],py[10],f[N][N],inf;
string s[N];
struct Node{int x,y;}tmp[10];
queue<Node> q;
signed main(){
	memset(f,0x3f,sizeof f),inf=f[0][0];
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	s[0].resize(m+2,'#'),s[n+1].resize(m+2,'#');
	for(int i=1;i<=n;i++) cin>>s[i],s[i]='#'+s[i]+'#';
	for(int x=1;x<=n;x++){
		for(int y=1;y<=m;y++){
			if(C=='S') f[x][y]=0,q.emplace(Node{x,y});
			else if(C=='E') tx=x,ty=y;
			else if(C>='1'&&C<='9'){
				px[C-'1']+=x,py[C-'1']+=y;
			}
		}
	}
	while(!q.empty()){
		if(f[tx][ty]^f[0][0]) break;
		Node t=q.front();
		q.pop();
		int i=t.x,j=t.y,d=f[i][j];
		for(int p=0;p<8;p++){
			int x=i,y=j;
			while(1){
				x+=dx[p],y+=dy[p];
				if(C=='#') break;
				if(f[x][y]<=d) break;//剪枝
				if(f[x][y]==inf) f[x][y]=d+1,q.push(Node{x,y});
				if(C>='1'&&C<='9'){
					int xx=px[C-'1']-x,yy=py[C-'1']-y;
					if(d+1<f[xx][yy]){
						f[xx][yy]=d+1;
						q.push(Node{xx,yy});
					}
				}
			}
		}
	}
	cout<<(f[tx][ty]==inf?-1:f[tx][ty])<<"\n";
	return 0;
}