[题解]G. Puzzle II - The 3rd Universal Cup. Stage 2: Zielona Góra

#8523. Puzzle II

四句话题意

给定两个长由黑白球组成的环，每个环有 \(n\) 个球，且黑球和白球的总数都是 \(n\)。

你可以进行最多 \(n\) 次操作，每次操作选定两个环上长度恰为 \(k\) 的区间交换。

最终要使两个环都变成单色的。

请构造这个操作序列，无需最小化操作次数。

Solution

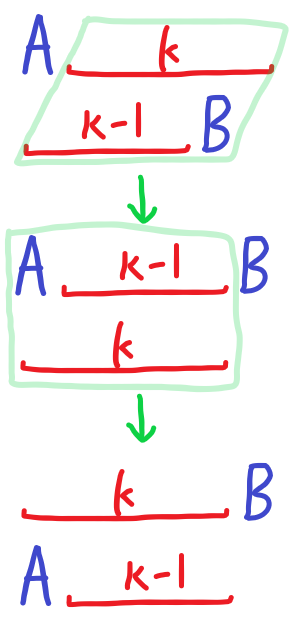
上图中，我们做了什么？

我们发现，可以使用两次交换，将 A, B 两球换到了对方的环上，而其他球所在的环不变。

显然必有一个环上的黑球 \(\le\dfrac{n}{2}\)，不妨设是第一个环。每次操作将环一的黑球换到环二去，那么操作总数 \(\le 2\times \dfrac{n}{2}=n\)。所以必然能构造出来。

我么将环一上的黑球，环二上的白球记录下来。

然后我们发现，每次交换会让部分球变动一下位置，可以用树状数组找变动的区间，以及区间修改。

找变动区间如果用树状数组上倍增，是 \(O(n\log n)\) 的。

因为不好实现所以在树状数组外二分求的，是 \(O(n\log^2 n)\) 的。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int n,k,c,c1,c2;
string a,b;
inline int lb(int x){return x&-x;}
inline int adj(int x){return (x>n?x-n:(x<1?x+n:x));}
struct BIT{
	int s[N];
	inline void chp(int x,int v){for(;x<=c;x+=lb(x)) s[x]+=v;}
	inline int qry(int x){int a=0;for(;x;x-=lb(x)) a+=s[x];return a;}
}p1,p2;
inline void solve(int x,int y){
	int z1=p1.qry(x),z2=p2.qry(y);
	cout<<adj(z1+1)<<" "<<adj(z2-k+1)<<"\n"<<z1<<" "<<adj(z2-k+1)<<"\n";
	int l=x,r=c1;
	while(l^r){
		int mid=(l+r+1)>>1;
		if(p1.qry(mid)<=z1+k) l=mid;
		else r=mid-1;
	}
	p1.chp(x,-1),p1.chp(l+1,1);
	l=1,r=y;
	while(l^r){
		int mid=(l+r)>>1;
		if(p2.qry(mid)>=z2-k+1) r=mid;
		else l=mid+1;
	}
	p2.chp(l,1),p2.chp(y,-1);
}//x,y是否修改无影响
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>k>>a>>b;
	for(char i:a) c+=(i=='B');
	if(2*c>n){//保证A中黑球更少
		c=n-c;
		for(char &i:a) i^=1;
		for(char &i:b) i^=1;
	}
	cout<<2*c<<"\n";
	for(int i=1;i<=n;i++){
		if(a[i-1]=='B') p1.chp(++c1,i),p1.chp(c1+1,-i);
		if(b[i-1]=='C') p2.chp(++c2,i),p2.chp(c2+1,-i);
	}
	for(int i=1;i<=c1;i++){
		solve(i,c1-i+1);//x从前往后 y从后往前
	}//这样就相当于把遍历过的位置在BIT上删掉了
	return 0;
}

\(O(n)\) 做法稍后补。