[笔记]数位 DP
前
大概一年半前写过数位 DP 的笔记,忘挺快的,并且考虑到之前的 \(2\) 篇笔记(上 下)语言稚嫩、公式混乱、码风清奇(其实还好),有些许地方言不达意,所以打算从头梳理一下,并且对若干题目进行方法归纳、深入思考。
会不定期更新。
附上题单:https://www.luogu.com.cn/training/82023
算法简述
数位 DP 一般用于求解 \([L,R]\) 中满足条件 \(f(i)\) 的 \(i\) 的个数、数字和、总和等等。
通常 \(L,R\) 会很大,甚至超过 long long,直达 \(10^{10^5}\) 之类的天文数字。所以数位 DP 可能算最容易辨认的 DP 了(真的
顾名思义,数位 DP 的核心思想就是按位 DP,因此复杂度通常与数的位数有关,而非数的大小。
许多 \(f(i)\) 的判定需要记录很多的上下文信息,因此我们一般使用记忆化搜索来实现数位 DP。
例题
P4999 烦人的数学作业
我们写数位 DP,通常会利用前缀和的思想,将 \([L,R]\) 的答案转化为 \([1,R]\) 的答案减去 \([1,L-1]\) 的答案,故我们仅需考虑 \([1,x]\) 内的答案如何计算。
由于是按位进行,我们必须在搜索过程中记录当前正在填写的位置 \(pos\)。一般从最高位 \(len\) 填起,到第 \(1\) 位结束。
为了要让枚举的数都 \(\le x\),我们需要额外记录一个 bool 类型的 \(limit\),表示当前位的填写有没有限制。
拿 \(x=520\) 举例:
- 如果最高位填写 \(0\sim 4\),那么后面可以随便填没有限制。
- 如果最高位填写 \(5\),那么下一位就要受限,如果填 \(0\sim 1\) 就是第一条,填 \(2\) 就是第二条,这样循环下去直到填完……
另外我们要记录 \(sum\),表示 \(pos+1\) 到最高位的数位和是多少,在递归结束时返回。
然而我们把代码一写,这不还是暴搜嘛?
其实我们发现,两个状态的 \(pos,sum\) 都分别相等时,它们的返回值也将完全一样。因此我们可以用 \(f[pos][sum]\) 来记忆化。
不过需要注意的是,只有 \(limit=0\) 时才可以记忆化,因为填写是否受限会导致答案不同。这样做能保证时间不退化,是因为 \(limit=1\) 的状态在递归树上只是一条链而已。
数位 DP 的时间复杂度就是状态数量(\(f\) 可能被用到的位置个数),乘上转移的复杂度。
这样,此算法的时间复杂度就是 \(O(B\times \log_B N)\times O(B)+O(T)=O(T+B^2\log_B N)\),可以通过。
其中 \(N\) 与 \(L,R\) 同阶,\(B=10\) 表示进制。
点击查看代码 - R233800485
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=20,P=1e9+7;
int f[N][9*N],a[N],t,l,r;
int dfs(int p,bool lim,int s){//pos,limit,sum
if(!p) return s;
if(!lim&&f[p][s]) return f[p][s];
int rig=lim?a[p]:9,ans=0;
for(int i=0;i<=rig;i++){
ans+=dfs(p-1,lim&&i==rig,s+i);
}
ans%=P;
if(!lim) f[p][s]=ans;
return ans;
}
int solve(int x){//将 x 的每一位存在 a 中,更方便
int len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,1,0);
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>t;
while(t--){
cin>>l>>r;
cout<<(solve(r)-solve(l-1)+P)%P<<"\n";
}
return 0;
}
学到的:用前缀和思想来统计;数位 DP 的基本框架;数位 DP 的思考方向(先打暴搜,再考虑记忆化)。
Tip:上下文信息中如果有数组,我们一般将其定义为全局数组,利用回溯来传递,而非作为参数传递,以节省空间。
P2602 [ZJOI2010] 数字计数
依照上题的思路,我们先把暴搜一写,再想怎么记忆化。
不过这暴搜思路也有两种:
- 一次暴搜同时统计 \(10\) 个位置。
- \(10\) 次暴搜,每次统计一位。
我们发现,前者将 \(10\) 个数字的填写情况看作整体,状态数量太多,不容易记忆化。相比之下,后者仅需记录某个数字的填写次数 \(cnt\),更容易优化。
这样我们的记忆化数组顺理成章地写成 \(f[pos][cnt]\)。
需要注意的是统计 \(0\) 的答案时,前导 \(0\) 不应记入 \(cnt\)。为此我们在上下文信息中额外记录一个 bool 类型的 \(zero\),表示 \(p+1\) 到最高位是否全都是 \(0\)。
相应地,只有 \(zero=0\) 且 \(limit=0\) 时才能使用记忆化,原因同上。
时间复杂度 \(O(B)\times O(\log^2_B N)\times O(B)=O(B^2\log^2_B N)\)。
点击查看代码 - R233311222
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=15;
int x,a[N],f[N][N];
int dfs(int p,int c,bool lim,bool zro){//pos,cnt,limit,zero
if(!p) return c;
if(!lim&&!zro&&(~f[p][c])) return f[p][c];
int rig=lim?a[p]:9,ans=0;
for(int i=0;i<=rig;i++){
ans+=dfs(p-1,c+(i==x&&(i||!zro)),lim&&i==rig,zro&&!i);
}
if(!lim&&!zro) f[p][c]=ans;
return ans;
}
int solve(int x){
int len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,0,1,1);
}
signed main(){
int l,r;
cin>>l>>r;
for(x=0;x<=9;x++){
memset(f,-1,sizeof f);
cout<<solve(r)-solve(l-1)<<" ";
}
}
学到的:逐个数字计算答案;对前导 \(0\) 的处理。
P6218 [USACO06NOV] Round Numbers S
用 \(dif\) 记录 \(pos+1\) 到最高位 \(0\) 与 \(1\) 个数的差值。
用 \(f[pos][dif]\) 来记忆化即可,具体实现中由于 \(dif\) 可能存在负数所以需要加上一个偏移量。
注意处理前导 \(0\)。
时间复杂度 \(O(B\log^2_B n)\)。
点击查看代码 - R233314031
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=35;
int a[N],f[N][N<<1];
int dfs(int p,int d,bool lim,bool zro){
if(!p) return d>=0;
if(!lim&&!zro&&(~f[p][d+N])) return f[p][d+N];
int rig=lim?a[p]:1,ans=0;
for(int i=0;i<=rig;i++){
ans+=dfs(p-1,d+(!zro||i)*(i?-1:1),lim&&i==rig,zro&&!i);
}
if(!lim&&!zro) f[p][d+N]=ans;
return ans;
}
int solve(int x){
int len=0;
while(x) a[++len]=x&1,x>>=1;
return dfs(len,0,1,1);
}
signed main(){
memset(f,-1,sizeof f);
int l,r;
cin>>l>>r;
cout<<solve(r)-solve(l-1);
return 0;
}
P13085 [SCOI2009] windy 数(加强版)
我们发现每一位的填写情况仅与上一位 \(last\) 有关,所以用 \(f[pos][last]\) 来记忆化即可。
注意处理前导 \(0\) 的问题,在 \(pos+1\) 到最高位全都是 \(0\) 的情况下,\(pos\) 可以随意填,与 \(last\) 无关。
时间复杂度 \(O(B\log n)\times O(B)=O(B^2\log N)\)。
点击查看代码 - R233813690
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=20;
int a[N],f[N][10];
int dfs(int p,int lst,bool lim,bool zro){
if(!p) return 1;
if(!lim&&!zro&&(~f[p][lst])) return f[p][lst];
int rig=lim?a[p]:9,ans=0;
for(int i=0;i<=rig;i++){
if(!zro&&abs(i-lst)<2) continue;
ans+=dfs(p-1,i,lim&&i==rig,zro&&!i);
}
if(!lim&&!zro) f[p][lst]=ans;
return ans;
}
int solve(int x){
int len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,0,1,1);//一开始 lst 随便写就可以
}
signed main(){
memset(f,-1,sizeof f);
int l,r;
cin>>l>>r;
cout<<solve(r)-solve(l-1)<<"\n";
return 0;
}
CF1036C Classy Numbers
显然可以用 \(f[pos][cnt]\) 记忆化,其中 \(cnt\) 是截至目前填写的非零数字个数。
不需要处理前导 \(0\)。
点击查看代码 - #336491804
#include<bits/stdc++.h>
#define pc(x) __builtin_popcount(x)
using namespace std;
typedef long long ll;
const int N=20;
ll t,l,r,f[N][N];
int len,a[N];
inline ll dfs(int p,bool lim,int cnt){
if(cnt>3) return 0;
if(!p) return 1;
if(!lim&&(~f[p][cnt])) return f[p][cnt];
int rig=lim?a[p]:9;ll ans=0;
for(int i=0;i<=rig;i++){
ans+=dfs(p-1,lim&&i==rig,cnt+(i!=0));
}
if(!lim) f[p][cnt]=ans;
return ans;
}
inline ll solve(ll x){
len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,1,0);
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
memset(f,-1,sizeof f);
cin>>t;
while(t--){
cin>>l>>r;
cout<<solve(r)-solve(l-1)<<"\n";
}
return 0;
}
CF628D Magic Numbers
奇数偶数位的限制仅需在搜索的同时限制一下就行了。
\(m\mid x\) 的条件,仅需搜索过程中记录当前填写的数值 \(\bmod\) \(m\) 的结果,记为 \(num\)。\(f[pos][num]\) 用于记忆化就可以了。注意这种写法仅适用于单测,若为多测则需要额外添加一维,表示当前位数的奇偶性。
实现细节上,注意 \(l,r\) 足足有 \(2000\) 位,所以需要用字符串存,然而字符串 \(-1\) 不好实现,所以可以先计算 solve(r)-solve(l),然后特判 \(l\) 是否合法,合法就额外 \(+1\)。
点击查看代码 - #336496736
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e3+2,M=2001,P=1e9+7;
int m,d,len,a[N],f[N][2][M];//因为没有多测,所以第二维可以去掉
string l,r;
inline int dfs(int p,bool lim,int s){
if(!p) return !s;
int& g=f[p][(len-p)&1][s];
if(!lim&&(~g)) return g;
int rig=lim?a[p]:9;ll ans=0;
if((len-p)&1){
if(d<=rig) ans=dfs(p-1,lim&&d==rig,(s*10+d)%m);
}else{
for(int i=0;i<=rig;i++){
if(i==d) continue;
ans+=dfs(p-1,lim&&i==rig,(s*10+i)%m);
}
}
ans%=P;
if(!lim) g=ans;
return ans;
}
inline int solve(string x){
len=x.size();
for(int i=0;i<len;i++) a[len-i]=x[i]-'0';
return dfs(len,1,0);
}
inline bool check(string x){
len=x.size();
for(int i=1;i<len;i+=2) if(x[i]-'0'!=d) return 0;
for(int i=0;i<len;i+=2) if(x[i]-'0'==d) return 0;
int s=0;
for(char i:x) s=(s*10+i-'0')%m;
return !s;
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
memset(f,-1,sizeof f);
cin>>m>>d>>l>>r;
cout<<(solve(r)-solve(l)+check(l)+P)%P<<"\n";
return 0;
}
学到的:数位太多存不下时,可以先计算
solve(r)-solve(l),然后特判 \(l\) 是否合法。
SP10606 BALNUM - Balanced Numbers
很暴力也很好想的记忆化思路,记数字 \(i\) 的访问情况 为 \(vis[i]\),访问次数的奇偶性 为 \(sta[i]\)。
将 \(vis,sta\) 都压成 \([0,2^{10})\) 的整数,然后用 \(f[pos][vis][sta]\) 来记忆化,即可通过。
注意前导 \(0\) 的处理,并开 ull。
点击查看代码 - R233816509
#include<bits/stdc++.h>
#define int unsigned long long
const int N=20;
using namespace std;
int t,l,r,len,a[N],vis,sta,f[N][1024][1024];
bitset<1024> fv[N][1024];
int dfs(int p,bool lim,bool zro){
if(!p){
for(int i=0;i<=9;i++) if(((vis>>i)&1)&&((sta>>i)&1)==(i&1)) return 0;
return 1;
}
if(!lim&&!zro&&fv[p][vis][sta]) return f[p][vis][sta];
int rig=lim?a[p]:9,ans=0;
int tv=vis,ts=sta;
for(int i=0;i<=rig;i++){
if(!zro||i) vis|=(1<<i),sta^=(1<<i);
ans+=dfs(p-1,lim&&i==rig,zro&&!i);
vis=tv,sta=ts;//回溯
}
if(!lim&&!zro) fv[p][vis][sta]=1,f[p][vis][sta]=ans;
return ans;
}
int solve(int x){
len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,1,1);
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>t;
while(t--){
cin>>l>>r;
cout<<solve(r)-solve(l-1)<<"\n";
}
return 0;
}
时间复杂度 \(O(T+3^B\times B\log_B N)\),诶为什么不是 \(4^B\) 呢?因为 \(vis_i=0,sta_i=1\) 是冗余状态,是根本不可能被搜到的~
所以我们完全可以用三进制将后两维替代掉。
空间从原来的 \(20\times 4^{10}=20971520\) 优化到了 \(20\times 3^{10}=1180980\),砍掉了将近 \(95\%\)。很震惊吧~
虽说理论时间复杂度没有优化,但是开数组的时间也随着一起优化了。我们会在本题的最后进行效率的对比。
点击查看代码 - R233820636
#include<bits/stdc++.h>
#define int unsigned long long
const int N=20;
using namespace std;
int t,l,r,len,a[N],sta[N],f[N][59049];//3^10=59049
bitset<59049> fv[N];
//0没访问,1访问奇数次,2访问偶数次
inline int to_num(){
int ans=0;
for(int i=0;i<=9;i++) ans=ans*3+sta[i];
return ans;
}
int dfs(int p,bool lim,bool zro){
if(!p){
for(int i=0;i<=9;i++) if(sta[i]&&(sta[i]&1)==(i&1)) return 0;
return 1;
}
int num=to_num();
if(!lim&&!zro&&fv[p][num]) return f[p][num];
int rig=lim?a[p]:9,ans=0;
for(int i=0,ts;i<=rig;i++){
ts=sta[i];
if(!zro||i) sta[i]=((sta[i]&1)?2:1);
ans+=dfs(p-1,lim&&i==rig,zro&&!i);
sta[i]=ts;//回溯
}
if(!lim&&!zro) fv[p][num]=1,f[p][num]=ans;
return ans;
}
int solve(int x){
len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,1,1);
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>t;
while(t--){
cin>>l>>r;
cout<<solve(r)-solve(l-1)<<"\n";
}
return 0;
}
在朴素做法的基础上,其实只要 pos、vis奇数位上1的个数、vis偶数位上1的个数、sta奇数位上1的个数、sta偶数位上1的个数 都分别相等,两个状态的答案就是一样的。
原理很好懂,比如你一共填写了 \(n\) 个奇数,其中有 \(m\) 个奇数出现了奇数次,那么你不需要关注这些数具体是几,因为这没有影响。比如说截至目前填写了 \(331132377\),那么我把 \(1\) 和 \(7\) 互换,或者把 \(3\) 都换成 \(9\)……都不会影响结果。偶数同理。
这样空间优化到了 \(20\times 6^4=25920\),时间复杂度也得到了大幅优化,优于洛谷上的题解。
点击查看代码 - R233825477
#include<bits/stdc++.h>
#define int unsigned long long
#define pc(x) __builtin_popcount(x)//x 二进制表示下 1 的个数
#define eve(x) pc((x)&341)//x偶数位上1的个数,原理:341 = 2^0 + 2^2 + 2^4 + 2^6 + 2^8
#define odd(x) pc((x)&682)//x奇数位上1的个数,原理:682 = 2^1 + 2^3 + 2^5 + 2^7 + 2^9
const int N=20;
using namespace std;
int t,l,r,len,a[N],vis,sta,f[N][1296];
bitset<1296> fv[N];
int dfs(int p,bool lim,bool zro){
if(!p){
for(int i=0;i<=9;i++) if(((vis>>i)&1)&&((sta>>i)&1)==(i&1)) return 0;
return 1;
}
int num=216*eve(vis)+36*odd(vis)+6*eve(sta)+odd(sta);//压成六进制数
if(!lim&&!zro&&fv[p][num]) return f[p][num];
int rig=lim?a[p]:9,ans=0;
int tv=vis,ts=sta;
for(int i=0;i<=rig;i++){
if(!zro||i) vis|=(1<<i),sta^=(1<<i);
ans+=dfs(p-1,lim&&i==rig,zro&&!i);
vis=tv,sta=ts;//回溯
}
if(!lim&&!zro) fv[p][num]=1,f[p][num]=ans;
return ans;
}
int solve(int x){
len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,1,1);
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>t;
while(t--){
cin>>l>>r;
cout<<solve(r)-solve(l-1)<<"\n";
}
return 0;
}
运行效率对比
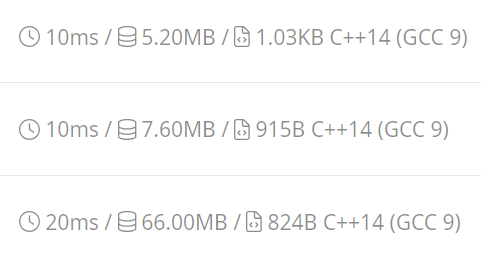
从下到上分别是三份代码的运行情况。
SPOJ 数据较少不易看出时间差距,因此我在本地进行了测试,测试数据 \(T=1000\),其他范围同题。
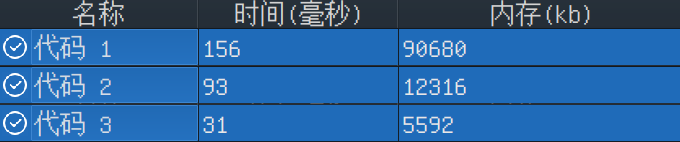
学到的:对数位 DP 来说,状态表示越简洁,DP 数组就越小巧,进而时空开销就越少。所以面对一道题,可以先打出暴搜,然后把所有上下文变量都扔进 \(f\) 数组里,在此基础上,考虑如下优化:
- 逐步思考哪些状态是一样的,进而优化维度或者每一维的大小。
最重要,优化上限也最高,是数位 dp 的精髓,可以同时优化时间和空间。- 搜索中途可能有一些状态需要剪枝。
优化时间,记忆化越强效果越不明显,但是应该作为写搜索的一个习惯。- 思考 dp 数组有没有冗余空间(根本搜索不到的那种)。
优化时空常数,可应对一些卡常的题。
CF1073E Segment Sum
之前的题不是求个数,就是求数位和,然而这道题让我们直接对满足条件的数求和。
由于 \(p+1\) 到最高位的填写情况不同,所以不能像 P4999 那样用 \(sum\) 来记忆化,否则状态数量太多了,跟直接暴搜没什么区别,而且还会炸空间。
根本原因在于我们的 \(sum\) 是自上往下计算的,也就是说当前状态的 \(sum\) 将更高位的贡献也统计进来了。把更高位的填写情况放到上下文里面,就导致了几乎不存在 \(sum\) 相同的两个状态。
为此,我们需要对 \(sum\) 进行修改,使其仅存储每个答案的前 \(p\) 位之和。我们也不再将 \(sum\) 作为参数传递,而是将其作为返回值。这样就做到了自下往上计算。
那么在递归树上,怎么根据子节点的 \(sum\) 来计算当前节点的 \(sum\) 呢?
我们额外记录一个 \(cnt\) 表示答案个数,那么对于状态 \(u\),若令 \(d[i]\) 为 \(pos\) 位填 \(i\) 得到的状态,则有:
可以结合下图来理解(右侧是最高位,箭头上的数字是 \(i \times 10^{pos-1}\))。
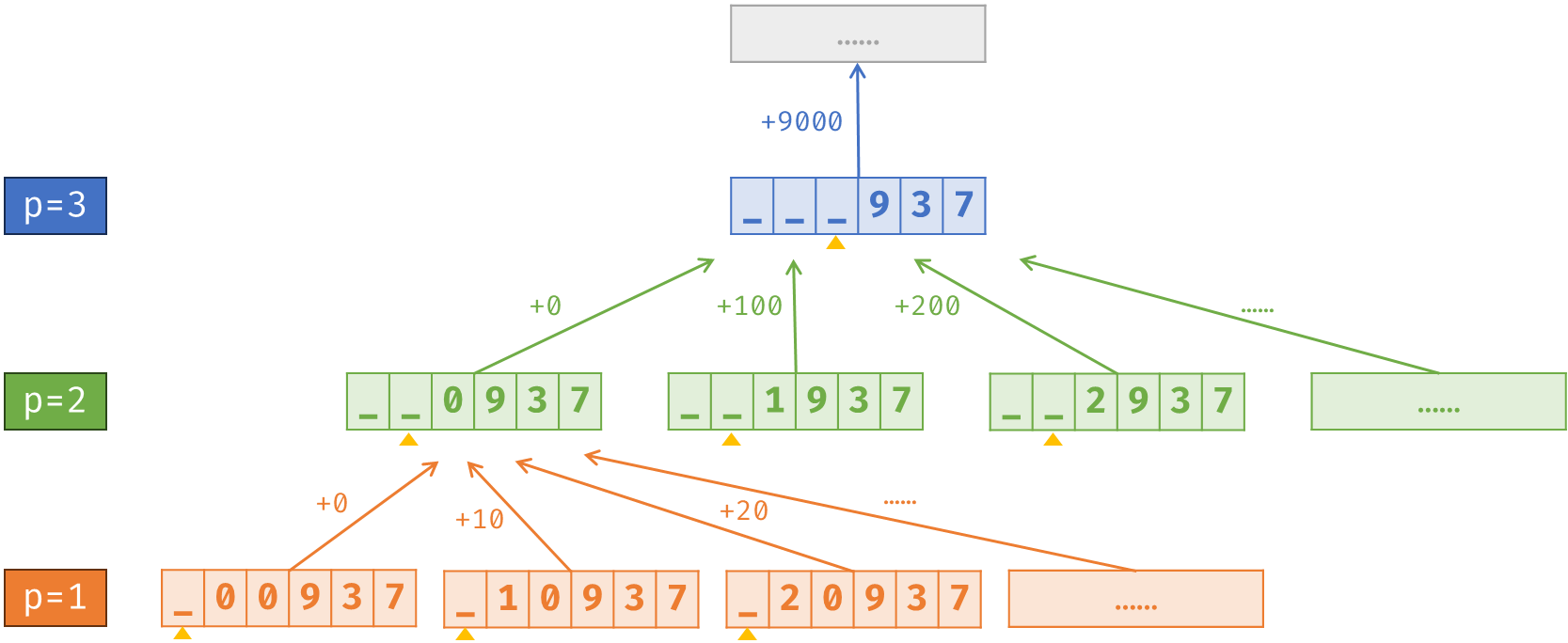
这样我们用 \(f[pos][vis]\) 来记忆化就没有问题了,其中 \(vis\) 是 \(0\sim 9\) 的访问情况压缩而成的整数。
点击查看代码 - #336251437
#include<bits/stdc++.h>
#define pc(x) __builtin_popcount(x)
#define int long long
#define PII pair<int,int>//(sum,cnt)
using namespace std;
const int N=20,P=998244353;
int l,r,k,len,a[N],vis,pw[N];
PII f[N][1024];
bitset<1024> fv[N];
PII dfs(int p,bool lim,bool zro){
if(pc(vis)>k) return {0,0};
if(!p) return {0,1};
if((lim^1)&(zro^1)&fv[p][vis]) return f[p][vis];
int rig=lim?a[p]:9,tv=vis;
PII t,ans{0,0};
for(int i=0;i<=rig;i++){
if(!zro||i) vis|=(1<<i);
t=dfs(p-1,lim&&i==rig,zro&&!i);
ans.first+=t.first+t.second*i*pw[p-1]%P;
ans.second+=t.second;
vis=tv;
}
ans.first%=P,ans.second%=P;
if((lim^1)&(zro^1)) fv[p][vis]=1,f[p][vis]=ans;
return ans;
}
int solve(int x){
len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,1,1).first;
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
pw[0]=1;
for(int i=1;i<N;i++) pw[i]=pw[i-1]*10%P;
cin>>l>>r>>k;
cout<<(solve(r)-solve(l-1)+P)%P<<"\n";
return 0;
}
学到的:自下向上统计答案。
再刷 P4999 烦人的数学作业
能否使用 CF1073E 中“自下向上统计答案”的方法来优化状态空间呢?
当然可以,只需要把上面式子中的 \(10^{pos-1}\) 去掉就行。
时间复杂度从 \(O(T+B^2\log_B N)\) 降到了 \(O(T+B\log N)\)。
点击查看代码 - R233900285
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=20,P=1e9+7;
int t,l,r,len,a[N];
bitset<N> fv;
struct Data{int sum,cnt;}f[N];
Data operator+(Data a,Data b){return {(a.sum+b.sum)%P,(a.cnt+b.cnt)%P};}
Data operator*(Data a,int b){return {b*a.sum%P,b*a.cnt%P};}
Data dfs(int p,bool lim){
if(!p) return {0,1};
if(!lim&&fv[p]) return f[p];
int rig=lim?a[p]:9;
Data ans{0,0};
for(int i=0;i<=rig;i++){
Data t=dfs(p-1,lim&&i==rig);
ans=ans+t,(ans.sum+=i*t.cnt)%=P;
}
if(!lim) fv[p]=1,f[p]=ans;
return ans;
}
inline int solve(int x){
len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,1).sum;
}
signed main(){
cin>>t;
while(t--){
cin>>l>>r;
cout<<(solve(r)-solve(l-1)+P)%P<<"\n";
}
return 0;
}
然后我们发现循环可以去掉,因为 \(i\in[0,rig)\) 时,得到的 \(t\) 都是相同的,所以直接将此区间内的贡献转化成 \(rig\times sum(t)+\frac{rig\times (rig-1)}{2}\times cnt(t)\) 就好;\(i=rig\) 时单独计算。
这样又省去了状态转移的 \(O(B)\),时间复杂度是严格的 \(O(T+\log_B N)\)。
点击查看代码 - R233900303
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=20,P=1e9+7;
int t,l,r,len,a[N];
bitset<N> fv;
struct Data{int sum,cnt;}f[N];
Data operator+(Data a,Data b){return {(a.sum+b.sum)%P,(a.cnt+b.cnt)%P};}
Data operator*(Data a,int b){return {b*a.sum%P,b*a.cnt%P};}
Data dfs(int p,bool lim){
if(!p) return {0,1};
if(!lim&&fv[p]) return f[p];
Data ans;
if(!lim){
ans=dfs(p-1,0)*10,(ans.sum+=dfs(p-1,0).cnt*45)%=P;
}else{
ans=dfs(p-1,0)*a[p];
(ans.sum+=dfs(p-1,0).cnt*(a[p]*(a[p]-1)/2))%=P;
Data t=dfs(p-1,1);
ans=ans+t,(ans.sum+=t.cnt*a[p])%=P;
}
if(!lim) fv[p]=1,f[p]=ans;
return ans;
}
inline int solve(int x){
len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,1).sum;
}
signed main(){
cin>>t;
while(t--){
cin>>l>>r;
cout<<(solve(r)-solve(l-1)+P)%P<<"\n";
}
return 0;
}
CF55D Beautiful Numbers
令 \(p+1\) 到最高位的内容为 \(num\),所填写数字的 \(\text{lcm}\) 值为 \(lcm\),则可以用 \(f[pos][num][lcm]\) 来记忆化,不过这样开销太大,光是 \(num\) 这一维就已经吃不消了,考虑优化。
如果令我们填过的数为 \(a_1,\dots,a_k\),则 \(num\equiv x\pmod{a_1,a_2,\dots,a_k}\) 的充要条件是 \(num\equiv x\pmod{\text{lcm}\{a_1,\dots,a_k\}}\)。
因此我们可以仅记录 \(num \bmod 2520\),而且 \(2520\) 是可选的最小的模数。这是因为对于所有 \(a\) 序列的选择,都满足 \(num\equiv x\pmod y \Longrightarrow num\equiv x\pmod{\text{lcm}\{a_1,\dots,a_k\}}\) 的 \(y\) 值,最小就是 \(2520\) 了。
然而这样还是会爆。不过我们发现 \(lcm\) 的取值个数其实就是 \(2520\) 的因数个数,只有 \(48\) 而已。所以我们将所有可能的 \(lcm\) 取值进行离散化。状态个数大约是 \(18\times 2520\times 48\),可以通过。
点击查看代码 - #336277615
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#define int long long
using namespace std;
using namespace __gnu_pbds;
const int N=20;
gp_hash_table<int,int> ma;
int t,l,r,len,a[N],f[N][2525][50];
inline int __lcm(int x,int y){return x/__gcd(x,y)*y;}
int dfs(int p,int num,int lcm,bool lim){
if(!p) return num%lcm==0;
int &g=f[p][num%2520][ma[lcm]];
if(!lim&&(~g)) return g;
int rig=lim?a[p]:9,ans=0;
for(int i=0;i<=rig;i++){
ans+=dfs(p-1,num*10+i,i?__lcm(lcm,i):lcm,lim&&i==rig);
}
if(!lim) g=ans;
return ans;
}
inline int solve(int x){
len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,0,1,1);
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
memset(f,-1,sizeof f);
for(int i=1,idx=0;i*i<=2520;i++) if(2520%i==0)
ma[i]=++idx,ma[2520/i]=++idx;
cin>>t;
while(t--){
cin>>l>>r;
cout<<solve(r)-solve(l-1)<<"\n";
}
return 0;
}
P4127 [AHOI2009] 同类分布
和 CF55D 很相似,不过 \(\text{lcm}\) 变成了 \(+\) 运算,所以我们无法像 CD55D 一样找到 \(2520\) 这样固定的模数。
不妨枚举这个模数,也即枚举数位和 \(sum\)。递归结束时若当前的数位和 \(cur\) 等于 \(sum\),并且原数 \(num\) 能被 \(sum\) 整除则返回 \(1\),否则返回 \(0\)。
记忆化数组 \(f[pos][num\bmod sum][cur]\),和 CF55D 类似。
时间复杂度 \(O(B\log_B N)\times O(B^3\log^2_B N)\times O(B)=O(B^5\log^3_B N)\),因为跑不满而且加了剪枝(见代码,1.84s \(\rightarrow\) 0.77s)所以能过。
点击查看代码 - R234028060
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=19;
ll l,r,f[N][163][163];//为 sum 开一维会 MLE
int a[N],len,sum;
inline ll dfs(int p,bool lim,int num,int cur){
if(cur+9*p<sum) return 0;//剪枝 1
if(!lim&&(~f[p][cur][num])) return f[p][cur][num];
if(!p) return cur==sum&&!num;
int rig=lim?a[p]:9;ll ans=0;
for(int i=0;i<=rig&&i+cur<=sum;i++)//剪枝 2
ans+=dfs(p-1,lim&&i==rig,(num*10+i)%sum,cur+i);
if(!lim) f[p][cur][num]=ans;
return ans;
}
inline ll solve(ll x){
len=0;
ll ans=0;
while(x) a[++len]=x%10,x/=10;
for(sum=1;sum<=9*len;sum++) memset(f,-1,sizeof f),ans+=dfs(len,1,0,0);
return ans;
}
signed main(){
cin>>l>>r;
cout<<solve(r)-solve(l-1)<<"\n";
return 0;
}
P3413 萌数
先打暴搜,参数有 \(pos,limit,zero\)。
可以选择额外添加一个 \(hui\) 表示到当前是否有回文。这样就可以剪一下枝 if(!limit&&hui) return pow10[pos],而且递归结束直接返回 hui 即可,无需循环判断。
接下来考虑如何记忆化,令填写情况为 \(sta\),我们发现当前的状态仅与 \(pos,sta[pos+1],sta[pos+2]\) 有关。在 \(pos\) 相同的情况下分类讨论:
- 后 \(2\) 位都不是前导 \(0\),而且都不一样。
- 后 \(2\) 位都不是前导 \(0\),而且都一样。
- 后 \(2\) 位中最高位是前导 \(0\)。
- 后 \(2\) 位都是前导 \(0\)。
我们又可以发现,\(2,3\) 两种情况本质是一样的,所以 \(pos\) 相同时最多只有 \(3\) 种答案。用 \(f[pos][stanum]\) 来记忆化,状态数为 \(1000\times 3\)。
注意此处我们记忆化的条件仅有 \(limit=0\),没有 \(zero\)。因为我们有意考虑了前导 \(0\) 的情况。
代码实现中,我们用 \(-1\) 表示 \(sta\) 数组中的前导 \(0\),这样就不需要 \(zero\) 参数了。
点击查看代码 - R233899166
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e3+10,P=1e9+7;
string l,r;
int a[N],len,sta[N],pw[N],f[N][3];
inline int check(string s){
int n=s.size();
for(int i=0;i<n-2;i++) if(s[i]==s[i+1]||s[i]==s[i+2]) return 1;
return s[n-2]==s[n-1];
}
int dfs(int p,bool hui,bool lim){
if(!lim&&hui) return pw[p];
if(!p) return hui;
int rig=lim?a[p]:9,ans=0,stanum;
stanum=((~sta[p+1])?(~sta[p+2])?0:1:2);
if(!lim&&(~f[p][stanum])) return f[p][stanum];
for(int i=0;i<=rig;i++){
sta[p]=(sta[p+1]==-1&&!i)?-1:i;
ans+=dfs(p-1,hui||(sta[p+1]==i)||(sta[p+2]==i),lim&&i==rig);
}
ans%=P;
if(!lim) f[p][stanum]=ans;
return ans;
}
inline int solve(string s){
len=s.size();
for(int i=1;i<=len;i++) a[i]=s[len-i]-'0';
sta[len+1]=sta[len+2]=-1;
return dfs(len,0,1);
}
signed main(){
memset(f,-1,sizeof f);
pw[0]=1;
for(int i=1;i<N;i++) pw[i]=pw[i-1]*10%P;
cin>>l>>r;
cout<<(solve(r)-solve(l)+check(l)+P)%P<<"\n";//沿用 CF628D 的技巧
return 0;
}
双倍经验:P6754 [BalticOI 2013] Palindrome-Free Numbers (Day1)
CF855E Salazar Slytherin's Locket
http://codeforces.com/problemset/problem/855/E
水蓝,压位到整数 \(sta\) 中统计每个值出现多少的奇偶性,注意处理前导 \(0\),最终 \(sta=0\) 说明全为偶数。
记忆化数组:\(f[b][pos][sta]\),其中 \(b\) 表示进制。
时间复杂度 \(O(2^B\times B\times N)\times O(B)+O(T)=O(T+2^B\times B^2\times N)\),其中 \(N\) 是位数。
容易发现,\(sta\) 也可以用 \(\text{popcount}(sta)\) 代替。
时间复杂度 \(O(B^2\times N)\times O(B)+O(T)=O(T+B^3\times N)\)。
两种写法均可通过,但后者更优。
上面复杂度是建立在为每一个 \(b\) 值都开一个 DP 数组从而无需清空的基础上。如果每个询问都清空,时间复杂度就是 \(O(T\times 2^B\times B\times N)\) 和 \(O(T\times B^2\times N)\)。
#1 - #336324490
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=62;
int q,b,l,r,a[N],len,sta,f[11][N][1024];
int dfs(int p,bool lim,bool zro){
if(!p) return !sta;
if(!lim&&!zro&&(~f[b][p][sta])) return f[b][p][sta];
int rig=lim?a[p]:b-1,ans=0,ts=sta;
for(int i=0;i<=rig;i++){
if(!zro||i) sta^=(1<<i);
ans+=dfs(p-1,lim&&i==rig,zro&&!i);
sta=ts;
}
if(!lim&&!zro) f[b][p][sta]=ans;
return ans;
}
inline int solve(int x){
len=0;
while(x) a[++len]=x%b,x/=b;
return dfs(len,1,1);
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
memset(f,-1,sizeof f);
cin>>q;
while(q--){
cin>>b>>l>>r;
cout<<solve(r)-solve(l-1)<<"\n";
}
return 0;
}
#2 - #336324647
#include<bits/stdc++.h>
#define pc(x) __builtin_popcount(x)
#define int long long
using namespace std;
const int N=62;
int q,b,l,r,a[N],len,sta,f[11][N][11];
int dfs(int p,bool lim,bool zro){
if(!p) return !sta;
int& g=f[b][p][pc(sta)];
if(!lim&&!zro&&(~g)) return g;
int rig=lim?a[p]:b-1,ans=0,ts=sta;
for(int i=0;i<=rig;i++){
if(!zro||i) sta^=(1<<i);
ans+=dfs(p-1,lim&&i==rig,zro&&!i);
sta=ts;
}
if(!lim&&!zro) g=ans;
return ans;
}
inline int solve(int x){
len=0;
while(x) a[++len]=x%b,x/=b;
return dfs(len,1,1);
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
memset(f,-1,sizeof f);
cin>>q;
while(q--){
cin>>b>>l>>r;
cout<<solve(r)-solve(l-1)<<"\n";
}
return 0;
}
P4124 [CQOI2016] 手机号码
先打暴搜,如果填到某一位同时存在 \(4,8\) 我们就直接返回 \(0\)。
接下来考虑记忆化。不难发现,只要下面的量相同,两个状态的答案就是相同的:
- 当前填到第几位。
- 是否填写过 \(4\)。
- 是否填写过 \(8\)。
- 当前位的前面第 \(1\) 位填写的是什么(如果不存在此位,视作 \(-1\))。
- 当前位的前面第 \(2\) 位填写的是什么(如果不存在此位,视作 \(-1\))。
- 是否出现过三连(即 \(3\) 个连续相同)。
都扔到 \(f\) 数组里即可。我为了图省事直接把所有数的填写状态压成一个 \(2^{11}\) 内的整数(不是 \(2^{10}\) 是因为包括 \(-1\))代替第 \(2,3\) 条扔进去了,状态数乘上转移,大概是 \(3\times 10^7\) 左右,是可以通过的(水死了
考虑优化。记 \(v_{i}\) 为我们填写的第 \(i\) 位,令不存在的位为 \(-1\)。
设 \(f_{pos,sta1,sta2}\) 为我们的记忆化数组,其中
- \(sta1\) 的取值和对应的情况:
- 未出现过三连:
- \(0\):\(v_{pos+1}=v_{pos+2}=-1\)
- \(1\):\(v_{pos+1}=v_{pos+2}\neq -1\)
- \(2\):\(\text{otherwise}\)
- \(3\):出现过三连
- 未出现过三连:
- \(sta2\) 的取值和对应情况:
- \(1\):填写过 \(4\) 或者 \(8\)
- \(0\):都没有填写过
显然,这样记忆化是正确的。代码中将它们压在一起了,状态数是 \(8\times n\)。
由于电话号码不能有前导 \(0\),搜索过程中,可以让最高位从 \(1\) 填起,效率会稍有提升。不过相应也需要注意主函数调用 solve(r)-solve(l-1) 时 \(l-1\) 可能变成 \(10\) 位数,此时 solve() 需要特判返回 \(0\)。
点击查看代码 - R233913577
#include<bits/stdc++.h>
#define int long long
const int N=12;
using namespace std;
int l,r,len,a[N],sta[N+2],vis,f[N][4][2];
int dfs(int p,bool is,bool lim,bool zro){
if(((vis>>4)&1)&&((vis>>8)&1)) return 0;
if(!p) return is;
int& g=f[p]
[is?3:(sta[p+1]==sta[p+2]?((~sta[p+1])?1:0):2)]
[((vis>>4)&1)||((vis>>8)&1)];
if(!lim&&!zro&&(~g)) return g;
int rig=lim?a[p]:9,ans=0,tv=vis;
for(int i=(p==len);i<=rig;i++){
bool tz=(zro&&!i);
if(tz) sta[p]=-1;
else sta[p]=i,vis|=(1<<i);
ans+=dfs(p-1,is||(i==sta[p+1]&&i==sta[p+2]),lim&&i==rig,tz);
vis=tv;
}
if(!lim&&!zro) g=ans;
return ans;
}
inline int solve(int x){
if(x<1e10) return 0;
len=0;
while(x) a[++len]=x%10,x/=10;
sta[len+1]=sta[len+2]=-1;
return dfs(len,0,1,1);
}
signed main(){
memset(f,-1,sizeof f);
cin>>l>>r;
cout<<solve(r)-solve(l-1)<<"\n";
return 0;
}
P2518 [HAOI2010] 计数
考虑在搜索的过程中记录所有数字的选择次数,然而状态数太多,难以优化。
实际上,只要 \(limit=0\),\(pos\) 及其之前的位置就可以随便填。
这就是一个多重集上的全排列问题。具体来说,记正在填写第 \(pos\) 位,\(limit=0\),数字 \(i\) 的剩余个数为 \(b_i\),则方案数为:
这样就完成了。
实现细节上,阶乘数量级过大,但是题目保证答案不超过 \(2^{63}-1\),所以我们不妨找一个 \(2^{63}-1\) 以上的质数 \(P\),计算模 \(P\) 意义下的答案,就可以使用逆元了,注意需要使用 __int128。
点击查看代码 - R234102036
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=52;
__int128 P,fact[N],inv[N];
int a[N],b[10],len;
string s;
__int128 qp(__int128 x,__int128 n){
__int128 a=1;
while(n){
if(n&1) a=a*x%P;
x=x*x%P,n>>=1;
}
return a;
}
inline ll calc(){
int x=0;__int128 y=1;
for(int i=0;i<=9;i++) x+=b[i],y=y*inv[b[i]]%P;
return fact[x]*y%P;
}
inline ll dfs(int p,bool lim){
if(!p) return 1;
if(!lim) return calc();
int rig=lim?a[p]:9;__int128 ans=0;
for(int i=0;i<=rig;i++){
if(!b[i]) continue;
b[i]--;
(ans+=dfs(p-1,lim&&i==rig))%=P;
b[i]++;
}
return ans;
}
inline ll solve(string s){
len=s.size();
memset(b,0,sizeof b);
for(int i=1;i<=len;i++) b[a[i]=s[len-i]-'0']++;
return dfs(len,1);
}
signed main(){
P=922337203ll;
P*=10000000000ll;
P+=6854775837ll;
fact[0]=fact[1]=1;
for(int i=2;i<N;i++) fact[i]=fact[i-1]*i%P;
inv[N-1]=qp(fact[N-1],P-2);
for(int i=N-1;i;i--) inv[i-1]=inv[i]*i%P;
cin>>s;
cout<<solve(s)-1<<"\n";
return 0;
}
另外一种方法,因为 \(N\le 50\) ,所以上式的质因数一定不超过 \(50\)。我们可以将 \(50\) 以内的质数打出来,将每个乘数 / 除数拆成质因数分解的形式再累加。代码可以参考此题解。
P2106 Sam 数
可以用 \(f[p][lst]\)(\(lst\) 为上一位填的值)来记忆化,然而第一维足足有 \(10^{18}\)。
这体现出了 DFS 写法相较递推写法的一个弊端:无法滚掉 \(p\) 这一维。
那么我们只好考虑递推怎么写。
然后就可以矩阵加速,只需构造转移矩阵:
时间复杂度 \(O(B^3\log K)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int B=10,P=1e9+7;
int k,f[B][B],bs[B][B],res[B][B],tmp[B][B],ans;
inline void mul(int res[B][B],int a[B][B],int b[B][B]){
memset(tmp,0,sizeof tmp);
for(int i=0;i<B;i++)
for(int j=0;j<B;j++)
for(int k=0;k<B;k++)
(tmp[i][j]+=a[i][k]*b[k][j])%=P;
memcpy(res,tmp,sizeof tmp);
}
inline void qp(int x){
for(int i=0;i<B;i++) res[i][i]=1;
while(x){
if(x&1) mul(res,res,bs);
mul(bs,bs,bs),x>>=1;
}
}
signed main(){
cin>>k;
for(int i=1;i<B;i++) f[0][i]=1;
for(int i=0;i<B;i++) for(int j=0;j<B;j++)
bs[i][j]=(abs(i-j)<=2);
qp(k-1),mul(f,f,res);
for(int i=0;i<B;i++) ans+=f[0][i];
cout<<ans%P+(k==1);//k=1时需要算入0
return 0;
}
学到的:在必要时使用递推写法。
P6371 [COCI 2006/2007 #6] V
\(K\) 较小的时候很显然可以开一维表示填过数位在模 \(K\) 下的值。
然而此题的 \(K\) 有 \(10^{11}\),怎么办呢?
我们发现,\(K\) 较大的时候,\(O(\dfrac{N}{K})\) 的暴力反而更优秀。
因此我们只需要选择一个分界点,来决定用哪种方法求解就好了。
这种技巧也称作——数据点分治!
这里选择分界点为 \(10^5\),两种做法的上限都在 \(10^8\) 以内(实测 \(10^3\) 更快,不过可能被卡)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define eb emplace_back
using namespace std;
const int N=15,mX=1e5+5,B=10;
int x,l,r,len,a[N],f[N][mX],tmp[N];
bitset<B> vis;
string s;
inline int dfs(int p,int s,bool lim,bool zro){
if(!p) return !s;
if(!lim&&!zro&&(~f[p][s])) return f[p][s];
int ans=0,rig=lim?a[p]:9;
for(int i=0;i<=rig;i++){
if(!vis[i]&&(i||(!i&&!zro))) continue;
tmp[p]=i;
ans+=dfs(p-1,(s*10+i)%x,lim&&i==a[p],zro&&!i);
}
if(!lim&&!zro) f[p][s]=ans;
return ans;
}
inline int solve(int x){
len=0;
while(x) a[++len]=x%10,x/=10;
return dfs(len,0,1,1);
}
inline bool check(int x){
string s=to_string(x);
for(char i:s) if(!vis[i-'0']) return 0;
return 1;
}
signed main(){
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
memset(f,-1,sizeof f);
cin>>x>>l>>r>>s;
for(char i:s) vis[i-'0']=1;
if(x<mX){
cout<<solve(r)-solve(l-1)<<"\n";
}else{
int ans=0;
for(int i=(l+x-1)/x*x;i<=r;i+=x) ans+=check(i);
cout<<ans<<"\n";
}
return 0;
}
学到的:使用数据点分治解决问题。
P14094 [ICPC 2023 Seoul R] Special Numbers
考虑使用 \(f[pos][g]\) 记忆化,其中:
- \(pos\) 表示当前填到第几位。
- \(g\) 表示填过位置的乘积与 \(k\) 的 \(\gcd\)。
根据这个表格我们知道,\(10^{17}\) 内的因数最多的数(即 Highly Composite Numbers,表格数据来源)只有不到 \(65536\) 个因数。所以 \(g\) 的取值不超过 \(65536\) 种,将第二维离散化一下就可以了。
代码中,第二位是用哈希表(gp_hash_table)现用现算的,常数不小,但是目前谷上最优解。
点击查看代码
#include<bits/stdc++.h>
#include<ext/pb_ds/assoc_container.hpp>
#include<ext/pb_ds/hash_policy.hpp>
#define int long long
using namespace std;
using namespace __gnu_pbds;
const int N=25,P=1e9+7;
int k,len,a[N],f[N][65536],idx;
string l,r;
gp_hash_table<int,int> ma;
inline int gcd(__int128 a,int b){
int r=a%b;
while(r) a=b,b=r,r=a%b;
return b;
}
inline int dfs(int p,__int128 fc,bool zro,bool lim){
int g=gcd(fc,k),gg;
if(!p) return g==k;
if(ma.find(g)==ma.end()) ma[g]=gg=idx++;
else gg=ma[g];
if(!zro&&!lim&&(~f[p][gg])) return f[p][gg];
int rig=lim?a[p]:9,ans=0;
for(int i=0;i<=rig;i++){
bool tzro=zro&&!i;
ans+=dfs(p-1,tzro?1:fc*i,tzro,lim&&i==rig);
}
ans%=P;
if(!zro&&!lim) f[p][gg]=ans;
return ans;
}
inline int solve(string& s){
len=s.size();
for(int i=0;i<len;i++) a[len-i]=s[i]-'0';
return dfs(len,1,1,1);
}
inline bool check(string& s){
int f=1;
for(int i:s) if(!((f*=i-'0')%=k)) return 1;
return 0;
}
signed main(){
memset(f,-1,sizeof f);
cin>>k>>l>>r;
cout<<(solve(r)-solve(l)+check(l)+P)%P<<"\n";
//字符串-1不好做,左端点单独处理(其实int128就可以)
return 0;
}
另一种做法是考虑到 \(k\) 若有某个超过 \(10\) 的质因数,则一定无解。因此只需要用质因子 \(2,3,5,7\) 的指数进行记忆化即可。
学到的:用离散化压缩空间规模。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号