[题解]P13586 [NWRRC 2023] First Solved, Last Coded

P13586 [NWRRC 2023] First Solved, Last Coded

参考题解：this by littleKtian。

我们令 \(f[i][j][len]\) 为 \(a,b\) 中，分别以 \(i\) 和 \(j\) 为左端点，长度为 \(len\) 的区间能否匹配。

我们可以枚举与 \(a[i]\) 在 \(b\) 中对应的位置 \(k\)，根据栈的性质，其他 \(a\) 中元素与 \(b\) 中元素的对应关系形如下图：

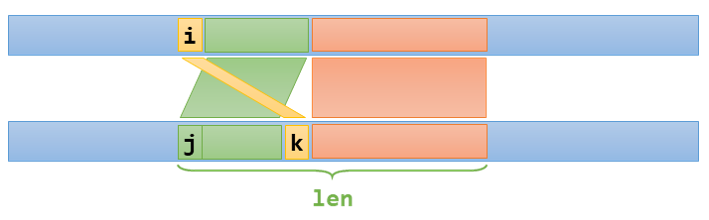
于是可以写出状态转移方程：

\[f[i][j][len]=\bigvee\limits_{k=j}^{j+len-1} [a[i]=b[k]]\land f[i+1][j][k-j]\land f[i+k-j+1][k+1][j+len-1-k] \]

按 \(len\) 从小到大是符合转移顺序的，不过记忆化搜索也可以。

输出方案可以额外使用一次搜索。

时间复杂度为 \(O(n^4)\)。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=101;
int n,a[N],b[N];
bitset<N> f[N][N],v[N][N];
bool dfs(int i,int j,int len){
	if(!len) return 1;
	if(v[i][j][len]) return f[i][j][len];
	for(int k=j;k<j+len;k++){
		f[i][j][len]=f[i][j][len]|((a[i]==b[k])&&dfs(i+1,j,k-j)&&dfs(i+k-j+1,k+1,j+len-1-k));
	}
	return v[i][j][len]=1,f[i][j][len];
}
void print(int i,int j,int len){
	if(!len) return;
	for(int k=j;k<j+len;k++){
		if((a[i]==b[k])&&dfs(i+1,j,k-j)&&dfs(i+k-j+1,k+1,j+len-1-k)){
			cout<<'S';
			print(i+1,j,k-j);
			cout<<'C';
			print(i+k-j+1,k+1,j+len-1-k);
			break;
		}
	}
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	for(int i=1;i<=n;i++) cin>>b[i];
	if(dfs(1,1,n)) cout<<"YES\n",print(1,1,n);
	else cout<<"NO\n";
	return 0;
}