[笔记]状压 DP

状压 DP 是动态规划的一种，通过将状态集合压缩成一个整数以实现状态转移的目的。

其中状态集合由若干个独立状态组成。很多情况下，每种独立状态都只有 \(2\) 种取值，也即二元状态。这种情况下，我么经常用 \(n\) 位二进制数来表示这 \(n\) 个二元状态组成的集合。

P1896 [SCOI2005] 互不侵犯

令 \(f[i][j][l]\) 为前 \(i\) 行，第 \(i\) 行的状态为 \(j\)，且已经放置 \(l\) 个国王的方案数。

这里的 \(j\) 就是状态集合压缩而成的整数。比如当前行的填写情况是（图片来源 OI Wiki）：

img

不妨令棋盘左端为二进制最低位，那么该状态对应的 \(j=100101_{(2)}=37\)。

显然每一种放置方法都能唯一地表示为这样一个整数。

考虑 \(i-1\) 行的状态 \(x\) 转移到状态 \(j\) 需要满足的条件。

  • \(x\) 不存在行内冲突。
  • \(j\) 不存在行内冲突。
  • \(x,j\) 两行之间不存在冲突。

前两个条件，状态 \(t\) 不存在行内冲突，当且仅当 (t&(t<<1))==0。我们可以预处理出所有这样的状态，然后改变 \(f\) 的含义，用 \(x,j\) 直接表示状态的编号。

第三个条件，其实就是要同时满足：

  • (x&j)==0
  • (x&(j<<1))==0
  • ((x<<1)&j)==0

对于每个满足条件的 \(x\)，我们再枚举 \(l\) 来转移就可以了。

时间复杂度似乎是 \(O(n\times 2^n\times 2^n\times k)\)？

实际上不难发现，剔除行内冲突的状态后，剩余的状态个数，即为长度为 \(n\) 的 \(01\) 串中，任两个 \(1\) 不相邻的方案数。

这个方案数是 \(\text{Fib}(n+2)\)，即斐波那契数列的第 \(n+2\) 项。理解起来很容易，我们令 \(g[i]\) 为填写到第 \(i\) 位的方案数，则有 \(g[i]=g[i-1]+g[i-2]\)（对应着第 \(i\) 位填 \(0/1\)），与斐波那契数列的递推式一致。

所以更准确的时间复杂度为 \(O(n\times \text{Fib}^2(n)\times k)=O(n^3\times\text{Fib}^2(n))\)，其中 \(\text{Fib}(n)\) 也可以替换为同阶的 \(\varphi ^n\approx 1.618^n\)。

点击查看代码 - R232968409 
#include<bits/stdc++.h>
#define int long long
#define pc(x) __builtin_popcount(x)//x 在二进制表示下有多少个 1
using namespace std;
const int N=9;
int n,k,sta[1<<N],cnt[1<<N],idx,f[N][1<<N][N*N],ans;
inline bool valid(int x,int y){
	if(x&y) return 0;
	if(x&(y<<1)) return 0;
	if((x<<1)&y) return 0;
	return 1;
}
signed main(){
	cin>>n>>k;
	for(int i=0,lim=(1<<n)-1;i<=lim;i++) if(!(i&(i<<1))){
		sta[idx]=i,f[0][idx][cnt[idx++]=pc(i)]=1;
	}
	for(int i=1;i<n;i++){
		for(int j=0;j<idx;j++){//当前行的状态
			for(int x=0;x<idx;x++){//上一行的状态
				if(valid(sta[j],sta[x])^1) continue;
				for(int l=cnt[j];l<=k;l++){
					f[i][j][l]+=f[i-1][x][l-cnt[j]];
				}
			}
		}
	}
	for(int i=0;i<idx;i++) ans+=f[n-1][i][k];
	cout<<ans<<"\n";
	return 0;
}

P1879 [USACO06NOV] Corn Fields G

上题弱化版，一是不需要限制放多少棋子，二是互相攻击的条件从八连通变成四连通。

时间复杂度 \(O(m\times\text{Fib}^2(n))\)。

下面给出代码。

点击查看代码 - R232967816 
#include<bits/stdc++.h>
#define pc(x) __builtin_popcount(x)
using namespace std;
const int M=12,N=12,P=1e8;
int m,n,idx,a[M],f[M][1<<N],sta[1<<N];
long long ans;
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>m>>n;
	for(int i=0;i<m;i++)
		for(int j=0,x;j<n;j++)
			cin>>x,a[i]|=((x^1)<<j);
	for(int i=0,lim=(1<<n);i!=lim;i++){
		if(i&(i>>1)) continue;
		sta[idx]=i;
		if(!(i&a[0])) f[0][idx]=1;
		idx++;
	}
	for(int i=1;i<m;i++){
		for(int j=0;j<idx;j++){
			if(sta[j]&a[i]) continue;
			for(int k=0;k<idx;k++){
				if(i>1&&(sta[k]&a[i-1])) continue;
				if(sta[j]&sta[k]) continue;
				(f[i][j]+=f[i-1][k])%=P;
			}
		}
	}
	for(int i=0;i<idx;i++) ans+=f[m-1][i];
	cout<<ans%P<<"\n";
	return 0;
}

P2704 [NOI2001] 炮兵阵地

与 P1896 类似，只是判定范围有所不同。

这道题我们需要记录前 \(2\) 行的状态，即用 \(f[i][j][k]\) 表示前 \(i\) 行，第 \(i\) 行状态为 \(j\)，第 \(i-1\) 行状态为 \(k\) 的最大数量。

\(f[i][j][k]\) 可以由 \(f[i-1][k][l]\) 转移而来，我们仅需枚举这样的 \(l\)，判断 \(j,k,l\) 三个连续行的状态是否合法，若合法则转移。

为了提升效率，我们仍然将行内冲突的状态剔除掉。

时间复杂度不好衡量，如果令剔除后的状态数是 \(k\) 的话（经测试 \(k\) 的上界是 \(60\)），时间复杂度应为 \(O(nm+2^m+k^3n)\)。

点击查看代码 - R232968551 
#include<bits/stdc++.h>
#define pc(x) __builtin_popcount(x)
using namespace std;
const int N=100,M=10;
int n,m,lim,idx,a[N],f[N][1<<M][1<<M],sta[1<<M],cnt[1<<M],ans;
string s;
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=0;i<n;i++){
		cin>>s;
		for(int j=0;j<m;j++) a[i]|=((s[j]=='H')<<j);
	}
	for(int i=0,lim=(1<<m);i<lim;i++){
		if((i&(i<<1))||(i&(i<<2))) continue;
		sta[idx]=i,cnt[idx]=pc(i);
		if(!(i&a[0])) f[0][idx][0]=pc(i);
		idx++;
	}
	for(int i=1;i<n;i++){
		for(int j=0;j<idx;j++){//第 i 行的状态
			if(sta[j]&a[i]) continue;
			for(int k=0;k<idx;k++){//第 i-1 行的状态
				if(sta[k]&a[i-1]) continue;
				if(sta[j]&sta[k]) continue;
				for(int l=0;l<idx;l++){//第 i-2 行的状态
					if(i>1&&(sta[l]&a[i-2])) continue;
					if(sta[j]&sta[l]) continue;
					if(sta[k]&sta[l]) continue;
					f[i][j][k]=max(f[i][j][k],f[i-1][k][l]+cnt[j]);
				}
			}
		}
	}
	for(int i=0;i<idx;i++){
		for(int j=0;j<idx;j++){
			ans=max(ans,f[n-1][i][j]);
		}
	}
	cout<<ans<<"\n";
	return 0;
}

P8756 [蓝桥杯 2021 省 AB2] 国际象棋

与 P2704 类似地，需要记录 \(i,i-1\) 共两行的状态。

又与 P1856 类似，需要额外开一维限制“已经放了 \(x\) 个棋子”。

所以 DP 数组一共 \(4\) 维，具体见代码。

因为同一行无论怎么放内部都是合法的，所以无法缩减状态规模。时间复杂度为 \(O(m\times 2^{3n})\)。

点击查看代码 - R232960233 
#include<bits/stdc++.h>
#define pc(x) __builtin_popcount(x)
using namespace std;
const int N=6,M=100,K=21,P=1e9+7;
int n,m,lim,kk,f[M][1<<N][1<<N][K];
long long ans;
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>m>>kk;
	lim=(1<<n);
	for(int i=0;i<lim;i++) f[0][i][0][pc(i)]=1;
	for(int i=1;i<m;i++){
		for(int j=0;j<lim;j++){
			for(int k=0;k<lim;k++){
				if(((j>>2)&k)|((k>>2)&j)) continue;
				for(int l=0;l<lim;l++){
					if(((l>>2)&k)|((k>>2)&l)) continue;
					if(((l>>1)&j)|((j>>1)&l)) continue;
					for(int o=pc(j);o<=kk;o++){
						(f[i][j][k][o]+=f[i-1][k][l][o-pc(j)])%=P;
					}
				}
			}
		}
	}
	for(int i=0;i<lim;i++){
		for(int j=0;j<lim;j++){
			ans+=f[m-1][i][j][kk];
		}
	}
	cout<<ans%P<<"\n";
	return 0;
}

P5911 [POI 2004] PRZ

令 \(S\) 为原集合的一个子集，\(f[S]\) 为 \(S\) 过桥所花的最短时间，\(w[S],t[S]\) 分别表示 \(S\) 内元素的重量之和，最长时间。

则有转移：

\[f[S]=\min\limits_{T\subseteq S,w[\complement_S T]\le W} f[T]+t[\complement_S T] \]

每一个子集同样可以表示为一个 \(n\) 位二进制数，第 \(i\) 位为 \(1\) 表示第 \(i\) 个元素被选入子集。

然后就可以按式子进行递推了。

\(T\subseteq S\) 即 T&S==T。不过遍历 \(S\) 已经是 \(O(2^n)\) 的，如果遍历 \(T\) 仍然是 \(O(2^n)\) 的话，总时间将达到 \(O(2^{2n})\)，不可接受。

实际上，我们可以做到直接枚举 \(S\) 的每一个子集，仅需像下面这样写：

for(S=0;S<(1<<n);S++){
	for(T=S;T;T=(T-1)&S){
        //...
	}
}

正确性不难理解，主要对时间复杂度 \(O(3^n)\) 进行证明。

\(\bf{Proof:}\)
对于一个 \(S\)，若它的二进制表示有 \(k\) 个 \(1\)，则它的子集数量为 \(2^k\)。而有 \(k\) 个 \(1\) 的集合 \(S\) 有 \(C_n^k\) 种，于是所有子集的总数是：

\[\sum\limits_{k=0}^n C_n^k\times 2^k \]

根据二项式定理，这是 \((1+2)^n\) 的展开形式，所以子集总数是 \(3^n\)。

另外注意枚举 \(S\) 的顺序，\(T\) 转移到 \(S\) 时必须保证 \(f[T]\) 已经被计算好，从小到大遍历 \(S\) 就能做到这一点。

时间复杂度 \(O(3^n)\)。

点击查看代码 - R232902835 
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=16;
int W,n,lim,f[1<<N],tt[1<<N],ww[1<<N];
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>W>>n;
	lim=(1<<n);
	for(int i=0,t,w;i<n;i++){
		cin>>t>>w;
		for(int j=0;j<lim;j++){
			if((j>>i)&1) tt[j]=max(tt[j],t),ww[j]+=w;
		}
	}
	memset(f,0x3f,sizeof f);
	for(int i=0;i<lim;i++){//S
		if(ww[i]<=W) f[i]=tt[i];
		for(int j=i;j;j=(j-1)&i){//T
			if(ww[i^j]<=W){//i^j 即 T 在 S 中的补集
				f[i]=min(f[i],f[j]+tt[i^j]);
			}
		}
	}
	cout<<f[lim-1]<<"\n";
	return 0;
}

P4363 [九省联考 2018] 一双木棋 chess

这道题我们不能以某一行的选择情况为状态，因为这样转移会有后效性。因此我们需要想办法把整个棋盘的摆放情况记录下来。

压缩到一个 \(2^{n\times m}\) 的整数？这样空间就爆了。

不过题目有限制，所放置的位置上方和左方必须放置棋子。

也就是说，任何时刻棋盘上的棋子，都构成一个左上方的阶梯形。

这种情况下，有一个常用的技巧。将状态用 \(m\) 个 \(0\) 和 \(n\) 个 \(1\) 来表示。具体来说，用 \(1\) 表示棋子，每个 \(1\) 更低位 \(0\) 的个数表示该棋子所在行有多少个棋子。下图是一个例子：

img

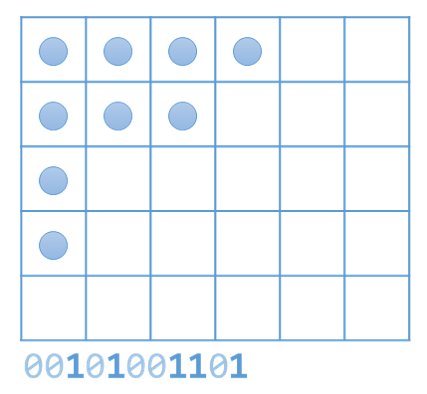
其实还有另一种理解方式，从 \((n,0)\) 开始，根据状态码移动，\(0\) 是向右，\(1\) 是向上，最终一定会走到 \((0,m)\)，而经过的位置恰好是这个阶梯形的轮廓线：

img

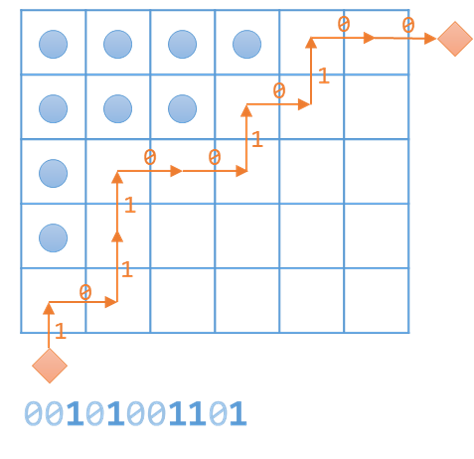
因此，这种状压 DP 也被称作轮廓线 DP。

总之我们的状态数是优化到了 \(C_{n+m}^n\)。

转移过程不难理解，就是找当前状态码中的一段 01，将其变成 10，就相当于在这段 01 的拐角处放置了一颗棋子。至于拐角位置在哪，我们只需按上图的规则，在遍历过程中逐格移动即可找到。

状态数是 \(C_{n+m}^n\)，再乘上转移的 \(O(n+m)\)，总时间复杂度是 \(O(C_{n+m}^n\times (n+m))\)。

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int N=10,M=10,inf=1e9;
int n,m,a[N][M],b[N][M],f[1<<(N+M)],nul;
bitset<1<<(N+M)> vis;
int dfs(int sta,bool cur){//cur=1为黑 0为白 
	if(vis[sta]) return f[sta];
	f[sta]=cur?-inf:inf;
	int x=n,y=0;
	for(int i=0;i<n+m-1;i++){
		(sta>>i&1)?x--:y++;//跟着状态码移动
		if((sta>>i&3)!=1) continue;//是否遇到连续的 01
		if(cur){
			f[sta]=max(f[sta],dfs(sta^(3<<i),cur^1)+a[x][y]);//sta^(3<<i) 实现了 01 变成 10 的步骤
		}else{
			f[sta]=min(f[sta],dfs(sta^(3<<i),cur^1)-b[x][y]);
		}
	}
	return vis[sta]=1,f[sta];
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0); 
	cin>>n>>m;
	for(int i=0;i<n;i++) for(int j=0;j<m;j++) cin>>a[i][j];
	for(int i=0;i<n;i++) for(int j=0;j<m;j++) cin>>b[i][j];
	nul=f[0],vis[((1<<n)-1)<<m]=1;
	cout<<dfs((1<<n)-1,1)<<"\n";
	return 0;
}
posted @ 2025-08-24 23:12  Sinktank  阅读(59)  评论(0)    收藏  举报
★CLICK FOR MORE INFO★ TOP-BOTTOM-THEME
Enable/Disable Transition
Copyright © 2023 ~ 2025 Sinktank - 1328312655@qq.com
Illustration from 稲葉曇『リレイアウター/Relayouter/中继输出者』,by ぬくぬくにぎりめし.