[题解]P3200 [HNOI2009] 有趣的数列

P3200 [HNOI2009] 有趣的数列

给出另一种转化思路，模拟赛的时候想到的。

将我们构造的序列看作 \(n\) 个点 \((a_1,a_2),(a_3,a_4),\dots,(a_{2n-1},a_{2n})\)。

题目的限制条件转化为：

• \(a_i\) 构成 \(1,2,\dots,2n\) 的一个排列。
• 点 \(i\) 在 点 \(i-1\)的右上方。
• 所有点在直线 \(y=x\) 上方。

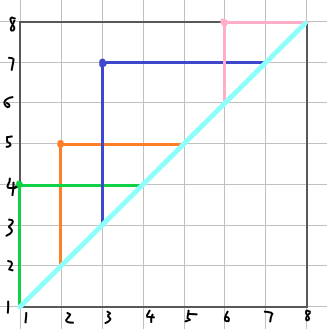
我们从这些点出发，作平行于 \(x,y\) 轴的直线，与图中的青色线段各交于一点。

条件 \(1\) 转化为这些点恰好覆盖整个青色线段上的 \(2n\) 个点。

条件 \(2\) 转化为青色线段上的同色区间没有嵌套关系。也就是说如果将这些区间按左端点排序，那么右端点构成的序列是单增的。

---

抛去网格，我们相当于为青色线段上的 \(2n\) 个点染 \(n\) 种颜色，每种颜色恰染 \(2\) 个点。

为了满足条件 \(2\)，我们仅需对 \(n\) 个左端点染色。这是因为根据上面的分析，剩下 \(n\) 个空位作为右端点，其颜色是确定的。

为了使区间合法，我们需要使得任意长度为 \(i\) 的前缀，左端点数量 \(\ge\) 右端点数量。

这样就完成了转化，所求答案即为第 \(n\) 个 Catalan 数。

回顾求 Catalan 数的方法。

• \(\large f_n=\sum\limits_{i=0}^{n-1} f_i f_{n-i-1}\)。必须 \(O(n^2)\) 递推，遂放弃。

• \(\large f_n=\frac{4n-2}{n+1} f_{n-1}\)。\(p\) 与 \(n+1\) 未必互质，无法求逆元；分式也未必是整数，不能化简，遂放弃。

• \(\large f_n=\frac{C_{2n}^n}{n+1}=\frac{\prod\limits_{i=n+2}^{2n} i}{\prod\limits_{i=1}^n i}\)。由于该分式的值一定是整数，我们就可以对每个 \(i\) 进行质因数分解，从而达到约分的效果。

  具体来说，我们仅需在欧拉筛的过程中记录 \(i\) 的最小质因数 \(mn_i\)。从大到小遍历每一个 \(i\)，并将 \(i\) 的指数分配给 \(mn_i\) 和 \(\frac{i}{mn_i}\)。直到只有质数剩余为止。

时间复杂度 \(O(n\log n)\)。

点击查看代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
int n,mod,a[2*N],mn[2*N],p[N],idx,ans=1;
int qp(int a,int n){
	int f=1;
	while(n){
		if(n&1) f=f*a%mod;
		a=a*a%mod,n>>=1;
	}
	return f;
}
void init(int n){
	for(int i=2;i<=n;i++){
		if(!mn[i]) p[++idx]=mn[i]=i;
		for(int j=1;j<=idx&&p[j]*i<=n;j++){
			mn[i*p[j]]=p[j];
			if(i%p[j]==0) break;
		}
	}
}
signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>n>>mod;
	init(2*n);
	for(int i=1;i<=n;i++) a[i]=-1;
	for(int i=n+2;i<=2*n;i++) a[i]=1;
	for(int i=2*n;i>1;i--) if(mn[i]!=i) a[mn[i]]+=a[i],a[i/mn[i]]+=a[i];
	for(int i=2;i<=2*n;i++) if(mn[i]==i) ans=ans*qp(i,a[i])%mod;
	cout<<ans<<"\n";
	return 0;
}