[题解]AtCoder Beginner Contest 413(ABC413) A~G
A - Content Too Large
输出Yes\(\iff \sum a_i\le m\)。
时间复杂度\(O(n)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m;
signed main(){
cin>>n>>m;
for(int i=1,x;i<=n;i++) cin>>x,m-=x;
cout<<(m<0?"No\n":"Yes\n");
return 0;
}
B - cat 2
枚举\(i,j\),扔到set里面统计即可。
时间复杂度\(O(n^2\log(n^2))=O(n^2\log n)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=105;
int n;
string s[N];
set<string> se;
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>s[i];
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i!=j) se.insert(s[i]+s[j]);
}
}
cout<<se.size();
return 0;
}
C - Large Queue
操作\(1\),将输入的\((c,x)\)作为一个整体,压入队列。
操作\(2\),不断出队列,直到\(k\)为\(0\)为止。若最后一个出队列的元素还没用完,再把剩下的从队头压入回队列。
因为出入栈次数上界都是\(2q\),所以时间复杂度为\(O(q)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int Q=2e5+10;
int n;
deque<pair<int,int>> q;
signed main(){
cin>>n;
int op,c,x;
while(n--){
cin>>op;
if(op==1){
cin>>c>>x;
q.push_back({c,x});
}else{
int ans=0;
cin>>c;
while(!q.empty()){
auto t=q.front();
q.pop_front();
if(c<t.first){
ans+=c*t.second;
q.push_front({t.first-c,t.second});
break;
}
c-=t.first;
ans+=t.first*t.second;
}
cout<<ans<<"\n";
}
}
return 0;
}
D - Make Geometric Sequence
下文中\(r\)表示公比。
对于\(|r|<1\),我们可以通过将序列翻转来让\(|r|\ge 1\)。
因此仅需判断是否存在这样的\(|r|\ge 1\)即可。
所以我们仅需将\(a\)按绝对值从小到大排序,看相邻元素是否都满足:
即:
然而我们发现\(r=-1\)的情况下,排序得到的\(a\)会有不同的形态。此时需要特判一下,即:
- 若将满足\(a[i]=a[1]\)的\(i\)的个数记为\(x\),\(a[i]=-a[i]\)的\(i\)的个数记为\(y\),则有\(x+y=n\)且\(|x-y|\le 1\)。
时间复杂度\(O(n\log n)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+10;
int t,n,a[N];
bool solve(){
cin>>n;
int c1=0,c2=0;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++)
if(a[i]==a[1]) c1++;
else if(a[i]==-a[1]) c2++;
if(c1+c2==n&&abs(c1-c2)<2) return 1;
sort(a+1,a+1+n,[](int a,int b){return abs(a)<abs(b);});
for(int i=2;i<n;i++)
if(a[i]*a[i]!=a[i-1]*a[i+1]) return 0;
return 1;
}
signed main(){
cin>>t;
while(t--) cout<<(solve()?"Yes\n":"No\n");
return 0;
}
E - Reverse 2^i
转化一下题意,相当于一棵完全二叉树,叶子节点存储的是\(a_1,a_2,\dots,a_{2^n}\)。可以任意次交换某个节点的左右子树。最后要使得叶子结点的字典序最小。
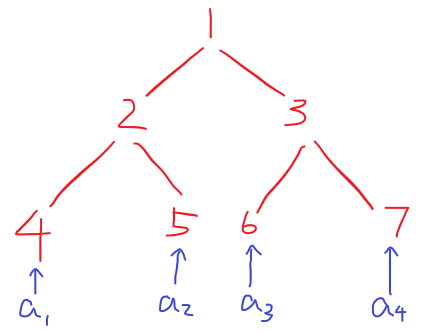
那么就有一个显然的贪心思路:每个节点仅需让左右子树中,\(\min\)值较小的那个作为左子树。
因为满足最优子结构所以正确性可以保证。
时间复杂度\(O(2^n)\)。
点击查看代码
#include<bits/stdc++.h>
const int N=(1<<18)+10;
using namespace std;
int t,n,nn,f[N<<1],l[N],r[N];
void dfs(int x){
if(x<nn) dfs(l[x]),dfs(r[x]);
else cout<<f[x]<<" ";
}
signed main(){
cin>>t;
while(t--){
cin>>n;
nn=(1<<n);
for(int i=0;i<nn;i++) cin>>f[nn+i];
for(int i=nn-1;~i;i--){
f[i]=min(f[l[i]=(i<<1)],f[r[i]=(i<<1|1)]);
if(f[l[i]]>f[r[i]]) swap(l[i],r[i]);
}
dfs(1);
cout<<"\n";
}
return 0;
}
F - No Passage
若没有Aoki的限制,我们使用BFS跑一遍最短路就可以。
加上限制之后,我们定义\(d[i][j]\)表示从\((i,j)\)开始,在Aoki的限制之下到达目标格子的最少步数。
Aoki为了让\((i,j)\)步数最大,一定会把周围\(d\)值最小的方向禁用掉。
因此\(d[i][j]\)仅能从周围次小的\(d\)值进行转移。
时间复杂度\(O(nm)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e3+10,M=3e3+10;
int n,m,k,d[N][M],dx[4]{-1,0,1,0},dy[4]{0,1,0,-1},ans;
queue<pair<int,int>> q;
int sec(int x,int y){
vector<int> v={d[x][y-1],d[x][y+1],d[x-1][y],d[x+1][y]};
sort(v.begin(),v.end());
return v[1];
}
signed main(){
memset(d,0x3f,sizeof d);
cin>>n>>m>>k;
for(int i=1,x,y;i<=k;i++){
cin>>x>>y;
d[x][y]=0;
q.push({x,y});
}
while(!q.empty()){
auto t=q.front();
q.pop();
int x=t.first,y=t.second;
for(int i=0;i<4;i++){
int xx=x+dx[i],yy=y+dy[i];
if(xx<1||xx>n||yy<1||yy>m) continue;
int td=sec(xx,yy);
if(td+1<d[xx][yy]){
d[xx][yy]=td+1;
q.push({xx,yy});
}
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(d[i][j]!=d[0][0]){
ans+=d[i][j];
}
}
}
cout<<ans<<"\n";
return 0;
}
G - Big Banned Grid
\((1,1)\)走不到\((n,m)\),当且仅当存在一个障碍物组成的八连通分量,使得它同时连接左/下边缘和右/上边缘。
八连通即通过八个方向可以走到。
时间复杂度\(O(k\log k)\)。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,m,k;
vector<int> lef,bot;
set<pair<int,int>> se;
int dx[8]{-1,-1,0,1,1,1,0,-1},dy[8]{0,1,1,1,0,-1,-1,-1};
bool dfs(int x,int y){
if(se.find({x,y})==se.end()) return 0;
se.erase({x,y});
if(x==1||y==m) return 1;
for(int i=0;i<8;i++){
int xx=x+dx[i],yy=y+dy[i];
if(xx<1||xx>n||yy<1||yy>m) continue;
if(dfs(xx,yy)) return 1;
}
return 0;
}
signed main(){
cin>>n>>m>>k;
for(int i=1,x,y;i<=k;i++){
cin>>x>>y;
se.insert({x,y});
if(x==n) bot.push_back(y);
if(y==1) lef.push_back(x);
}
for(int i:bot) if(dfs(n,i)) cout<<"No\n",exit(0);
for(int i:lef) if(dfs(i,1)) cout<<"No\n",exit(0);
cout<<"Yes\n";
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号